考虑齿侧间隙的两栖无人机变形机构动态特性分析

张华，宋梅利，刘永，刘治渝，沈敏

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

随着无人机技术的发展，多栖无人机在侦查探测、播种施肥等方面发挥着越来越重要的作用，受到世界各国的广泛关注[1]。摆臂变形机构能够很好地实现无人机两栖变形功能，也是无人机的关键部件之一。摆臂由行星传动结构组成，在旋转过程中，其传动精度和平稳性受到齿轮装配和制造误差影响，且影响过程比较复杂。所以研究摆臂变形机构的动态特性是非常重要的。为了防止齿轮卡死和存储润滑油，齿轮啮合副之间会存在一定侧隙。不合理的齿轮侧隙在啮合运转时会反复出现接触、脱离、再接触的冲击振动，影响摆臂变形机构的稳定性和旋转精度,进而影响无人机的工作性能。

近年来，国内外对于齿侧间隙进行了多方面研究，杜英杰[2]基于某弹翼展开机构，建立弹翼展开机构间隙接触碰撞的数学模型，并利用ADAMS仿真软件，研究了不同间隙大小、数量和材料对机构展开过程的动态特性影响；王凯达[3]研究了不同轴承间隙和齿面磨损对齿轮系统的影响，通过实验仿真得到不同状态下机构的动力学特性；TSAI S J等[4]为解决行星齿轮传动中多载荷接触齿对的静态不确定问题，讨论了变形的影响、分担载荷的变化、接触应力以及载荷传递误差；吴启豪等[5]探究齿侧间隙对船用人字齿轮动态特性的影响，在ADAMS中建立动态模型，比较不同齿侧间隙、不同运动状态下人字齿轮的运动状态，为人字齿轮优化设计提供了参考依据。目前行星轮系作为多栖无人机变形部件，其研究较少，轮系间各种误差因素会影响多栖无人机变形效果和运动性能。所以本文以摆臂变形机构为研究对象,结合ADAMS软件，建立了含齿轮侧隙的动态仿真模型,分析摆臂机构变形过程中不同侧隙大小、数目和材料等因素对机构动态特性的影响,并为下一步的结构优化提供参考。

1 摆臂变形机构工作原理

如图1所示，摆臂变形机构主要由轴1、轴2和轴3三个轴系部件组成。其中齿轮1为太阳轮，齿轮2为行星轮，旋转支撑臂为行星架；轴2与轴3通过锥齿轮传递运动。飞行状态时，轮桨部件与地面平行，桨叶呈水平状态；变形时，行星轮2既自转又公转，自转通过锥齿轮传动使轮桨部件由水平状态变为竖直状态，公转使行星轮围绕太阳轮进行旋转，轮桨部件位置发生改变，实现无人机由飞行模式到陆地模式的转换，如图2所示。

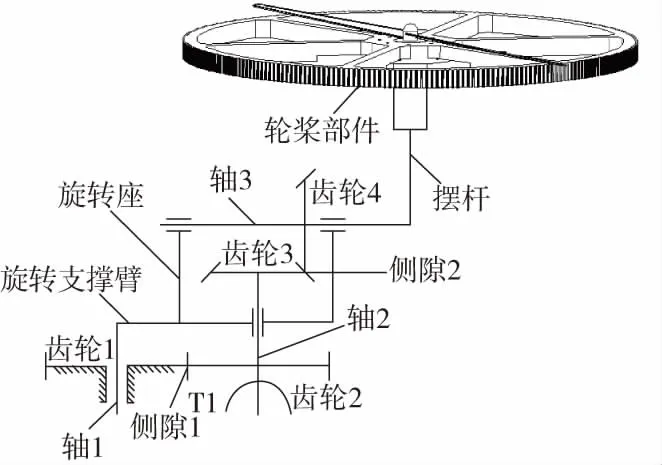
图1 摆臂变形机构简图

图2 两栖无人机陆空模式的转换

摆臂变形机构性能指标要求为：

1)摆臂能够迅速旋转到位，展开时间<1 s；

2)为了减小摆臂运转过程中的动载荷，摆杆角加速度峰值应<1×105m/s2；

3)当摆臂变形机构带动轮桨部件完成变形时，轴2和轴3同步误差<1°。

2 考虑齿侧间隙的摆臂变形机构理论模型

2.1 齿轮侧隙的计算

侧隙是指两个相配齿轮的工作面相接触时，在两个非工作面之间所形成的间隙。计算齿轮副的最小法向侧隙jnmin时，主要考虑齿轮副的热变形和润滑状况的工作条件[6]。其计算公式如下：

jnmin=2a(α1Δt1-α2Δt2)sinα′n+δmn

(1)

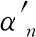
计算齿轮副的最大法向侧隙jnmax时，主要考虑齿轮的加工精度。其计算公式如下：

(2)

式中：Ts1、Ts2为小齿轮、大齿轮的齿厚公差，mm；Ta为齿轮副的中心距公差，mm；αn为齿轮压力角，(°)。

2.2 考虑齿轮侧隙的接触碰撞力模型

本文采用Lankarani和Nikravesh接触力模型(L-N接触力模型)，该模型的接触力公式为

(3)

式中Kδn为碰撞过程中的弹性变形力。其中K是接触刚度系数，δ是两接触物体间的相对压入量，n是碰撞力的指数，对于金属材料取1.5。K取决于接触面的材料和几何属性，当两个构件相接触时，K可由下式计算：

(4)

(5)

其中：μ和E分别表示碰撞件的泊松比和弹性模量；R1、R2为接触齿轮半径。

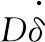
D=ηδn

(6)

其中η为滞后阻尼因子。在L-N接触力模型中，由于机构内部阻尼的存在，会导致接触碰撞过程中能量的耗散。根据能量守恒定律，在接触碰撞前后两物体的动能损失可表示为

(7)

对碰撞力进行积分同样可求得碰撞过程中物体的动能损失：

(8)

将式(7)和式(8)联立，可求得μ，进而可得

(9)

因此根据式(3)可得考虑齿侧间隙的齿轮副接触力FN为：

(10)

齿轮副的切向摩擦力采用ADAMS库伦摩擦模型：

(11)

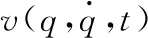
本文基于L-N接触力模型的碰撞力函数，在ADAMS中对齿轮侧隙的碰撞接触问题进行分析。

3 摆臂机构动态特性仿真及结果分析

3.1 仿真参数的设置与模型验证

摆臂变形机构ADAMS仿真模型如图3所示。轴2为输入构件，设置输入转速n2=120r/min。在Solidworks中建立装配体模型，将简化的装配模型导入到ADAMS中。导入后给各零件添加质量属性等，然后对其添加约束，如表1所示。

图3 摆臂变形机构ADAMS仿真模型

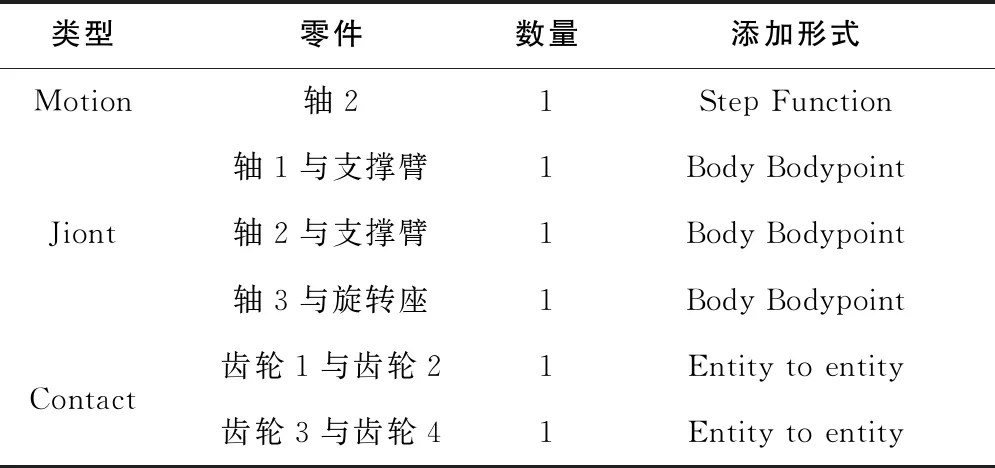
表1 主要零件间约束、驱动、接触统计

仿真计算得到轴3的角位移、角速度及齿轮1和齿轮2之间啮合法向力曲线，如图4-图6所示。

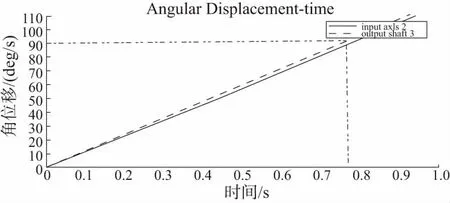
图4 轴2和轴3角位移时域图

图5 轴3角速度时域图

图6 齿轮1和齿轮2之间啮合法向力时域图

从图4可以看出，轮子由竖直位置旋转到水平位置时，大约需要0.75s，符合<1s的工作要求，同时可得输入轴与输出轴同步误差约为10′，≪1°的工作要求。图5表明，在运行之初，由于机构突然加速，两齿轮间会产生较大冲击，导致两齿轮间啮合力出现突变，大约0.1s后轴3角速度基本平稳下来，进入恒定转速阶段。图6显示，齿轮各轮齿间啮合力幅值在某一均值附近上下波动，这是齿轮以一定周期啮入、啮出冲击产生的结果。

时域分析中0.1s后轴3角速度和齿轮啮合法向力的理论计算值[7]和ADAMS仿真值，结果列于表2中。其中误差值是仿真和理论计算值的差值与理论计算值比值的绝对值。

表2 理论计算值和仿真分析值的比较

对比表2中各个参数，其理论值和仿真值的偏差较小，可认为二者基本吻合，从而验证了虚拟样机模型的正确性。

3.2 动力学仿真结果与分析

1)齿轮侧隙大小对机构动态特性的影响

为研究齿轮副侧隙[8-9]的大小对摆臂变形机构动态特性的影响，选取直齿轮副中侧隙1(图1)为研究对象。根据式(1)、式(2)计算得出直齿轮副的最小侧隙为0.083mm，最大侧隙为0.315mm。分别选取0mm(理想状态)、0.1mm、0.2mm、0.3mm 4种侧隙，设置仿真时间为1s，其余参数设置同3.1节[10]。

图7、图8、图9分别为齿侧间隙大小为0mm、0.1mm、0.2mm和0.3mm时齿轮接触碰撞力、摆杆角速度和角加速度随时间的变化情况(本刊系黑白印刷，如有疑问请咨询作者)。

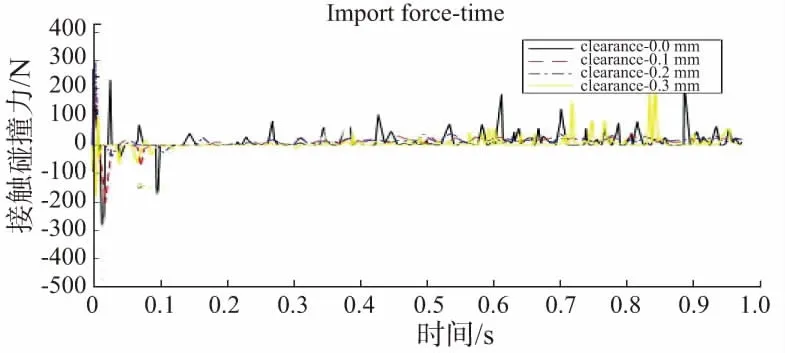
图7 齿轮1和齿轮2接触碰撞力时域图(不同侧隙大小)

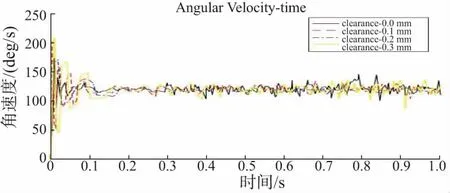
图8 摆杆角速度时域图(不同侧隙大小)

图9 摆杆角加速度时域图(不同侧隙大小)

图7显示，运动开始时，齿轮副接触碰撞力达到峰值，这是由齿轮速度突变引起的。当侧隙为0mm时，齿轮接触碰撞力最大。侧隙为0.1mm时，齿轮副接触碰撞力最小，约为133N，侧隙为0.3mm时，齿轮副接触碰撞力增大，接近200N，是侧隙为0.2mm时的1.2倍，是侧隙为0.1mm的1.5倍，碰撞力随侧隙的增大而增大。

图8表明，当齿轮侧隙为0.3mm时，角速度波动最为剧烈，当侧隙减小到0.1mm时，摆杆角速度波动明显趋于平缓，无侧隙时，角速度变化最为平稳。可见，随着侧隙的不断减小，摆杆角速度波动趋于平稳。

图9可以看出，摆杆角加速度波动较大。当侧隙为0.3mm时，摆杆角加速度峰值最大，接近80000deg/s2，曲线波动最为明显。侧隙为0.1mm时，峰值约为40 000deg/s2，是侧隙为0.3mm时的0.5倍。无侧隙时， 摆杆角加速度峰值最小。

造成以上现象的原因是：侧隙的产生使齿轮副产生“自由”和“接触”两种状态交替，导致侧隙碰撞力和摆杆角加速度增加，机构产生震动。侧隙为0mm时，齿轮一直“接触”在一起，不断进行着摩擦，加速系统能量的消耗，因此啮合力峰值比较大，加速度波动变化小；当侧隙为0.3mm时，齿轮之间不断交替“自由”和“接触”两种状态，机构震动比侧隙为0.1mm时更为剧烈，所以导致碰撞力峰值和角加速度变化明显。综上可得，控制齿轮侧隙在0.1mm左右有利于提高机构的工作性能。

2)齿轮侧隙数目对机构动态特性的影响

为研究侧隙数目对机构工作性能的影响，分别对单侧隙和双侧隙对机构进行动态特性仿真分析，设侧隙的大小均为0.1mm，其余参数设置同3.1节。

图10、图11、图12分别为单侧隙、双侧隙情况下齿轮接触碰撞力、摆杆角速度和角加速度随时间的变化情况。

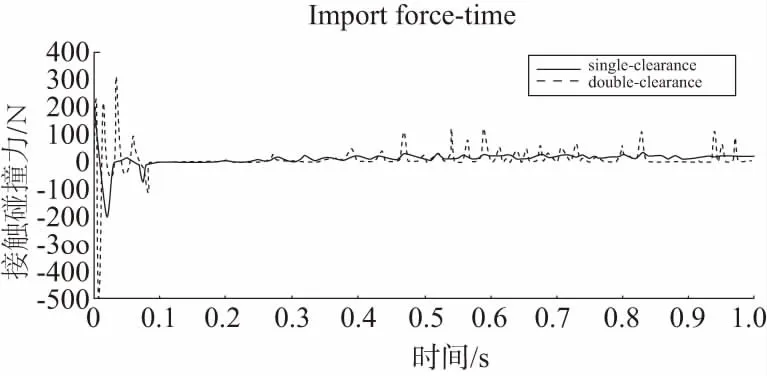
图10 齿轮1和齿轮2接触碰撞力时域图(不同侧隙数目)

图11 摆杆角速度时域图(不同侧隙数目)

图12 摆杆角加速度时域图(不同侧隙数目)

图10中，单侧隙情况下的碰撞力峰值是双侧隙情况的1.5倍。图11中，在摆臂机构变形0～0.1s的初始阶段，侧隙的数量对角速度影响不大，但整体变形过程中，单侧隙波动比双侧隙更加剧烈。图12中，单侧隙角加速度峰值约为40000deg/s2，约为双侧隙角加速度峰值的2倍。可以看出，相对于单侧隙，双侧隙的存在使得机构齿轮啮合副碰撞力、摆杆角加速度和角速度均表现为更小的数值，变形过程更平稳、更缓慢。

由于双侧隙的存在增加了系统能量的耗散，机构的势能经过齿轮副间能量的消耗后传递给摆杆，在一定程度上减弱了摆杆的动力学扰动。所以，大小合理的多齿侧间隙同时作用时，有利于提高摆臂变形机构的稳定性。

3)齿轮材料对机构动力学特性的影响

为研究不同齿轮材料对机构动态特性的影响，假定侧隙只存在直齿轮啮合副之间(侧隙1)，根据无人机的整体质量要求，选取齿轮1和齿轮2分别为聚甲醛(POM)、尼龙(MC901)和尼龙(PA66)3种目前市场上常用的塑料齿轮，分析3种材料齿轮机构的动力学特性，选择最合适齿轮材料。为了不改变摆臂变形机构的属性，仅改变齿轮的材料和接触参数，其他条件同3.1节不变。

经公式(4)计算，齿轮面对聚甲醛(POM)-聚甲醛(POM)的等效接触刚度K取值 2.3×108，尼龙(PA66)-尼龙(PA66)的K取值1.9×104，尼龙(MC901)-尼龙(MC901)的K取值1.5×104。

经公式(11)计算，齿轮面对聚甲醛(POM)-聚甲醛(POM)的动摩擦因数μd取2.1×104，尼龙(PA66)-尼龙(PA66)的动摩擦因数μd取1.6×104，尼龙(MC901)-尼龙(MC901)的动摩擦因数μd取1.2×104。

3种不同材料时齿轮副接触碰撞力、摆杆的角速度和角加速度随时间的变化情况见图13-图15。

图13 齿轮1和齿轮2接触碰撞力时域图(不同齿轮材料)

图14 摆杆角速度时域图(不同齿轮材料)

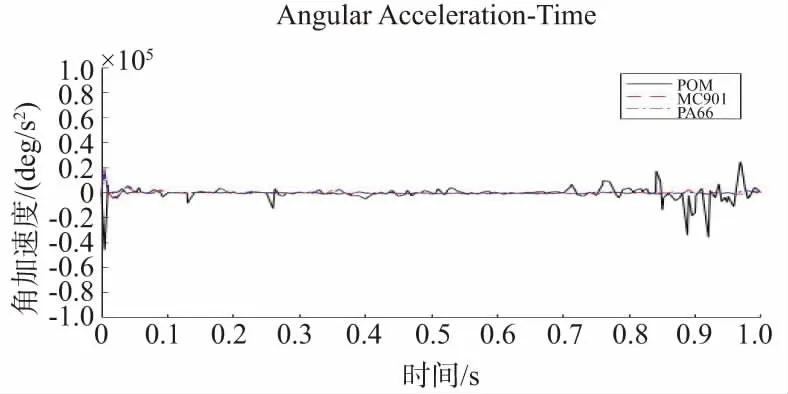
图15 摆杆角加速度时域图(不同齿轮材料)

图13显示，聚甲醛(POM)齿轮接触碰撞力幅值约为180N，约为尼龙(MC901)齿轮幅值4.5倍，约为尼龙(PA66)齿轮稳定阶段幅值3.5倍。因此尼龙(MC901)齿轮接触碰撞力峰值最小，啮合过程最为平稳，其次是尼龙(PA66)齿轮，聚甲醛(POM)齿轮接触碰撞力峰值最大。

图14显示，齿轮开始接触时，角速度波动比较明显，之后整体摆动过程比较平稳，只有微小波动。聚甲醛(POM)齿轮角速度幅值约为200m/s，约为尼龙(MC901)齿轮的1.7倍，约为尼龙(PA66)齿轮的1.3倍。聚甲醛(POM)齿轮角速度波动比尼龙(MC901)齿轮和尼龙(PA66)齿轮角速度波动要大。

由图15可以看出，当齿轮材料为聚甲醛(POM)时，摆杆角加速度峰值约是尼龙(MC901)齿轮峰值的2倍，约是尼龙(PA66)齿轮峰值的3.4倍。当齿轮为聚甲醛(POM)时，摆杆角加速度波动比较大，其次是尼龙(MC901)材料，尼龙(PA66)齿轮时摆杆角加速度波动最小，曲线相对光滑。

出现上述结果的原因是尼龙(MC901)齿轮啮合时，齿轮副的等效接触刚度和阻尼系数均减小，使得齿轮啮合接触力减小，由于接触碰撞消耗的能量也会减少，齿轮啮合碰撞力峰值更小。所以尼龙(MC901)-尼龙(MC901)接触时相对其他两种材料峰值更小，更合适作为齿轮材料。

4 结语

本文基于L-N接触力模型，并利用ADAMS软件，建立了摆臂变形机构的齿轮侧隙接触碰撞力模型，探究了齿轮侧隙大小、数量和不同齿轮材料对摆臂变形机构动态特性的影响。分析结果表明：

1)侧隙过大或过小，都会使碰撞力加剧，碰撞越剧烈，越会导致机构能量的耗散增加，从而减慢摆臂机构变形完成时间。当侧隙大小为0.1mm左右时摆杆展开冲击力较小，可在较快时间内完成摆杆变形工作，满足两栖无人机摆臂变形机构的性能要求。

2)侧隙越多，单一齿轮副碰撞力越小，摆杆角加速度波动越平稳。侧隙数量的增多，增加了机构耗散能量的速度，使机构展开的过程更加缓慢和平稳。机构中双侧隙的存在更有利于提升摆臂变形机构的动力学特性。

3)不同齿轮材料的质量和摩擦系数不同，摩擦系数降低会导致接触摩檫力的减小，减少能量消耗，提高机构运动平稳性。由上面分析可知，尼龙(MC901)为齿轮加工材料时，机构接触碰撞力较小，运动平稳，传动误差较小，更加符合机构的动态特性要求。