发射平台摆杆机构可靠性分析

，，，

(北京航天发射技术研究所，北京100076)

0 引言

随着新一代运载火箭的发展，发射流程应具备垂直组装、垂直测试、垂直转运(三垂模式)的能力。发射平台是实现三垂发射模式的重要一环，而摆杆机构又是发射平台的关键设备，主要用于铺设各种加注、供气、电缆、空调等管线路，在运输过程中摆杆保持各种管路、连接器、电缆的状态不变，起飞前带动脱落的连接器、管路、接头等摆开到安全范围之内[1-2]。因此摆杆机构功能的可靠性水平高低对保证发射平台是否具有三垂模式能力具有重要意义。由此可知对摆杆机构可靠性进行研究具有现实和迫切的工程意义，摆杆机构如图1。

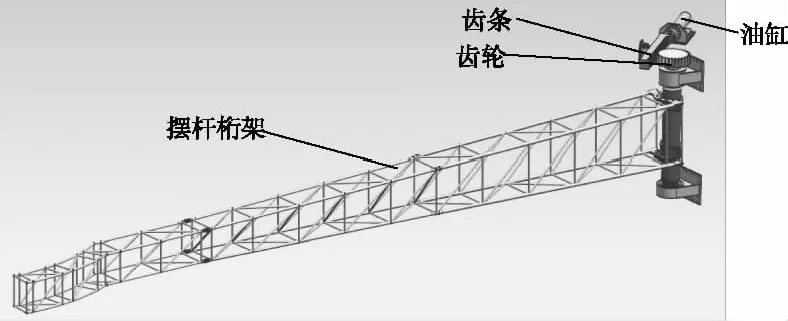
图1 发射平台摆杆机构

由于摆杆机构属于发射平台新研设备，尚未有文献对此类摆杆机构运动性能进行可靠性建模及计算，仅可以从文献[3-4]借鉴，分析类似机构运动可靠性的方法和思路。

本文从摆杆机构运动全过程出发，分析其运动机理，考虑摆杆机构实际受力情况，建立了摆杆机构启动失效、连续运动失效、运动不到位可靠性模型，并根据实际工程算例，计算出可靠性结果。

1 摆杆机构运动故障原因分析

图2 摆杆机构原理图

摆杆机构由液压油缸、齿条、齿轮、摆杆桁架等组成[5]，如图2。其工作原理是：液压油缸在液压油的作用下，向右伸出油杆，带动齿条向右运动，齿条与齿轮啮合，齿轮逆时针旋转，同时与齿轮固接的摆杆桁架从初始摆回状态运动到最终摆开状态，整个运动过程，角位移90°。通过分析其功能和组成特点，可看出摆杆机构是否工作正常与液压油压力、摆杆桁架铺设管路及连接器重力、摆杆桁架自重及风载等相互匹配有关。

在摆杆摆开的运动阶段，由于发射场的特殊环境以及摆杆桁架自身长、细的结构特点，气动载荷在摆开运动中变化较大，此外受桁架长、细特点，风载力矩在过程中同样也存在变化。这样可能存在液压油缸中的油杆无法克服阻力，而发生卡滞。同时，机构制造的误差、装配误差可能导致运动定位失效，使得摆杆无法摆开90°。摆杆摆开功能的正常实现，需要保证摆杆运动机构工作的各阶段，即启动、连续运动，运动到位三阶段的工作可靠，分析三阶段事件的故障表现及故障原因。

2 摆杆机构摆开过程可靠性建模

结合摆杆机构运动故障原因分析，建立了摆杆机构各阶段事件可靠性模型及求解方式。如表1所示。

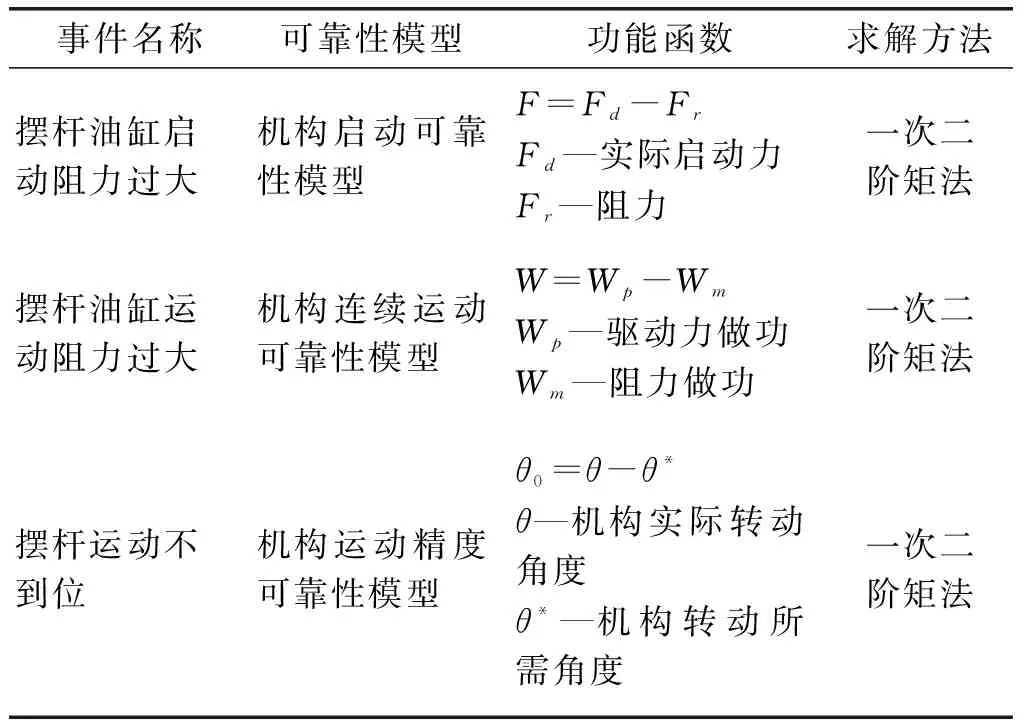
表1典型可靠性模型说明

2.1 摆杆油缸启动阻力过大

摆杆油缸为单向油缸，摆杆摆开运动方向如图3，正腔油压作用在活塞上，力为Fd，风载、摩擦力、反腔压力油压等阻力最终等效于作用在反腔活塞这一侧力Fr。在启动阶段，摆杆要实现摆开运动，必须保证Fd大于Fr，即摆杆在启动阶段可靠性系数为β1：

(1)

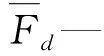
摆杆油缸启动阻力过大失效概率：

Pf1=1-Φ(β1)

(2)

式中：Φ(·)为标准正态分布函数。

图3 摆杆油缸示意图

2.2 摆杆连续运动阻力过大

在摆杆运动过程中，要使运动过程无卡滞、停顿，必须油杆速度大于0，保证齿条驱动齿轮转动，从而实现连续运动。在摆开过程中，驱动力Fd做功为Wp，阻力Fr做功Wm，Wp必须大于Wm，才能保证油杆速度大于0。如图4。

图4 摆杆油缸运动示意图

驱动功Wp与阻力功Wm分别为：

(3)

(4)

摆杆在连续运动阶段可靠性系数β2：

(5)

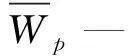
摆杆油缸连续运动阻力过大失效概率：

Pf2=1-Φ(β2)

(6)

式中：Φ(·)为标准正态分布函数。

2.3 摆杆运动不到位

摆杆运动机构，考虑其存在尺寸、磨损等偏差，使得其运动偏差具有一定的不确定性，其运动精度具有随机性，所以为保证摆杆桁架的运动精度，对其进行偏差分析和可靠性定量计算是非常必要的。摆杆机构齿条齿轮运动如图5所示，齿条运动到位实际行程为L，带动齿轮实际转动角度θ，几何关系式为：

θ=L/R

(7)

式中：R为齿轮半径。

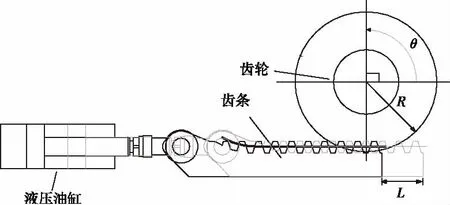
图5 摆杆机构齿条齿轮运动图

图6 摆杆桁架运动图

摆杆桁架转动角度即为齿轮实际转动角度θ，摆杆桁架运动图如图6所示：摆杆桁架长为l，摆杆摆回状态为OA，理论摆开状态为OA1，对应角度为θ*；OA2状态为摆开到位，对应角度为θ；OA3状态为摆开不到位，由几何关系可知，OA2状态下，对应的摆杆摆开位置间距ΔS大于0，考虑桁架为细长结构，有：

ΔS=(θ-θ*)·l

(8)

综合式(7)、(8)，有：

ΔS=(L/R-θ*)·l

(9)

摆杆运动不到位概率为：

Pf2=P{ΔS<0}

(10)

ΔS服从正态分布，有摆杆在运动到位阶段可靠性系数β3：

(11)

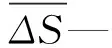
即摆杆运动不到位失效概率：

Pf3=1-Φ(β3)

(12)

式中：Φ(·)为标准正态分布函数。

3 工程算例

3.1 摆杆油缸启动阻力过大失效可靠性分析

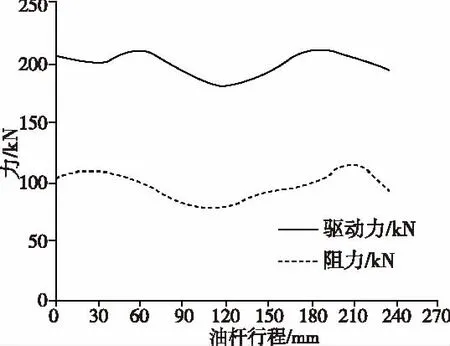
图7 驱动力、阻力与 油杆行程关系图

摆杆油缸力大小腔传感器实测数据，如图7。

将启动时刻(油杆行程为0 mm)数据代入(1)。取CFd=0.12，CFr=0.08，则摆杆在启动阶段可靠性系数为：

即摆杆油杆启动阻力过大失效概率为：

Pf1=1-Φ(β1)≈5.297×10-5

3.2 摆杆连续运动阻力过大失效可靠性分析

在摆杆运动过程中，当油杆运动到某一位移Lx时，活塞驱动功和阻力功分别为驱动力、阻力关于位移积分。

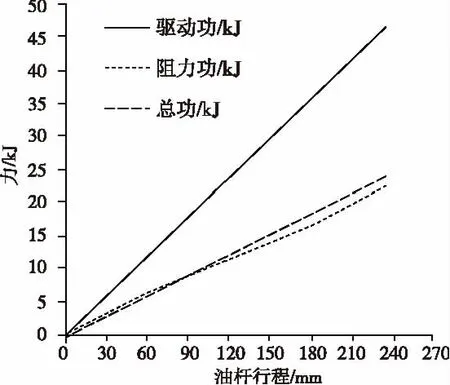
图8 驱动功、阻力功、总功与 油杆位移关系图

由图8可知，驱动功持续大于阻力功，将驱动功、阻力功数据代入式(5)(6)。取CWp=0.05，CWm=0.05，经计算可知摆杆油缸连续运动阻力过大失效概率为：Pf2≈0。

3.3 摆杆运动不到位

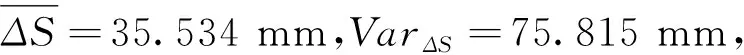
表2摆杆参数

摆杆机构运动失效概率：Pf=Pf1+Pf2+Pf3≈8.743×10-5，Pf<10-5，符合机构运动可靠性指标要求。

4 结论

1)结合摆杆机构运动功能分阶段特点，总结出机构运动失效可能出现的3类模式：摆杆油缸启动阻力失效、摆杆连续运动失效以及摆杆运动不到位失效，并分别建立相应可靠性模型，进行了可靠性计算；

2)对可靠性求解分析，摆杆在连续运动中发生卡滞失效可能性很小；存在摆杆油缸启动阻力过大失效和摆杆运动不到位失效的可能；

3)设计摆杆机构时，在不影响摆杆油缸腔体强度正常使用的前提下，可以通过提高油缸正腔压力来确保摆杆油缸启动功能正常；此外，须控制摆杆行程、齿轮半径及摆杆长度的加工精度，避免出现摆杆运动不到位失效。通过上述举措提高摆杆机构运动机构可靠性。