空间自由曲线的相似性比较方法

王道俊，王洪申

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

0 引言

在计算机视觉和模式识别中，形状相似性度量是一个重要的研究课题，在众多领域中具有广泛的应用，如图像检索、文字识别、目标识别、医学图像分析、人脸识别、机器人导航以及传感器网络等。在形状相似性度量问题中，两条曲线的相似性度量是基本问题。在进行模型的相似性评价时，研究人员通常对模型进行特征提取，即提取出能够代表模型本质特征的因素，再通过对模型特征的相似度计算评价模型的相似性。特征提取方法较多，其中形状分布算法[1]因其原理直观，性能鲁棒而被广泛采用。赵俊莉等[2]以平均测地距离作为评价依据，研究3D人脸形貌的相似性比较；马元魁等[3]以形体的形状分布曲线作为识别圆环体间形状差别的评价度量；ALCZAR J G等[4]运用曲线的曲率和挠率评价曲线间的相似性；BUCHIN K等[5]通过计算Fréchet 距离作为相似性度量，研究了运动曲线的相似性；吕科等[6]以解决空间曲线匹配来达到文物碎片的复原，运用轮廓线的哈希矢量分析曲线段的相似度。王坚等[7]针对封闭轮廓曲线，计算各采样点的弗朗内特标架和曲率值，利用曲率形成匹配点对，再通过对齐弗朗内特标架获得匹配矩阵，取匹配误差最小的矩阵作为最优匹配矩阵，实现空间曲线的匹配。孙晓鹏等[8]运用Minkowski距离作为相似测度，实现基于统计形状特征的三维耳廓点云识别。王洪申等[9]利用曲线的曲率分布描述空间曲线的几何特征，并以此衡量三维自由曲线的相似程度。

现有的形状分布算法通常是：1)定义一个函数，在三维模型上计算该函数值；2)统计函数值，将三维特征描述成函数值的二维分布图；3)根据二维分布图之间的距离作为相似程度依据。本文为了研究自由曲线间的相似性，计算曲线上的点到曲线形心的欧式距离作为描述函数，并将多个距离组成集合作为曲线的形状描述特征，然后直接计算集合之间的EMD(earth mover’s distance)距离，并以该距离作为评判相似性的依据。省去了常规形状分布算法的第2)步函数值的统计过程，从而减少了信息损失，更简洁、直观地实现了相似性的评价。

1 平面曲线和空间曲线的相似性评价算法

EMD即推土机距离，最初是为了解决运输问题[10]，该算法能通过一次线性规划计算出两个大小不同(或相同)的几何或向量的距离，可用于测量不同维特征向量之间的相似性。本文以沿曲线等弧长方向均匀取点，计算每个点到曲线质心的欧式距离，以该距离作为曲线的特征，使用EMD算法计算两个曲线特征之间的距离，以该距离的大小描述曲线的相似性。

设MC={Curve1,Curve2}是含有2个元素的一个自由曲线集合，通过运算比较集合中元素之间的相似性。算法步骤如下：

1)沿自由曲线Curvei(其中i=1时，表示自由曲线1，i=2时，表示自由曲线2)等弧长取相同的点数n，得到点集合表示为Pij={Pij，i=1，2；j=1，2，3，…，n；}，获得每个点坐标Pij(xi，j，yi，j，zi，j)。

2)计算自由曲线的质心Mi(i=1,2)，计算质心公式写成坐标分量形式，如下：

(1)

其中n为三维点的数量。得到Curve1的质心M1(x1，0，y1，0，z1，0)，Curve2的质心M2(x2，0，y2，0，z2，0)。

3)利用欧氏距离公式，计算自由曲线上等弧长所取每个点与质心Mi的距离，记为|pijMi|，得到自由曲线上等弧长取点距离的集合Di={di=|pijMi|,i=1,2;j=1,2,…,n}；

4)步骤3)中计算的每个距离集合代表了一条曲线特征，计算两个距离集合的EMD值，EMD值越小，曲线越相似。

记作：

δsim(Curve1,Curve2)=EMD(D1,D2)

(2)

2 算法验证实例

2.1 实验设计

为验证本文曲线相似性评价算法的性能，构造如表1所示的3组平面自由曲线模型和表2所示的3组空间自由曲线模型。其中：表1所示的3组平面曲线中，第1组为形状有微小差异的3条平面椭圆曲线，用人眼的直观相似性评价，曲线2和曲线3更相似，计算值应满足式(3)；第2组为形状有微小差异的平面B样条开曲线，用人眼的直观相似性评价，曲线1和曲线2更相似；第3组为形状有微小差异的平面B样条闭曲线，用人眼的直观相似性评价，曲线1和曲线2更相似。第4、第5组为形状有微小差异的空间B样条开曲线，第6组为形状有微小差异的空间B样条闭曲线。第2组至第6组实验，以人眼直观观察，实验结果应满足式(4)。实验中，分别在每条曲线上以等弧长方法取相同数量的点(设取点数量为m)，计算所取点与曲线质心的欧氏距离，作为EMD度量的参数，将平面曲线和空间曲线上得到的欧氏距离的依次带入式(2)，计算两两曲线的EMD值。

δsim(Ellip2,Ellip3)<δsim(Ellip1,Ellip2)<δsim(Ellip1,Ellip3) (3)

δsim(Curve1,Curve2)<δsim(Curve2,Curve3)<δsim(Curve1,Curve3)

(4)

表1 算法对平面曲线有效性验证实验

表2 算法对空间曲线有效性验证实验

2.2 实验结果与讨论

1)针对平面曲线的算法有效性验证

应用构造的第1-第3组平面曲线，设计3组实验，验证算法的有效性与可行性。由式(2)计算两平面曲线的EMD值，根据所取点数的不同，得到表3所示的实验数据。所得实验数据满足式(3)、式(4)，与人的直观评价一致。

表3 算法对平面曲线有效性实验数据

2)针对空间曲线算法有效性验证

运用构造的第4-第6组空间曲线，设计3组实验，验证算法的有效性与可行性。由式(2)计算两曲线的相似度量值，根据所取点数的不同，得到表4所示的实验数据。所得实验数据满足式(3)、式(4)，与人的直观评价一致。

表4 算法对空间曲线有效性实验数据

3)算法鲁棒性验证

应用构造的第3组平面曲线的Curve1、Curve2和第5组空间曲线的Curve1、Curve2，分别设计3个实验，验证算法对平移和旋转的鲁棒性。组号分别记为X-Ⅰ、X-Ⅱ、X-Ⅲ(X取3、5)。X-Ⅰ组不进行任何变换，比较两曲线的相似性；X-Ⅱ组曲线Curve1与Curve2分别平移不同的距离，比较两曲线的相似性；X-Ⅲ组曲线Curve1与Curve2分别进行旋转变换，比较曲线的相似性。实验结果如表5所示，X-I组和X-II组的相似值相同，表明相似性评价结果与曲线的平移无关；X-I组和X-III组的实验数据对比可知，相似性评价结果与曲线的旋转无关。因此，算法具有平移、旋转不变性。

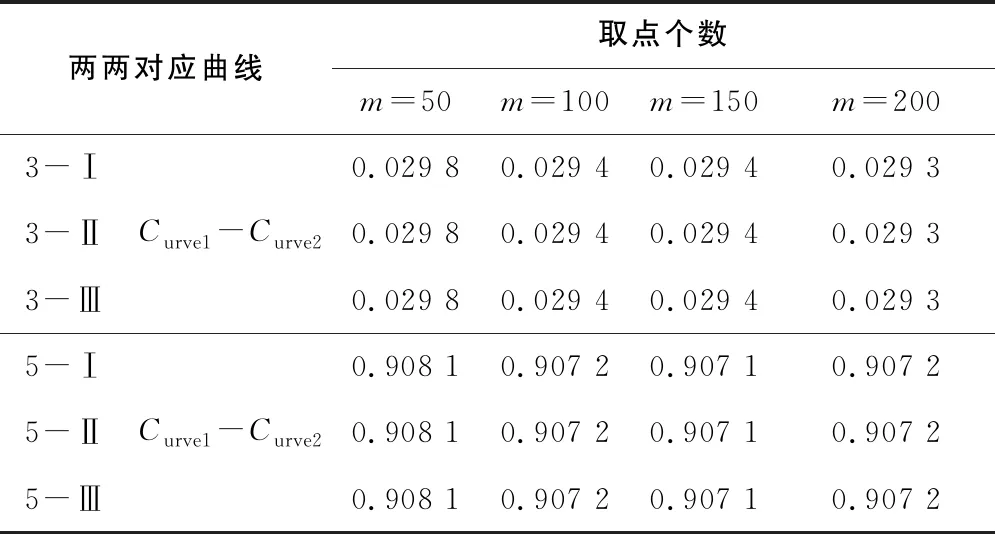
表5 算法鲁棒性实验数据

3 结语

本文提出了曲线的相似性评价算法，适用于平面曲线和空间曲线。首先在曲线上取点计算该点到曲线质心的欧氏距离，作为该曲线的特征，然后用EMD算法计算曲线特征的距离，用于度量空间曲线的相似性，计算简便，方法可靠。算法评价的空间曲线相似性结果符合人的感官判断，能够很好地反映空间曲线的相似程度。通过大量的实验验证，算法可行有效。