限位条件下直轨倒立摆摆起控制量的分析研究

侯祥林,朱宸邑,张凤众,张啸尘

(1.沈阳建筑大学机械工程学院,辽宁 沈阳 110168;2.沈阳建筑大学电气与控制工程学院,辽宁 沈阳 110168)

倒立摆装置是指物体处于倒立不稳定状态并且可以通过人为控制达到动态平衡状态的装置。它是抽象的控制问题,在结构上表示为重心在上,支点在下的装置。倒立摆按照类型分为旋转式、直轨式、圆轨式、滚轮式和平面式[1-7]。

倒立摆系统的控制研究包括摆杆的摆起控制和摆杆的平衡控制。对倒立摆系统的最初研究始于对摆杆的平衡控制问题。但倒立摆系统的摆起控制也一直是学者研究的热点课题。T.Takahashi[8]率先开始研究倒立摆系统的摆起控制问题;黄南辰[9]针对旋转倒立摆提出了一种规则分析摆起控制方法;侯祥林等[10]对圆轨一级和直轨二级倒立摆系统的摆起控制进行了研究和仿真分析;罗晶等[11]对一级倒立摆系统的PID控制进行了分析研究;韩东方等[12]对直轨一级倒立摆系统的控制及实现进行了研究。常见的摆起控制方法有:手动控制、智能仿人控制策略、基于规则分析的控制策略、基于能量方法等[13-18]。

直轨倒立摆系统由作平动的小车和作平面运动的一个摆杆构成,2个自由度系统[19-21]。近年来,国内外对直轨倒立摆系统的摆起控制基于试验建模的模糊控制和能量控制较多,基于机理建模的研究较少,倒立摆系统运动力学模型也未对导轨存在限位情况进行单独分析和研究。另一方面,倒立摆系统的摆起控制过程中,系统持续进行加载,出现加载冗余现象,倒立摆系统的摆起过程需要进行多次的往复运动最终才能实现摆起控制。基于此,笔者对限位条件下的倒立摆系统进行模型受力和行为分析,根据分析力学和达朗贝尔定理,建立直轨一级倒立摆系统在导轨有限位情况下系统动力学微分方程,以摆起终点为目标,从实验观测出发,研究在导轨存在限位的基础上倒立摆系统通过短时加载方式来实现倒立摆系统的摆起控制问题,从而有效降低倒立摆系统控制量出现冗余情况,提高倒立摆系统的摆起控制效率。

1 导轨有限位倒立摆力学模型

1.1 系统模型及参数

直轨倒立摆系统的导轨分为有限位和无线限位两种情况,其简化模型如图1所示。设小车质量为m,受的阻力为F0,它包括由库仑阻力和黏性阻力,设摩擦系数为μ,黏性阻力系数为c,驱动力为F(t);摆杆的质量为m1,对其质心C1转动惯量为JC1,质心C1到O1轴的距离为lC1,小车的位移为x,摆杆转角为θ1。

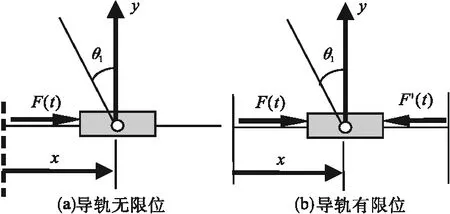
图1 直线一级倒立摆简化模型Fig.1 The simplified model of single linear inverted pendulum

1.2 运动分析

由小车的坐标表示出摆杆的质心坐标:

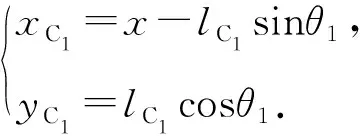
(1)

摆杆质心C1的速度和加速度:

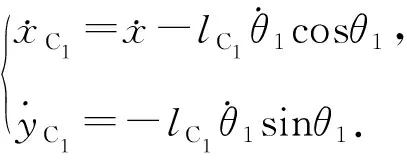
(2)

(3)

1.3 受力分析

摆杆、小车的受力分析如图2、图3所示,每个摆杆受重力作用。

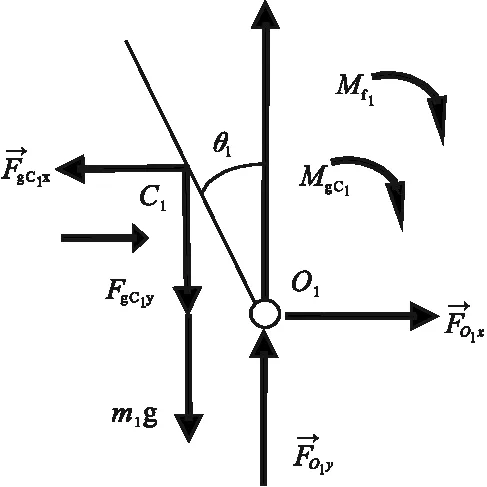
图2 直轨一级倒立摆摆杆受力分析Fig.2 The mechanical model of lower pendulum for single linear inverted pendulum

图3 直轨一级倒立摆小车受力分析图Fig.3 The mechanical model of translating slide for single linear inverted pendulum

1.4 惯性力分析

摆杆惯性力:

(4)

小车惯性力:

(5)

1.5 应用达朗贝尔原理,列平衡方程

(1)摆 杆

(6)

式中:c1为转动阻尼系数。

(2)小 车

小车竖直方向所受合力方程∑Y=0,小车水平方向所受合力方程∑X=0,整理可得:

(7)

当考虑小车受到阻力与库仑摩擦阻力,且随着小车的速度方向进行变化,与小车的运动速度方向相反,即:

(8)

倒立摆系统加载小车受力分析如图4、图5所示。

图4 倒立摆系统向右加载小车受力分析Fig.4 The force analysis of the inverted pendulum system with loading to the right of the trolley

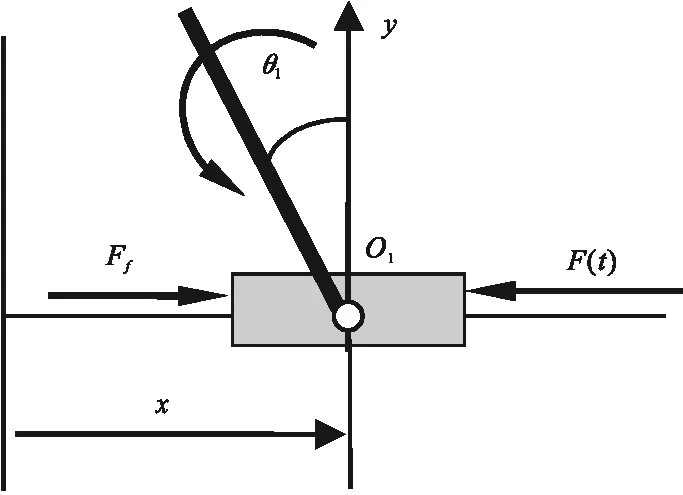
图5 倒立摆系统向左加载小车受力分析Fig.5 The force analysis of the inverted pendulum system with loading to the left of the trolley

通过式(6)、式(7)、式(8)可得如下微分方程:

(9)

2 倒立摆系统摆起策略

2.1 倒立摆系统行为分析

直轨倒立摆系统在导轨限位条件下,摆起阶段在控制时,存在控制量过大,小车和摆杆将会出界情况;控制量过小,小车和摆杆一直缓慢加载,控制量存在冗余情况,此时系统控制量又需要反复进行修正,增加了摆起时长。

在满足倒立摆系统摆起能量的前提下,短时加载后利用倒立摆系统中的惯性继续运动,待倒立摆系统的摆杆处于垂直向下时再进行加载,反复短时加载,从而实现倒立摆摆起状态,即倒立摆系统的摆杆处于垂直向上相对静止的状态。这样既可以保证小车不出界(即小车加载后位移在导轨长度的一半区域内活动),又可以缩短摆起时长达到摆起目的。

小车行为:小车在受到倒立摆系统短时加载时,小车产生加速度。在力的作用下,小车沿着加载力的方向进行加速。受到系统的摩擦阻力等原因小车速度将逐渐减小。

摆杆行为:小车在受到倒立摆系统短时加载时,小车产生加速度,摆杆此时会产生反向惯性力。系统向右加载时,摆杆顺时针摆动。系统向左加载时,摆杆逆时针摆动。

2.2 倒立摆系统模型简化分析

根据式(9),忽略摩擦系数μ和转动阻力系数c1,可得:

(10)

加载冲量的总和等于小车动量的变化量:

FΔt=mv-mv0.

(11)

小车向前运动,速度越来越快,随后不加载,小车无加速度,受到阻力影响,小车将越走越慢,速度减小。

2.3 基于状态观测摆起控制的策略分析

摆起状态目标:通过合理加载,小车在导轨范围内运动,摆杆达到竖直向上,摆杆速度趋近0 m/s,摆杆角速度趋近0 rad/s的状态。即:

(12)

倒立摆系统的摆杆初始状态为竖直向下状态,对倒立摆系统向右短时加载,小车向右平移,摆杆顺时针进行摆动。无加载时摆杆受到重力和阻力,摆杆会达到左侧最高点随后逆时针进行摆动。在摆杆摆动到左侧最低点时,对倒立摆系统向左短时加载,小车向左平移,摆杆逆时针进行摆动,并达到最高点。如此对倒立摆系统反复加载,摆杆将摆动至竖直向上的状态。

(1)当摆杆处于竖直向下状态时,对小车向右短时加载,此时摆杆顺时针摆动,摆杆的速度和摆杆的角速度顺时针逐渐增加(见图6)。

图6 倒立摆系统向右短时加载运动分析Fig.6 The motion analysis with loading to the right of the inverted pendulum system for a short time

(2)当无加载时摆杆受到重力和阻力,摆杆的速度和摆杆的角速度顺时针慢慢逐渐减小并达到左方的最高点,此时摆杆角速度为0。接着摆杆逆时针反向摆动,摆杆的速度和摆杆的角速度逆时针逐渐增加(见图7)。

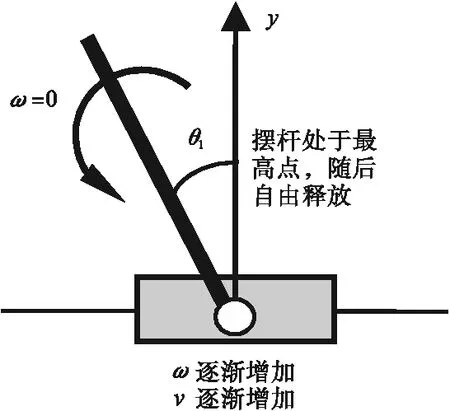
图7 倒立摆系统向右短时加载后无加载时运动分析Fig.7 The motion analysis without loading after loading to the right for a short time

(3)当摆杆处于竖直向下状态时,对小车向左短时加载。加载时考虑以此加载后小车是否会超过导轨行程的一半。此时摆杆继续向右进行摆起,摆杆的速度和摆杆的角速度逆时针继续增加(见图8)。

图8 倒立摆系统向左短时加载运动分析Fig.8 The motion analysis with loading to the left of the inverted pendulum system for a short time

(4)当无加载时摆杆受到重力和阻力,摆杆的速度和摆杆的角速度逆时针逐渐减小并达到左方的最高点,此时摆杆角速度为0。接着摆杆顺时针反向摆动,摆杆的速度和摆杆的角速度顺时针逐渐增加(见图9)。

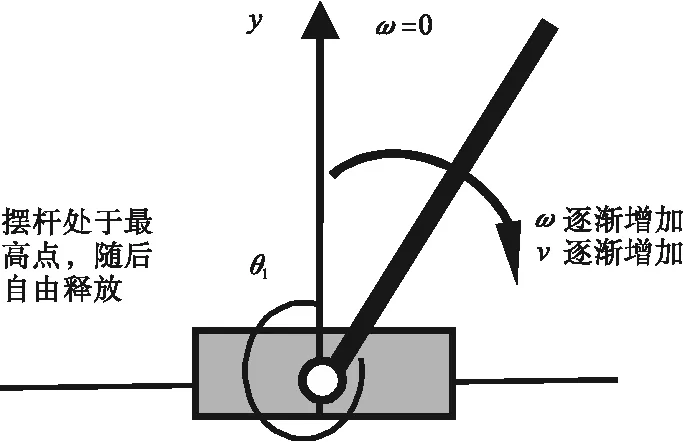
图9 倒立摆系统向左短时加载后无加载时运动分析Fig.9 The motion analysis without loading after loading to the left for a short time

如此反复短时加载,摆杆将会越摆越高,逐渐达到最高点,摆杆角度为0度或360度,摆杆速度为0 m/s,摆杆角速度为0 rad/s,小车始终在行程范围内。

3 倒立摆系统摆起模型仿真分析

3.1 系统参数及初始条件

系统参数:设定摆杆质量为m1=0.109 kg;小车质量为m=1.096 kg;摆杆转动轴心到杆质心的距离为lC1=0.25 m;摆杆的转动惯量为JC1=0.002 23 kg·m2;摩擦因数为μ=0.21;转动阻尼系数为c1=0.05 N/(m·s-1);黏性阻力系数为c=0.000 21 N/(m·s-1)。

3.2 摆起控制仿真

在进行直线一级倒立摆摆起控制仿真实验时,需要首先对程序进行初始化设置,这里将摆起控制计算的时间步长设定为0.02 s。依据倒立摆系统能量守恒和电机输出扭矩,小车的不超过导轨限长等前提下,对倒立摆系统进行计算,当载荷为15 N时,可通过反复左右加载使倒立摆实现摆起状态。倒立摆系统的摆起加载控制力随时间变化如表1所示。由表可知摆起过程中每隔0.02 s加载控制力的情况。

表1 摆起过程加载力列表Table 1 The loading power during the swing-up process

图10为小车位移随时间变化曲线。由图可知,整个摆起过程小车左右运动的总行程在0.5 m左右,在导轨限位0.64 m范围内。图11为摆杆转角随时间变化曲线。由图可知,倒立摆系统经过短时加载,摆杆从竖直向下的位置摆动至竖直向上的位置,趋近于360度的角度,即摆起位置。图12为小车速度随时间变化曲线,摆起过程中小车速度一直在进行变化,最后趋近于0状态。图13为摆杆角速度随时间变化曲线,摆起过程摆杆角速度一直在进行变化,最终趋近于0状态。

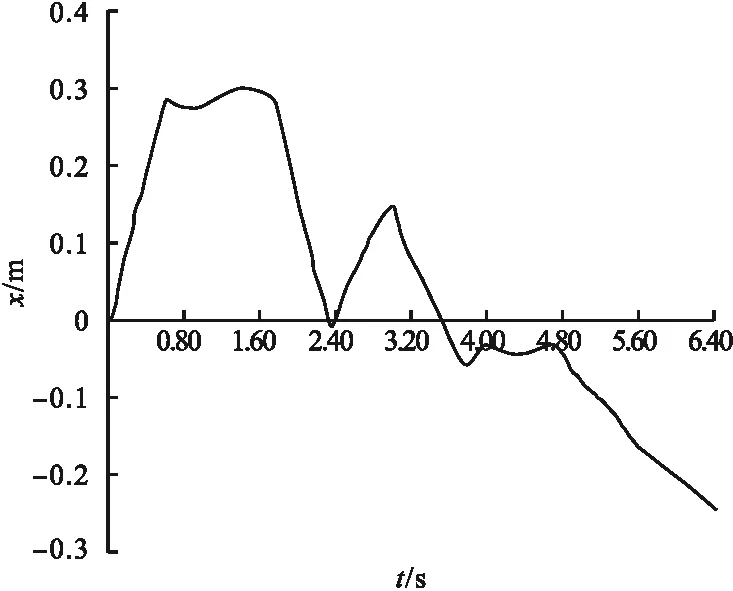
图10 摆起过程小车位移随时间变化曲线Fig.10 The displacement-time curve during swing-up process

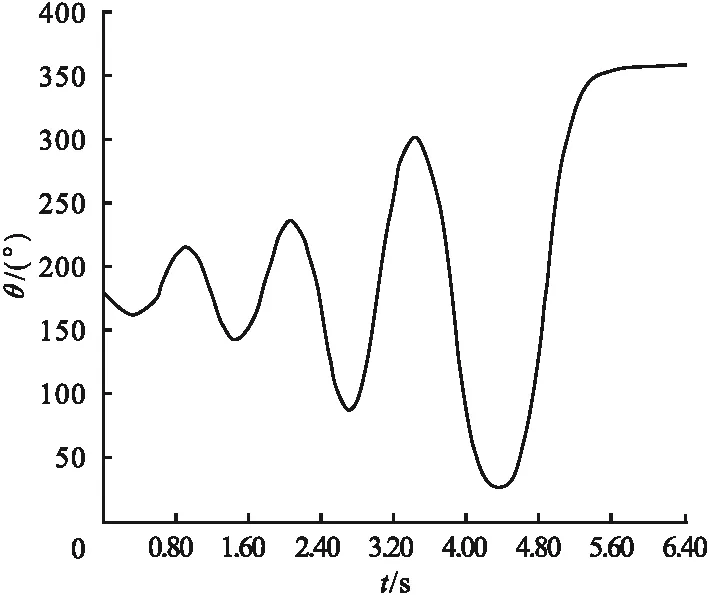
图11 摆杆转角随时间变化曲线Fig.11 The angle-time curve during swing-up process

图12 小车速度随时间变化曲线Fig.12 The velocity-time curve during swing-up process

图13 摆杆角速度随时间变化曲线Fig.13 The angle velocity-time curve during swing-up process

经过计算和仿真后,可以看出对系统进行了14次加载,7次正向向右加载,7次反向向左加载。因即将到达倒立摆系统摆起平衡位置时,荷载15 N始终无法满足倒立摆系统摆起条件,因此在倒数两次加载变成了-11 N和5 N,这样加载优化可以在满足倒立摆系统条件的前提下经过7次向左向右地摆起,在6.14 s内实现摆杆的摆起过程,达到倒立摆系统的摆起状态,并保持相对稳定状态。

4 结 论

(1)直轨倒立摆在导轨限位条件下,基于状态观测对其进行短时加载,成功实现了倒立摆的摆起控制。倒立摆系统短时加载控制是可行的,可为多级倒立摆系统的摆起控制提供参考。

(2)通过短时加载的数据分析可知,倒立摆系统的摆起控制在导轨有限长且载荷会存在加载冗余情况。因此,在即将摆起时减小加载控制量,能有效降低倒立摆系统控制量出现冗余情况,提高倒立摆系统的摆起控制效率。