外骨骼上肢康复机器人滑模控制策略研究
2021-08-13管瑞欣
管瑞欣
(陕西铁路工程职业技术学院,陕西 渭南714000)
0 引言
目前,社会人口老龄化严重,且由于一些自然和非自然事件的发生,例如:交通事故、地震和工作中操作机械失误等均会造成人类肢体不同程度的运动障碍[1-2]。因此,目前社会需要大量的康复医疗设备。
康复设备不但减轻了康复医疗师的工作压力,而且工作效率高。康复医疗师采用人工康复训练均是通过经验来施加作用力的,但是康复设备不但可以解放康复医疗师,而且可以高精度地完成康复训练的任务。
目前,研究较多的康复设备主要包含两个类型:一是绳索驱动康复设备;另一个是外骨骼型的康复设备。由于绳索驱动康复设备工作空间有限,运动精度高,而且重构能力很好,因此,绳索驱动康复设备也吸引了很多学者的兴趣:合肥工业大学訾斌团队设计了绳索驱动并联机器人,主要应用于3D打印和腰部的康复训练;还针对系统刚度分布和控制策略等进行了研究,并通过实验测试进行了验证[2-3]。哈尔滨工程大学张立勋教授、王克义教授和王砚麟博士等对绳索驱动康复机器人的控制策略和系统的运动稳定性等问题进行了研究,分别针对平面构型和空间构型进行了研究[4-8]。
但是,绳索驱动康复机器人中绳索只能提供单方向的张力,绳索的柔性会降低系统的刚度,对绳索驱动康复机器人的控制并实现患者安全性具有很大的挑战。而骨骼型的康复及机器人不存在这个问题,因其具有人机交互契合度高、运动舒适性和灵活性好的性能特点,使得外骨骼型的机器人在工业、康复和军事领域均具有很好的应用前景[9-11]。
广西科技大学高学山团队研究了一款两自由度下肢康复机器人,结合模糊PID和传统PID控制方法进行研究[12],并进行了实验分析。汪浩然使用不完全微分PID算法设计了一种双闭环控制器,内环采用PI算法进行速度控制,外环采用PD算法进行机器人的位置控制[13]。
南京航空航天大学吴青聪团队研究了一款软质康复外骨骼机器人,在关节处引入了柔性驱动环节,并设计了模糊神经网络阻抗控制算法,通过定阻抗和变阻抗的实验研究[14],变频率复制训练时关节转矩提升88.3%和57.6%,可以很好地改善康复机器人的稳定性。
本文介绍了一种外骨骼上肢康复机器人,在运动学和动力学的基础上,设计了一种基于名义模型的滑模控制器,并通过实例仿真进行了控制效果的验证。结果表明控制效果可以满足上肢康复训练的基本要求。
1 外骨骼上肢康复机器人运动学
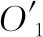

图1 上肢结构、运动关系和外骨骼机器人构型
如图1所示,在肩关节处建立坐标系O-xy,其中:q1和q2分别表示肩关节和肘关节的角位移;O1表示外骨骼上肢康复机器人末端在工作空间中的位置(即腕关节的位置);m1和m2分别表示外骨骼上肢康复机器人大臂和小臂的质量。上肢大臂和小臂的运动由外骨骼上肢康复机器人的肩关节和肘关节处的电机驱动,实现康复机器人的大、小臂的运动。
由图1可知,外骨骼上肢康复机器人末端在工作空间中的位置O1可以表示为
(1)
则以下关系式可以得到
(2)
从而可以得到
(3)
由图1可以得到
(4)
根据余弦定理,由图1可知
(5)
进一步得到
(6)
假设x=[x1,y1],q=[q1,q2],则存在以下关系式:
(7)
式中J为外骨骼上肢康复机器人雅克比矩阵,可以表示为
(8)
通过计算可得:
因此,外骨骼上肢康复机器人雅克比矩阵和机器人结构有关。
2 动力学分析
为实现外骨骼上肢康复机器人的运动控制,需要进一步将关节角的动力学方程转化为关于机器人末端位置的动力学方程。
根据虚功原理[10]可知,在静态平衡状态下,外骨骼上肢康复机器人末端的作用力Fx和关节力矩τ之间存在如下关系:
Fx=J-Tτ
(9)
由方程式(7),可得
(10)
因此,
(11)
一般关节型刚性机器人的动力学模型可以写为
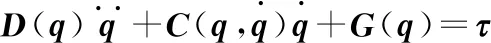
(12)

将式(9)-式(11)代入方程式(12),并进一步整理可得外骨骼上肢康复机器人的动力学模型:
(13)
其中
3 滑模控制器设计

(14)

设计的滑模面函数为
(15)
则滑模控制器设计为
(16)
式中K>0,为增益矩阵。
将控制律式(16)代入外骨骼上肢康复机器人的动力学模型式(13),可以得到
Gx(q)+Ks
(17)

(18)
此外,由于Dx(q)是对称且正定的,因此,定义Lyapunov函数为
(19)
则有
(20)
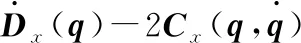
(21)
将式(21)代入式(20)并进行整理,得到
(22)
则
(23)
式中:λmin和λxmax分别表示K的最小特征值和Dx(q)的最大特征值,且λ>0,则方程式(23)的解为
V(t)≤e-2λ(t-t0)V(t0)=e-2λ(t-t0)V(t0)
(24)

4 实例仿真分析
分析控制策略的可行性,在MATLAB/Simulink中搭建上肢康复机器人的控制仿真实验模型,并通过以下具体实例进行分析。上肢康复机器人具体结构参数如下:l1=l2=0.5m,外骨骼上肢康复机器人的大、小臂质量分别为m1=1.24kg和m2=0.92kg,末端的负重为0.5kg;重力加速度g=9.8m/s2。
假设上肢康复机器人末端的运动期望轨迹为
(25)

外骨骼上肢康复机器人的控制结构如图2(a)所示,其中控制器采用式(16)所示的滑模控制律,通过检测外骨骼下肢康复的运动状态并进行反馈,和运动期望进行比较,得到实际跟踪轨迹的运动误差作为滑模控制器的输入,最后由控制器控制外骨骼上肢康复机器人的运动,进而实现闭环控制。
在MATLAB/Simulink中搭建上肢康复机器人的控制仿真实验模型如图2(b)所示,其中Sliding_model_ctrl模块和Robot_model模块分别表示通过S-Function编写的滑模控制算法模型和上肢康复机器人模型,Desired_trajectory表示给定的运动期望,如式(25)所示。
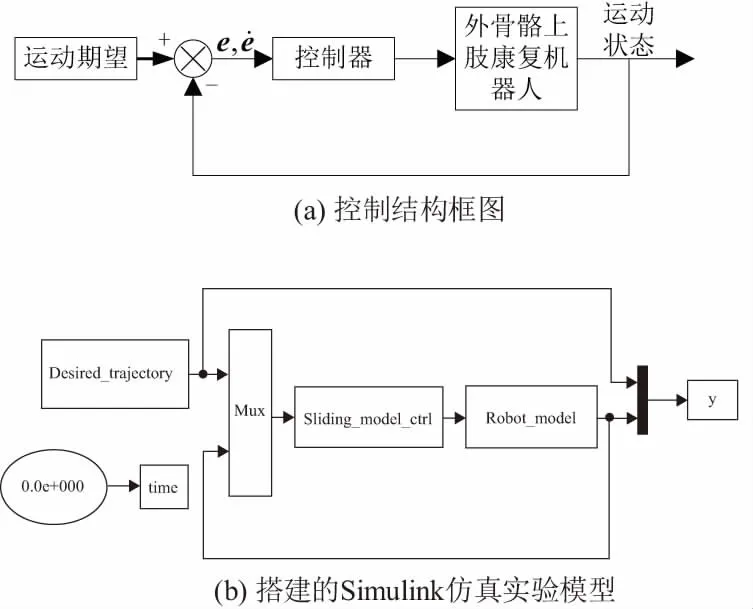
图2 控制结构框图和仿真实验模型
通过设置仿真模型的结构参数和控制器参数,对上肢康复机器人滑模控制器的轨迹跟踪性能进行实验验证。在上述滑模控制器的作用下,外骨骼上肢康复机器人的运动状态如图3-图6所示。图3为外骨骼上肢康复机器人的末端位置变化曲线,由于机器人末端的初始位置为(1,1)m,而期望轨迹的初始位置为(1,1)m,位置误差导致在机器人初始的运动误差较大,特别是y1的误差更为明显,但是大约在0.38s处机器人可以很好地跟踪期望的运动。

图3 末端位置跟踪曲线
图4为外骨骼上肢康复机器人末端运动速度变化曲线。同样,由于实际初始位置和期望运动的初始位置的差别,导致机器人末端的运动速度在开始运动时误差较大,但大约在0.38s以后,机器人末端的运动速度可以很好地跟踪期望的运动。
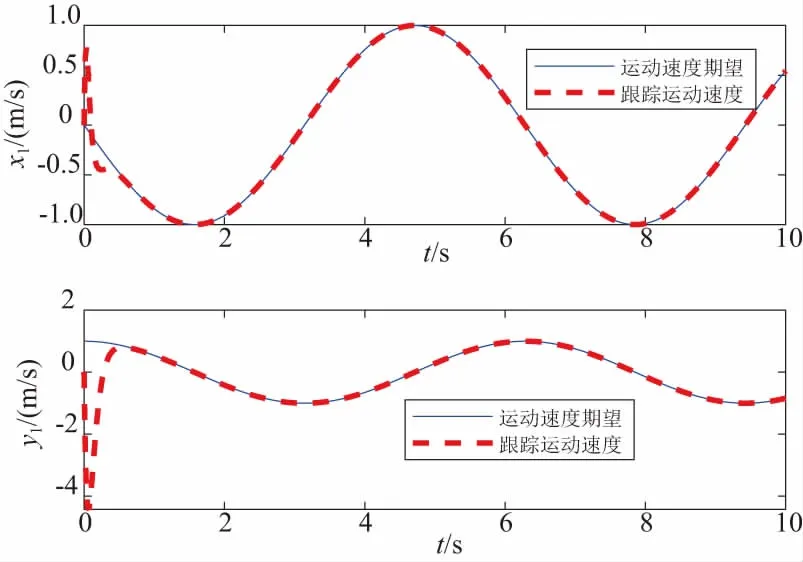
图4 末端速度跟踪曲线
图5为康复机器人大、小臂末端作用力Fx和关节驱动力矩τ的变化曲线,肩关节的驱动力矩在开始运动时存在较大的抖动,而且康复机器人小臂末端输出的作用力也在开始运动时存在较大的抖动,这也是由于实际初始位置和期望运动的初始位置的差别所导致的。大约在0.38s以后关节力矩和大、小臂末端的输出力变化是平缓的。
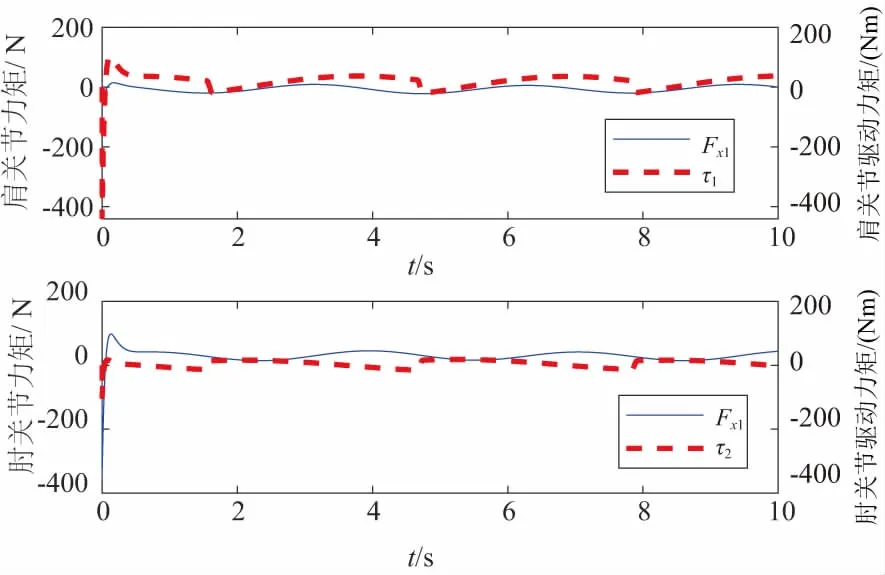
图5 Fx和τ变化曲线
图6为上肢康复机器人末端的运动轨迹跟踪曲线,图7为康复机器人末端的运动误差。由图可知,在初始运动时,由于y方向的初始位置和期望位置相差较大,因此运动误差较大,但在0.32s以后,康复机器人末端的实际运动可以很好地跟踪期望的运动。综上所述,设计的滑模控制器对康复机器人的运动具有好的运动控制效果,可以满足上肢康复训练的基本需求。

图6 运动轨迹跟踪效果

图7 运动误差
5 结语
针对外骨骼上肢康复训练的需求,介绍了一款两自由度外骨骼上肢康复机器人。为了实现对外骨骼上肢康复机器人的实时控制,在机器人的运动学和动力学的基础上,设计了滑模控制器对康复机器人进行控制。通过仿真实验验证了所设计的控制器对康复机器人的运动具有较好的控制效果,可以满足上肢康复训练的要求。
