离散alpha偏正态分布：性质和参数估计

魏正元，彭天奎，周晓娅，刘 美

（重庆理工大学 理学院，重庆 400054）

2010年，Elal-Olivero［1］首次提出了alpha偏正态分布（ASN），记为X～ASN（α），它比正态分布和偏正态分布（SN）［2］更灵活，其概率密度函数和生存函数如下：

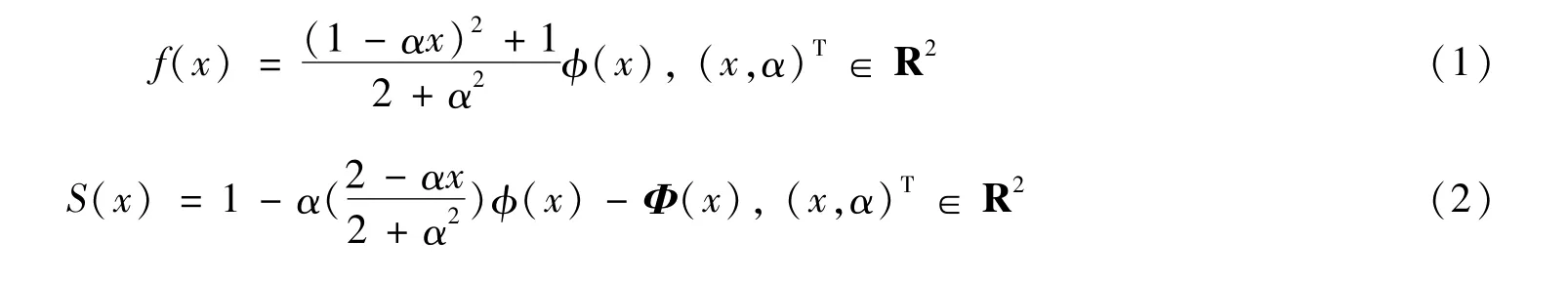
式中：参数α控制该分布的偏度和峰度，等式（1）的图像随着参数α的改变可以呈单峰和双峰的形状，因此用ASN分布来拟合双峰有偏的数据是可行的。然而，由于所观测到的样本几乎都是离散的，用连续分布来拟合样本可能会出现一些偏差，那么，使用ASN分布的离散对应物来拟合离散数据是具有研究价值的。

设连续随机变量X的生存函数为SX（x）=P（X≥x），令Y=（下取整函数），那么随机变量Y具有概率质量函数：

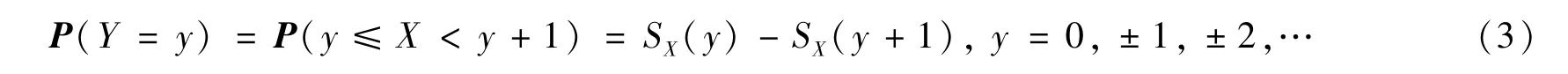
连续分布离散化相关问题研究一直受到国内外诸多学者的关注。Nakagawa等［3-4］研究了离散Weibull分布；Jazi等［6-7］研究了离散可逆Weibull分布和离散可逆Rayleigh分布；Chakraborty等［8］定义了离散gamma分布，Chakraborty等［9-10］在此基础上提出了离散广义gamma分布，同时研究了离散幂分布。Barbiero［11］讨论了连续二元概率分布的离散化方法并给出了二元指数分布的应用实例。此外，王家华等［12］讨论了连续分布离散化在风险分析中的应用，任美芳等［13］研究了离散化泊松—指数混合分布并讨论了它的性质和参数估计，本文中通过等式（3）提出了离散alpha偏正态分布，它包含了Roy［5］提出的离散正态分布。

1 离散alpha偏正态分布

定义1若离散随机变量Y具有如下概率质量函数

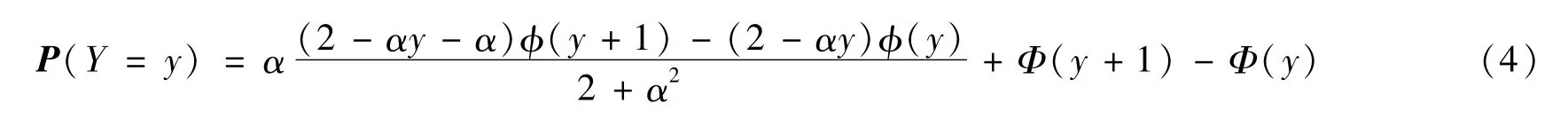
式中：y=0，±1，±2，…，α∈R，称Y服从离散alpha偏正态分布（DASN），记Y～DASN（α）。

注1由定义Y=，X～ASN（α）及等式（3），有

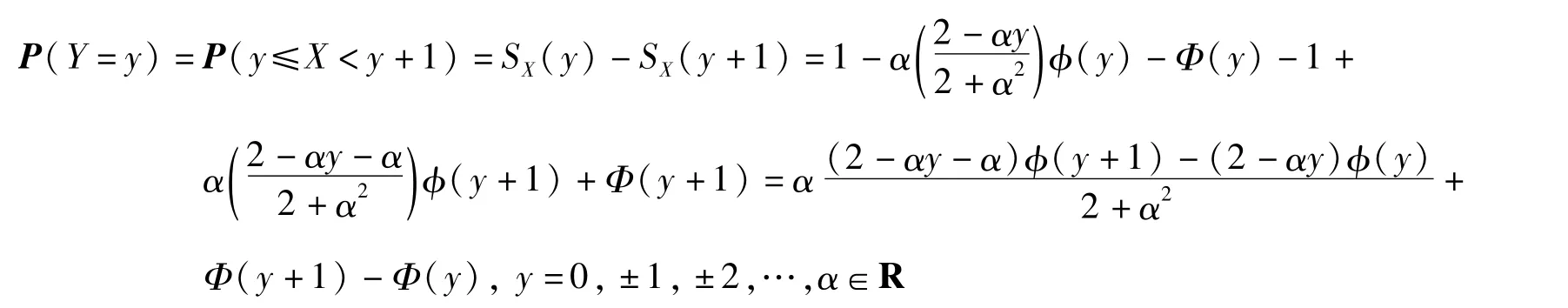
图1展示了3个不同参数值下DASN（α）的概率质量条形图，随着参数α的变化，图形呈现不同的形状。

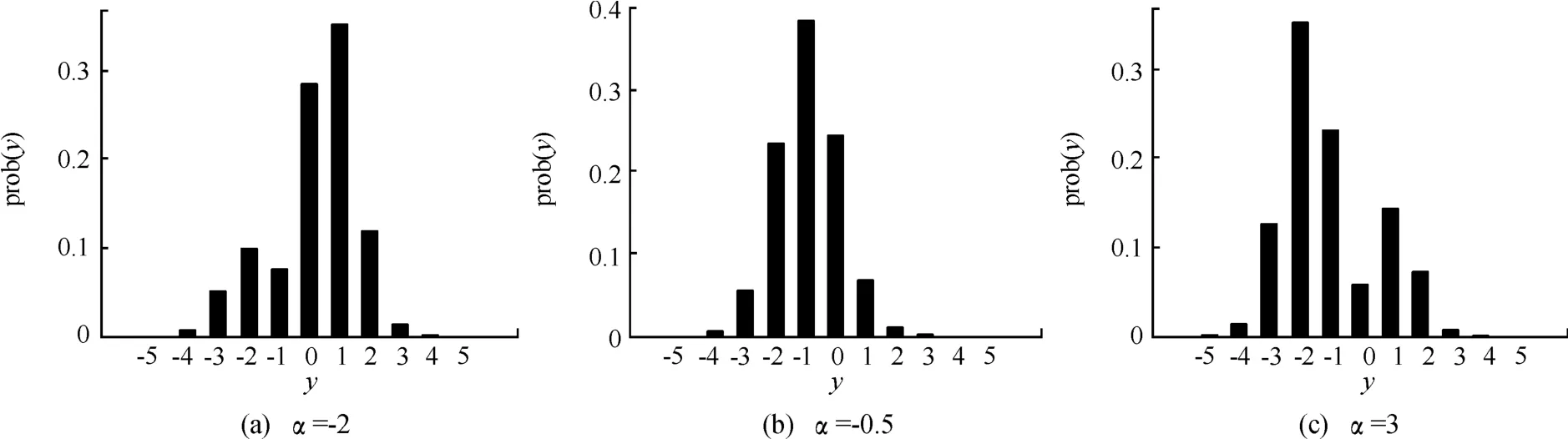
图1 DASN分布在α=-2、0.5、3时的概率质量条形图

注2 若随机变量Y～DASN（α），有

1）Y的概率质量函数有如下递推关系式

2）Y的累计分布函数如下

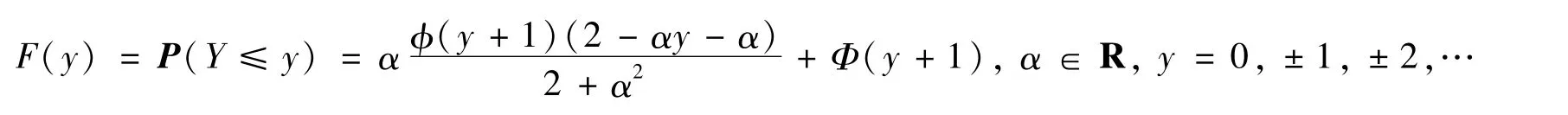
3）当α=0时，那么Y服从离散标准正态分布即Y～DN（0，1），即方程（4）退化为

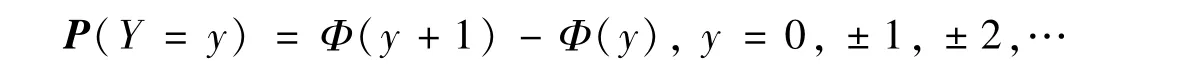
4）当α→±∞时，那么Y服从离散双峰正态分布（关于双峰正态分布详细内容参见文献［1］），记Y～DBN，即等式（4）退化为

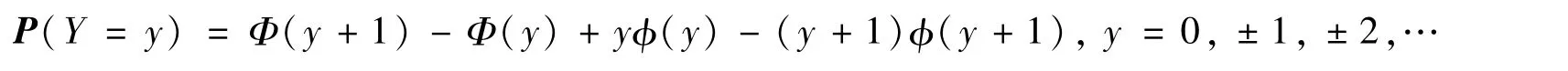
命题1若随机变量Y～DASN（α），那它的高阶矩存在，且为

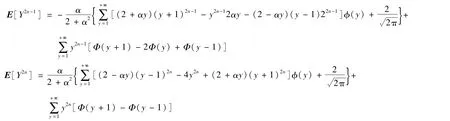
这里α∈R，n∈N+。

注3特别地，当n=1时，分别有

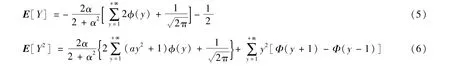
由等式（5）和（6）可得随机变量Y的方差Var［Y］=E［Y2］-（E［Y］）2，此处略。通过比值判别法可知级数是收敛的，因此，对于任意的α∈R，E［Y］和Var［Y］是有界的，应用R软件的DEoptim函数计算出E［Y］和Var［Y］的范围如下

命题2若随机变量Y～DASN（α），有

1）Y的生存函数如下

等式（7）由定义SY（k）=P（Y＞k）=1-F（k-1）即可得出。值得注意的是，DASN（α）的生存函数与ASN（α）的生存函数（2）相同。

2）由等式（7）可得Y的失败率函数为

不同参数值下DASN（α）的失败率函数如图2所示。

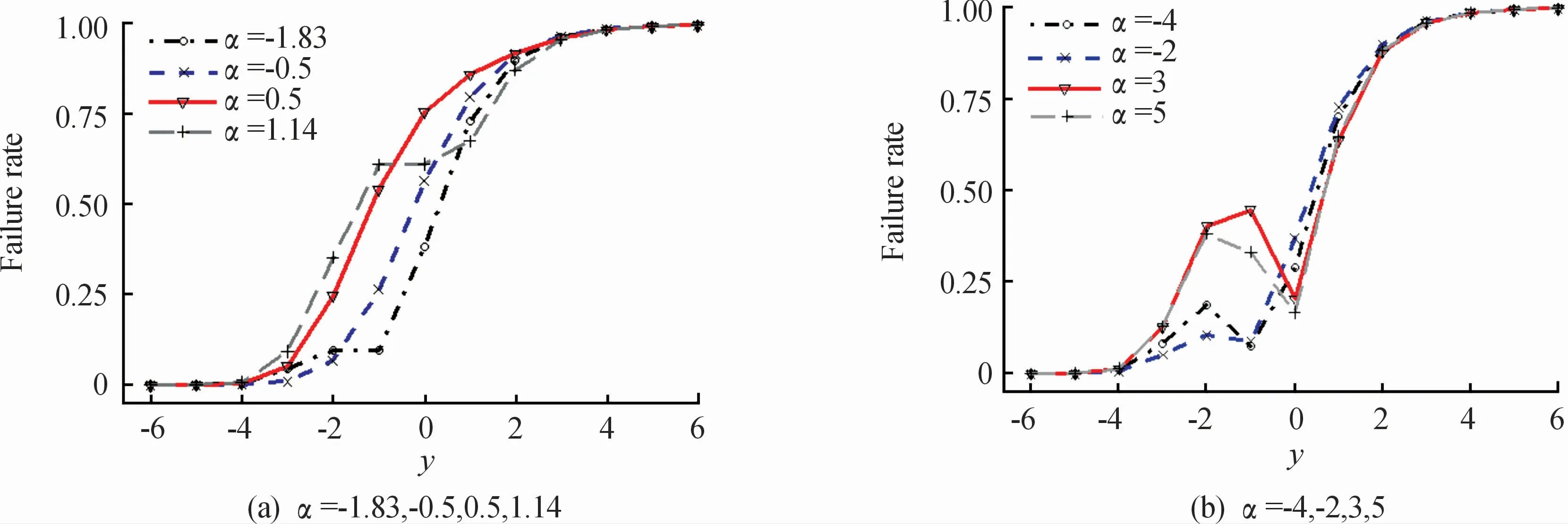
图2 DASN分布的失败率函数曲线

从图2可以看出：随着参数α的取值不同，失败率函数出现不同的形状，借助R软件计算，当α的取值在-1.83～1.14时，失败率呈严格单调递增趋势；当α的取值大于1.14或者小于-1.83时，失败率呈先递增后递减然后再递增的趋势。

由文献［1］可知，若连续随机变量X～ASN（α），令T=μ+σX，这里μ，σ分别为位置和尺度参数，那么T具有如下生存函数

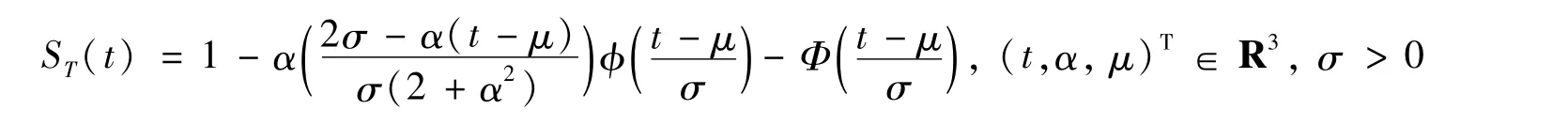
记T～ASN（μ，σ，α）。

定义2若离散随机变量Z=有如下概率质量函数

其中T～ASN（μ，σ，α），m=（z-μ）/σ，z=0，±1，±2，…，（α，μ）T∈R2，σ＞0，称Z～DASN（μ，σ，α）。

注4当μ=0，σ=1时，等式（8）退化为等式（4）。

命题3若随机变量Y～DASN（α），Z～DASN（μ，σ，α），关系式Z=μ+σY成立的充要条件是μ为整数且σ=1。

证明：因为当Z=μ+σY成立时，有

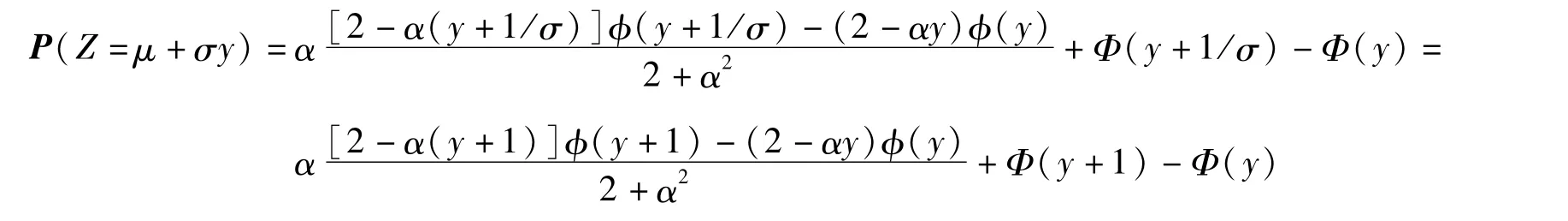
P（Z=μ+σy）=P（Y=y）成立必须满足σ=1，又因为随机变量Y和Z=μ+Y必须是整数，所以μ也是整数，反之也成立。

2 参数估计

2.1 最大似然估计

设Z1、Z2、…、Zn是来自DASN（μ，σ，α）的一个独立同分布简单样本，z1、z2、…、zn是其样本观测值，参数μ、σ和α的对数似然函数为：

式中：mi=（zi-μ）/σ；1≤i≤n。对等式（9）分别关于参数μ、σ和α求导得到对数似然方程组

式中A=α［2-α（mi+1/σ）］φ（mi+1/σ）-α（2-αmi）φ（mi）+（2+α2）［Φ（mi+1/σ）-Φ（mi）］，不能直接得到参数最大似然估计量的显示表达式。然而，借助R软件的DEoptim函数，可给出最大似然估计量的数值解。

2.2 随机模拟

通过求得上述对数似然方程组的近似解，可以得到参数μ、σ和α的最大似然估计值。为了研究参数估计量的优良性，进行随机模拟试验。令α=-3、-1、1、3，位置参数和尺度参数分别设为μ=0，σ=1，样本量依次为30、50、100，模拟重复的次数为1 000。生成离散alpha偏正态分布的随机数步骤如下：

1）考虑连续随机变量X～ASN（α），其分布函数为F（X）。

2）从均匀分布U（0，1）中产生随机数U。

3）计算X=F-1（U），令Y=［X］。

3 实证分析

将DASN（μ，σ，α）对一个来自cBioPortal数据库的癌症数据集进行拟合，借助R软件，得到了参数的最大似然估计值、样本的对数似然值以及AIC和BIC，然后将该分布与离散正态分布以及ASN（μ，σ，α）相比较。

考虑了125例患者首次被诊断出髓母细胞癌时的年龄，样本数据来自2012年。表2展示了各分布的样本对数似然值、AIC和BIC以及参数的最大似然估计值，图3分别展示了的概率质量图和样本数据频率图。

表1 DASN（μ，σ，α）参数最大似然估计量的SD和MSE

表2 125例髓母细胞癌患者首次诊断年龄的最大似然估计值，对数似然值，AIC和BIC

从表2可以得出：DASN（μ，σ，α）的对数似然值要大于ASN（μ，σ，α）的对数似然值，而它的AIC、BIC值要小于ASN（μ，σ，α）的AIC、BIC值，这说明DASN（μ，σ，α）对样本数据的拟合效果要优于ASN（μ，σ，α），同理也优于离散正态分布。

图3 DASN（2.10，9.52，3.07）的概率质量图（a）和125例髓母细胞癌患者的年龄样本数据频率图（b）

4 结论

首次提出了离散alpha偏正态分布，得到了分布的矩、生存函数和失败率函数，同时讨论了一些重要的统计性质，研究了参数的最大似然估计，并进行了随机模拟试验。模拟结果表明：参数最大似然估计量的标准差和均方误差都随着样本量n的增大而减小。最后，通过拟合真实样本数据，发现定义的离散alpha偏正态分布的AIC和BIC值小于经典的alpha偏正态分布相应的值，这表明使用离散alpha偏正态分布拟合整数数据的效果比连续分布alpha偏正态分布更好。然而，是否所有通过等式（3）得到的离散分布在拟合整数数据时的效果都要优于其对应的连续分布，有待进一步研究。

附录

证明命题1

这里