电动汽车电池包底部锥状物冲击下的力学响应分析

黄 芦，兰凤崇，陈吉清

（华南理工大学 a.机械与汽车工程学院；b.广东省汽车工程重点实验室，广州 510640）

电动汽车动力电池包的安全性和可靠性一直是业界普遍关注的热点问题，而动态速度下的底部碰撞是地面碰撞过程中的主要形式，地面冲击物引起的地面撞击会导致电动汽车发生非常严重的火灾事故。但现有文献主要是对锂离子的单体电池的研究，对于锂离子电池包的研究较少。2012年，Sahraei等［1］研究了在小型软包锂电池和圆柱形锂电池的机械导致的短路试验中首次测量的力位移。郑文杰［2］研究了单体方形锂电池的面内压缩性能，找到了短路失效和挤压特性的关联，Thomas等［3］研究了方形锂电池单体在不同动态冲击下的失效模式，并发现2种失效模式，Lamb等［4］研究了圆柱形锂离子电池在极端条件，如针刺、高温下的失效情况，Xia等［5］研究了满电下的锂离子电池在不同加载条件下，对电池变形的影响，Xu等［6］研究了圆柱形锂离子电池的力学强度理论，提出了一种新的电池力学完整性，Xia等［7］首次尝试从地石撞击的角度对圆柱形电池封装方法的动态冲击进行了数值研究，Zhu等［8］从对电池包箱体结构安全的角度分析了几种结构。

现有汽车的电池包中，主要由圆柱形单体电池或方形单体电池组成，且圆柱形锂离子电池研究较多，方形锂离子电池较少。层叠式的方形电池与圆柱形电池相比，优势主要是铝壳较薄，散热性好，电芯极片采用层叠方式，表面平整，电流密度均匀，且极片很薄，使整体电池质量较轻。锂离子电池包在地面冲击时的损伤，现有文献以准静态加载的形式来求解的较多，但从动态冲击的角度来诠释电池包损伤机理和速度的关系的研究较少，这使得我们无法从动态冲击的角度上更清楚地了解电池包的失效形式。

以方形单体锂电池组成的电池包为研究对象，建立精细化电池包的有限元模型，通过模态实验验证了模型的有效性，进一步对该模型在准静态下0.1 mm/s进行垂直加载，确定电池包失效位移和临界力。在此基础上，研究了不同速度对电池包冲击的影响，并与准静态下进行对比，随后对不同参数的冲击物进行研究，提出了一套评价电池包在冲击作用下失效的方法。

1 锂离子动力电池包的建模和验证

1.1 建立动力电池包模型

研究的动力电池包模型如图1所示，动力电池由288块方形磷酸铁锂电池单体组成，单个电池的电压是3.2 V，故电池包总电压为76.8 V，动力电池包长宽高分别为1 006、616和205 mm，总质量115 kg。通过建模得到电池包的CAD模型，在建模时需要对电池包进行简化处理，主要是删除不必要的倒角圆角和细微的工艺孔，忽略温度传感器和电池间的接线，导入到有限元软件HyperMesh中，利用该软件Geometry模块中的Midsurface功能，实现各零部件中面的抽取，然后进行几何清理，但对于排风扇和其他附属件采用质量点的方式分配到对应安装点位置。

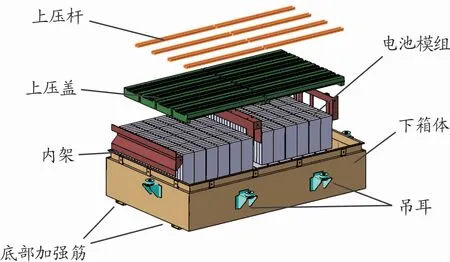
图1 动力电池包模型

1.2 划分网格单元尺寸

划分网格是构建有限元模型的前提，模型的精确性主要由网格质量决定，根据研究问题的不同和几何模型的实际情况选择合理的网格尺寸和单元类型，同时，在满足精度的情况下，控制好网格的数量，尽可能的提高计算效率。动力电池包的箱体主要是由钢板冲压焊接组成，故用四节点四边形单元，同时也有少量三节点三角形单元。动力电池以及其他塑料盖采用四面体实体单元。在选择单元尺寸时，应该根据本身计算机硬件的条件合理选择尺寸大小，以寻求计算结果的准确性和计算时间的最优结果。单体电池如图2中a所示，电芯和壳体为4 mm，为了在电池组的整体模型下获得较好的计算效率，对其力学行为进行了均匀化描述，并在全局模型水平上定义了电池的无断裂行为。

在对电池组件进行实验研究的基础上［9-10］，选择了一种高强度钢的弹塑性性能和各向同性Von Mises模型来表征壳体，壳体内的电芯在压缩过程中具有体积压缩性，在大压缩阶段反应力突然上升，与某些金属泡沫材料的行为接近。选用LSDYNA中的一个与压力有关的可压碎泡沫模型mat63来表征电芯的均匀化特性。电池包有限元模型如图2（b）所示，电池包其他尺寸：整体壳单元为10 mm，一些较小部件如上压杆、内架、前压杆为4 mm。动力电池包的箱体为薄壁结构，选用壳单元，可以大幅度缩短计算机计算时间，提高效率。

图2 有限元模型

另外电池包各部件材料参数如表1所示。

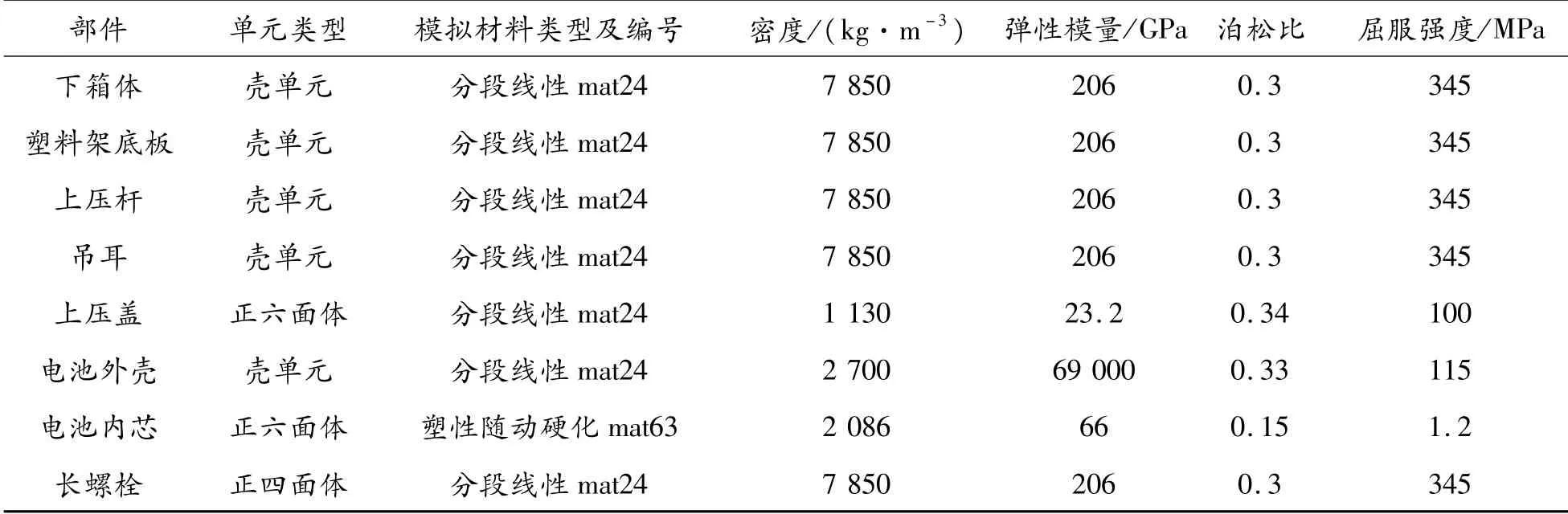
表1 电池包各部件材料参数

在划分动力电池包网格时要依据单元质量标准来控制整体的网格质量，有限元网格质量的规范对最终仿真结果的可信度有直接影响，故在划分网格时必须符合表2的单元质量指标，其中对于六面体和四面体网格的雅克比值可以放宽至0.5，有些不符合单元质量标准的结构，需要重新进行单元网格划分。最终研究的动力电池包有限元模型共有364 134个单元，其中实体单元117 113个，节点300 585个，三角形单元750个，占单元总数的0.1%，远远小于推荐标准5%，能很好地确保网格连续性，保证仿真计算结果精确度。单元雅克比值均大于0.6，且小于0.7的只有443个，仅占电池包有限元模型总数的0.12%，符合单元质量标准。

表2 单元质量指标

1.3 部件连接

动力电池包以焊接和螺栓紧固的连接方式为主，在单元中新建一个component来存放刚性体单元，用1D面板中的Rigid刚性连接功能来模拟焊接，在使用Rigid单元模拟焊点时，通常采用刚度较大的部件的节点作为主节点，同时约束从节点的6个自由度。下箱体内支架和底部焊接在一起，上箱盖和下箱体采用螺栓连接，电池上压杆用螺栓将电池组和塑料架底板紧固在一起，电池包的内架和压杆采用螺栓连接，螺栓用四面体单元模拟。

1.4 模态验证动力电池模型

模态实验有2种，分别为力锤激励法和激振器激励法，研究的电池包由于质量和刚度较大，且各材料组成成分较多，具有非线性特征，故采用激振器激励法。如图3中所示，实验仪器主要包括：电脑、采集动态信号的采集仪、三向加速度传感器、激振器和对应的力传感器、功率放大器、给激振器供电的电荷适调器。实验共布置了120个测点，用以描绘出电池包内外部的主要轮廓，将激振器在一固定位置对电池包进行持续激励，在多处测量频响信号，采集频率的分辨率为0.5 Hz。通过LMSTest.Lab将得到的激振力信号和加速度响应进行傅里叶变换得到最后的拟合频率响应函数，得到频率响应函数后进行模态参数识别，即需要的模态频率和振型。

图3 模态实验装置

仿真时的边界条件，按照真实情况约束电池包各个吊耳的6个自由度，求解出电池包前4阶模态的固有频率和振型，将电池包自由模态下的实验和仿真结果进行对比分析，如表3所示，固有频率的误差在5%以内且振型如图4所示，仿真结果的振型和实验结果振型一致，验证了电池包模型的正确性。

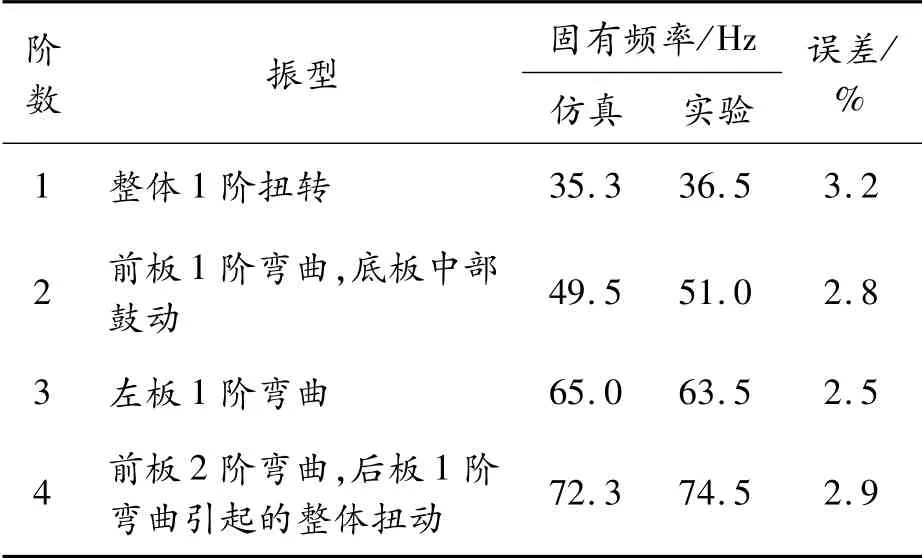
表3 模态实验与仿真结果

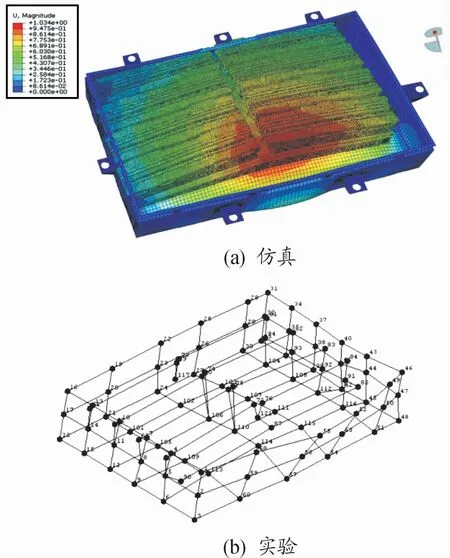
图4 电池包模态仿真与实验结果（4阶）

2 电池包在准静态加载下的响应

2.1 理论基础

地面冲击在地面碰撞时被模拟为一个被一个半径为Rb的半球形冲头冲击的圆板的局部压痕。Simonsen等［11-13］导出了这个加压过程的解析解，Lee等［14］对这个结果进一步分析研究。本文直接引用Simonsen的最终结果，垂直加载一直进行到失效，涉及到大挠度，其中下箱体是主要的抗负荷机制。如图5所示，刚性球头以1 mm/s的速度垂直加载于厚度为h的薄板上，作用力为P，表示在直角坐标系X-Y中，X方向表示板的半径方向，Y方向表示垂直加载的方向。任意取球头与薄板接触上的一点记为K点，则K点的坐标为Xk和Yk，在以顶端半径为Rb的冲头作用于薄板上时，薄板向上发生变形成为一个圆盘，圆盘半径R0，即撞击点到受影响模块最近边界的距离为R0，K点到冲头中心与垂直加载方向形成的弯曲角为ψk，冲头上升的位移为δ。

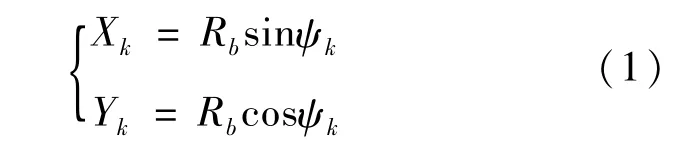
式中：Rb是冲头的顶端半径；ψk表示弯曲角。

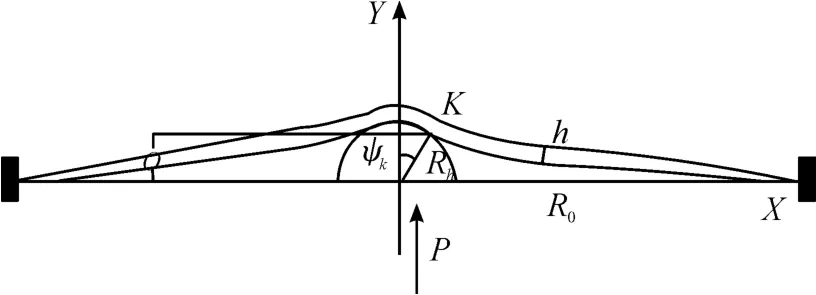
图5 准静态加载的模型示意图

总阻力P与冲头位移δ之间的关系以参数形式给出

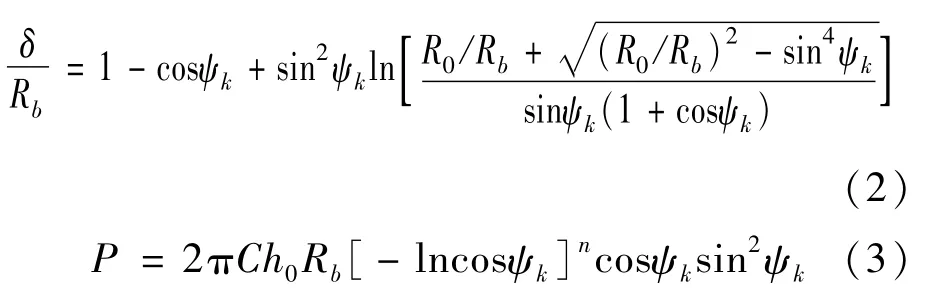
式中：C为薄板材料的强化系数。

根据稳定性理论［15］，当抵抗力达到最大值时，板的承载能力被耗尽，发生破裂，此时弯曲角ψkr有如下关系

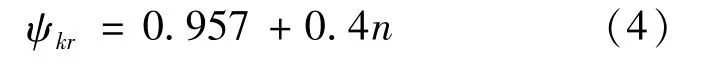
式中：n为薄板材料应变硬化指数。

最终下箱体在垂直载荷加载下的临界位移σf和力Pf关系为

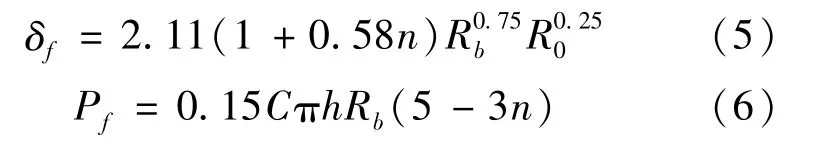
2.2 电池包在准静态作用下的响应

电池包下箱体材料为6061铝合金，厚度h为3 mm，道路碎片形状各异，采用三角锥的模型［15］来模拟地面冲击物，对整体电池组进行了准静态冲孔。在LS-DYNA中将碰撞物体简化为一个锥台刚体，如图6所示。碰撞物顶端半径Rb=10 mm，圆锥顶角β=45°，在垂直加载下得到了如图7的力位移曲线，并标记了1-5的位置点定义了电池组组件不同部件的断裂过程顺序。分别为下箱体、塑料架底板、电池外壳、电芯、上压盖，当下箱体刚穿孔时，力-位移曲线出现第1个峰值。在随后的冲头推动下断裂，并且沿下箱体上穿孔周围的径向裂纹扩展，而对冲头的阻力立即下降。冲头在第1个力峰值处的压痕位移约为58 mm。根据式（5）和R0为300 mm（模拟中钢板较短边缘长度的一半），失效位移的理论解为61 mm，与精确数值解非常接近。

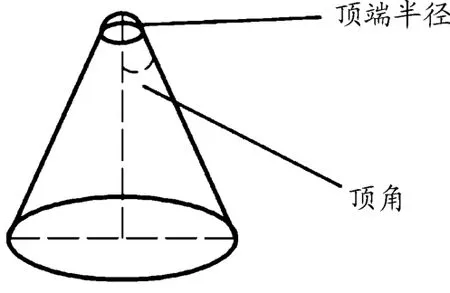
图6 锥台刚体

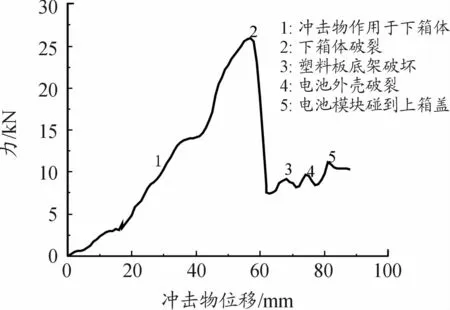
图7 准静态下动力电池包的力-位移曲线

图8 具体展示出了冲击物碰撞电池包的侵入过程，每个框架对应于图7中的标记号。在位置1时，冲击物碰到下箱体，且随着位移的增大，力也在不断增大，当位移达到58 mm时，此时出现第1个力降为位置2，在压痕过程中，下箱体在冲压区首先发生断裂。裂纹扩展沿着冲头尖端的径向传播，并留下一个孔。冲孔物体的进一步凹陷扩大了穿孔的直径，并使塑料架底板破裂，形成第2个力降位置3，变形更加集中在冲头尖端正上方的区域。冲击物继续上升，电池模块外壳变形，在压痕过程中，冲头上方的单个电池单元被向上推，在位移达到75 mm时，电池外壳破裂，形成第3个力降位置4。在电池模块上升抵到上压盖时，到达位置5，此时并没有穿破上箱盖；在下箱体断裂前，下箱体的挠度覆盖面积较大，冲孔载荷在下箱体上的传递更为均匀，相对较多的单元受其向上运动的影响。下箱体被刺穿后，下箱体的偏转集中在刺穿孔的边缘，同时，向上移动的电池推动上压盖。上压盖提供了阻力，冲头尖端逐渐集中的压痕和地板的阻力导致冲头正上方的单元压缩和缩短。从图8的位置5还可以注意到，向上移动的电池单元最终没有刺穿箱盖。

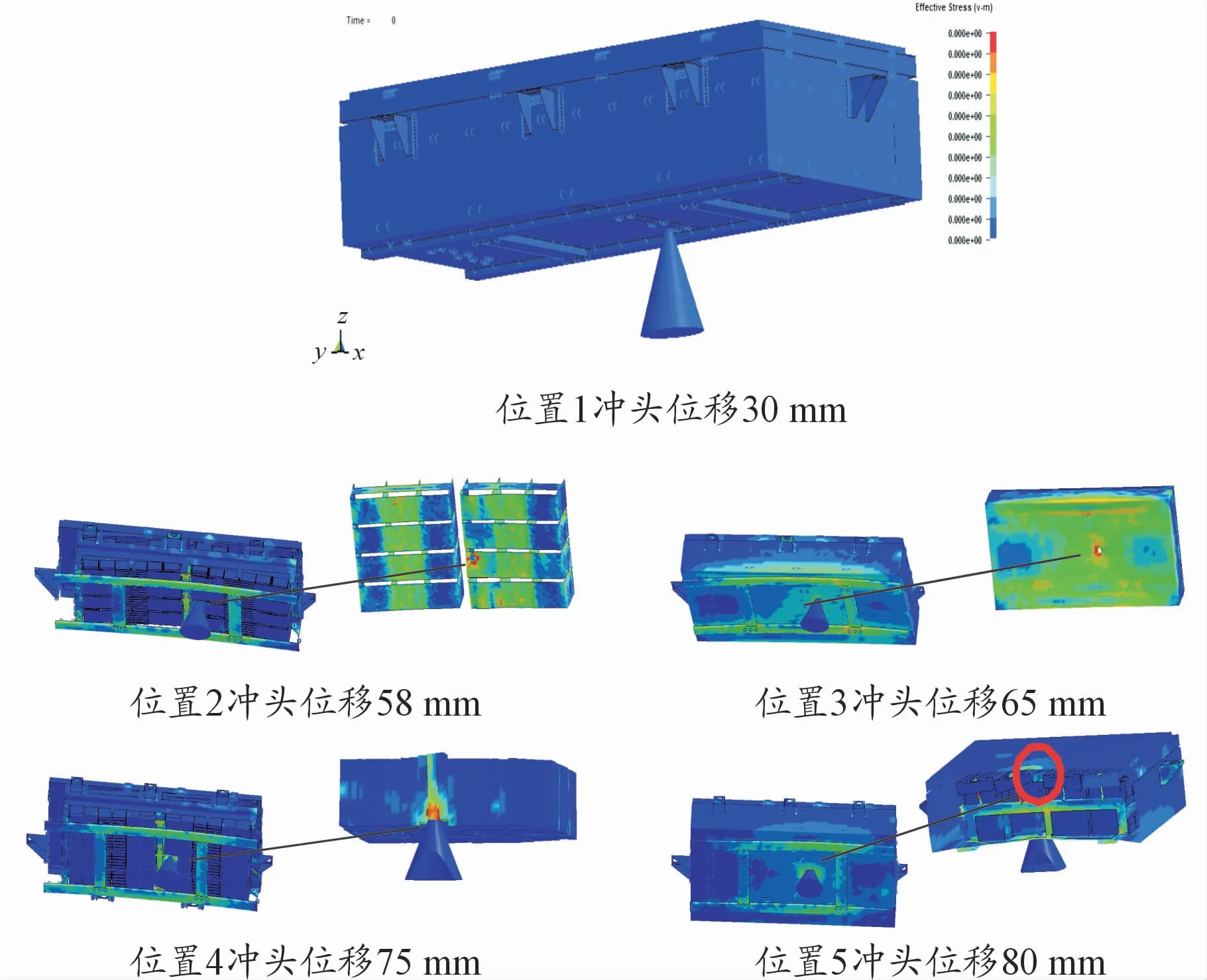
图8 冲击物碰撞电池包的侵入过程

在全局模型阶段，电池失效不包括在模型中。图9展示出了电池模组的失效行为，在图中可以更清楚地区分电池单元变形的5个不同阶段。在第1阶段，电池上升位移随着冲击物侵入位移的增大而增大，此时下箱体还未被穿破；在第2阶段，当侵入位移达到58 mm时，下箱体破裂，但此时电池的侵入位移还在上升；到达第3阶段，冲击物侵入位移65 mm，塑料架底板被穿破，电池此时上升位移达到最大；随着冲击物的继续侵入，在第4阶段，冲击物直接撞上电池模组，导致电池在很小的凹痕距离内开始急剧缩短，应力集中。随着电池高度的继续上升，外壳下端出现局部屈曲和折叠，电池的局部塑性变形严重集中。在冲压点达到第5阶段，电池抵到上压盖，电池向上运动的阻力被部分释放，冲头上方的电池被卸下。在此阶段，电池的弹性变形得到恢复。

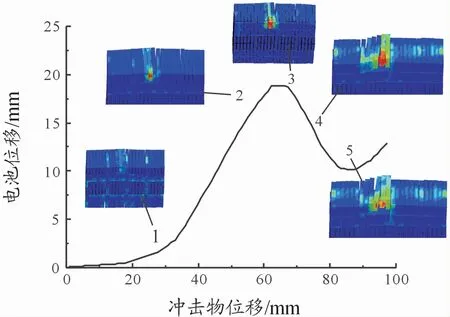
图9 电池模组的失效行为

实际上，如式（5）所述，地面撞击中可能达到的最大穿透量取决于道路碎片的几何形状。

3 动力电池包在不同参数的冲击物的数值模拟结果

3.1 电池包在不同速度冲击作用下的响应

在准静态解中，以0.1 mm/s的速度对电池包进行加载，参数是冲头的位移δ。然而在真实情况中，地面碰撞发生时，冲击物都是以不同速度撞向电池包的。在动态碰撞的情况下，分别以不同速度进行加载，过程参数是时间。在冲击物为顶端半径Rb=10 mm，圆锥顶角β=45°下，分别以1～5 m/s冲击下箱体，在同一位置对底部进行碰撞，仿真分析了0.1 s内的碰撞响应（如图10为1～5 m/s力与位移的关系），并与准静态下的响应比较。

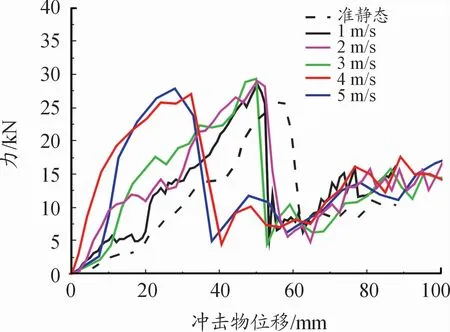
图10 不同速度冲击电池包的力与位移曲线

从图10可以看出，在不同速度的冲击下，电池包的失效位移也不同，相比于准静态下的失效位移58 mm，动态冲击下的失效位移要更小，且随着速度的增大而减小，1～5 m/s碰撞下的失效位移为准静态下的90%～50%，临界力相比于准静态下的临界力增大了5%～10%。为了进一步探究高速下的冲击影响，研究了10～30 m/s碰撞下的响应，这在很大程度上涵盖了车辆碰撞时的速度范围，如图11高速冲击电池包的力与位移曲线，也证实了高速碰撞下失效位移远小于准静态下的失效位移。

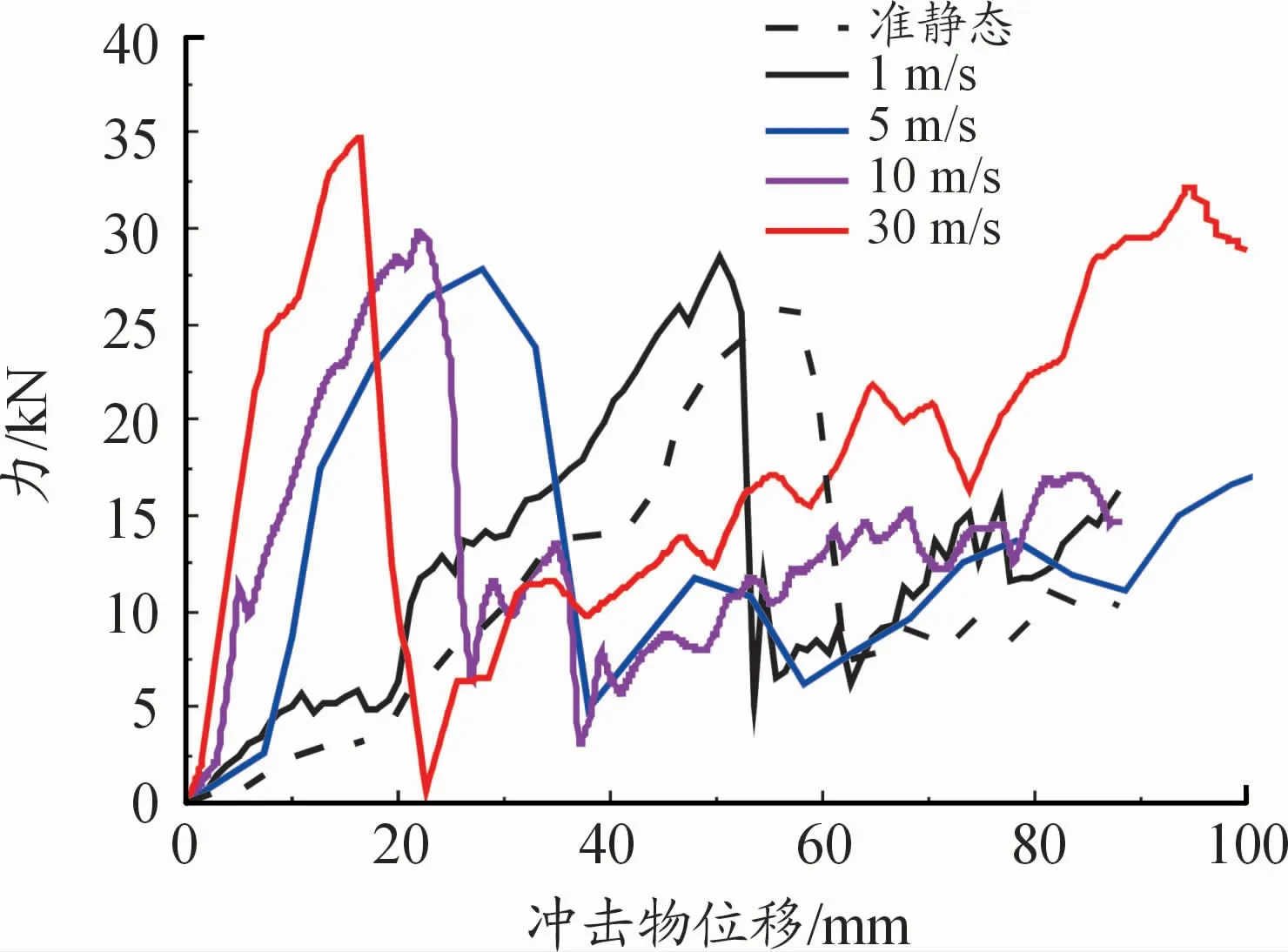
图11 高速冲击电池包的力与位移曲线

临界失效位移与速度拟合曲线如图12所示，结果显示电池包的失效位移与速度成负相关，用准静态加载的方式来评价电池包在地面碰撞的失效位移，显然不太准确。

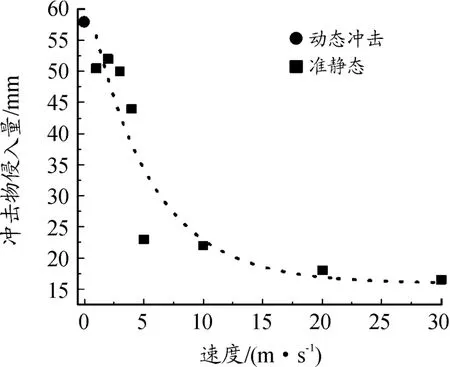
图12 临界失效位移与速度拟合曲线

采用最小二乘拟合方式，临界失效力与速度拟合曲线如图13所示，可以看出所需最大的临界力随速度成正相关，随着速度的增大所需要的临界力增大。

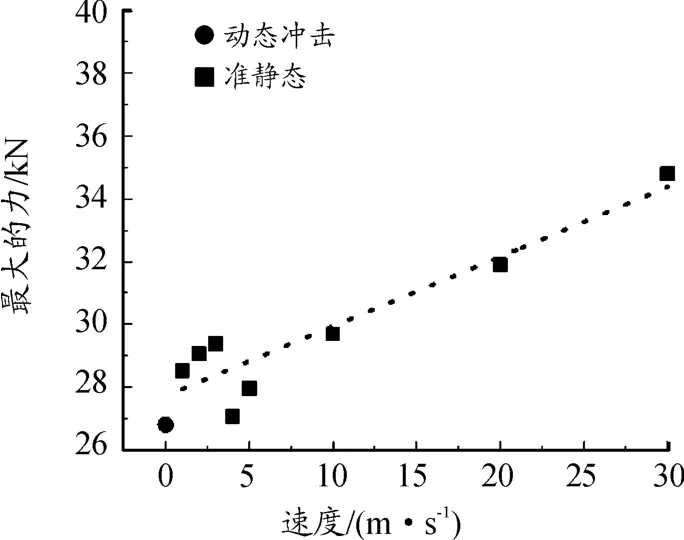
图13 临界失效力与速度拟合曲线

3.2 电池包在不同顶角角度冲击作用下受到的影响

电池包的破坏程度也取决于道路碎片的尖端几何形状，不同冲击物顶角在碰撞电池包所造成的撞击点到受影响模块最近边界的距离R0不同。采用顶角依次为45、90、135°的冲击物在1 m/s下对电池包进行动态冲击。

从图14可以看出，在顶角为45、90°的尖锐顶角时，力都在冲击物侵入52 mm左右发生突降，此时下箱体发生破裂，且破裂时90°的冲击物所造成的破损力最大值略大，但135°冲击物并没有发生力的突降，没有造成下箱体破损。图15也给出了在碰撞末了的位置图，但是这并不意味者对电池模组没有损伤，图16在冲击物侵入为52 mm时，45、90°顶角所造成的电池上升量为18 mm，但135°时电池的上升量却最高，达到了25 mm。随着顶角的增大，电池侵入量的斜率变大，即更容易被破坏。尖锐冲头在相同速度碰撞时，对于电池包整体所造成的损伤和顶角关系较小。

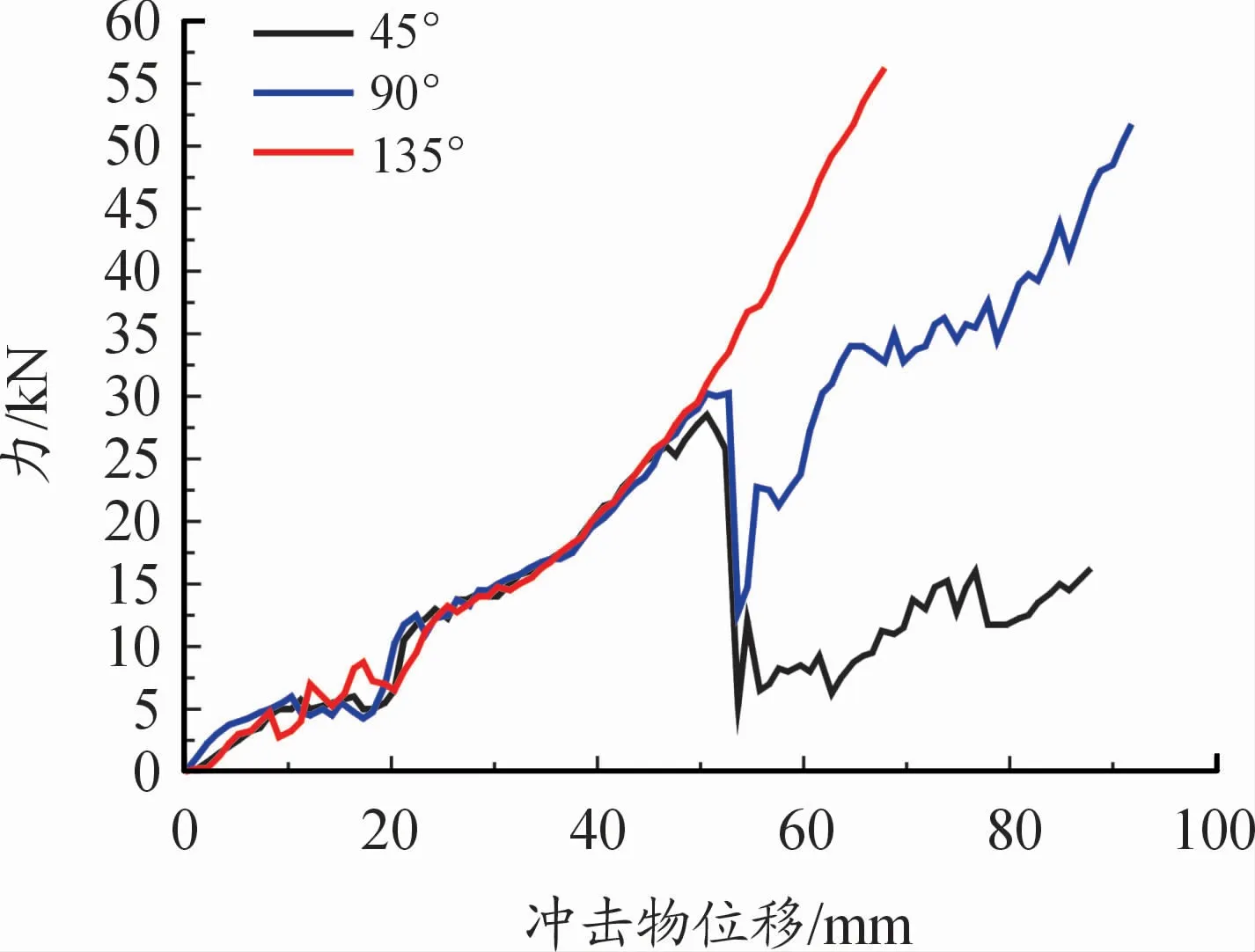
图14 不同圆锥顶角的力位移曲线

在顶角为135°的冲击物碰撞时底端虽然没有破裂，但是电池包的电池模组侵入量已经远远超过尖锐冲头所造成的损伤。这与钝头冲头的顶角所造成的撞击点到受影响模块最近边界的距离R0密切相关，其原因是钝头压入过程中，接触面积较大，抵抗力也变大，同时，相邻电池单元数量相对较多，其变形也分担了一部分抗力，使之最后还没有穿破下箱体。

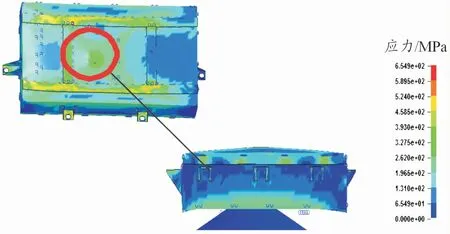
图15 135°顶角在0.1 s时的碰撞示意图

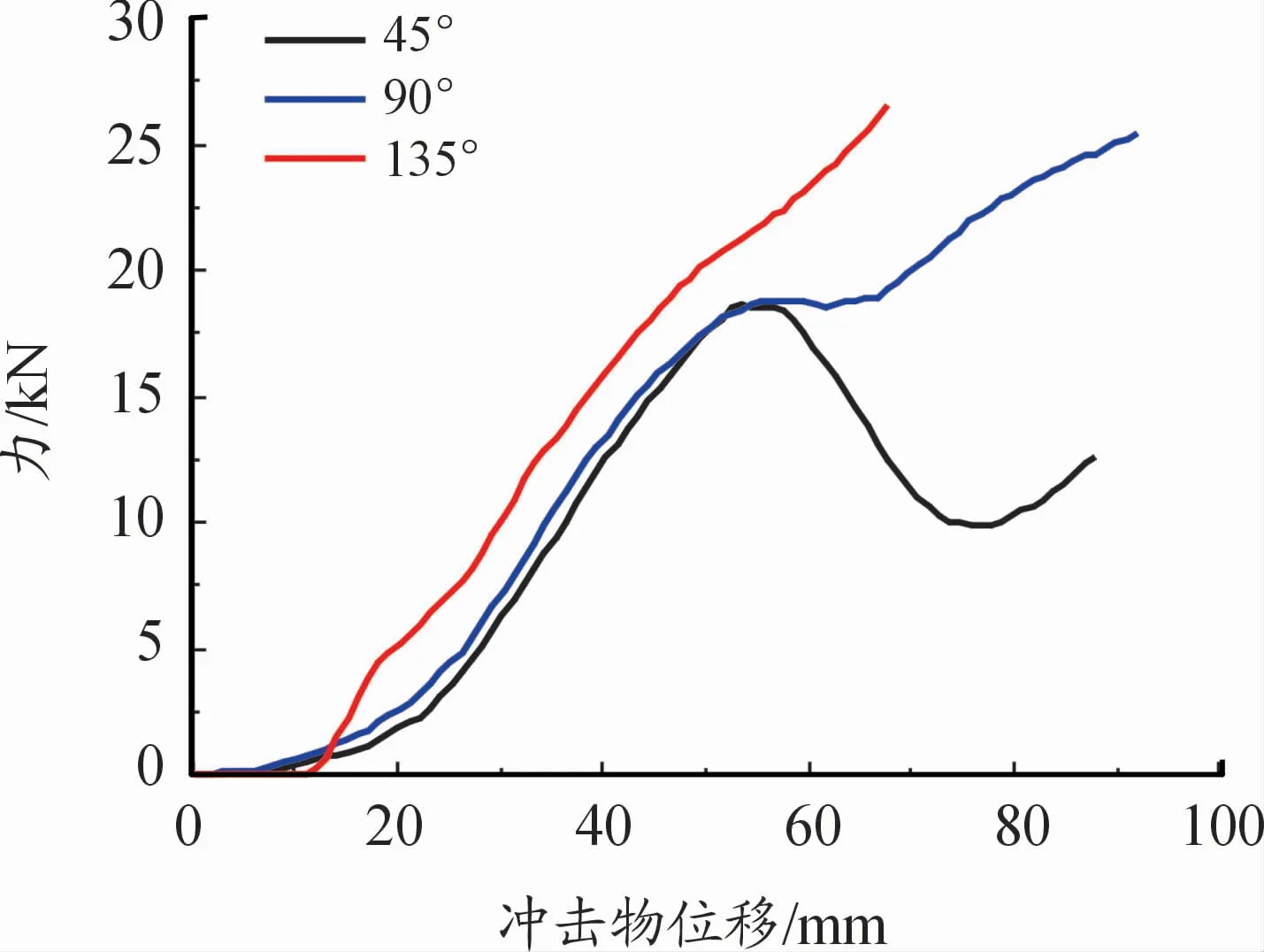
图16 不同圆锥顶角的电池侵入位移和冲击物位移曲线

3.3 电池包在不同顶端半径冲击作用下受到的影响

在速度为1 m/s、顶角为90°、顶端半径分别为10、20 mm的冲击物碰撞下，不同顶端半径的力和位移曲线如图17所示。顶角半径不同时下箱体破裂时的最大力以及电池位移量也不同，在顶端半径为10 mm时，当冲击物侵入量达到52 mm时，力曲线此时急剧下降为30 kN，表明此时下箱体发生破裂，此时图18电池的位移量达到了18 mm；而在顶端半径为20 mm时，力在45 kN时发生突变，此时冲击物位移为60 mm，电池上升量为22 mm，如图18所示，可以看出这2条曲线斜率基本一致，但由于顶端半径的不同，导致最终结果相差很大，表明不同顶端半径的冲击物，对于电池包的失效位移影响较大，且随着顶端半径的增大，冲击物需要更大的侵入量才能穿破电池包，即顶端半径更小的冲击物碰撞电池包时，更容易造成电池包的破裂。

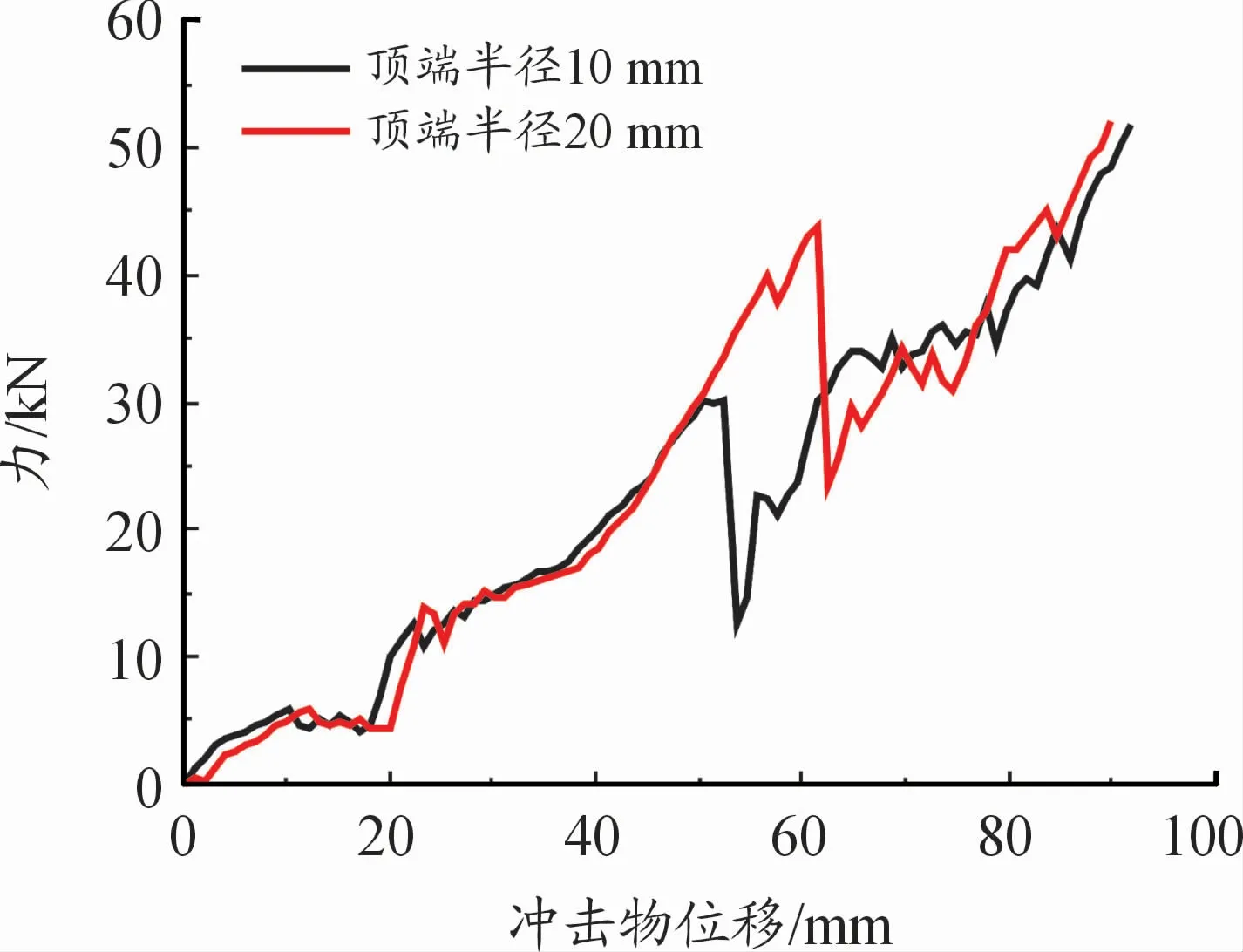
图17 不同顶端半径的力和位移曲线

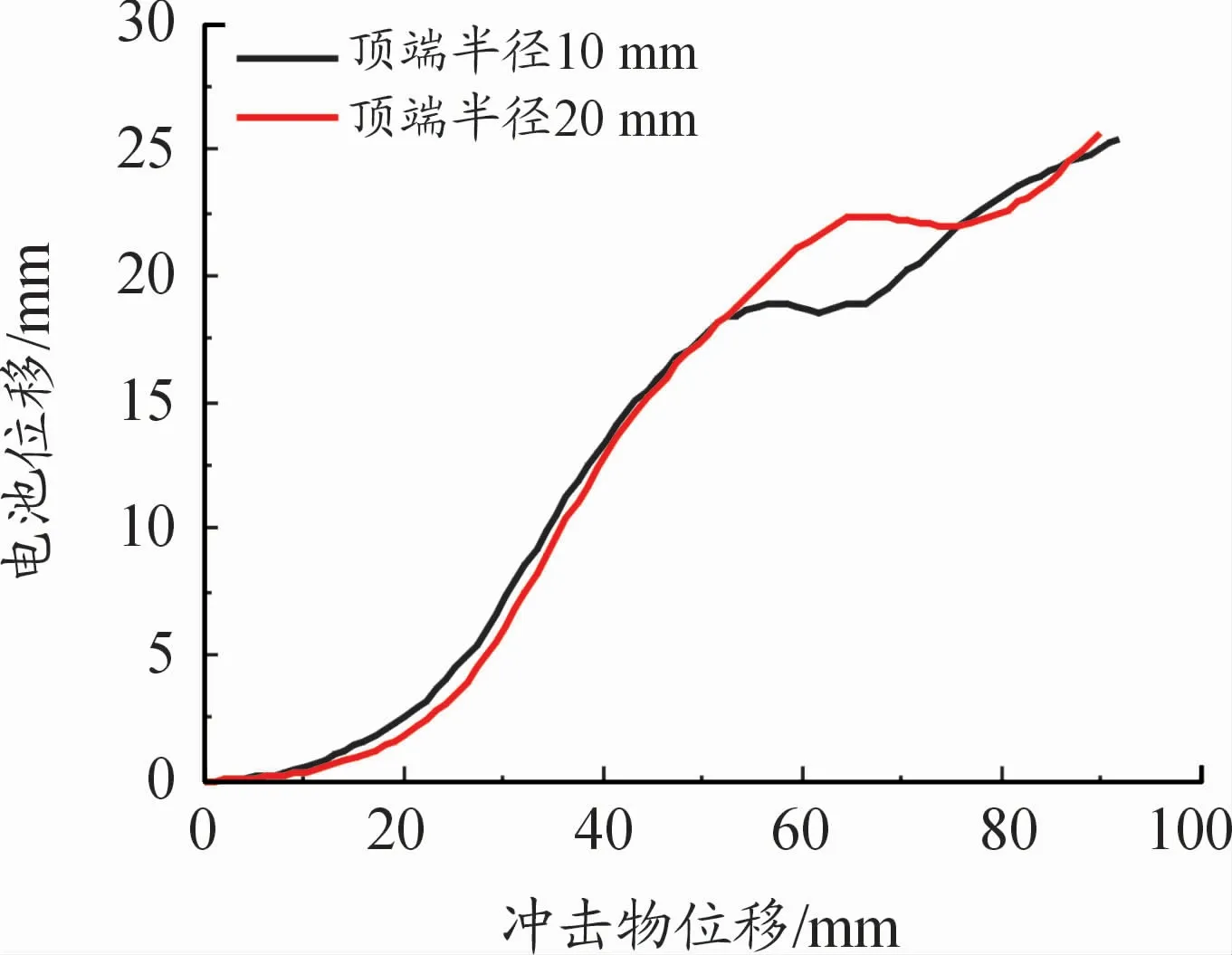
图18 不同顶端半径的电池侵入位移和冲击物位移曲线

4 结论

1）在准静态以0.1 mm/s的速度加载冲压电池包时，电池包在冲击物侵入量达到58 mm时，下箱体发生破裂，临界力达到了25 kN。

2）动力电池包在与道路碎片发生动态碰撞时，随着速度的增大，失效位移不断变小，当碰撞速度为1～5 m/s时，失效位移为准静态失效位移的90%～50%；随着速度的增大，失效的临界力在增大，失效临界力为准静态下临界力的5%～10%。动力电池包在地面碰撞时以准静态下的失效位移和力来评价电池包的失效行为是不准确的，应该以动态冲击下的真实情况来评价。

3）不同顶角的冲击物与电池包发生碰撞时，失效位移和顶角无关，但是当顶角过大时，会导致整体的电池组上升位移大大增加，随着顶角的增大，电池侵入量的斜率也增大，这些以更高的速度硬化，导致整个电池包存在危险。

4）不同顶端半径的冲击物碰撞电池包时，随着顶端半径的变大，失效位移和临界力均变大，顶端半径更小的冲击物，穿破电池包所需的失效位移和临界力更小，对电池包威胁更大。