基于自适应Backstepping的分布式驱动电动汽车容错控制

朱 燕，姚雪莲，贝绍轶，杨 艺，丁东东

（江苏理工学院 汽车与交通工程学院，江苏 常州 223001）

与传统汽车相比，分布式驱动电动汽车具有车轮可独立控制、响应速度快等优点［1］，其控制问题受到越来越多的关注。郑子骜［2］使用Backstepping积分法、滑模控制法等对汽车进行轨迹控制以提高电动汽车的稳定性。部分文献对汽车控制设计中大多没有考虑汽车可能发生的执行器故障问题。随着系统复杂度的增加，电动汽车执行器和传感器的故障概率也相应增加，导致车身可能会出现非期望的车速、横摆角速度、输出力矩不协调等问题，从而使驱动电动汽车行驶安全性能下降［3-5］。一旦车辆驱动系统出现故障，上述这些方法不适用于解决不确定故障情况下的控制问题。

容错控制在保证系统安全性、可靠性方面有着重要的作用［6-7］。分布式驱动电动汽车容错控制的主要目标是在驱动电机发生故障时保持期望的车辆性能。针对电动汽车执行器故障下的控制问题，MUTOH N等［8］采用切断故障电机动力输出的方法，使车辆在发生失效故障的情况下仍能运作。褚文博等［9］给出的协调控制方法，提高了车辆在驱动器失效故障下的动力性和稳定性。刘杰等［10］提出一种转矩分配策略来抑制驱动电机失效等造成的驱动力下降问题。WANG R等［11］采用基于自适应的被动容错控制和主动故障诊断的方法解决车辆执行器故障问题，保证执行器故障时的安全性。然而上述方法未考虑车辆系统行车过程中执行器故障的不确定性，不确定故障情况下的电动汽车系统的渐近跟踪控制将更具有挑战性。LIU G H等［12］采用滑模控制来解决不确定执行器故障情况下的跟踪协调控制问题，提高了输出跟踪的精度，但只解决了执行器卡死故障。然而，汽车在实际运行过程中，可能存在各种执行器故障情况，且它们发生的时间、类型以及故障值都是未知的。

以分布式驱动电动汽车为研究对象，考虑作为主要执行器的驱动电机故障的不确定性问题，针对车辆的队列保持和轨迹跟踪问题进行了容错控制方法的研究。建立带有执行器故障的3自由度模型以及车辆排列、轨迹跟踪的控制目标模型，运用Backstepping法设计理想的控制信号，引入故障指示函数设计各故障模式下理想的故障补偿控制器，将各故障模式下理想的控制器进行融合得综合补偿控制器。设计自适应律，对执行器故障参数、综合控制器参数进行估计。基于李雅普诺夫稳定性理论，证明了当车辆系统发生不确定故障时，本文设计的Backstepping自适应控制器能够保证车辆闭环系统稳定以及渐近跟踪给定的输出指令。

1 系统描述

1.1 车辆模型

车辆模型如图1所示。选用3自由度模型，不考虑空气阻力。

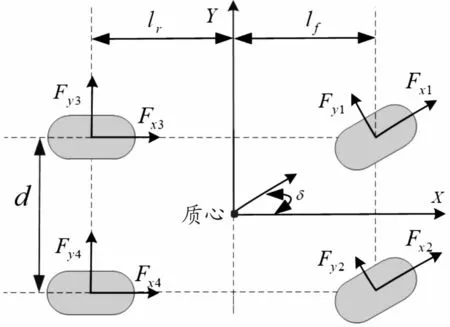
图1 车辆模型示意图

车辆动力学方程为［12］

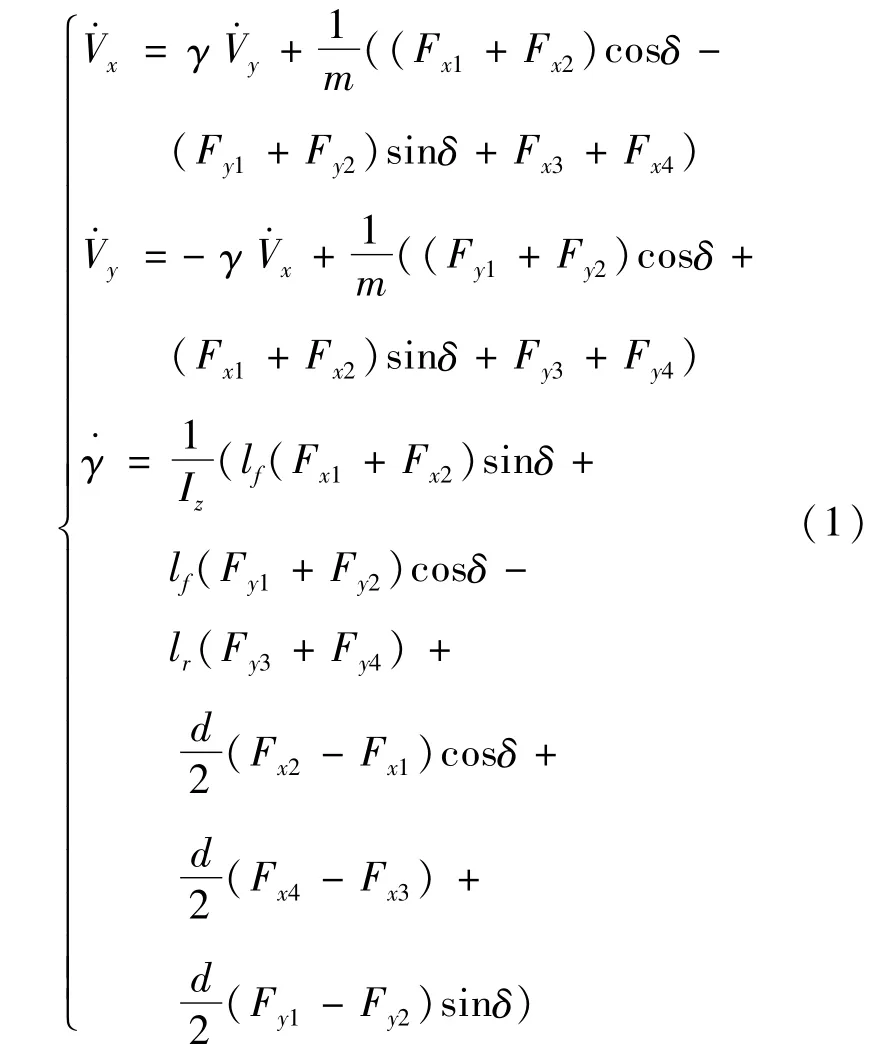
式中：m为车辆质量；Vx和Vy表示车辆的纵向速度和侧向速度；γ为车辆的横摆角速度；Iz为横摆转动惯量；lf、lr为质心到前后轴的距离；d为车辆轮距；δ为转向轮的转角；Fxi为驱动轮受到的纵向力；Fyi为驱动轮受到的侧向力，下标i=1，2，3，4表示各个车轮，文中其他部分定义相同。

本文使用魔术轮胎公式表示各轮受到地面的侧向反力，其形式为

式中：X为车轮的侧偏角；D、C、B、E为拟合系数。

对车轮回转进行受力分析，忽略滚动阻力的影响，其动力学方程为

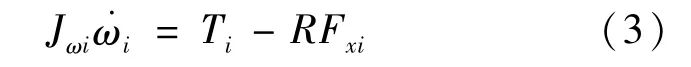
式中：Jωi为4个车轮的转动惯量；ωi为4个车轮的旋转角速度；Ti为驱动电机产生的驱动力矩；R为车轮的有效半径；Fxi为地面对轮胎的纵向力。

1.2 车辆控制目标模型

车辆控制目标模型如图2所示［13］，分别为车辆排列和车道跟踪模型。其动力学方程为

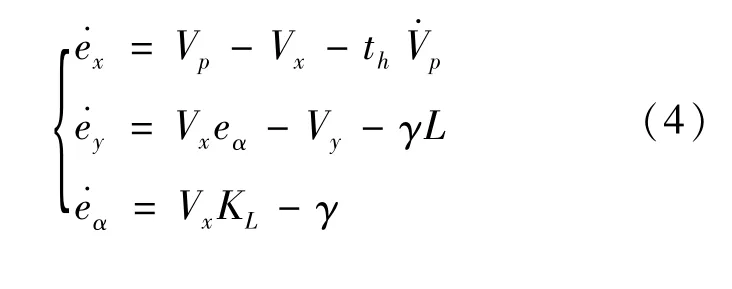
式中：ex=（xp-x）-xspacing，xp为前车所在的纵向位置，x为车辆的纵向位置，xspacing为理想的车间距离，ey为车辆当前位置和参考轨迹之间的侧向距离偏差，eα为参考轨迹切向方向与车辆纵向行驶方向之间的角度偏差，Vp为前车速度，th为车辆与前车之间的时间差，L为沿着车辆行进方向的前视距离，KL为参考轨迹的曲率。

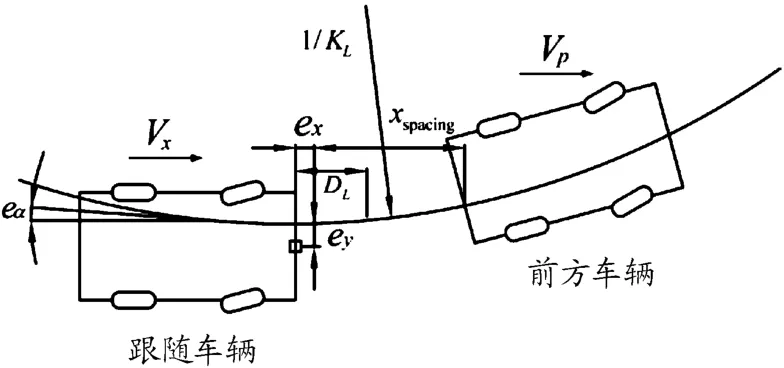
图2 车辆排列和车道跟踪模型示意图

2 问题描述

定义状态向量x1=［ex，ey，eα］T，x2=［Vx，Vy，γ］T，控制向量u=［u1，u2，u3，u4］T=［T1，T2，T3，T4］T为车辆的4个电机输出力矩。系统模型（1）～（4）可以表述为

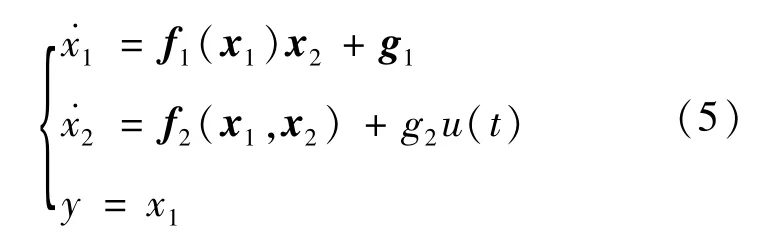
驱动电动汽车可能会发生电机卡死或者完全失效故障［12］：为轮内电机卡死后产生的常值信号。执行器产生的故障也可能是时变的，实际行车情况可以选取正弦函数描述时变故障：为未知常数。结合2种常见的故障类型，给出一种能够同时处理常值故障和时变故障的复合故障模型，设故障输入为，综合故障模型为

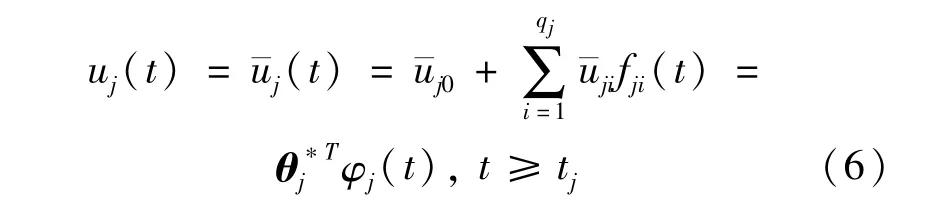
式中：fji（t）（i=2，3，…，qj）为时变函数，为未知故障参数向量，φj（t）=［1，fj1（t），…，fjqj（t）］T∈Rqj+1为已知基函数。

车辆系统故障情况下的输入信号为

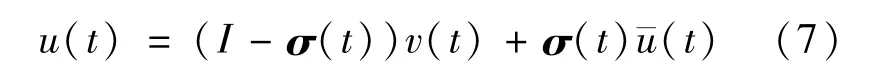
式中：σ（t）=diag｛σ1（t），σ2（t），σ3（t），σ4（t）｝为执行器故障模式矩阵，矩阵分量取值为0或1，分别表示某一个执行器无故障或发生故障。v（t）为待设计的反馈控制输入信号。

本文的控制器设计仅讨论单个执行器故障下的容错控制。考虑以下3种故障情况：①执行器无故障：ui（t）=vi（t），i=1，2，3，4；②执行器1故障：，i=2，3，4；③执行器4故障：，i=1，2，3。其他单个或者多个执行器故障情况设计过程类似。

本文的控制目标是针对电动汽车控制系统发生单个执行器未知故障情况下的队列保持和轨迹跟踪问题，设计自适应反馈控制信号v（t），使车辆闭环系统稳定的同时实现跟踪误差趋近于零。

3 故障补偿控制设计

采用Backstepping控制和自适应控制相结合的方法对未知故障进行容错控制。

3.1 Backstepping控制设计

定义第一个子系统和第二个子系统误差分别为z1=x1-ym，z2=x2-α1，ym为参考输出，α1为待设计的函数。

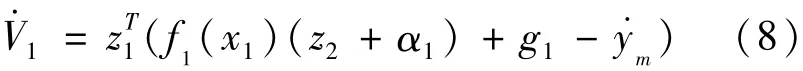
将x2视为中间变量，函数α1选取为

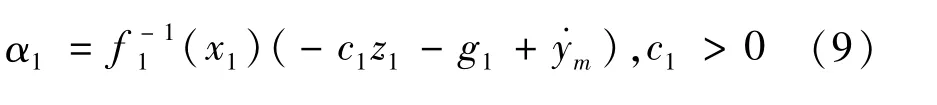
式中：c1为控制器设计的参数，将式（9）代入式（8）中，得到

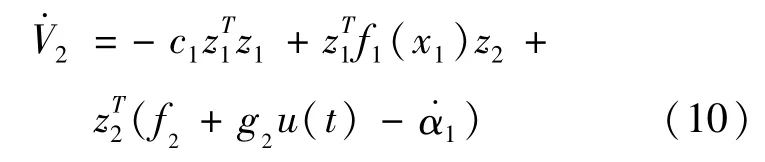
得到理想的控制信号ud（t）为

式中：c2为控制器设计的参数，式（11）代入式（10）中，得到，说明系统实现了期望的控制目标，保证无故障情况下车辆系统稳定和渐近跟踪性能。

3.2 故障补偿设计

针对3种故障情况，即驱动电机全部正常工作、左前电机发生故障、右后电机发生故障。假设故障已知，在此基础上分别设计对应的故障补偿方案。引入故障指示函数表示没有执行器故障的情况，否则。引入故障指示函数表示执行器1故障的情况，否则。引入故障指示函数表示执行器4故障的情况，否则。综合3种故障情况，得到综合的控制律，多个控制器融合原理如图3所示。

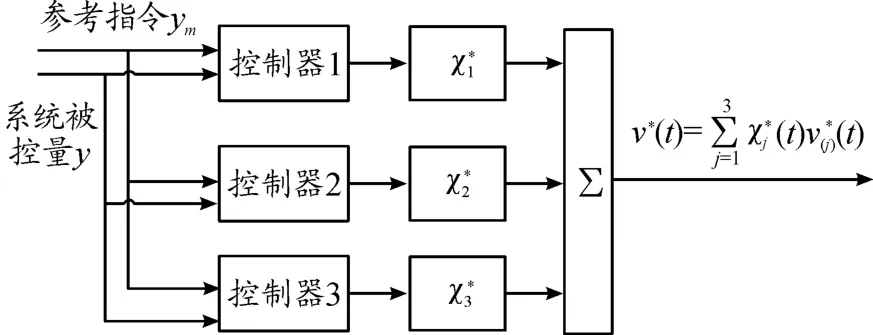
图3 多个控制器融合原理框图

1）无执行器故障时的理想故障补偿设计

设计控制信号

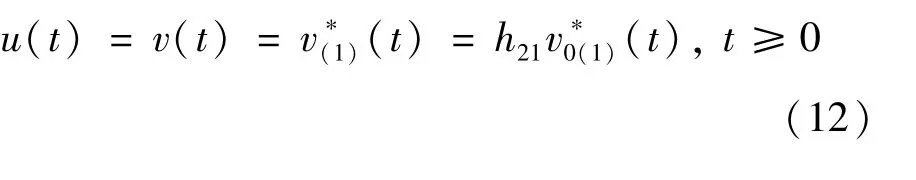
结合Backstepping控制，得到控制信号方程

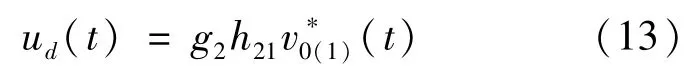
式中：h21∈R4×3的选取使g2h21为非奇异矩阵。

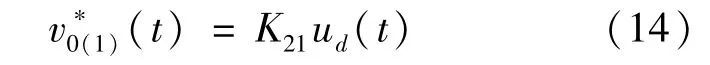
式中：K21∈R3×3，可得出。结合故障指示函数得到无执行器故障时的故障补偿器

2）执行器1故障时的故障补偿设计

设计控制信号

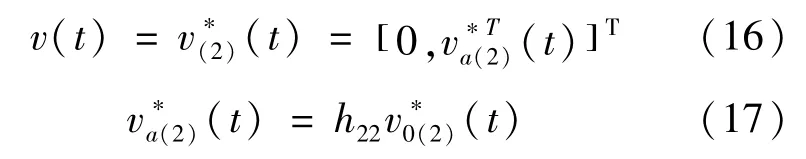
结合Backstepping控制，得到控制信号方程

式中：h22∈R3×3的选取应使g2（2）h22为非奇异矩阵。

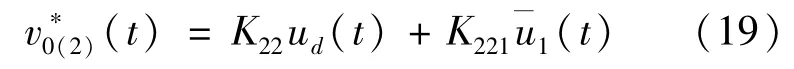
式中：K22∈R3×4，K221∈R3×3，可得出和，并解得。

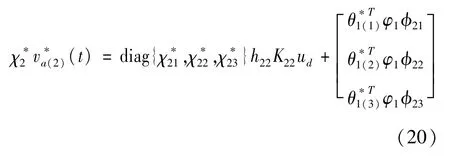
3）执行器4故障时的故障补偿设计

执行器4故障时的故障补偿设计和执行器2故障时的设计步骤类似，这里不再重复介绍，于是得到执行器4故障时的控制器为

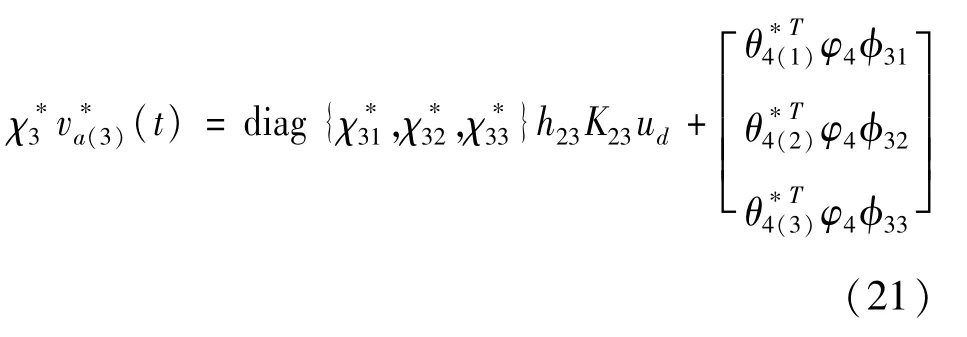
综合各故障情况，得到综合控制律为

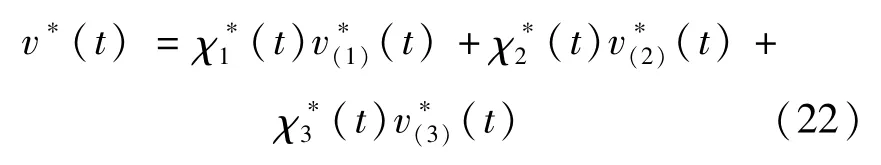
由式（15）（20）（21）可得3种故障情况下自适应补偿控制器的具体形式为

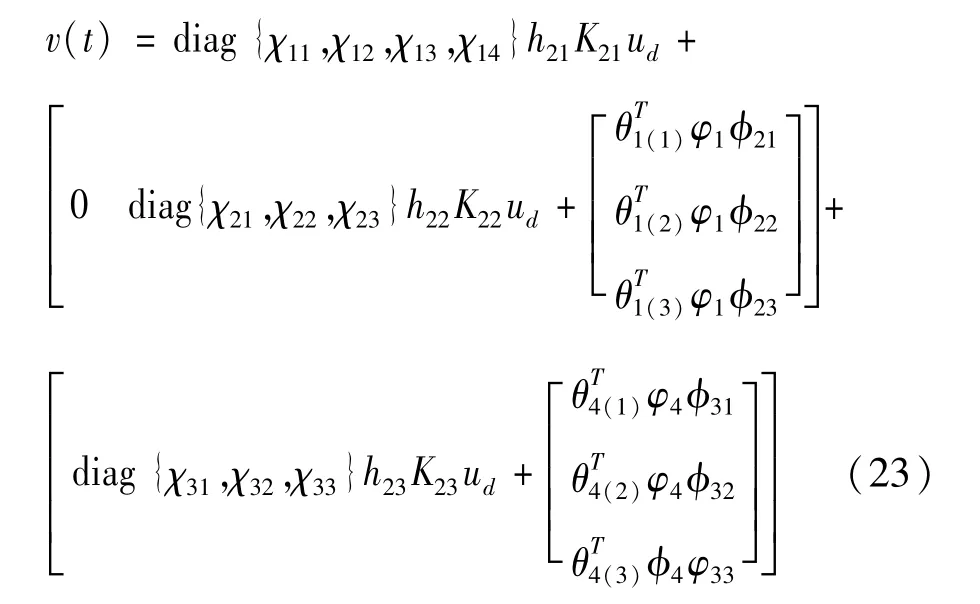
式中：χji，θ1（i），θ4（i）为 对 应 的估计值。

3.3 自适应律设计

设计控制器参数χji，θ1（i），θ4（i）的自适应律为

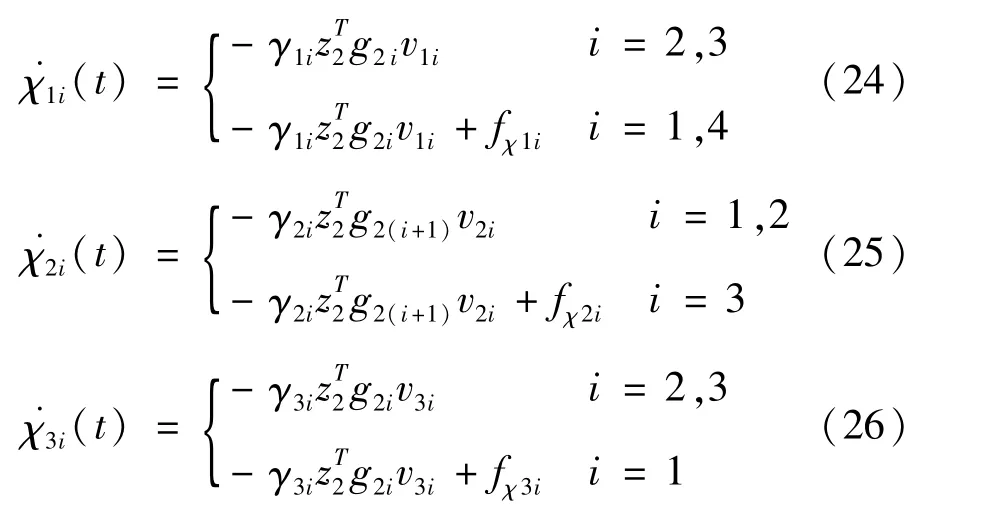
式中：γpi＞0（p=1，2，3）为自适应增益，Γ1i=为自适应增益矩阵，fχpi、fθ1（i）、fθ4（i）为投影算子［14］，保证参数有界。

3.4 容错控制器性能分析

将实际控制的控制信号u（t）和理想的控制信号ud（t）之间的误差u（t）-ud（t）转化为反馈控制信号误差v-v*，得到反馈误差信号。基于该误差信号得到各个故障模式下的Lyapunov函数。

①无执行器故障时的Lyapunov函数为

②执行器1故障时的Lyapunov函数为

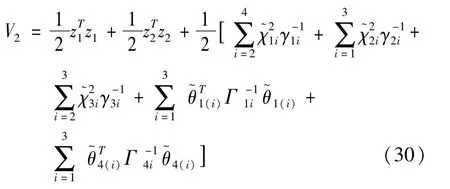
③执行器4故障时的Lyapunov函数为

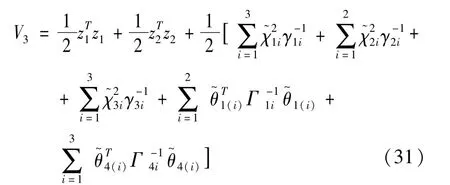
由式（8）（11）以及（24）～（28），将其代入并对上述Lyapunov函数求导，有0。由于z1=x1-ym，得从而证明

4 仿真验证及结果分析

为验证所设计的容错控制器对车辆的有效性，在Matlab编写程序后对分布式驱动电动汽车系统容错控制进行仿真与分析，利用Carsim/Simulink联合仿真，车辆模型参数详见文献［15］，具体的容错控制系统联合仿真框图如图4。

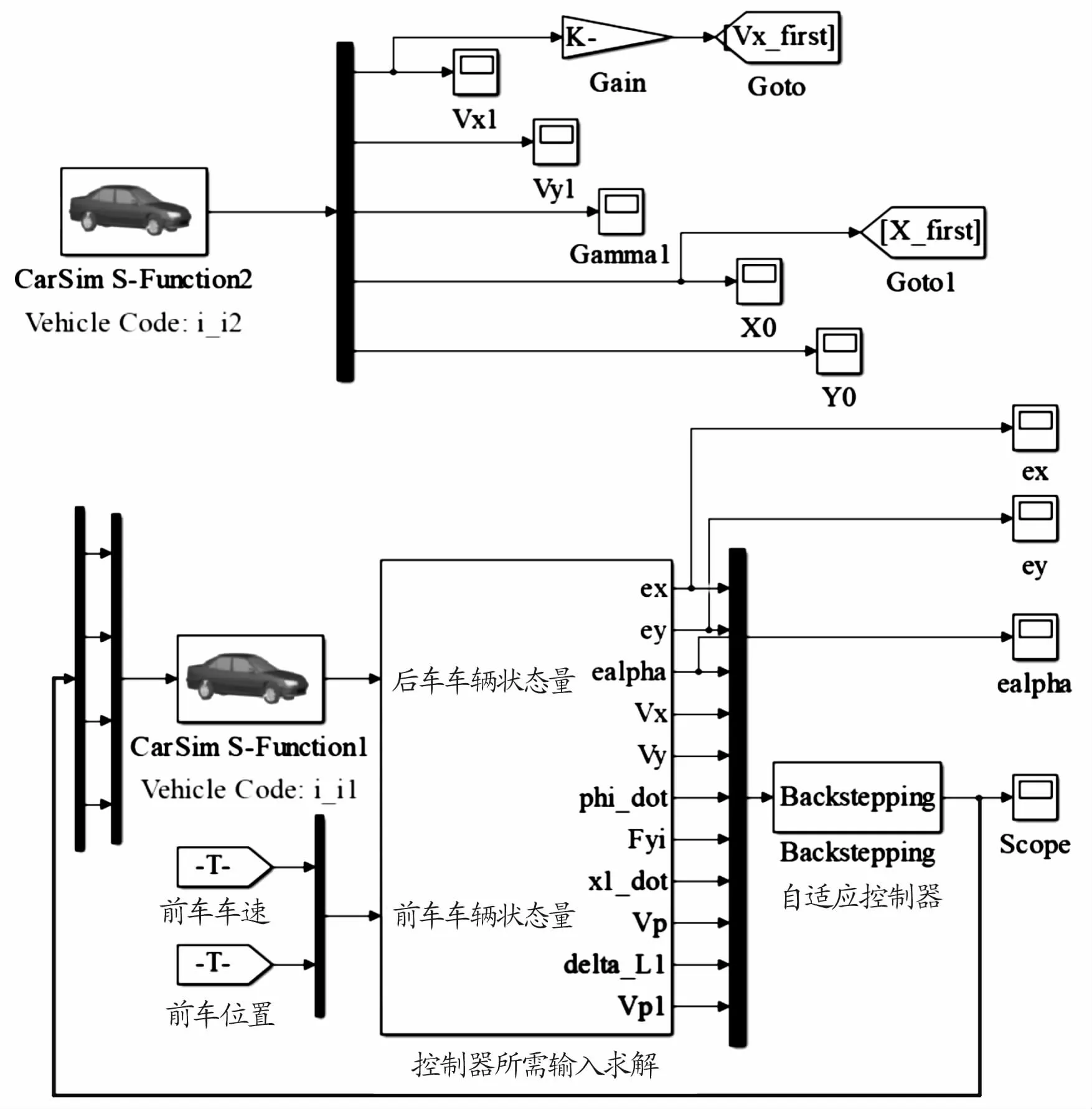
图4 容错控制系统联合仿真框图

仿真工况1：设定路面摩擦因数μ=0.8，前车速度为80 km/h，期望行车轨迹为半径30 m的圆形轨道。考虑以下情况：（i）当t＜2 s：系统无故障情况；（ii）当2 s≤t≤4 s：左前轮发生卡死故障，且故障值为5 N·m；（iii）当4 s≤t≤6 s，左前轮恢复正常；（iv）当t≥6 s：右后轮发生时变故障，且故障值为5sin（（5π/8）t）N·m。仿真中控制器参数设置为：c1=c2=15，γ1i=γ2i=γ3i=10，Γ1i=Γ4i=300，χ1i（0）=1，χ2i（0）=0，χ3i（0）=0，θ1（i）（0）=0，θ4（i）（0）=0。图5～7为工况1的仿真结果。

根据图5的仿真结果可以看出，初始偏差分别为ex=0.02 m，ey=0.5 m，eα=0.02 rad。分析图6可知，在车辆进行圆形轨迹的跟车行驶过程中，车辆在纵向、侧向及横摆3个方向依然可以保持稳定，并且能够能完成队列保持和轨迹跟踪的目标。由图7可以看出，在0～2 s无执行器故障，在2～4 s时执行器1发生卡死故障，该时间段其余的执行器重新分配驱动力矩保证车辆跟踪系统的稳定性，在4～6 s内无执行器故障，在6～10 s时执行器4发生时变故障，此时其余的执行器进行时变故障补偿。可知，当车辆发生故障时，驱动力矩相应地变化，以满足发生故障时系统的动态性能，驱动力矩会自动调整来稳定系统。

图5 输出参考指令跟踪曲线

图6 车身速度变化曲线

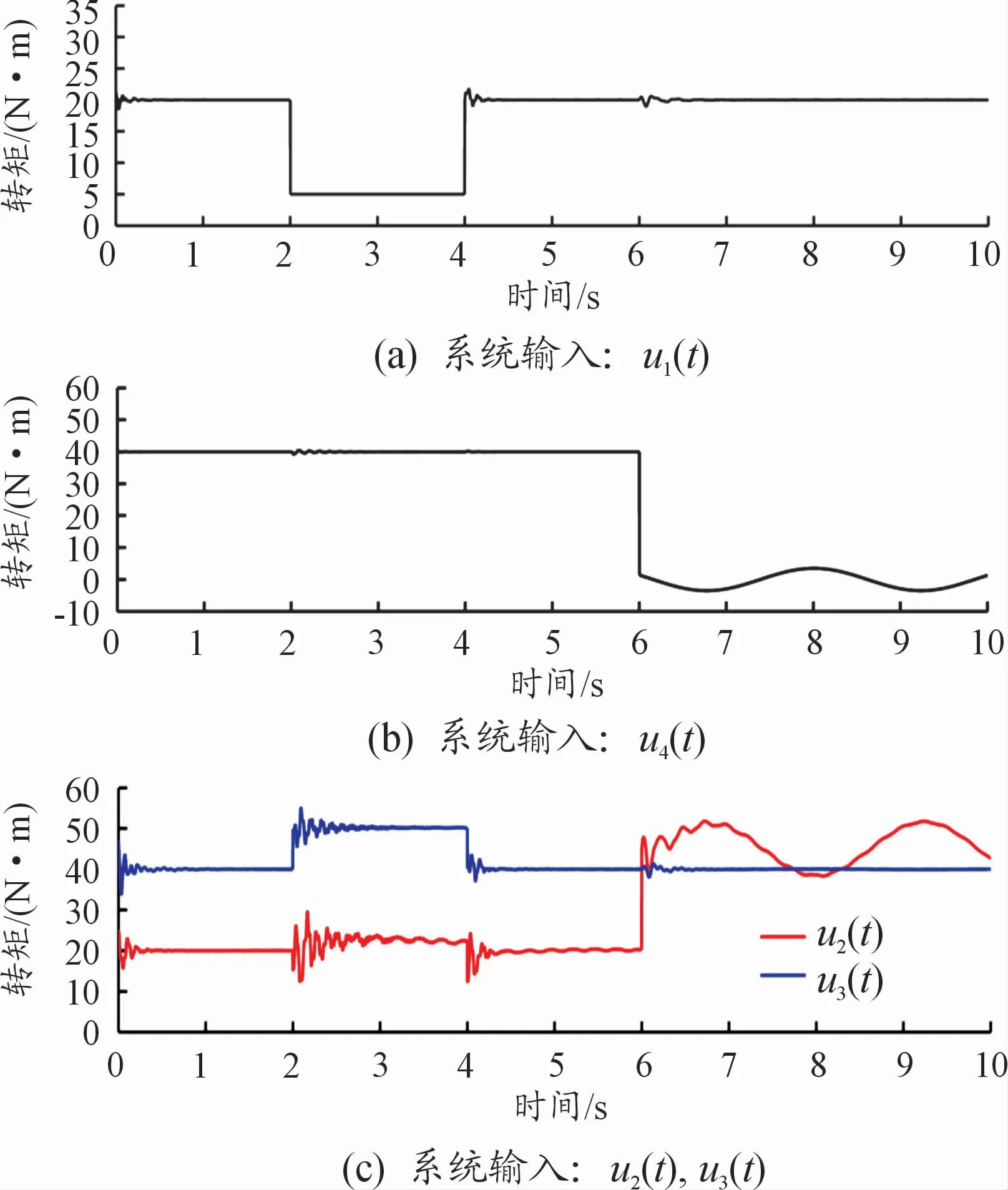
图7 控制输入信号曲线

仿真工况2：车辆在路面摩擦因数为0.8的路面行驶，前车速度为80 km/h，期望行车轨迹为半径30 m的圆形。考虑以下情况：当0 s≤t≤2 s时左前轮发生卡死故障，且故障值为5 N·m；当t≥6 s时左前轮发生部分失效故障，且失效因子为0.8，同时右后轮发生时变故障，且故障值为，其他时间段驱动电机正常工作。仿真中控制器参数设置为：c1=c2=20，Γ1i=Γ4i=350，其余控制器参数如工况1所示，图8～10为仿真工况2的仿真结果。

图8描述了驱动电动汽车的跟车及寻迹能力。从仿真结果可以看出：加入Backstepping自适应控制器的纵向位移、侧向位移及切向角度偏差随着时间的变化渐近趋近于0，车辆的稳定性较好。图9分析了车辆状态量的稳定情况，当车辆同时发生2个不确定执行器故障时，车辆在纵向、侧向、横摆3个方向依然可以保持稳定。车身速度也是Backstepping自适应控制器设计的中间量，可见设计的控制器具有较强的鲁棒性。图10中当2个执行器同时发生故障时，本文所提的故障补偿算法能够扩展用于解决多个执行器故障问题，能及时调整其他执行器抑制故障对系统性能的影响。

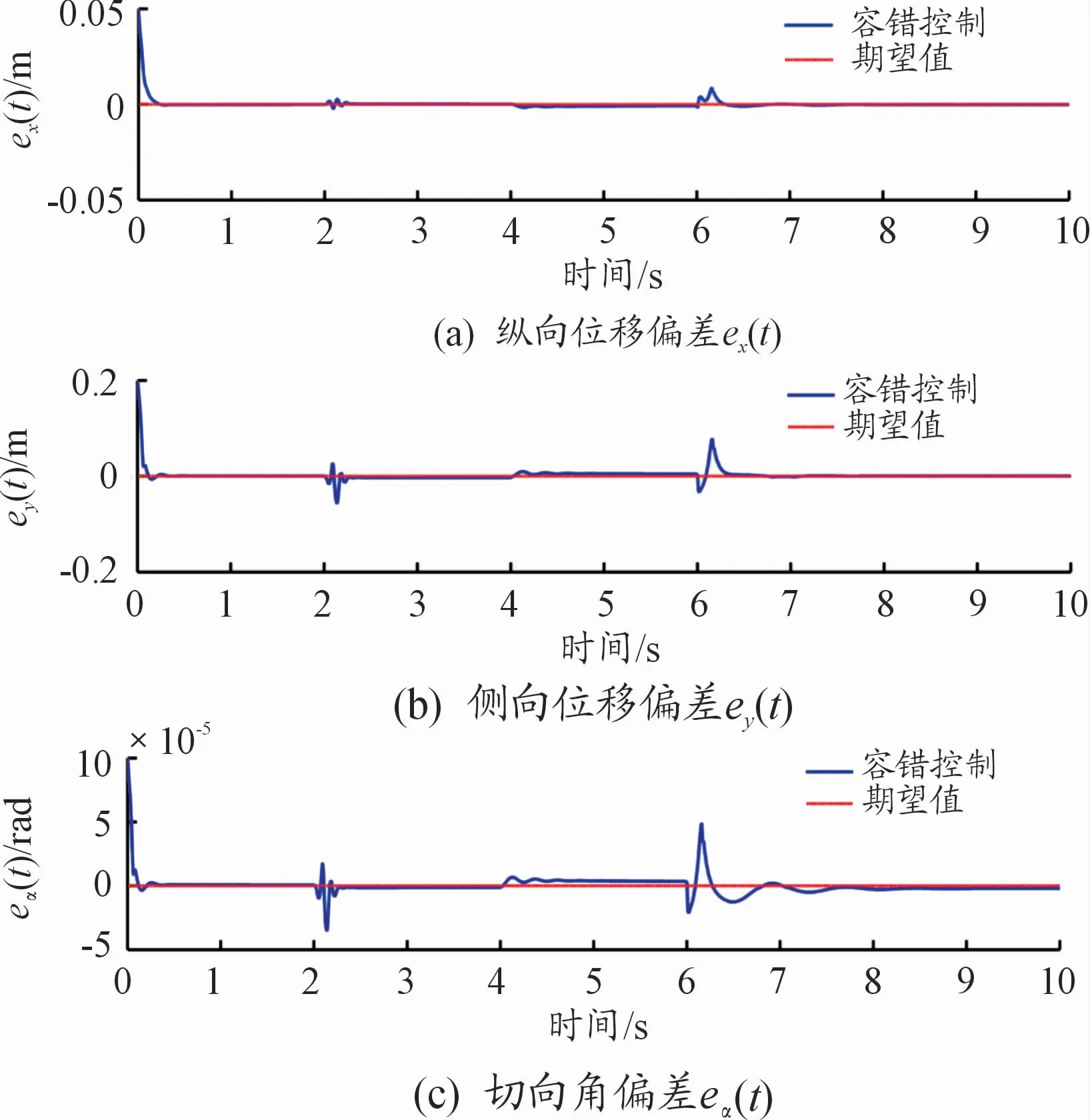
图8 输出参考指令跟踪曲线

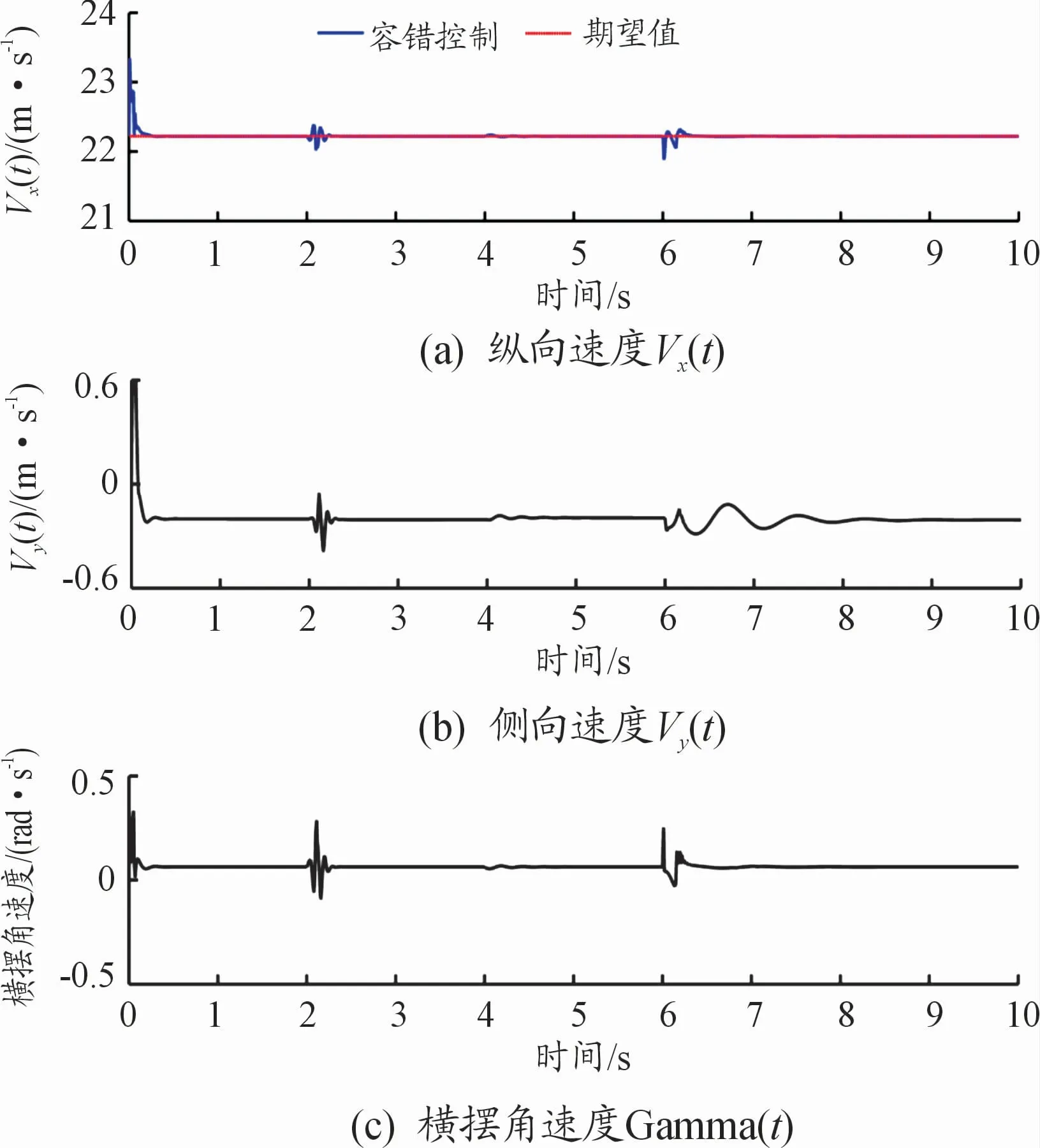
图9 车身速度变化曲线

图10 控制输入信号曲线

通过上述仿真实验结果及其分析可以看出，当分布式驱动电动汽车发生执行器故障时，所设计的Backstepping自适应容错控制器能快速地处理不确定故障给车辆系统带来的影响，故障发生后的瞬态误差也随时间减小，同时也保证了参考信号的跟踪性能。

5 结论

1）基于Backstepping自适应的驱动电动汽车容错控制方法能解决不确定执行器故障情况下车辆的输出跟踪控制问题，且解决的故障问题具有多样性，提高了车辆的操纵稳定性和行驶安全性。

2）基于Backstepping自适应的驱动电动汽车容错控制方法能够用一个综合控制器解决多重不确定执行器故障，且不需要故障检测和故障诊断单元，具有更好的经济效益。