基于模型预测控制的电动汽车起步工况仿真与性能评价

李文礼，陆 宇，汪杨凡，郑维东，严海燕，徐 瑞

（1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室，重庆 400054；2.大陆汽车研发（重庆）有限公司，重庆 404100；3.东风汽车股份有限公司 东风商品研发院，武汉 430056）

近年来，电动汽车由于具有节能、环保、能量效率高等优点，在国内发展迅速。相对于传统燃油汽车，电动汽车的电驱动系统没有离合器的辅助，如果缺乏合理的控制策略，会在启动过程中出现抖动现象，因此汽车起步工况是电动汽车电驱动系统的重要工况，其性能反映了电驱动系统及整车的控制策略优劣，对电动汽车起步过程的研究具有重要意义［1-6］。

国内外学者对汽车起步控制进行了较为深入的研究。胡建军等［4］在考虑驾驶员意图的基础上，提出纯电动汽车无油门起步和有油门起步两种模式下的起步控制策略，仿真结果表明所提出的控制策略充分反映了驾驶员意图，控制效果理想。吴兵显等［5］提出一种驱动电机和制动器相配合的自适应起步控制方法，从起步冲击度和溜坡距离两个坡道起步评价指标验证了所提出控制方法的有效性。罗石等［6］根据加速踏板开度与加速踏板开度变化率制定基于模糊推理的驾驶员意图解析策略，并基于该策略和车辆实际运行情况制定电机转矩的控制策略，从速度、电机输出转矩和冲击度3个方面验证控制策略的可行性。秦大同等［7］针对不同的驾驶员意图起步操作模式，分别制定相应的控制策略，提高了纯电动汽车起步时的动力性和操控性。近年来，很多学者把模型预测控制（model predictive control，MPC）策略应用在汽车控制领域，获得了较好的效果。辛喆等［8］利用MPC方法实现了智能汽车的轨迹跟踪，同时保证了智能汽车行驶稳定性和安全性。谢辉等［9］针对具有高度非线性、强耦合的无人驾驶汽车运动控制问题，提出一种基于MPC的横纵向综合控制方法，实现了车辆的速度跟踪。李绍松等［10］提出一种改进型线性时变MPC方法，提高了极限工况下主动前轮转向汽车的稳定性。唐小林等［11］在多车速度规划与跟驰模型基础上设计了MPC算法来规划汽车队列的未来车速，以达到提高混合动力汽车车队的跟车稳定性的目的。

MPC方法可以很好地处理各种带约束的线性、非线性问题。为提高电动汽车起步工况下的性能，采用MPC方法对电动汽车起步过程进行控制。首先建立纯电动汽车整车模型和驾驶员模型，基于MPC方法建立的驾驶员模型利用上层控制器得到期望加速度，下层控制器根据期望加速度得到加速指令和减速指令，从而对车辆进行起步工况的加、减速控制。给出起步时间、驱动电机电压电流和冲击度3个评价指标，分别进行不同坡度（0%，10%和20%）下电动汽车起步工况的仿真试验，并根据评价指标对试验结果进行分析。

1 纯电动汽车整车模型

为了进行电动汽车起步工况的仿真试验，需要建立纯电动汽车整车模型，主要包括整车控制器模型、驱动电机模型、传动系和轮胎模型［12］。

1.1 整车控制器模型

整车控制器是纯电动汽车的核心控制部件，本文中根据仿真需求对整车控制器模型进行简化，主要结构包括如图1所示的根据踏板开度计算电机转矩需求模块。

图1 电机转矩需求计算模块示意图

1.2 驱动电机模型

选取永磁同步电机作为电动汽车驱动单元进行建模，其数学模型主要包括电压平衡方程、磁链方程和转矩方程。一般对驱动电机数学模型进行简化分析，做以下假设［13］：

1）定子绕组为Y型连接，三相绕组对称分布，各个绕组的轴线在空间互差120°；

2）不计转子阻尼；

3）忽略电机中的涡流和磁滞损耗。

4）忽略绕组电阻与电感的变化；

1.2.1 电压平衡方程

根据永磁同步电机原理，定子电压平衡方程表示为：

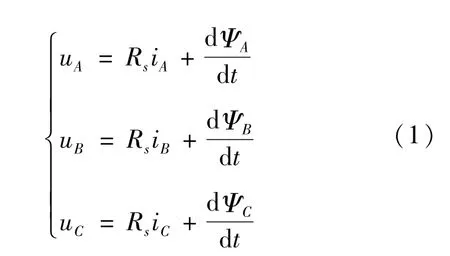
式中：uA、uB、uC为三项绕组各相的电压；Rs为三相绕组电阻；iA、iB、iC为三项绕组各相的电流；ΨA、ΨB、ΨC为三项绕组各匝链磁链。

1.2.2 磁链方程

磁链又称为磁通匝，其方程表达式为：

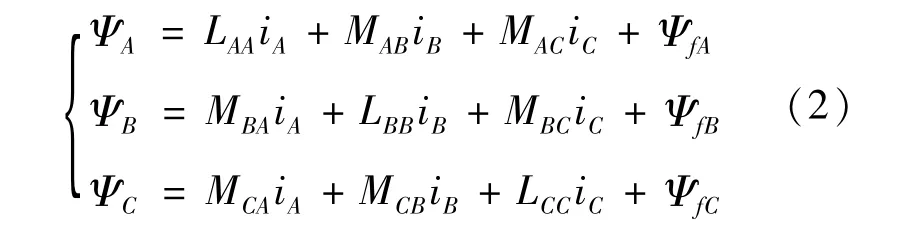
式中：LAA、LBB、LCC为三相定子绕组自感；MAB=MBA、MBC=MCB、MCA=MAC为每项绕组互感；ΨfA、ΨfB、ΨfC为转子励磁磁场匝链至定子绕组的磁链。

1.2.3 转矩方程

假设电机运行时电流一定，电磁转矩可以表示为磁场储能对机械角度θm的偏导，则电磁转矩Te表示为：

式中：np为极对数；［L］为电机自感和互感矩阵；［Ψ（θe）］为电机永磁转子磁链矩阵；θe为电气角度。

1.3 传动系统和轮胎模型

传动系采用前驱单速比机械式变速器，驱动电机输出动力给变速器，经差速器后传递给车轮，因此，建立的纯电动汽车传动系统模型如图2所示。

图2 纯电动汽车动力传动系统模型示意图

纯电动汽车起步过程仿真中，为了更加准确地反映实际道路情况，对轮胎模型精度有较高要求，这里选取魔术公式的轮胎模型进行建模。魔术公式的原理［14］是利用三角函数组合的形式来拟合轮胎的试验数据，进而得到一套形式相同的公式来表达轮胎的侧向力、纵向力、回正力矩、翻转力矩、阻力矩以及侧向力、纵向力联合作用等工况。魔术公式的一般表达形式为［15］：

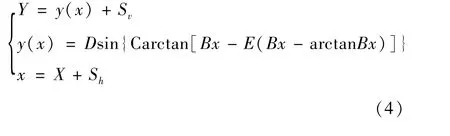
式中：Y为侧向力、纵向力或回正力矩；X为侧偏角或纵向滑移率；D为峰值因子；B为刚度因子；C为曲线形状因子；E为曲线曲率因子；Sh、Sv分别为曲线水平方向及垂直方向的漂移。

图3为建立的轮胎动力学模型示意图。

图3 轮胎动力学模型示意图

2 驾驶员模型

2.1 驾驶员意图解析

车辆在行驶过程中，驾驶员通过将其主观意愿和周围实时道路情况相结合对车辆进行加速、减速和转弯等操作。为了简化驾驶员意图，可将其转化为加速踏板开度变化和制动踏板开度变化，即当驾驶员期望加速时加大加速踏板、松开制动踏板，当驾驶员期望减速时松开加速踏板、加大制动踏板。

2.2 基于MPC的驾驶员模型设计

图4为基于MPC的驾驶员模型结构。其中上层控制器基于MPC方法得到期望加速度，下层控制器根据期望加速度得到加速指令和减速指令，从而对车辆进行自动加、减速控制［9，16-18］。

图4 基于MPC的驾驶员模型结构框图

2.2.1 层控制器设计

车辆的期望加速度ades与实际加速度a之间的关系可由1阶惯性环节来近似表示［17］：

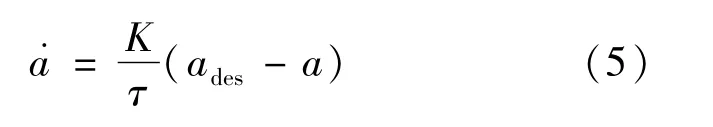
式中：K为系统增益；τ为时间常数。其连续系统的状态空间方程可表示为：

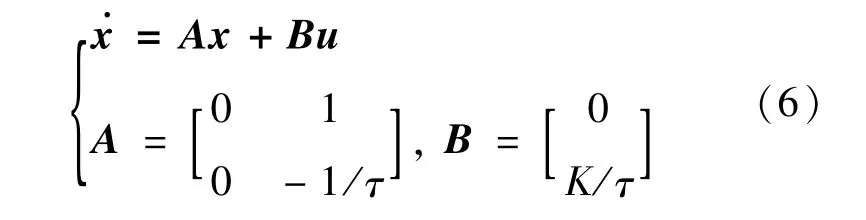
式中：x=［v a］T为系统状态变量；u=ades为系统控制输入。

对式（6）进行离散化处理，得到离散系统的状态空间方程为：

式中：k为当前采样时刻，k+1为下一个采样时刻；T为采样周期。

控制系统的输出变量为速度，则输出方程可以表示为：

式中，Ck=［1 0］。

考虑到系统控制目标为在不产生较大加速度及加速度变化率的前提下实现纵向速度的精确跟踪，设计优化目标函数为：

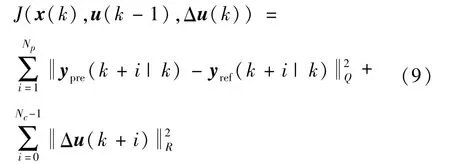
式中：k-1为上一个采样时刻；Np为预测时域，Nc为控制时域；ypre（k+i|k）为系统输出变量的预测值，yref（k+i|k）为系统输出变量的参考值，（k+i|k）表示以k时刻的系统输出量来预测k+i时刻的值，其中i=1，2，…，Np；Δu（k）和Δu（k+i）分别为k时刻和k+i时刻系统控制输入增量，即加速度增量，其中i=0，1，…，Nc-1；Q和R为权重矩阵。

系统需要对控制输入的加速度及其增量施加约束条件，即：

式中：umin和umax分别为加速度的阈值；Δumin和Δumax分别为加速度增量的阈值。

系统优化求解问题即在预测时域里，式（9）在满足式（10）的约束条件下达到最小。通过将上述问题转化为Matlab易于求解的二次规划问题，得到控制时域内的系统控制输入增量为：

将控制输入增量的第1项Δu（k）取出，即可得到当前时刻系统控制输入为：

2.2.2 下层控制器设计

下层控制器由驱动、制动切换逻辑和比例控制模块组成［17］。切换逻辑为将从上层控制器获得的期望加速度ades与0相比较。当ades≥0时施加驱动控制（驱动模式），当ades＜0时施加制动控制（制动模式）。由于用于仿真研究的电动汽车整车模型的输入量为yacc（即加速踏板开度）和ydec（即制动踏板开度），所以可通过简单的比例控制计算驱动、制动控制输入量。

驱动模式时，由上层控制器得到ades，则制动控制输入为ydec=0，加速踏板开度αdes=Kt×ades，Kt为加速踏板开度转换比例，则驱动控制输入为：

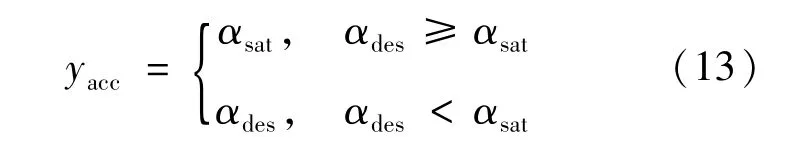
式中，αsat为加速踏板开度阈值。

制动模式时由上层控制器得到ades，则驱动控制输入为yacc=0，制动踏板开度βdes=Kb×ades，Kb为制动踏板开度转换比例，则制动控制输入为：

式中，βsat为制动踏板开度阈值。

如图5所示，上层控制器基于S函数建立了基于MPC的驾驶员模型。

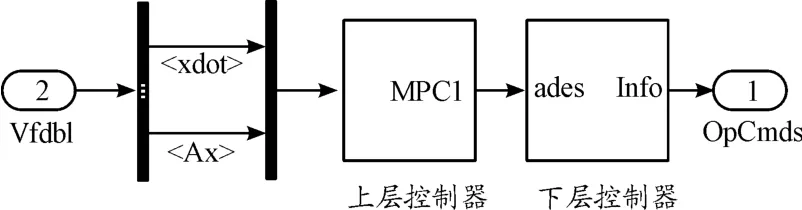
图5 基于模型预测控制的驾驶员模型框图

3 纯电动汽车起步性能评价指标

为了验证提出的基于MPC方法的驾驶员模型在纯电动汽车起步工况仿真中控制性能的有效性，从起步时间（动力性）、驱动电机电压和电流（经济性）、冲击度（舒适性）3个方面对纯电动汽车起步性能进行评价。

3.1 起步时间

由GB/T 28382—2012所要求的动力性能可知，车辆最大爬坡度不低于20%。按规定的试验方法对纯电动汽车0～80 km/h的起步加速性能进行测试时，起步加速时间不超过25 s。

3.2 驱动电机电压和电流

纯电动汽车起步过程中，驱动电机电压和电流会出现较大波动。当驱动电机电压过低时，起动转矩不足会导致电机启动困难；当驱动电机电流过高时，定子线圈会因过流而发生断路等故障。因此，车辆起步过程中，驱动电机电压和电流不易过高，以免影响其寿命。

3.3 冲击度

冲击度是评价纯电动汽车起步品质的一项重要指标，根据国家对车辆起步时冲击度的要求，设定推荐值在10 m·s-3以内。根据汽车行驶方程：

式中：ig为变速器传动比；i0为主减速器传动比；η为传动效率；r为车轮半径；G为整车重力；f为滚动阻力系数；θ为道路坡度角；CD为空气阻力系数；A为迎风面积；v为当前车速；δ为车辆旋转质量换算系数；m为车辆质量；d v/d t为车辆当前加速度。

由式（15）可得：

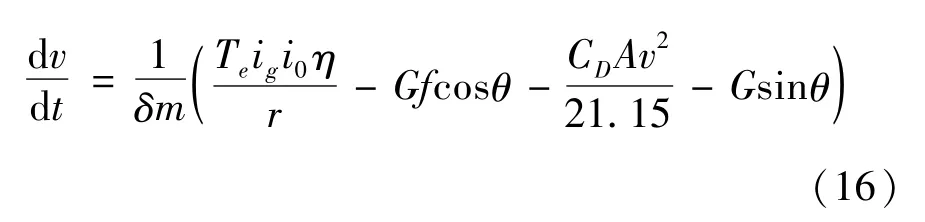
假设坡度阻力和滚动阻力的数值保持不变，忽略风阻，对式（16）求导可得冲击度j为：

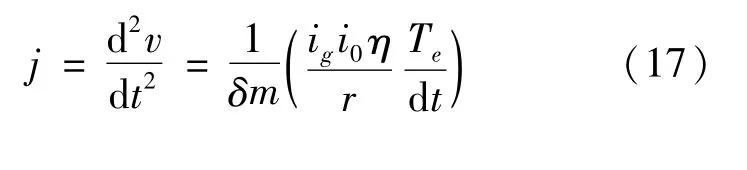
4 仿真及结果分析

在Matlab/Simulink中建立如图6所示的纯电动汽车整车模型用于仿真研究，部分仿真整车参数如表1所示。

图6 纯电动汽车整车模型框图

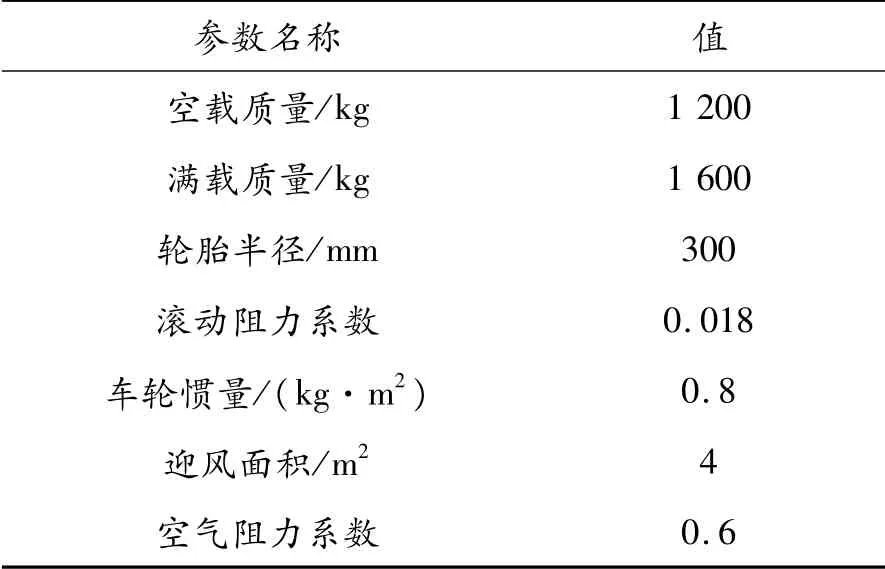
表1 整车参数

为了较好地研究纯电动汽车起步过程的各项性能指标，对提出的基于MPC方法的驾驶员模型进行不同坡度下起步过程的仿真，并与常规PID控制的驾驶员模型的控制性能进行比较。仿真参数及试验工况设置为：

1）Simulink仿真环境：参考GB/T 28382—2012的动力性能要求以及乘车舒适度，为较好反映纯电动汽车起步工况，仿真时长设为20 s，第10 s的期望车速设为15 km/h，设定采样时间为0.001 s；

2）PID控制器参数：比例系数设为1.5，积分系数设为1.5，微分系数设为0；MPC控制器参数：预测时域设为30，控制时域设为15，权重取值Q=100，R=1；

3）试验工况：设置在3种路面上进行起步工况仿真试验，即路面的坡度分别设为0%、10%及20%。

根据设置的仿真参数及试验工况进行仿真试验，得到的仿真结果如图7～12所示，其中图7～10均为车辆空载时在不同坡度下起步的仿真结果。由图7、8可知，分别使用MPC和PID控制方法的驾驶员模型进行仿真时，在起步初期，坡度越大，电压电流变化越大，但电机电压、电流均在正常变化范围内。在达到目标车速后，电机电压、电流有所波动，PID控制方法下的曲线的超调量大于MPC方法。由图9、10可知，2种控制方法起步响应时间均为11 s左右，起步响应达到预期控制效果，使用MPC方法的驾驶员模型时起步响应更快，其超调量也小于PID控制方法。

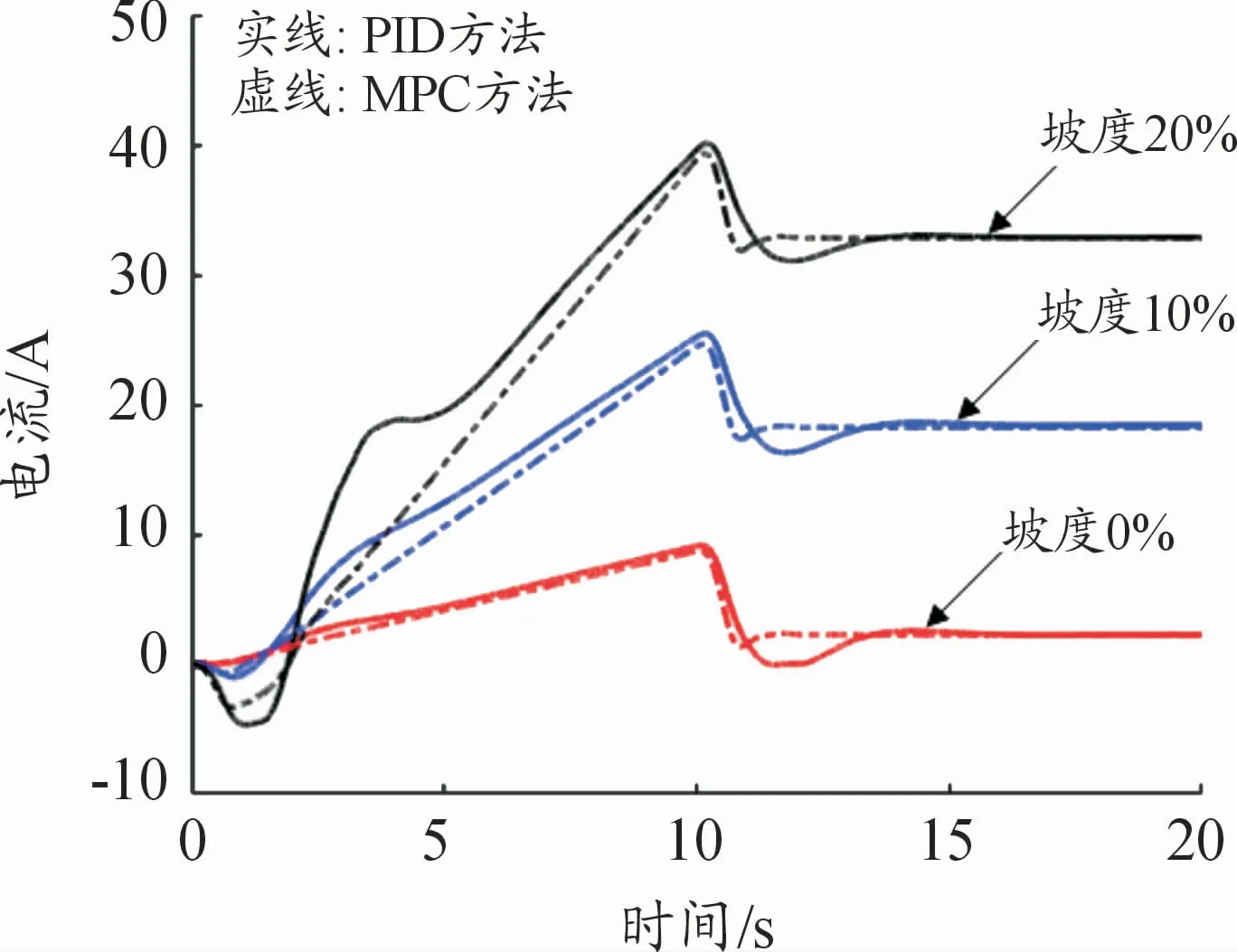
图7 不同坡度下起步驱动电机电流仿真结果

图8 不同坡度下起步驱动电机电压仿真结果

图9 不同坡度下起步驱动电机扭矩仿真结果

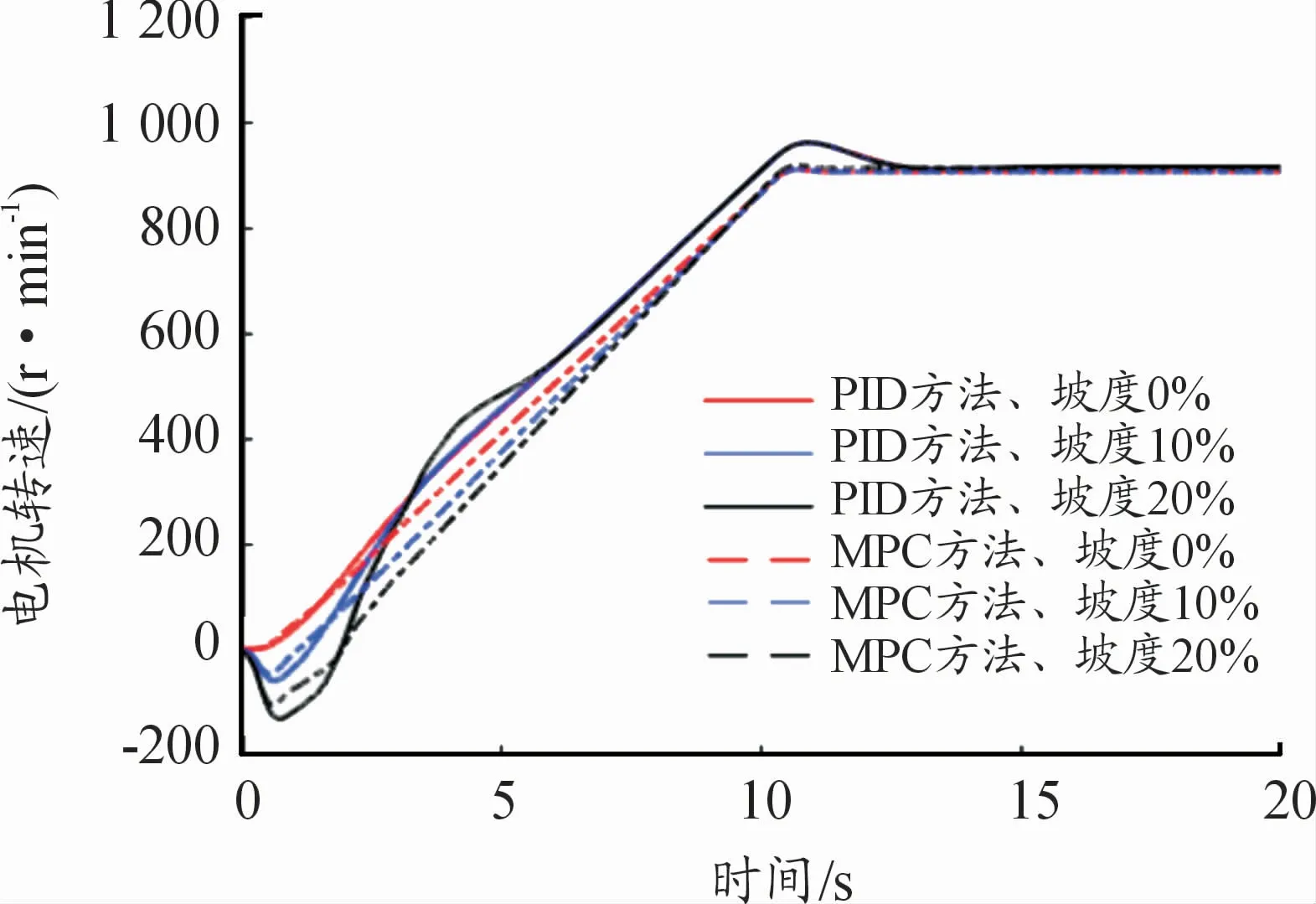
图10 不同坡度下起步驱动电机转速仿真结果

考虑车辆负载对起步性能的影响，图11～12为加入不同负载（空载、半载和满载）的车辆在10%坡度下起步时的仿真结果。由图11、12可知：在设定的驾驶员期望车速及起步时间一致的情况下，加速踏板开度仿真结果可以较真实地反映驾驶员在不同坡度下起步时的操控过程，加速踏板开度随着车辆负载增加而增大。起步初期0～6 s内，冲击度较大，且最大值出现在20%的坡度下起步时，MPC方法下的驾驶员模型的瞬时最大值约为3.9 m·s-3，PID控制方法下的驾驶员模型的瞬时最大值约为4.1 m·s-3，均低于国家对车辆起步时冲击度设定的推荐值10 m·s-3；随着车辆负载的增加，2种控制方法下的最大冲击度都会相应增加，在10%坡度下起步时均低于3 m·s-3；在6～9 s内，车辆处于短暂的匀加速行驶阶段，冲击度变化较小；在9～13 s内，车辆达到设定的驾驶员期望车速15 km/h，为了保持该车速，驱动电机的扭矩需求变小，从而使得冲击度较大；在13 s后车辆匀速行驶，冲击度较小。

图11 不同坡度下起步加速踏板开度仿真结果

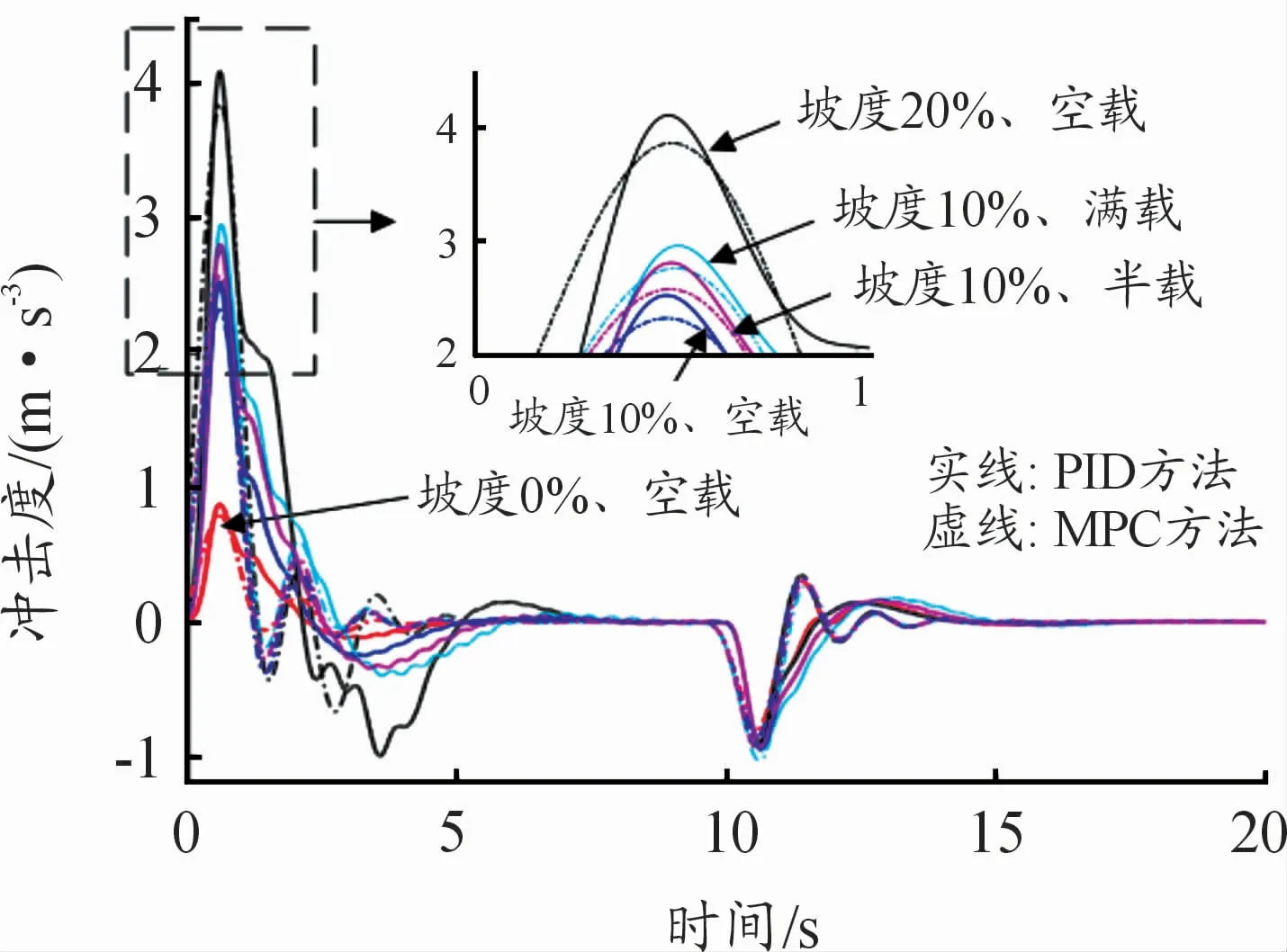
图12 不同坡度下起步冲击度仿真结果

5 结论

提出一种基于MPC的驾驶员模型，用于电动汽车起步工况仿真的控制性能研究。建立了较为完整的纯电动汽车整车模型和驾驶员模型，其中驾驶员模型包括上层控制器和下层控制器。上层控制器基于MPC方法求出期望加速度，下层控制器则由期望加速度来判断驱动、制动切换逻辑，求出纯电动汽车整车模型在进行起步工况仿真时需要的加、减速指令，进而得到电机需求转矩。

给出了起步时间、驱动电机电压电流和冲击度3个纯电动汽车起步性能评价指标，分别在不同坡度（0%，10%和20%）下进行起步工况的仿真试验。利用试验结果在给出的起步性能评价指标下分析了基于MPC的驾驶员模型的控制性能，并与常规基于PID控制的驾驶员模型的控制性能进行了比较。仿真结果验证了基于MPC的驾驶员模型在起步工况仿真中控制性能的有效性，所提出的仿真方法可为电动汽车电驱动系统性能研究提供参考。