熵热系数取值方式对锂离子电池热模型精度的影响

栗欢欢，竺玉强，王效宇，裴 磊

（江苏大学 汽车工程研究院，江苏 镇江 212013）

近些年来，环境污染与能源短缺已成为亟待解决的难题，引起全世界范围内的广泛重关注。新能源汽车凭借其节能、环保等优势已从概念车走向产业化发展。动力电池作为新能源汽车的主要动力来源及核心部件［1］，对其准确建模及有效控制直接影响到汽车的动力性和安全性。

目前，锂离子电池的最佳工作温度为25℃到40℃，过高或过低的温度都会对其容量、循环寿命、最大功率等性能特性产生较大影响，严重时甚至会导致电池热失控，引起火灾，严重威胁到乘用人员的生命财产安全［2-3］。因此，建立能准确预测电池温度变化的热模型，对于电池热管理系统的设计与车辆的整体安全性具有重要意义［4-6］。

在这一研究领域，早在20世纪80年代，Bernadia等学者就对电化学-热耦合模型进行研究，提出了一种电池生热速率的经典模型并被广泛应用至今［7］。在此基础上，随着相关研究的不断完善，更多多维热模型也逐渐发展起来［8-10］。目前，在电池生热速率模型的建立过程中，由于其内阻、熵热系数等参数在电池充放电过程中会持续发生变化且难以实时直接测量，所以其取值一般通过各种假设进行相应简化。其中，文献［5］将所涉及内阻、熵热系数等参数均以固定值方式处理，建模时给电池以恒定生热速率，忽略电池放电过程中的生热变化情况［5］。文献［6］则是研究了内阻简化方式对热模型精度的影响，表明动态内阻取值能够获取更好的热模型精度。但是，现有文献主要关注内阻变化对电池生热速率的影响，对熵热系数的影响关注较少。熵热为电池放电过程中产生可逆热，熵热数值在放电过程中不断变化。文献［7］通过研究发现，电压和熵热系数同样是影响电池温升变化的关键因素。由于电池高倍率放电时以不可逆阻抗热为主，所以一般情况下将熵热系数取定值简化计算。但对于三元电池这类熵热系数变化较为剧烈的电池体系，这种简化将会对电池温升计算产生较大的影响。

为了研究熵热系数取值方式对电池热模型精度的具体影响，本文选择三元电池熵热系数作为研究对象，基于三维热模型，分别采用定熵热系数和动态熵热系数模型对春兰30Ah三元方形铝壳锂离子电池进行热特性仿真研究，并将仿真结果与实际实验结果进行对比，分析说明这两种取值方式对模型精度的影响情况。

1 热模型仿真

1.1 数学模型构建

由于电池内部组成部分较多，生热情况复杂，在建立热模型时首先需要对电池内部材料的物理属性做出一些假设，具体如下［8］：

1）电池工作时内部各区域电流密度分布均匀；

2）电池内部各层材料分布均匀，热物性参数（即比热容、导热系数和密度）各向同性；

3）电池内部各层材料的热物性参数不随温度与荷电状态（SOC）变化；

4）电池内部传热主要方式为热传导，忽略热辐射与电解液的对流换热作用；

基于上述假设，以电池内核任意一微元体作为研究对象。根据热力学定律可知，微元体在任意时刻都处于能量守恒状态。微元体作为生热源［9］，其热量一部分用作自身能量的增加，一部分用来与周围物体进行能量交换［10］。结合傅里叶定律，经推导可得到电池内核的导热微分方程：

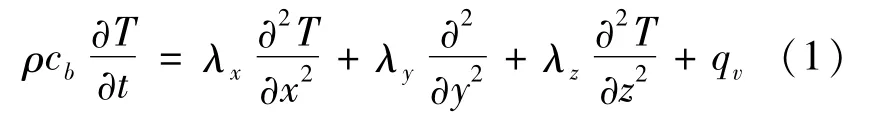
式中：ρ为电池内核密度（kg/m3）；cb为电池内核比热容（J/（kg·K））；T为微元体温度（℃）；λx、λy、λz为电池内核沿坐标轴方向的导热系数（W/（m·K））；qv为内核单位体积生热速率（W/m3）。根据Bernadia生热速率模型，得到qv的表达式为：

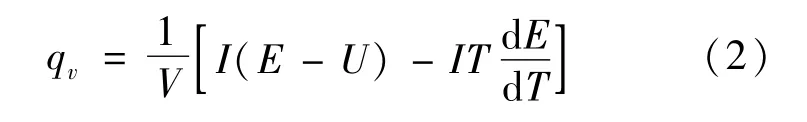
式中：I为放电电流（A）；V为电池内核体积（m3）；E为开路电压（V）；U为端电压（V）。

I（E-U）为电池放电过程中内阻产热的不可逆热，电池内阻包括欧姆内阻Ro和极化内阻Rp，两者之和统称为等效内阻Re，单位为Ω，即Re=Ro+Rp，可以通过内阻测试实验获得电池放电过程中的等效内阻值，所以上式可变为：

考虑到式（1）在不加限制的条件下有无穷多个解，为了保证解的唯一性，需要根据实际问题添加相应的初始条件，包括初始边界对流换热条件和温度条件，具体如下：

初始温度分布：

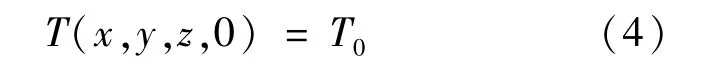
式中：T0为电池放电初始时刻温度。

边界条件由牛顿冷却定律可知：

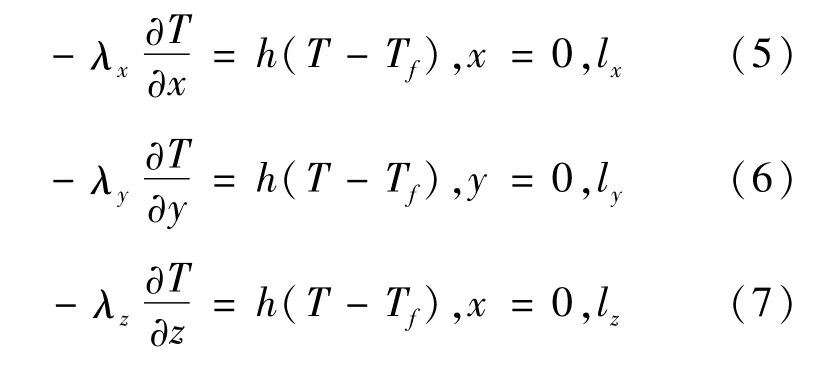
式中：h为电池表面对流换热系数；Tf为环境温度（℃）；lx、ly、lz分别为电池在x、y、z轴上的总长度（m）。本文中z轴沿方形电池厚度方向。

基于式（1）～（7），将采用有限元分析方式，对电池进行热仿真分析。

1.2 熵热系数获取

熵热代表电池内部化学反应所产生的可逆热，简化后的Bernadia生热速率公式中，IT d E/d T即为熵热的表达式。通过测量不同温度和不同SOC下电池的开路电压值，经计算可得熵热系数值。

1.2.1 变熵热系数

电池正负极材料决定了电池熵热系数数值，且该数值随电池SOC的不同而有所改变。根据本文使用的电池，选取5℃、15℃、25℃作为环境温度，具体测量步骤如下：

1）在室温条件下，对电池以（1 C）恒流恒压充满电，截止电压为4.2 V，截止电流为0.05 C，静置10 h。

2）每隔3 h改变一次恒温箱温度，依次调为15℃、25℃，分别记录开路电压值。

3）在室温条件下，将电池每放电额定容量10%，静置20 h，重复步骤2）和步骤3）。

4）重复步骤2）～4），计算得出电池在不同SOC下的的熵热系数值。

根据表1中测得的熵热系数值，拟合熵热系数随SOC变化的曲线。

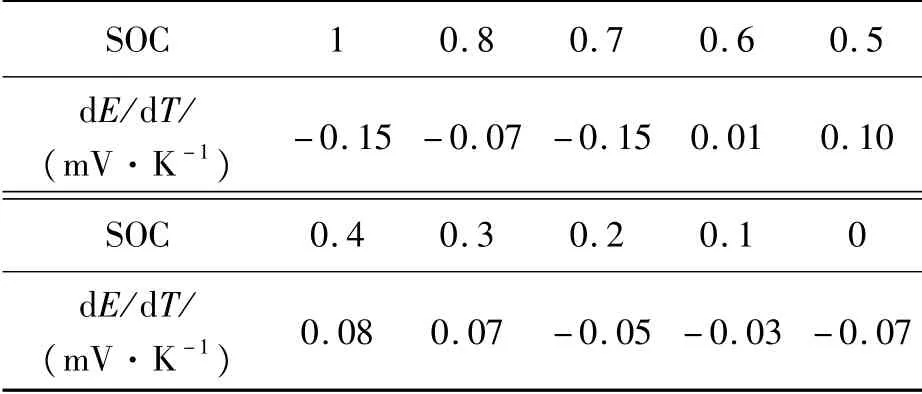
表1 不同SOC下的熵热系数值

如图1所示，由于熵热系数实验曲线存在一定程度的非平滑性，若采用常规的多项式拟合，曲线不能很好的和实际数值匹配，所以本文采用分段函数方式表征熵热系数随SOC变化的规律，并取得了良好的拟合效果，其具体函数关系式如下：

0.5 ＜SOC≤1时：

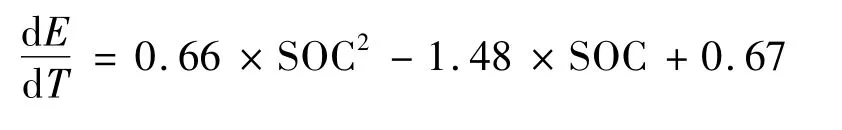
0.2 ＜SOC≤0.5时：

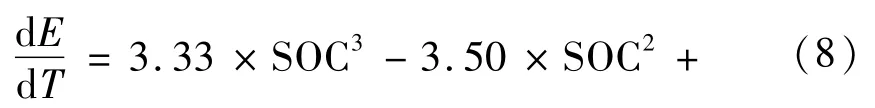
1.32 ×SOC-0.10

0≤SOC≤0.2时：

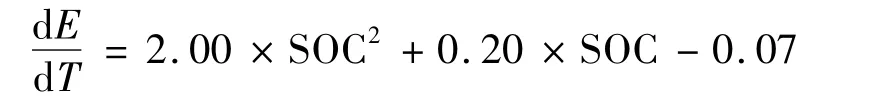
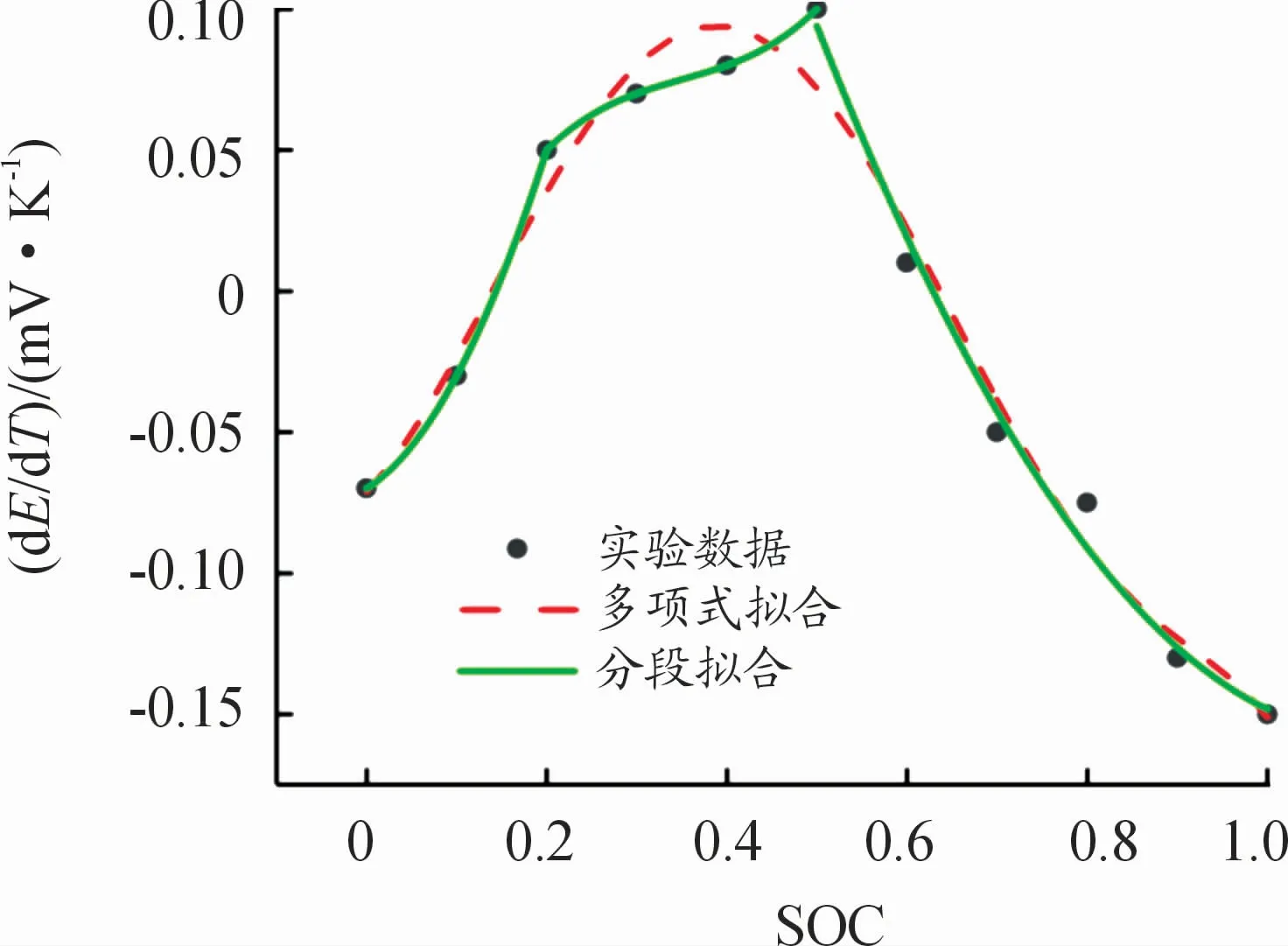
图1 熵热系数拟合曲线

1.2.2 定熵热系数

为了对比研究不同熵热系数取值对生热仿真情况的影响，本文还将测试的得到的不同SOC下的熵热系数取平均值，用以分析传统取值对热模型精度的影响情况，具体计算公式如下：

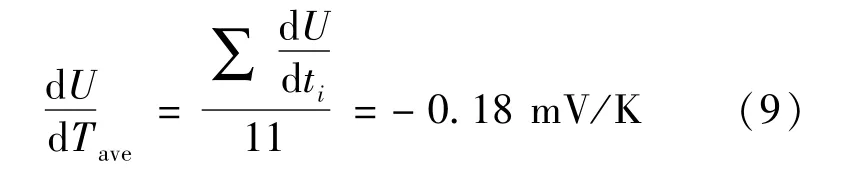
1.3 热仿真所需其他参数获取

三维热模型中除了熵热系数外，还有部分其他参数如内阻等需要通过相应方法获取。

1.3.1 热物性参数获取

式（1）中电池内核密度、比热容和导热系数难以通过实验直接获得，目前比较常用的获取方法是对电池各组分热物性参数进行加权计算。方形锂电池的内核部分由各层材料有序堆叠而成，而这种层叠结构直接导致了电池导热系数的各向异性［11］。表2为电池各组分热物性参数数据。

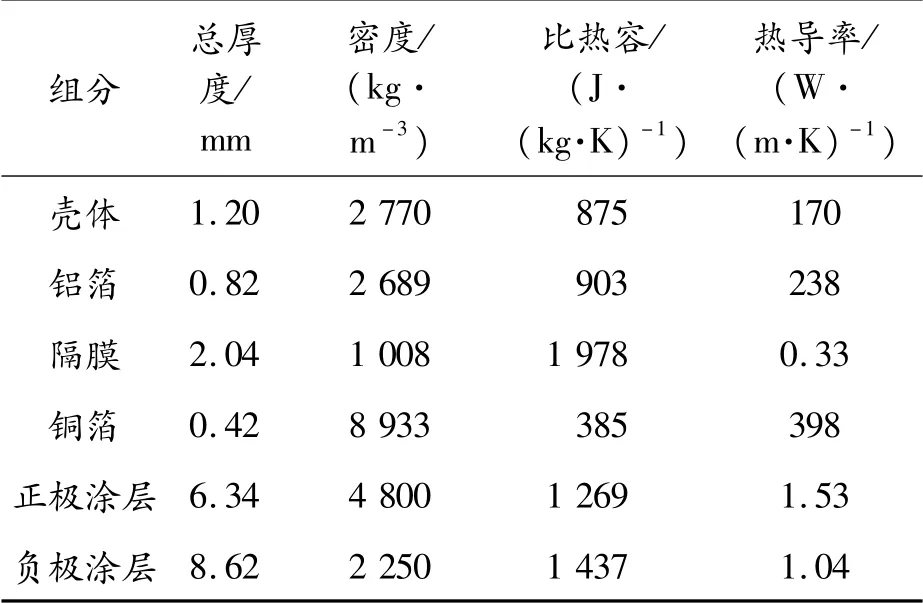
表2 电池各组分热物性参数

具体加权公式如下［12］：

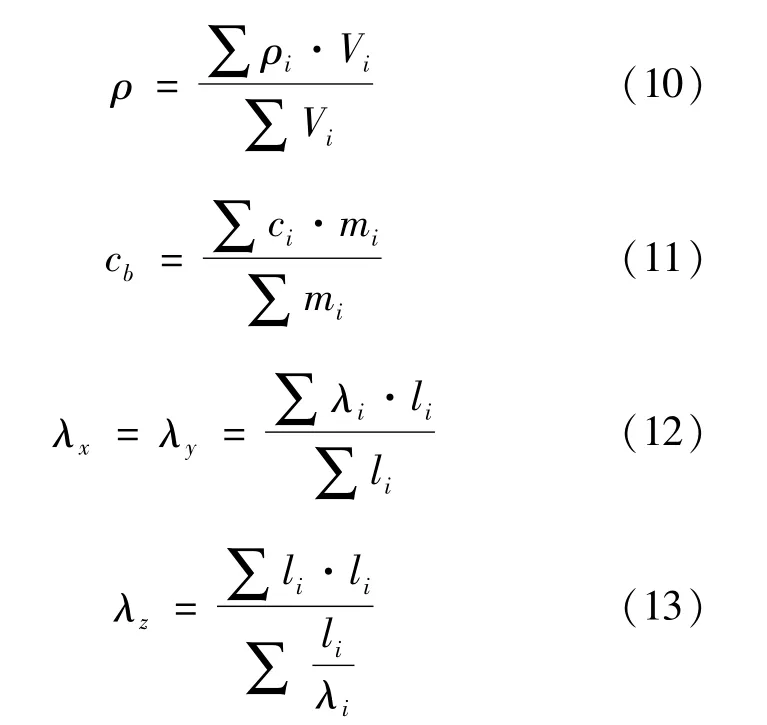
式中：ρi、ci、λi分别为电池内核各组分的密度、比热容、热导率；Vi、mi、li分别为电池内核各组分在内核区域中的总体积、总质量和总厚度。计算结果如表3所示。

表3 电池内核热物性参数

1.3.2 等效内阻获取

放电倍率、放电深度等因素都会对电池内阻产生影响［13］，本文将电流和荷电状态（SOC）作为主要影响因素，通过多项式拟合，得到内阻随电流、SOC变化的关系式。

电池内阻测试方法很多，目前研究领域中用的比较多的是混合脉冲功率特性测试方法（HPPC）［14］。结合使用的电池，具体测试步骤如下（以1C为例）：

1）调节恒温箱为25℃，放入电池，静置1 h，先恒流（1C）充电将电池充至截止电压4.2 V，再恒压充电将电池充至截止电流1.5 A（0.05C）。

2）静置1 h，以1 C放电10 s，静置40 s，0.75 C充10 s，静置1 h。

3）每放电至指定的SOC，重复步骤2），直到截止电压为2.8 V。

图2表示25℃时不同放电倍率、SOC下的电池等效内阻。

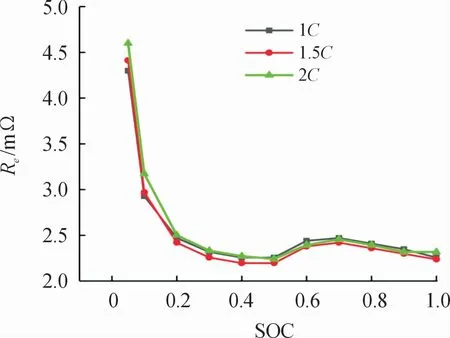
图2 25℃时不同放电倍率、SOC下的电池等效内阻曲线

根据图2测得的等效内阻值，通过拟合5阶多项式，得到不同放电倍率下Re随SOC变化的关系式：

1C放电倍率：

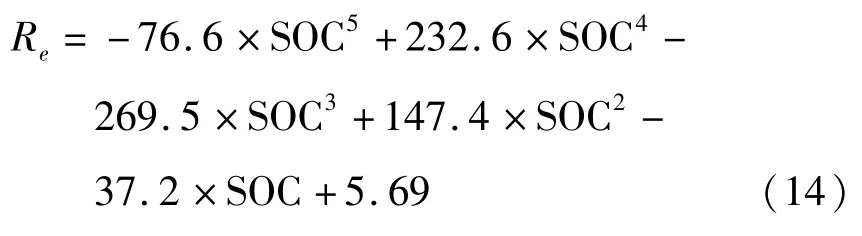
1.5 C放电倍率：

2C放电倍率：

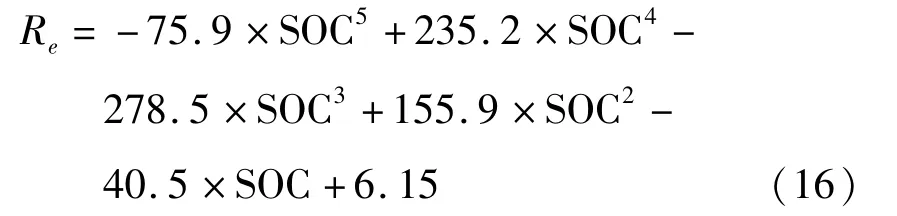
电池SOC和电流、时间的关系为

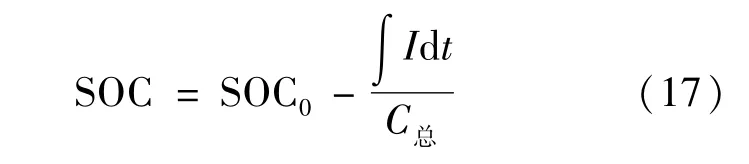
式中：SOC0为电池初始SOC值；I为放电电流（A）；t为放电时间（s）；C总为电池总电量（Ah）。

将式（8）（9）（14）～（17）代入式（3），即可得到不同放电倍率下随时间变化的内核生热速率。

1.4 仿真流程

方形电池极耳连接结构复杂，且极耳生热主要传递到上方壳体，所以省略了极耳及其连接结构，将整个电池看做一个整体，按实际尺寸建立图3所示的单体电池三维物理模型。同时极耳处电流度分布不均匀所以将理论计算得到的正负极耳处的生热速率按一定比列加载到正负极柱上。

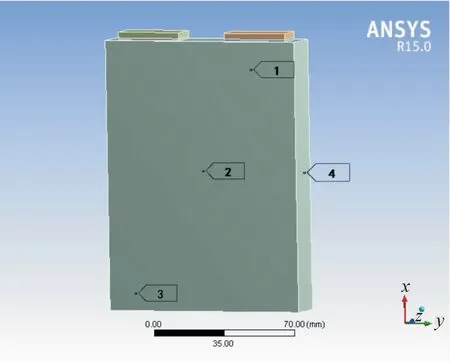
图3 单体电池三维物理模型示意图

采用Ansys workbench中的瞬态热分析模块模拟电池自然对流情况下的放电温升情况，具体设置如下：

1）添加材料，设置模型中各结构的材料属性。

2）均采用结构化网格。

3）设置边界条件：由于本文模拟的是自然对流仿真，故设置对流换热系数为8.5 W/（m2·K）；加载体热源的生热速率由模型内核区域加载式（3）根据不同放大倍率计算得到。

4）求解计算。

2 结果与讨论

2.1 实验设备

本文所使用的电池为30 Ah方形铝壳锂离子电池（额定电压3.7 V），正极材料为NCM523，负极材料为石墨；有关电池检测设备参数如表4。采用宁波拜特电池检测设备对电池进行充放电实验，采用热电偶采集电池表面温度，采用所亚特恒温箱控制环境温度。

2.2 实验结果及分析

如图4所示，选取电池表面4个点进行温度采集，为仿真结果提供验证数据，具体实验步骤如下：

1）调节恒温箱为25℃，放入贴好热电偶的电池，静置1 h。

2）对电池以（1C）恒流恒压充满电，截止电压为4.2 V，截止电流为0.05 C，静置1 h。

3）以1C倍率放电至截止电压2.8 V，静置1 h。

4）重复步骤2）和步骤3），将放电倍率分别调整为1.5 C、2 C。

表4 电池检测设备参数

图4 电池及其表面温度采集位置

图5 、6为采集到的温升曲线，从图中可知：

1）任意放电倍率下，相较于放电中期，放电初期和放电末期电池温升明显。其主要原因有两点：一是电池放电内阻值在SOC处于0.1～1时变化较小，在0～0.1时变化显著，所以放电末期产生大量不可逆热，导致此段区间内温升明显；二是根据测得的熵热系数值，放电中期，系数为正值，电池表现为吸热状态，所以此段期间温升相对平缓。

2）随着放电倍率增大，电池放电中期温升趋势更加陡峭。其主要原因在于，随着放电电流增大，由内阻造成的不可逆热对温升的影响远高于可逆热。

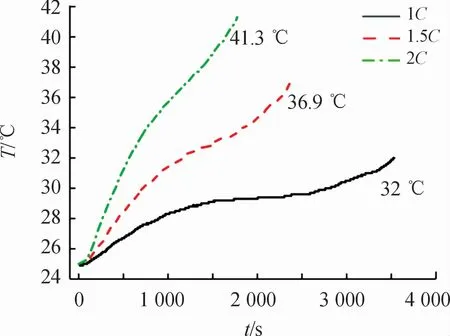
图5 电池不同倍率下的中心位置温升曲线

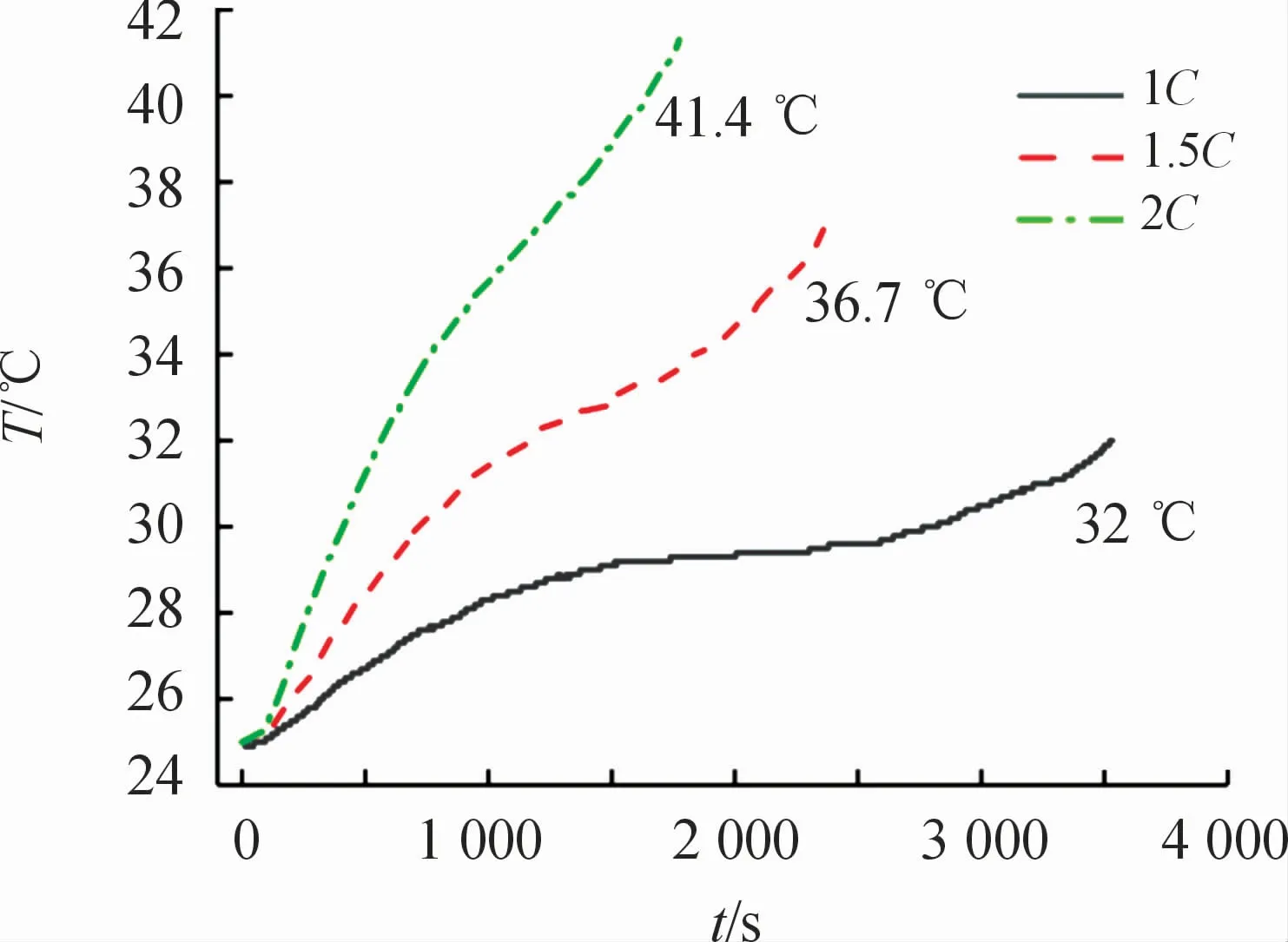
图6 电池不同放电倍率的多点平均温升曲线

2.3 仿真结果及分析

本文建立方形锂离子电池三维热物理模型，考虑到熵热系数不同的取值方式对仿真精度的影响。由于中心位置温升与4个位置点平均温升情况相似，所以将中心位置（2号位置）作为主要研究点。图7～9分别为采用变熵热系数与定熵热系数时，25℃自然对流条件下电池不同倍率放电结束时二号位置温升的仿真结果与实验结果曲线。从图中的曲线可以看出：定熵热系数仿真的结果不能有效地描绘出电池的温升趋势，在1C放电倍率下，仿真与实验结果差距显著。其原因在于：使用的电池熵热系数值偏大，1C放电倍率下，可逆热对电池温升影响十分显著，熵热系数的改变影响着可逆热的数值大小，定熵热系数仿真忽略了这一情况所以精度较低，而动熵热系数考虑到了熵热系数随SOC的变化，所以能够相对准确地描绘出温升趋势。

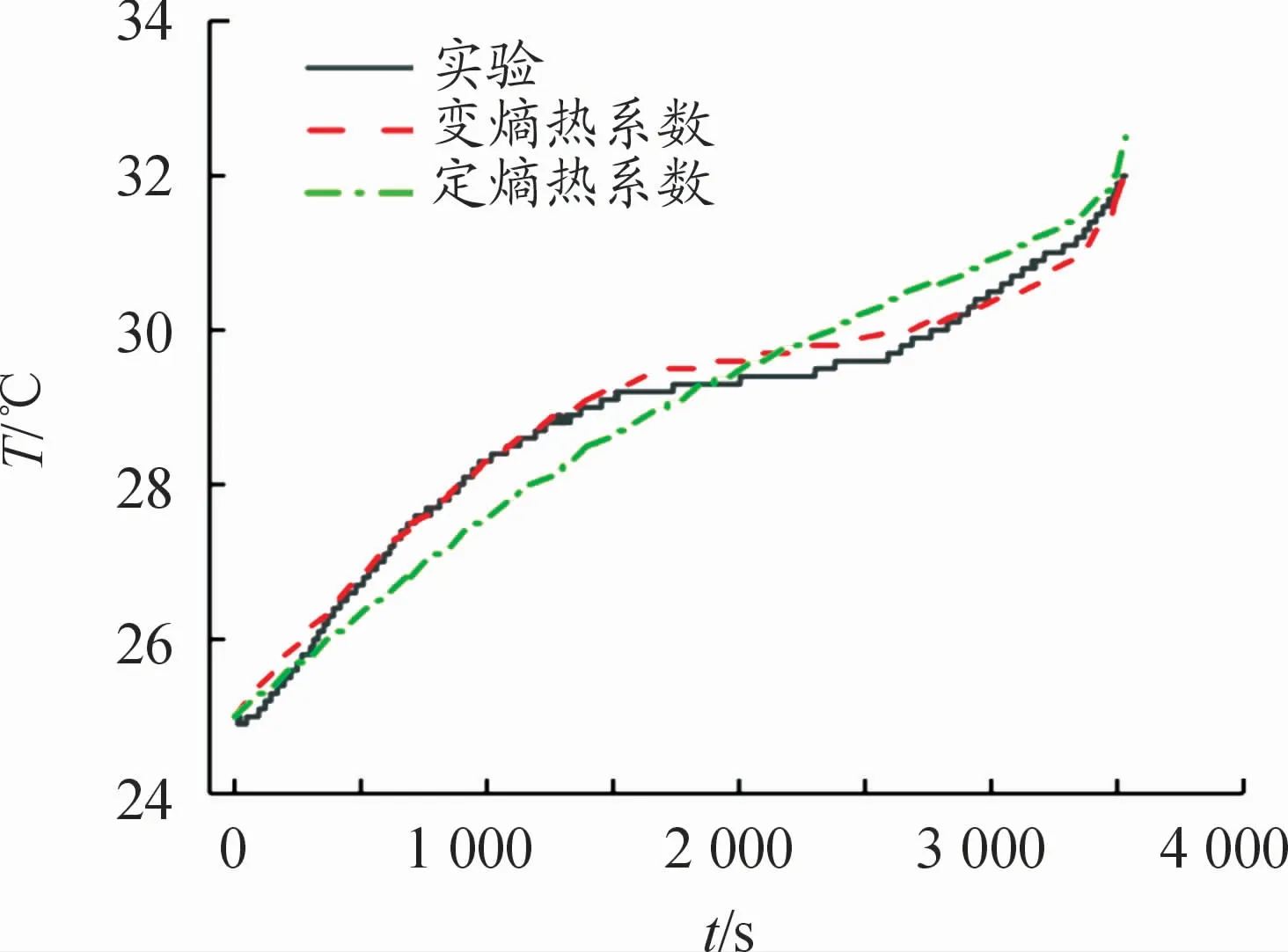
图7 1C倍率放电时实验与仿真温升曲线（2号位置）

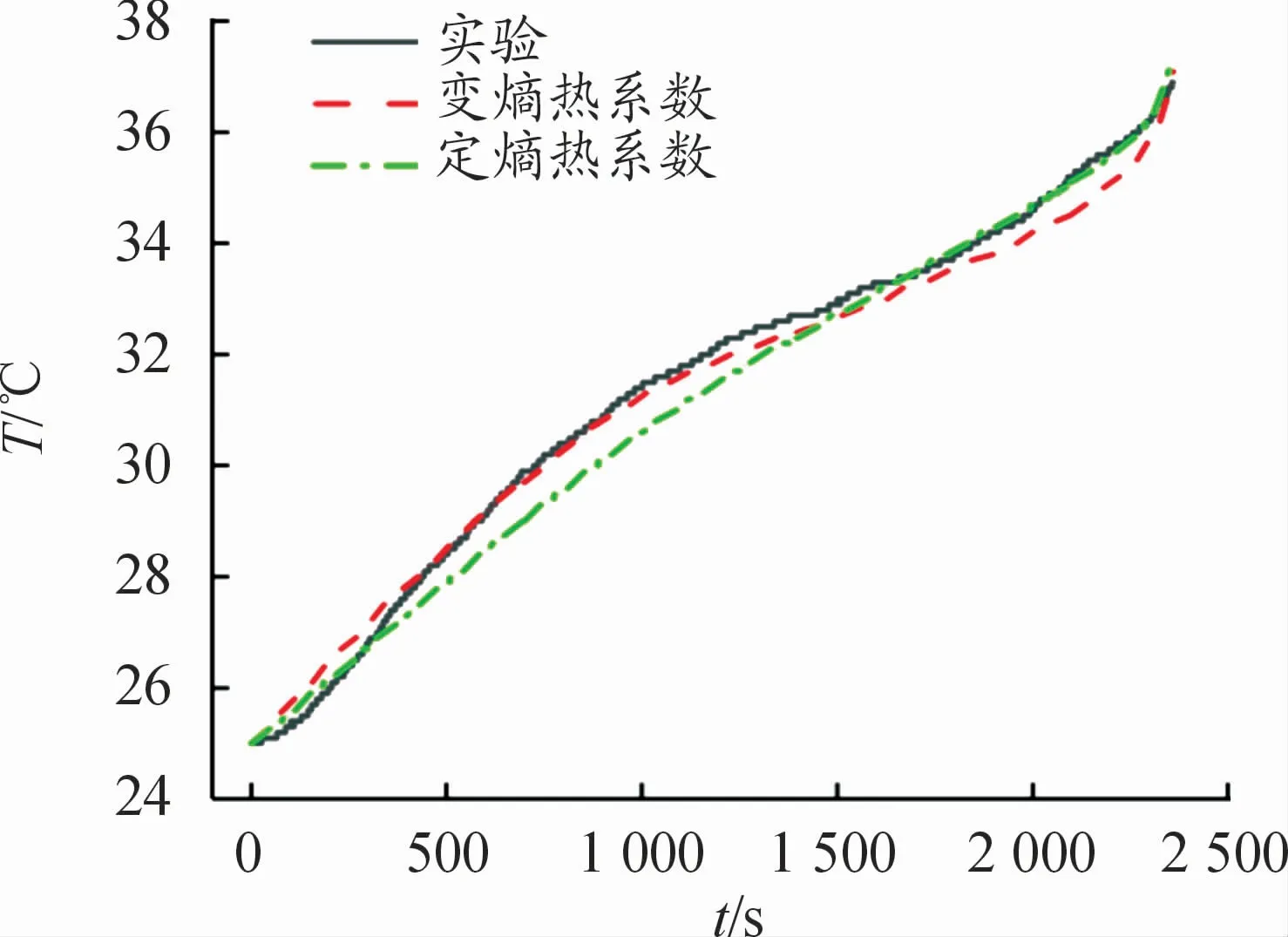
图8 1.5C倍率放电时实验与定熵热系数仿真温升曲线（2号位置）

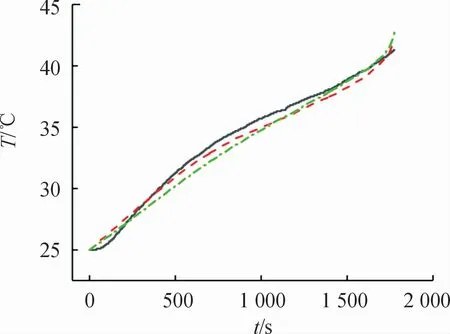
图9 2C率放电时实验与定熵热系数仿真温升曲线（2号位置）

为了能够更加直观地对比2种取值方式的仿真精度，引入均方根误差Rmse和最大误差emax这2个数学统计量来量化误差程度。均方根误差表示整个放电过程中每个数据采集时刻仿真结果与实验结果的误差均方根值；最大误差表示整个放电过程中所有数据采集时刻仿真结果与实验结果的误差最大值，计算公式为

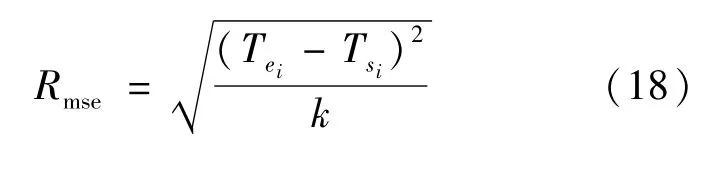
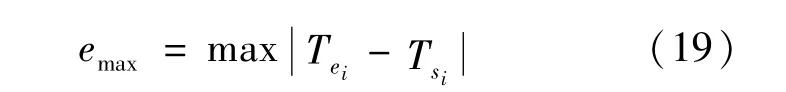
式中：Tei为第i个点的实验温度（℃）；Tsi为第i个点的仿真温度（℃）；k为总的数据采集点个数。

误差计算结果如表5所示。从表中可以看出：在1C、1.5C、2C放电倍率下，采用定熵热系数仿真结果与实验结果最大误差分别为0.80、0.90、1.40℃，均方根误差分别为0.46、0.46、0.75。采用动态变熵热系数仿真结果与实验结果的最大误差分别为0.40、0.70、1.00℃，与前者相比分别减小了50%、22%、29%，均方根误差分别为0.20、0.32、0.55，与前者相比分别减小了50%、30%、33%，通过对比可以看出，对于三元锂离子电池，采用变熵热系数仿真的精度明显高于定熵热系数。

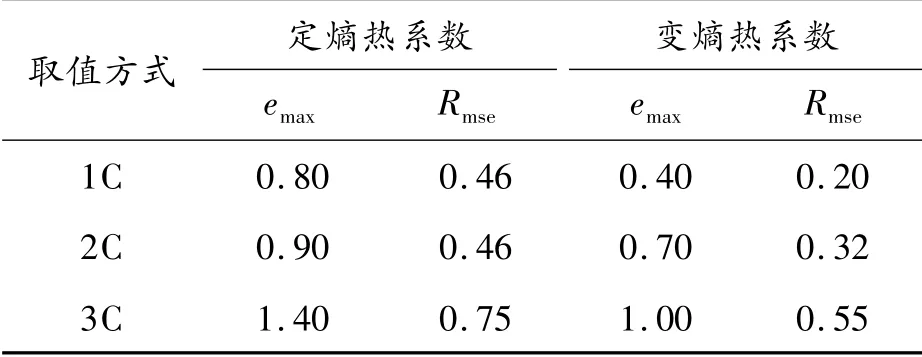
表5 2种简化方式仿真与实验曲线误差 ℃

3 结论

本文基于Bernadia生热速率模型，选取锂离子电池熵热系数作为研究对象，考虑到三元电池熵热系数的非平滑变化特性，提出了电池熵热系数的分段式表征模型。将所提出熵热模型应用于方形电池三维热物理模型中，仿真得到不同放电倍率下电池的温升。将所获取仿真结果与实验实测数据进行比较，结果表明：相较于传统定熵热系数，采取变熵热系数仿真精度更高，在1 C、1.5 C、2 C放电倍率下仿真与实验曲线最大误差分别减小50%、22%、29%，均方根误差分别减小50%、30%、33%。