最小二乘估计量优于工具变量估计量的一个充分条件

王义闹

(温州大学数理学院，浙江温州 325035)

考虑随机解释变量问题：

式中，b0,1b为常数，x为随机解释变量，u为随机误差项，x与u线性相关．

我们知道，对(x,u)的容量为n的简单随机样本

有

参数1b的最小二乘（OLS）估计量

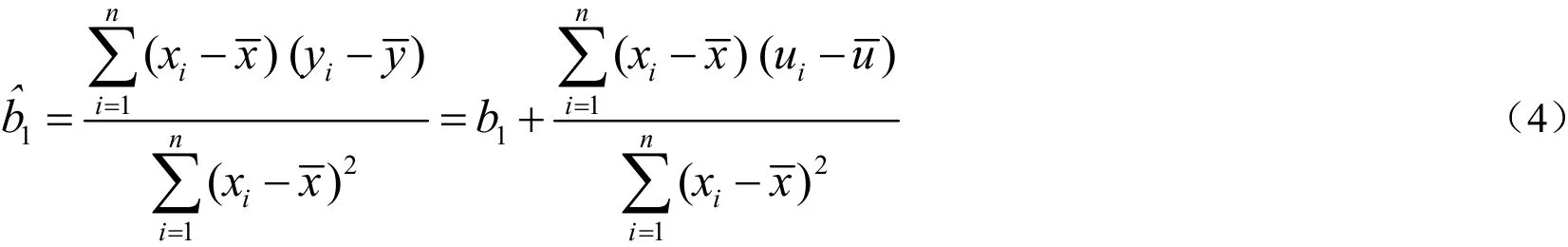
不是一致估计量；参数1b的工具变量（IV）估计量

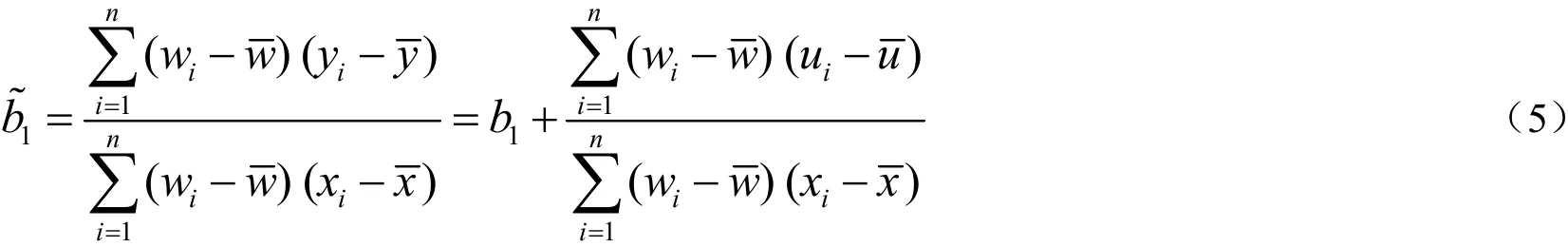
是一致估计量，其中w是x的工具变量[1]．因此，只要样本容量足够大，就一定有：

上述结论也意味着，样本容量不够大时，上式不一定成立．本文进一步给出了样本容量确定时，

成立的一个充分条件，即最小二乘估计量优于工具变量法估计量的一个充分条件．

1 工具变量法估计量与最小二乘估计量的误差分析

对x的任一工具变量w，参数1b的工具变量估计量

式中，

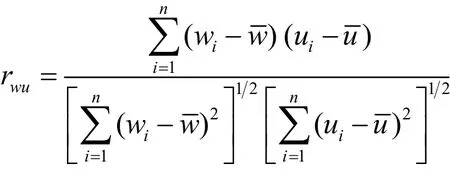
为工具变量w与随机误差项u的样本相关系数，

为工具变量w与随机解释变量x的样本相关系数．再记样本标准差

则由（8）式可见，参数1b的工具变量估计量的绝对误差为：

因此，当我们选取的解释变量的样本观察值越分散，工具变量与随机解释变量的样本相关系数的绝对值越大时，误差越小．

参数1b的最小二乘估计量为：

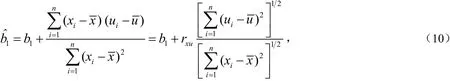
其中

为随机解释变量x与随机误差项u的样本相关系数，于是最小二乘估计量的绝对误差为：

故有下面引理1．

引理1 当

时，工具变量估计量的绝对误差小于最小二乘估计量的绝对误差，否则，最小二乘估计量更好．

2 工具变量估计量的绝对误差较小的概率

1915年Fisher找到了样本相关系数的精确分布[2]：

在X,Y服从二维正态分布，相关系数的假设下，当样本容量n≥3时，样本相关系数rXY的概率密度为：

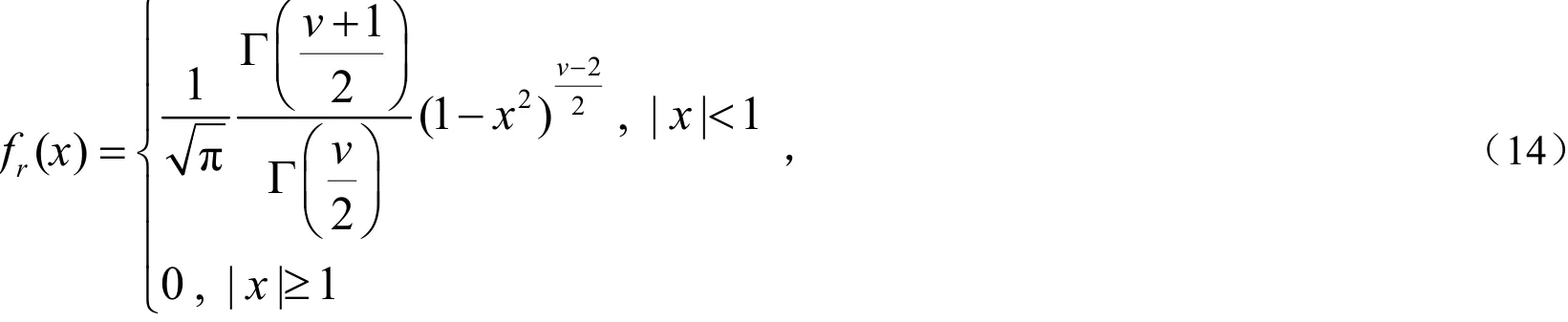
其中v=n-2是自由度．

据此对不同样本容量n，可求得0.75分位数x0.75使

定理1 设工具变量w与随机干误差项u服从二维正态分布样本容量则工具变量估计量的绝对误差小于OLS估计量的绝对误差的概率为：

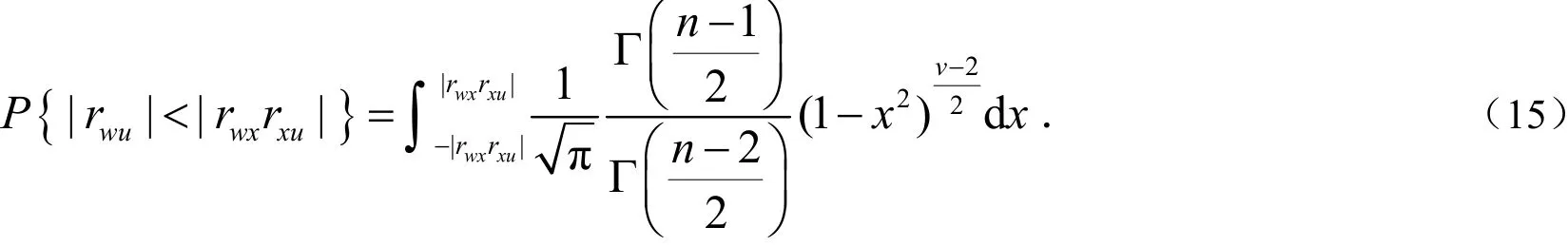
证明：由于工具变量w与随机干扰项u服从二维正态分布，样本容量n≥3，且工具变量w与随机干扰项u不相关，所以样本相关系数rwu的概率密度为（14）式，再由引理1知，工具变量估计量的绝对误差小于OLS估计量的绝对误差的概率为：

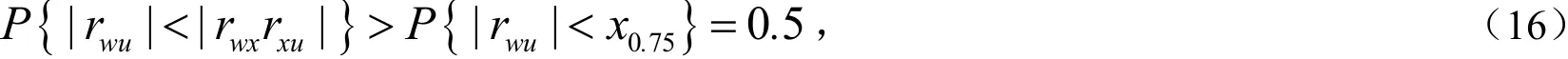
再由（13）式可知，上式意味着工具变量估计量的绝对误差小于OLS估计量的绝对误差的概率大于0.5；当时，

上式意味着OLS估计量的绝对误差小于工具变量法估计量的绝对误差的概率大于0.5．

为查阅方便，将根据（14）式计算的样本相关系数的0.75分位数x0.75列于表1．

表1 样本相关系数的0.75分位点

由定理1及表1可见，当样本容量为10时，如果|rwxrxu|大于0.242，则工具变量法估计值优于OLS估计值的概率大于0.5，我们应该应用工具变量法估计参数；如果|rwxrxu|小于0.242，就应该用最小二乘法估计参数．而当样本容量为100时，哪怕解释变量与随机干扰项u的样本相关系数小到只有0.1，只要|rwxrxu|大于0.068，应用工具变量法估计参数仍然优于最小二乘法．

在实际问题中，随机干扰项u的取值观察不到，无法验证是否成立．但是，由于可以由观察值计算，如果就必有应该用最小二乘法估计参数．这个结论就是定理1的一个推论：

推论1给出了一个判断最小二乘法估计量优于工具变量法估计量的充分条件，实际问题中这一充分条件是否满足，很容易通过计算随机解释变量与其工具变量之间的样本相关系数判断．