关于二维正态分布的一个教学注记
2016-08-15吕东风广东技术师范学院天河学院通识教育学院
吕东风(广东技术师范学院天河学院通识教育学院)
关于二维正态分布的一个教学注记
吕东风
(广东技术师范学院天河学院通识教育学院)
利用二维正态分布定义中的一个基本事实,简单地说明了两个正态分布的联合分布不一定是二维正态分布,指出了教材中一个性质的不足之处。
二维正态分布;相关系数;数学问题
众所周知,二维正态分布是概率论中非常重要的一种分布,其性质也是很重要的,但很多教材在讨论两个正态分布的联合分布是不是二维正态分布这个问题时,要么就是说得不是很清楚,要么就是没有给出例子,要么就是给出的例子比较复杂,其实只要注意到二维正态分布定义中的一个基本事实,这个问题就可以说得很清楚。
首先,给出二维正态分布的定义:如果二维随机变量(X,Y)的概率密度函数为:
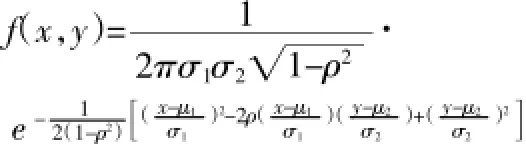
其中μ1,μ2,σ1,σ2,ρ均为参数,且σ1>0,σ2>0,<1,则称(X,Y)服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布,记作(X,Y)(μ1,μ2,σ1,σ2,ρ)。
经过讨论,发现如果(X,Y)服从二维正态分布,那么两个分量X,Y都服从一维正态分布,而且参数ρ就是两个分量X,Y的相关系数,它是不能等于1和-1的,也就是说(X,Y)服从二维正态分布的前提是:两个分量X,Y是正态分布,而且它们的相关系数不是1和-1。
如果二维随机变量(X,Y)的两个分量X,Y是同一正态分布,都是X,那么(X,Y)就不服从二维正态分布,因为两个分量的相关系数是1。这样我们就很容易解释,为什么两个分量是正态分布,但它们的联合分布不一定是正态分布。
另外,一些教材中往往给出二维正态分布的这样一个性质:
性质:若(X,Y)服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布,那么(aX+bY,cX+dY)服从二维正态分布。
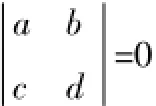
[1]魏宗舒.概率论与数理统计教程[M].高等教育出版社,2004-04-01.
[2]盛骤.概率论与数理统计[M].高等教育出版社,2008-06-01.
[3]陈希孺.概率论与数理统计[M].国防工业出版社,2010-01-01.
·编辑 李建军
A Note on Two Dimensional Normal Distribution
Lv Dongfeng
By using a basic fact in the definition of two-dimensional normal distribution,it is simple to show that the joint distribution of the two normal distributions is not necessarily a two-dimensional normal distribution,pofnted out the deficiency of a property in the textbooks.
two-dimensional normal distribution;correlation coefficient;maths problem
