基于IGWO的燃料电池汽车模糊控制能量管理策略

周健豪，顾 诚，刘 军，海 滨，赛影辉

（1.奇瑞汽车股份有限公司，安徽 芜湖 241009；2.南京航空航天大学 能源与动力学院，南京 210016）

质子交换膜燃料电池（PEMFC）被普遍认为是最具潜力的车用储能系统之一［1-4］。然而，燃料电池系统存在成本高、反应慢、无制动时的再生能量回收、无法跟踪快速负载变化，车辆运行中的负载需求波动可能导致燃料电池膜上的燃料不足、流动、膜干燥和压力不平衡，从而损坏燃料电池堆并降低其寿命［5-8］。由于加速度、路面和交通条件的变化，汽车的功率需求发生显著变化，车辆的不稳定运行可能不适合使用单一的燃料电池系统［9］。因此，将燃料电池系统经常与电池、超级电容等相结合组成混合储能系统（HESS），不仅能降低系统成本，改善整车系统的动态性能，提高燃料电池的使用寿命，而且由于再生制动能量的回收提高了燃料经济性［10-11］。

目前，燃料电池混合动力汽车（FCHEV）的能量管理策略主要有模糊逻辑、动态规划、神经网络和小波变换等。模糊控制由于其鲁棒性强、实时性好等优点，应用尤其广泛［12-13］。Kim M等［14］提出了一种基于模糊控制的燃料电池混合动力汽车能量管理策略，显著提高了复合电源的工作效率。王跃飞等［15］综合考虑复合电源状态信息和驾驶员意图设计了一种新型双层模糊控制器，有效提升了汽车经济性。

上述建立能量管理策略的方法仅依靠专家的经验和不断的调试，无法定义控制目标并且信息简单的模糊处理将导致系统的控制精度降低。灰狼优化算法（GWO）是一种比较新颖的全局优化算法，该算法具有结构简单、需要设置的参数少和在实验编码中容易实现等优点［16-17］。

本文采用模糊控制能量管理策略，利用灰狼优化算法对模糊控制隶属度函数进行调整。另外，灰狼优化算法也存在求解精度不足和容易陷入局部寻优的缺陷，DORIGO M等［18］提出一种动态种群思想，本文使用这种思想对灰狼优化算法进行改进来避免算法局部寻优，最后将改进的灰狼优化算法（IGWO）应用于模糊控制策略中。在本文中，选用2个循环行驶工况（FTP72工况和NEDC工况）进行仿真测试模拟。

1 复合电源能量系统的建模

图1给出了燃料电池混动汽车系统结构示意图，其中电机作为该对象的动力传输装置；燃料电池、电池作为能量源。DC/DC变换器可变换燃料电池输出电压至母线电压，能量管理器进行功率分配。

图1 燃料电池混动汽车系统结构示意图

1.1 整车动力学建模

混合动力汽车在行驶时，受到空气阻力、坡度阻力、滚动阻力等外力作用，其动力学方程可描述为：

式中：Pt为汽车功率需求；v为汽车当前车速；m为整车质量；μ为滚动阻力系数；ρ为空气质量密度（kg/m3）；A为迎风面积（m2）；Cd为空气阻力系数；a为汽车当前加速度；θ为路面与水平面的夹角。

1.2 燃料电池模型

燃料电池系统的输出功率Pfc_req等于燃料电池系统功率Pfc与附件消耗功率Pfc_aux之差，而燃料电池系统功率等于输出电压Ufc与输出电流Ifc乘积：

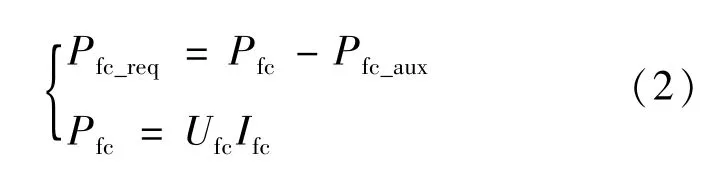
燃料电池的氢耗量与输出电流相关，表达式为：

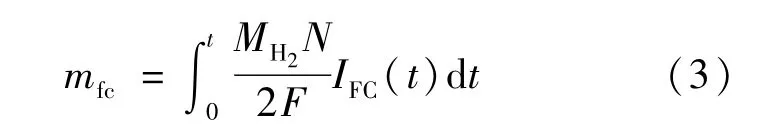
式中：mfc为氢气的消耗量；MH2为氢气摩尔质量；F为法拉第常数；N为燃料电池的单电池数目。燃料电池附件消耗功率Pfc_aux可以表示为燃料电池系统功率多项式函数，其拟合式如式（4）所示：

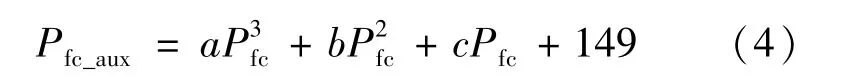
式中：a=3.41×10-11，b=-1.7×10-6，c=4.99×10-2，拟合方差R2=0.92。

图2为燃料电池系统的效率和电流与功率的关系曲线，可以看出燃料电池效率随FC功率的提高先迅速上升再缓慢下降。

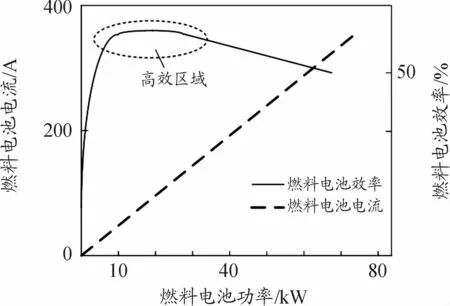
图2 燃料电池效率和电流-功率曲线

1.3 锂电池模型

将电池简化成一个电压源和内阻串联的等效电路。锂电池输出功率可以表示为

锂电池的荷电状态SOC采用安时法计算，公式为：

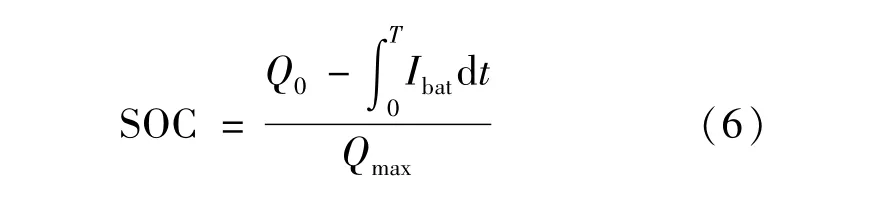
式中：Q0为锂电池的初始容量；Qmax为锂电池最大容量。

电池的工作状态与电池的SOC值有关。图3表示内阻与电池SOC值的关系。

图3 电池系统内阻的变化关系曲线

1.4 电机模型

电机既可作为电动机实现驱动供能，又可作为发电机实现再生制动功能。电机效率ηm可以根据电机转速和转矩需求查表得到，公式如下：

式中：nm为电机转速；Tm为电机转矩。

电机机械输出功率Pm与电功率Pe的关系为：

其中，电机作为电动机工作时，转矩为正；作为发电机工作时，转矩为负。

建模过程中涉及到的关键电器元件的参数，如表1所示。

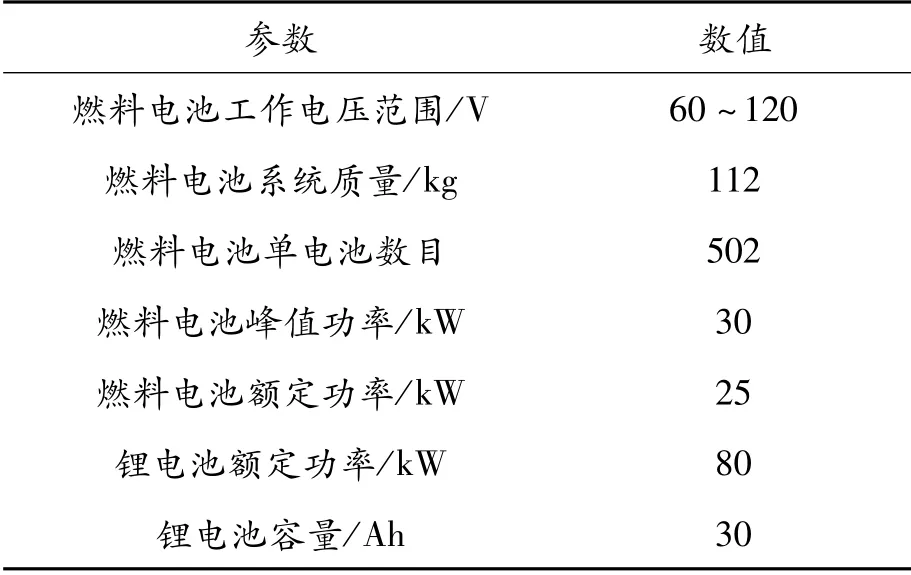
表1 关键电器元件的基本参数

2 考虑燃料电池效率的模糊控制策略

2.1 隶属度函数设计

常规的燃料电池-锂电池混合动力汽车模糊逻辑能量管理策略只考虑功率需求和锂电池的SOC作为模糊控制器的输入变量，再根据制定的规则进行能量分配，这种策略没有考虑到燃料电池的放电特性。如图2所示，根据燃料电池效率-电流-功率曲线，在低功率时，燃料电池效率随燃料电池功率上升而迅速上升，在功率达到15 kW左右时，燃料电池效率达到峰值，之后随着燃料电池功率的上升缓慢下降。由此可知，燃料电池功率与放电效率相关，从而影响燃料电池氢耗量。因此，将燃料电池系统效率添加为模糊逻辑输入变量［19］。由于燃料电池系统效率又与其输出电流相关，故将燃料电池的输出电流也添加为模糊逻辑的输入变量作为功率分配依据。

本文共有4个模糊输入量，分别为功率需求Pload、锂电池SOC、燃料电池电流Ifc和燃料电池系统效率η，以及一个模糊输出量燃料电池的功率输出Pfc。功率需求Pload划分为3个模糊子集，为｛L，M，H｝，依次分别表示低、中、高功率区间；同理，SOC、燃料电池效率η和功率Pfc均划分为3个模糊子集｛L，M，H｝，依次代表低、中、高区域；Ifc划分为2个子集，｛L，H｝，分别表示燃料电池低、高电流输出区间。考虑效率的模糊逻辑的输入输出的隶属度函数如图4所示。

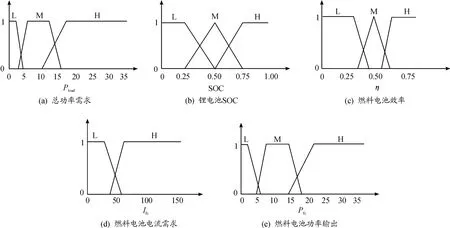
图4 模糊逻辑隶属度函数曲线

2.2 燃料电池效率对比

基于FTP72工况对普通模糊控制策略和考虑效率后的模糊控制策略进行了模拟。图5表示了这2种控制策略下工作点分布情况。可以看出，考虑效率的模糊控制可以使燃料电池工作点更聚集在高效区域，显著提高燃料电池的放电效率，提升系统的经济性和使用寿命。

然而，由于模糊控制本质是基于规则的策略，主要依赖专家经验，缺乏系统性，无法定义控制目标。因此，引入了灰狼优化算法（GWO）对模糊逻辑规则进行优化。

图5 2种控制策略工作效率点分布示意图

3 基于IGWO的模糊控制策略优化

GWO算法来源于灰狼种群等级制度和捕食行为，具有结构简单、超参数少和编码容易等优点。本文的优化目标是降低车辆在整个行驶里程中的等效氢耗量，即燃料电池的氢耗量加上锂电池的间接氢耗量，故目标函数即适应度函数设置如下：

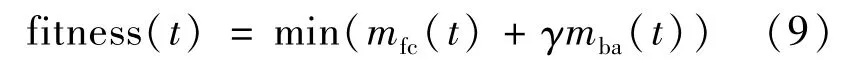
式中：γ为等效因子。

为了得到优化问题的可行解，必须满足如下约束条件：

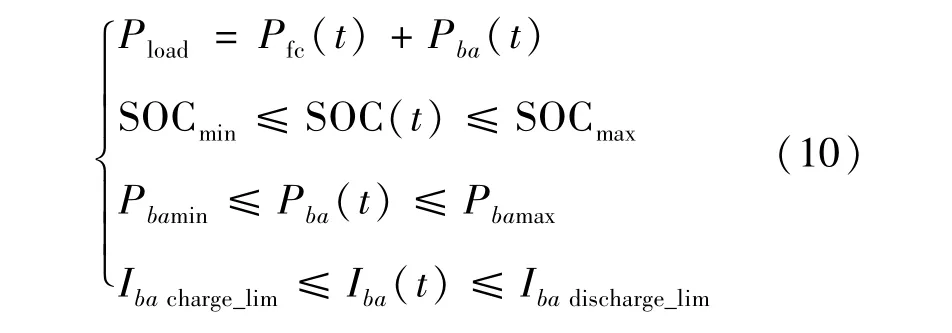
GWO主要模拟了狼群捕食猎物的过程，其对应的数学模型包括以下几个部分：

1）等级分层：构建灰狼社会等级分层模型，计算种群中每个个体的适应度，将适应度最高的3个个体标记为α、β、δ，其余的狼标记为ω。灰狼优化的优化过程主要由每一代种群中的α、β、δ狼来指导完成。

2）包围猎物：灰狼群体习惯从较远的位置发起进攻，目的是包围目标猎物，令猎物不能逃脱，将包围目标猎物的过程刻画为数学模型［20］：

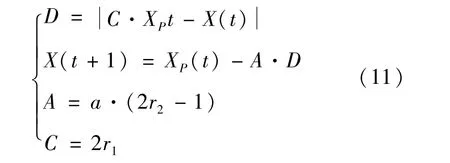
式中：t为当前迭代次数即整个捕猎包围过程迭代的总次数；A和C是协同系数向量代表距离系数；Xp（t）代表猎物所处方位；X（t）代表灰狼当前所处方位，在整个迭代过程中，a由2线性降到0，r1和r2是［0，1］范围内的随机数。

3）狩猎：在现实自然环境灰狼群体狩猎的过程中，猎物的详细方位是可以被灰狼群体所感知到的。本文规约猎物所处的方位为α、β及δ所处的方位，α、β、δ会依据自己所处的方位，指引其他个体狼位置的更新。其方位更新方式如下：

式中：X1、X2和X3是根据2）中的公式将α、β、δ狼赋值给Xp后，得到的全局搜索后的解空间向量，其余个体狼根据这3个解向量更新自己的位置。

4）攻击猎物：改变a的值，即可完成模拟灰狼群体攻击猎物的过程。根据2）中的公式可知，a的值的减小也会引起A值随之减小，A的取值如果处于［-1，1］范围内，那么个体狼将随时处于猎物附近，寻找攻击时机，即|A|＜1，灰狼群体将会朝着猎物所处的方位进行转移，以此来比喻猎物受到了狼群的攻击，进攻猎物通过这样的方式即可被模拟出来。

5）寻找猎物：灰狼群主要依赖α、β、δ狼的位置信息来寻找猎物，先分散地去搜索猎物位置信息，再集中起来攻击猎物。A的取值在［-1，1］范围内时，灰狼群体意图靠近猎物，猎物就会受到灰狼群体的攻击。如果|A|≥1，那么猎物就不会受到灰狼群体的重视，灰狼群体会分散在各个区域搜索猎物，伺机寻找附近有没有适应度更高的猎物。

GWO在迭代完一次后，其余个体狼位置只由3匹狼（α、β、δ）引导，很容易陷入局部寻优。为了解决这种缺陷，提出基于动态种群思想的改进灰狼优化算法（IGWO），即：在完成每次迭代后，动态种群算法会改变狼群中适应度较低的个体狼的位置信息并进入到下一次迭代中。

式（13）表示动态种群算法的过程，其中每个式子都有1/4概率被选中执行：

式中：r是介于［0，1］范围内的随机数，μb和lb对应为搜索空间的上边界和下边界。

具体而言，IGWO算法包含如下几个步骤：

步骤1初始化灰狼种群。

步骤2计算狼群中个体狼的适应度值。

步骤3选出适应度最高的3匹个体狼，定义它们为α、β、δ狼。

步骤4根据式（11）（12）确定其余个体狼的位置。

步骤5每只个体狼，会被重新计算各自的适应度值。

步骤6根据式（13），对较低适应度值的个体狼进行重新定位。

步骤7判断迭代次数是不是到了最高次数，假如是最大次数，那么停止迭代，猎物所在的方位即当前α狼所在的方位；如果迭代次数没有达到最大迭代次数，那么返回到步骤2。

基于IGWO的模糊控制策略优化求解流程框图，如图6。

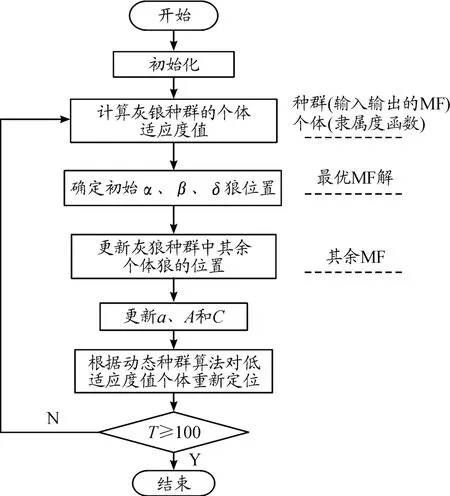
图6 IGWO优化模糊逻辑流程框图

4 仿真结果分析

根据上文所述能量管理策略，选择FTP72和NEDC工况进行仿真验证。仿真结果如下：图7为FTP72工况下，SOC初始值为55%时4种策略的功率分配情况。相应地，图8是在NEDC工况下的功率分配情况。综合来看，4种控制策略均满足整车动力性需求，其中，可以明显看出前2种模糊控制策略由于基于人工设定的规则，其燃料电池功率大多在固定值工作，而基于灰狼优化的模糊控制策略的燃料电功率根据总功率需求实时变化。另外，由于在设计模糊控制规则时，遵循原则：当总需求功率为高时，若蓄电池SOC为低或中区间，燃料电池会承担更多的功率分配需求，这从一定程度上消除了电池瞬间输出功率过大、大电流放电现象，避免对电池的损伤。

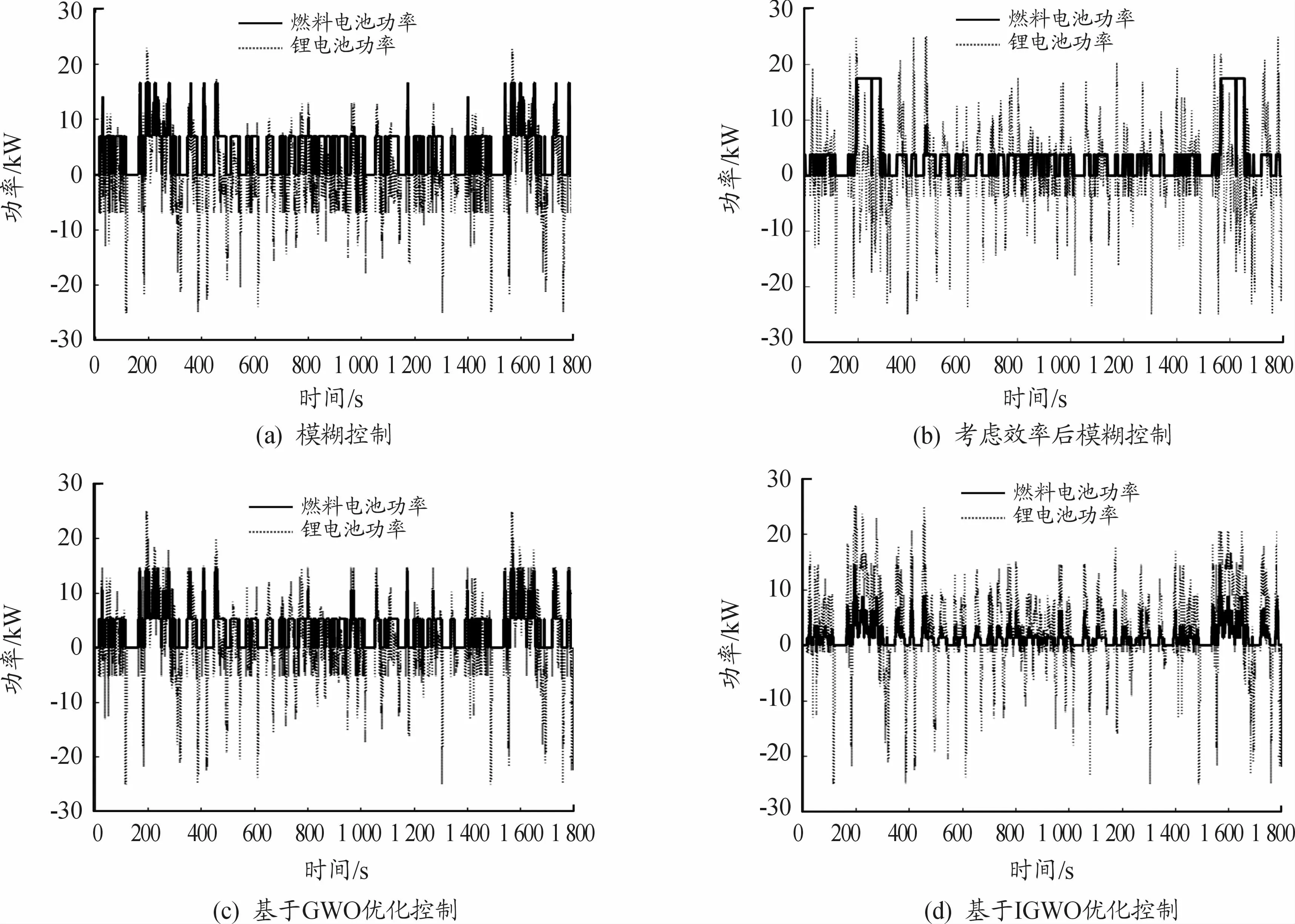
图7 FTP72工况下4种控制策略的功率曲线

图8 NEDC工况下4种控制策略的功率曲线

氢耗量的累积变化是体现控制策略经济性最重要的指标。图9为2种工况下蓄电池SOC的变化走势曲线，可以看出4种策略的SOC都落在［48，56］的稳定区间内。图10为4种控制策略分别在FTP72和NEDC工况下总等效氢耗量的累积变化图。可以看出，在FTP72工况下，由于需求功率大，普通模糊控制策略和考虑效率的模糊控制策略总等效氢耗量相差不大，后者较前者降低了8.4%。2种基于灰狼优化的控制策略的总等效氢耗量较前2种显著降低，其中，基于灰狼优化的控制策略和基于IGWO的控制策略的氢耗量较普通模糊控制策略分别降低了25.2%和62.6%。在NEDC工况下，4种控制策略的总等效氢耗量累积逐渐降低，后3种控制策略的氢耗量较普通模糊控制策略分别降低了22.5%、49%和68.6%，经济性逐渐提升。综合来看，基于IGWO优化的控制策略的总等效氢耗量显著低于前3种模糊控制策略。

图9 4种策略的蓄电池SOC变化曲线

图10 4种策略的总等效氢耗量累积变化曲线

5 结论

提出了一种基于模糊逻辑和改进灰狼优化的燃料电池混合动力汽车能量管理策略。燃料电池和动力电池共同满足基本负载需求，并且针对复合电源系统的氢耗、燃料电池效率等方面对能量管理策略进行了改进。仿真结果表明：所有的控制策略均可满足负载需求，并适用于不同工况，锂电池SOC可稳定在均衡区间。综合4种策略，其优劣取决于经济性。通过对比分析，发现：普通模糊控制策略、考虑燃料电池效率的模糊控制策略、基于GWO的模糊控制策略以及基于IGWO的模糊控制策略的燃料经济性逐步提升。其中，基于改进的灰狼优化的模糊控制策略经济性提升最为显著。