基于多重同步挤压变换与深度脊波卷积自编码网络的滚动轴承故障诊断
2021-06-10赵志川陈志刚夏建强
赵志川,陈志刚,2,何 群,张 楠,2,夏建强
(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.北京市建筑安全监测工程技术研究中心,北京 100044;3.安徽省春古3D打印智能装备产业技术研究院有限公司,安徽 芜湖 241000)
作为机械设备中最重要的部件之一,滚动轴承在功率传动过程中发挥着重要的作用,其运行状态会显著影响机械设备的工作性能。优质的运行状态不仅能保证工业生产的经济效益,更意味着隐患风险的降低,是设备安全运行的重要保障。因此,准确提取滚动轴承的故障信号并进行研究分析,对诊断轴承不同类型的故障有重要作用。
轴承发生故障时,其振动信号中往往隐含着丰富的故障信息。然而,采集到的故障信号本身往往不是线性平稳的。由于时频域分析方法能同时提供非平稳振动信号在时域和频域的局部化信息,因而在轴承故障诊断中得到广泛应用[1]。目前传统的时频域分析方法主要包括短时傅里叶变换、S变换、小波变换[2]等。傅里叶变换等方法在处理非平稳性信号时能够有效地提取信号频域内的特征信息。但是,它们的能量聚集性特别差,时频谱发散严重,且不具有自适应性。经验模态分解是一种自适应的信号处理方法,但其在信号处理与应用方面也存在端点效应以及模态混叠等一系列问题[3]。Daubechies等[4]提出了同步挤压变换(SST),提高了能量的聚集性,并成功地应用于信号识别[5]、轴承等机械零件的故障诊断[6]等领域。但是SST对噪声敏感,并且不适合处理强调频信号。于刚等在高阶SST[7]的基础上提出了多重同步挤压变换[8],该方法基于同步挤压变换,采用迭代重分配过程逐步集中模糊传递函数能量,同时保持了信号重构能力。在处理强时变信号以及噪声信号中取得了良好的效果。上述方法能够很好地进行故障特征的提取,然而,实际诊断中,往往还需要人工进行故障信息的特征提取以及故障类型的识别分析,效率不高。近年来,基于深度学习的智能诊断方法逐渐兴起。
在故障的智能识别方面,ANN和SVM是较为流行的2种传统智能识别方法。并在轴承的智能故障识别中得到了一些应用[9,10],但是它们均存在着维数灾难等问题。深度学习克服了浅层模型的缺陷,并大幅度应用于轴承的故障诊断领域中[11],但目前大多数有关深度学习的故障诊断研究只考虑到信号的时域或频域等单一信息,难以建立故障情况与输入之间的映射关系。陈志刚等[12]提出了一种基于深度脊波卷积自编码网络的故障识别方法,避免了复杂的人工提取特征过程,且该模型的故障识别能力优于浅层人工神经网络等方法,适用于故障识别领域。
基于此,本文提出了一种基于多重同步挤压变换与深度脊波卷积自编码网络的方法,对滚动轴承的故障振动信号进行特征提取与故障识别,并通过实验对提出的方法进行研究分析。
1 多重同步挤压变换
对一个单分量信号:
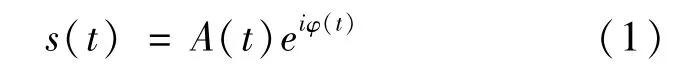
进行STFT变换,在极短的时间u∈[t-Δt,t+Δt]中,存在ε足够小,使得对于任意t,都能满足在此基础上使用泰勒展开,将u指向t,忽略泰勒展开的最终的叠加项,可以得到A(u)=A(t)以及φ(u)=φ(t)+φ′(t)(u-t)。
基于此,式(1)所示的单分量信号可以表示为:
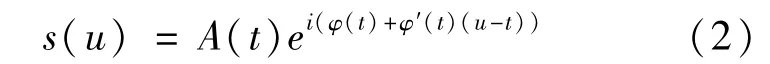
对其进行STFT,得到的结果为:
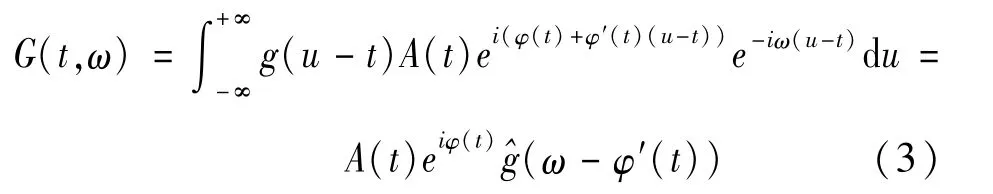
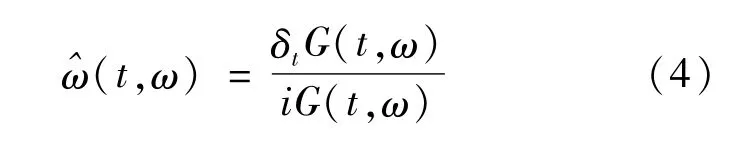
可以通过STFT的结果变换得出。
对于弱时变信号,预估的瞬时频率^ω(t,ω)与原始信号近似相同,SST使用了一个频率重分配的算子来聚集传播的时频系数,该算子表示为:
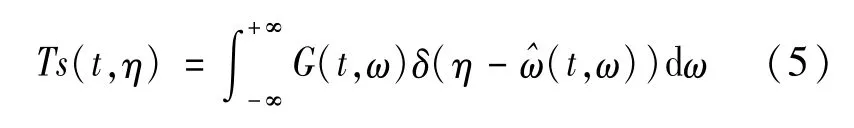
SST通过式(5)将每个模态的STFT结果中的能量集中压缩在了瞬时频率附近。
MSST主要就是对SST中的重分配算子进行多次的迭代,先对SST中的重分配算子进行2阶SST变换,可得:
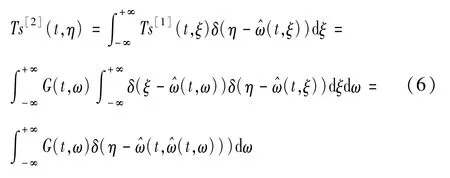
在2阶变换中预估瞬时频率,预估值为:
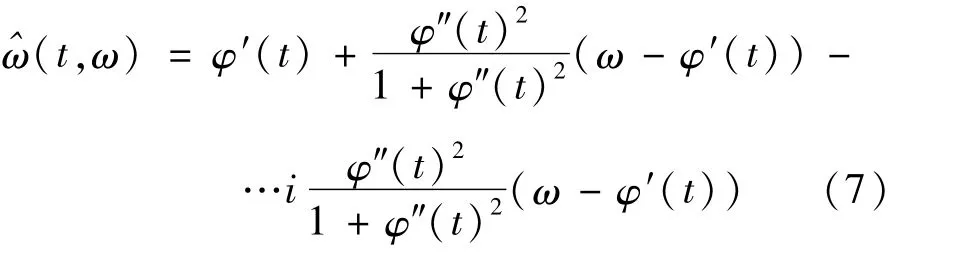
忽略式(7)中的复值,取实部作为瞬时频率预估值,通过进一步的改写,可以得到MSST的第2阶变换的瞬时频率估计值为:
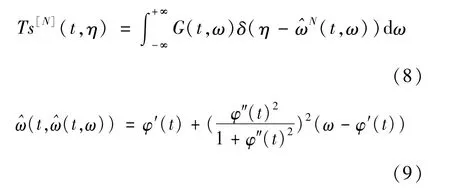
将重分配算子以及瞬时频率预估值推导至N阶,结果如下:
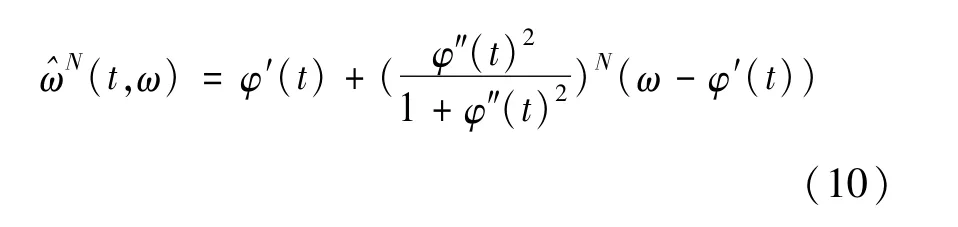
在每次的迭代后,MSST都构造了一个新的瞬时频率预估值^ω(t,^ω(t,ω))来重新分配模糊STFT能量的分配结果,针对预估值进一步预估瞬时频率,最终即可完成高阶的SST转换。
为了验证该方法对信号的处理能力,采用实验仿真的方式对该方法进行检验研究,假设一个强时变信号为:
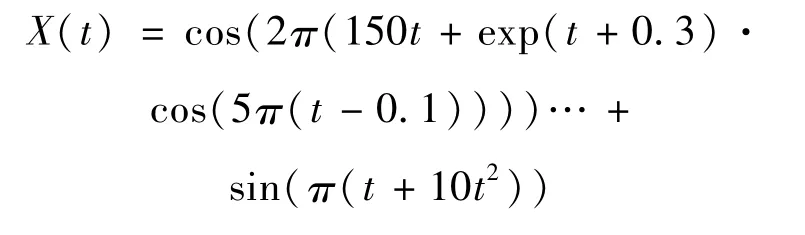
对该信号分别采用SST以及MSST变换处理,MSST设置为进行6次SST,其结果的时频图分别如图1、图2所示。
图1、图2中左图表示强时变信号通过不同方法变换处理后的结果,右图是左图的局部放大。从图1、图2中可以看出,2种方法都能得到大致的能量分布结果,但SST处理完后的信号能量发散较为严重,难以辨别能量集中的主要位置,而MSST处理完后的能量分布较为集中,局部放大图更是清晰地反映出了这一点。
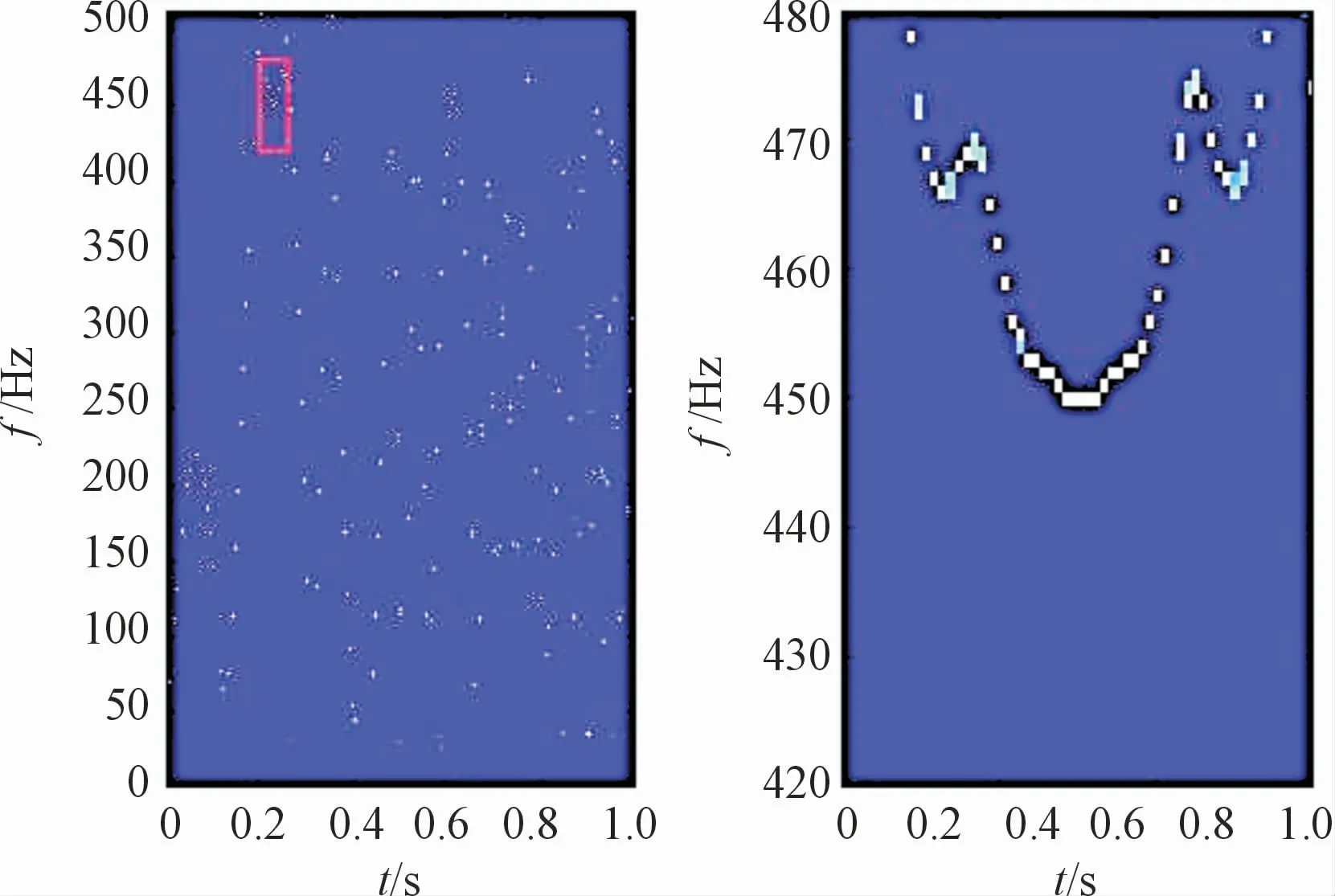
图2 强时变信号MSST结果
为了验证该方法对信号的重构能力,假设一个多分量信号为:
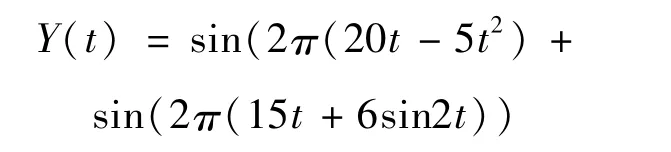
这个信号由2个单分量信号构成,2个信号交叉于1~2 s处,真实的信号构成与STFT处理结果如图3所示,将信号经过SST,设定为6次SST的MSST处理完后的结果如图4、图5所示。
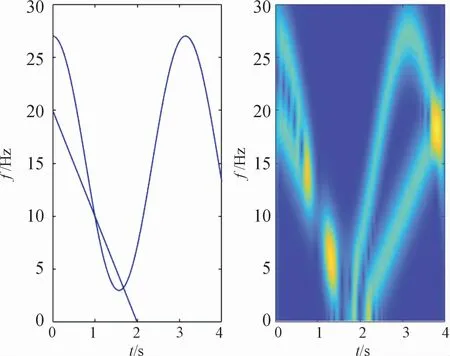
图3 原始信号瞬时频率及STFT结果
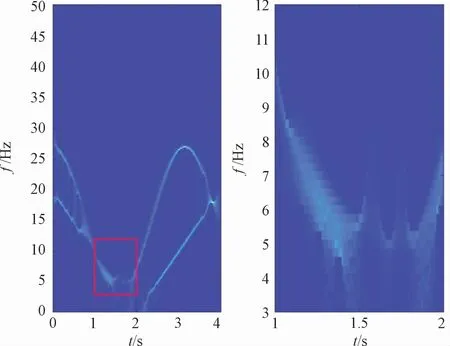
图4 多分量信号SST结果
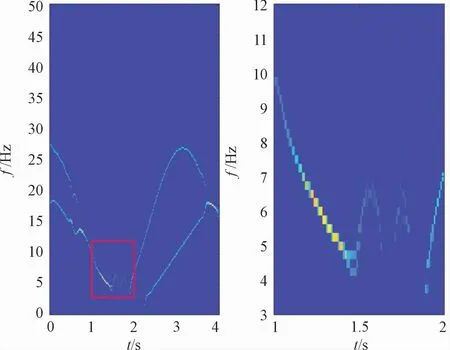
图5 多分量信号MSST结果
包含MSST在内的变换方法处理完后,时频结果均存在交叉干扰,并不能很好地表现出真实的瞬时频率轨迹。
2 深度脊波卷积自编码网络
AE是一种无监督神经网络,旨在将输入数据和输出数据的重建误差降至最低,标准AE包括输入层、隐层和输出层,激活函数是Sigmoid函数,标准AE的目的是最小化输入和输出之间的重构误差,以逼近一个恒等函数,从而自动完成特征提取,而脊波函数包含尺度因子、位移因子和方向因子,将脊波作为AE的激活函数具有更明显的优势。脊波自编码器(RAE)使用脊波函数代替AE的Sigmoid函数,具有比AE更优的特征提取和表示性能,RAE的结构如图6所示。
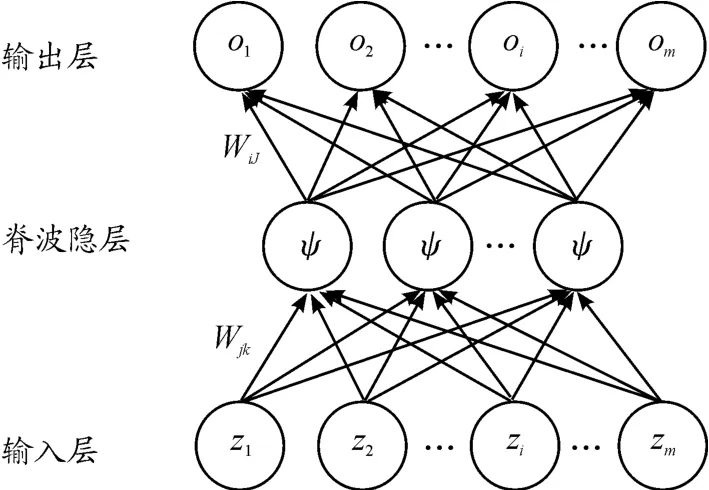
图6 RAE结构
图6 中m为RAE输入层和输出层神经元个数,Wij是输出层神经元i和隐层神经元j的连接权值,Wjk是输入层神经元k和隐层神经元j的连接权值。
一维卷积神经网络(1D-CNN)由一维卷积核和一维池化核构建。设c为当前层次,ic为该层输入,oc表示该层输出,wc和bc分别为该层连接权值和偏置,可得,则该层输出为:
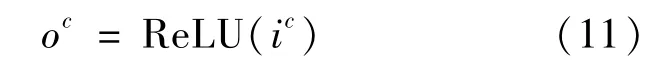
式中:ReLU为修正线性单元函数。对于卷积层,其前向传播公式为:
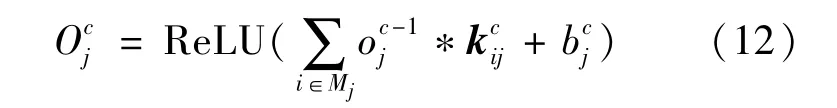
式中:j表示第j个特征映射图;Mj表示特征图集合,该特征图集合为第c层的第j个特征图和第c-1层相连接部分;表示该层卷积核权重向量;*为卷积符号。对于池化层,前向传播公式为:
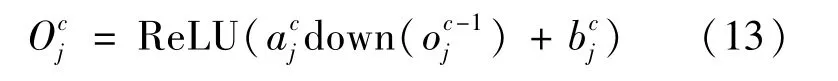
RAE得到的特征编码可以较好地重构原始数据,不易陷入局部最优,但RAE所需要调整的参数众多;而1D-CNN具有稀疏连接特性和权值共享特性,不易陷入局部最优。将RAE和1D-CNN相结合,可以构造出RCAE(脊波卷积自编码器)。对于输入信号x,RCAE第k个神经元的特征编码过程可以表示为:
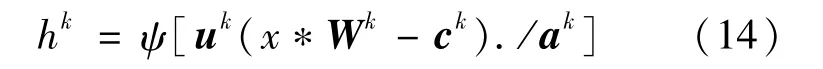
式中:ψ为小波函数;Wk为卷积核权重矩阵;ak、ck和uk分别为隐层脊波神经元的尺度因子、平移因子和方向因子向量;*为卷积符号;/为按元素相除符号,以Morlet小波的实部为例,有:
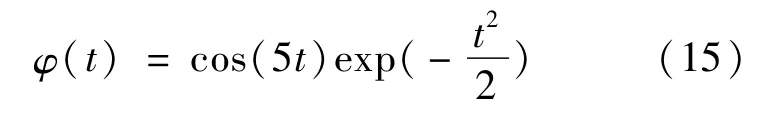
可将脊波神经元j的输出写为:
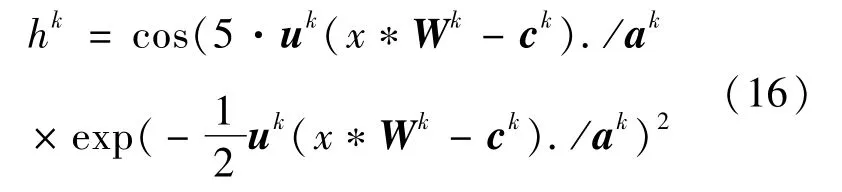
重构信号为:
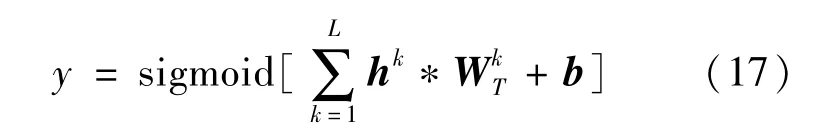
在RCAE基础上构建深度脊波卷积自编码网络(DRACN),堆叠多个RCAE进行逐层训练,将上一层RCAE的隐层输出作为下一级RCAE的输入,构成了多层次的网络结构。在DRCAN预训练过程中,所需的训练样本均为无标签样本,因此是无监督学习。无监督训练完成后,为进一步优化网络所提取的特征,在DRCAN最后一层加上Softmax层,使用带标签样本结合BP算法对网络整体微调,3隐层DRCAN结构如图7所示。
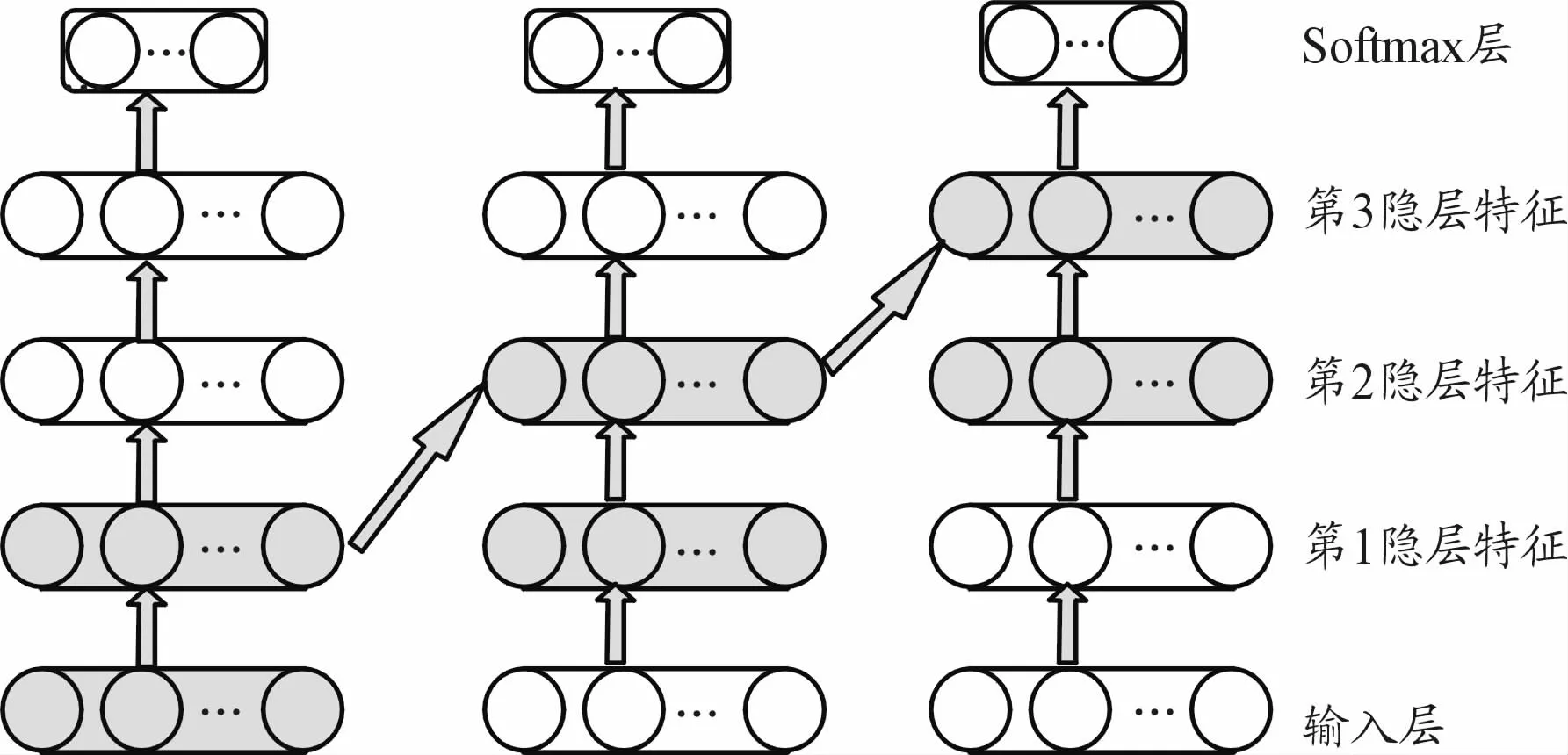
图7 3隐层DRCAN结构
网络的运行流程如下:首先,使用训练样本(无标签)训练第一个RCAE,并学习第1隐层特征(低层特征);随后,第1隐层特征成为第2个RCAE的输入,用于学习第2隐层特征(高层特征),而第2隐层特征将成为第3个RCAE的输入,以获得第3隐层特征(最高层特征);最后,将学习到的最高层特征输入到Softmax分类器中进行故障模式识别。
结合MSST算法,滚动轴承智能故障诊断方法的流程如图8所示。
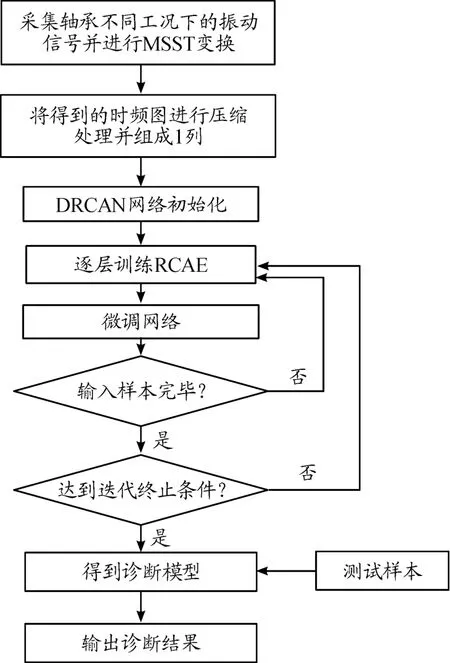
图8 诊断方法具体流程框图
首先,采集轴承不同工况下的信号并进行MSST变换,得到时频图像,随后,对时频图像进行降维处理构成样本集,根据数据量确定网络的深度以及各层神经元量等参数,进行逐层训练RCAE,并将测试样本输入最终得到的模型进行模型测试。
3 轴承故障诊断实例研究
3.1 实验装置及准备
为了验证多重同步挤压变换在实际情况下从原始信号中提取故障冲击特征以及深度脊波卷积自编码网络分类识别的能力,本文在实验室搭建试验台进行具体故障轴承的特征频率测试。实验平台如图9所示,其中包括速度传感器、转速传感器。实验模拟故障为使用电火花技术加工轴承的内圈、外圈以及滚动体上的断层。实验中采样频率为25.6 kHz,转速为1 800 r/min,负载735 W,转轴转1圈。采集了包含外圈故障、内圈故障以及滚动体故障等不同故障类形各1 000个样本。
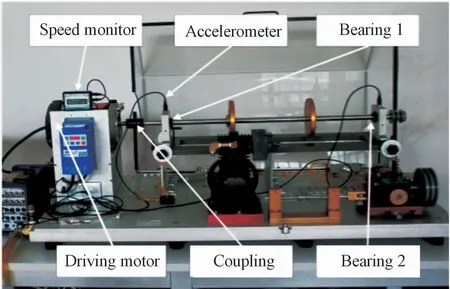
图9 实验平台
3.2 滚动轴承外圈故障诊断
滚动轴承外圈发生故障时,振动中由于外圈的位置一般都保持不变。因而故障部分所受的静载荷一般也保持不变。其故障信号频谱中主要包含转频、故障特征频率及其倍频等相关成分。取出上面实验所得外圈振动信号中的一个样本,实验室设定的外圈故障振动信号的转频29.89 Hz,故障频率87.5 Hz;该样本的外圈信号的时域波形图以及频谱图如图10所示。
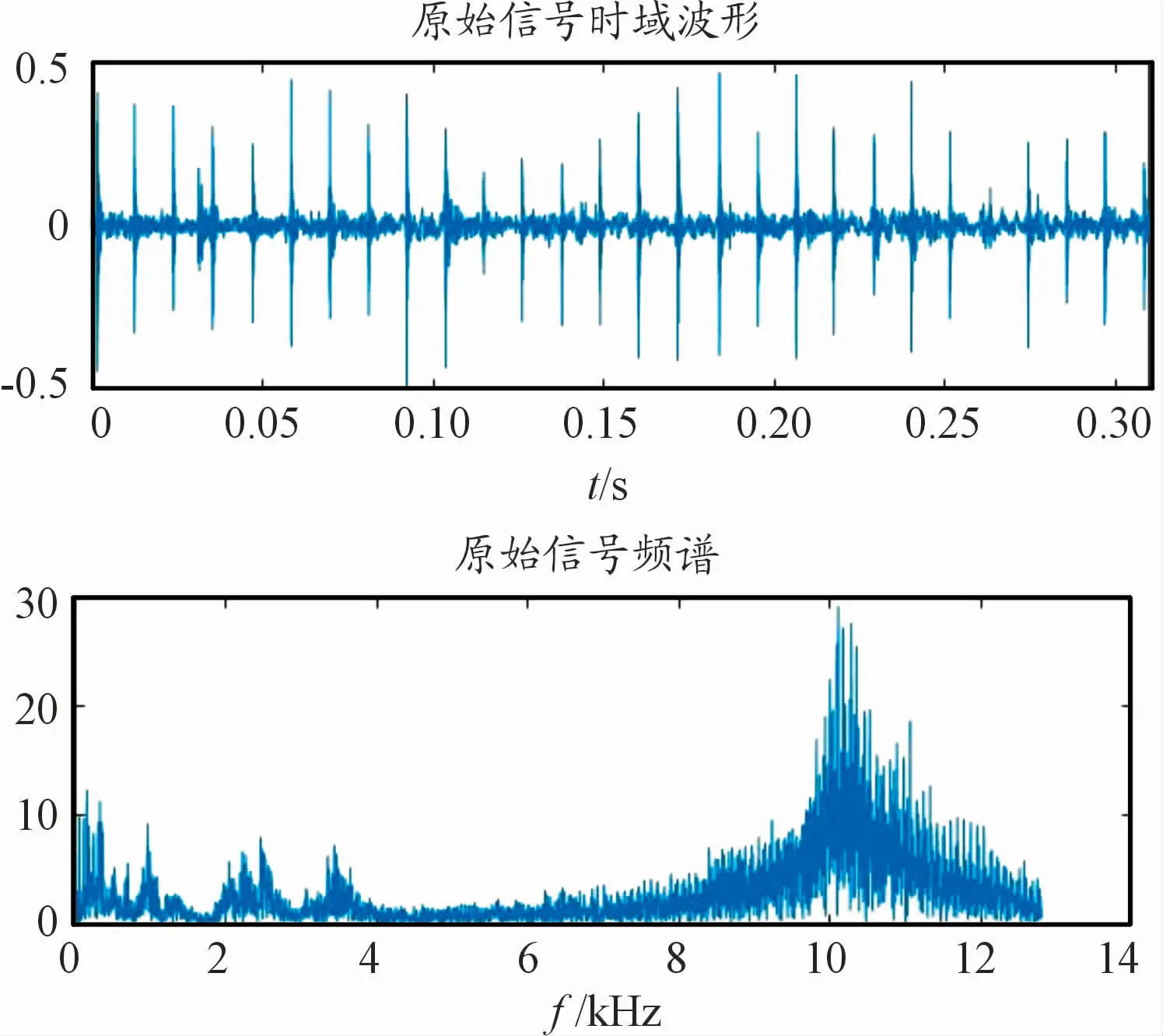
图10 外圈故障样本信号时频图
对图10所示信号进行分析处理,处理结果如图11~图13所示,MSST设定为进行6次SST。
针对图11~图13中处理结果,难以对比验证诊断的效果,需考虑算法的压缩效果,现对频率取对数进行时频分析,分析结果如图14所示。
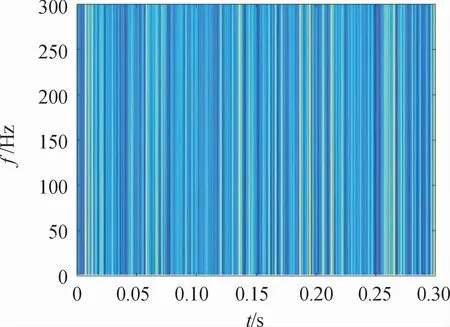
图11 样本信号STFT结果
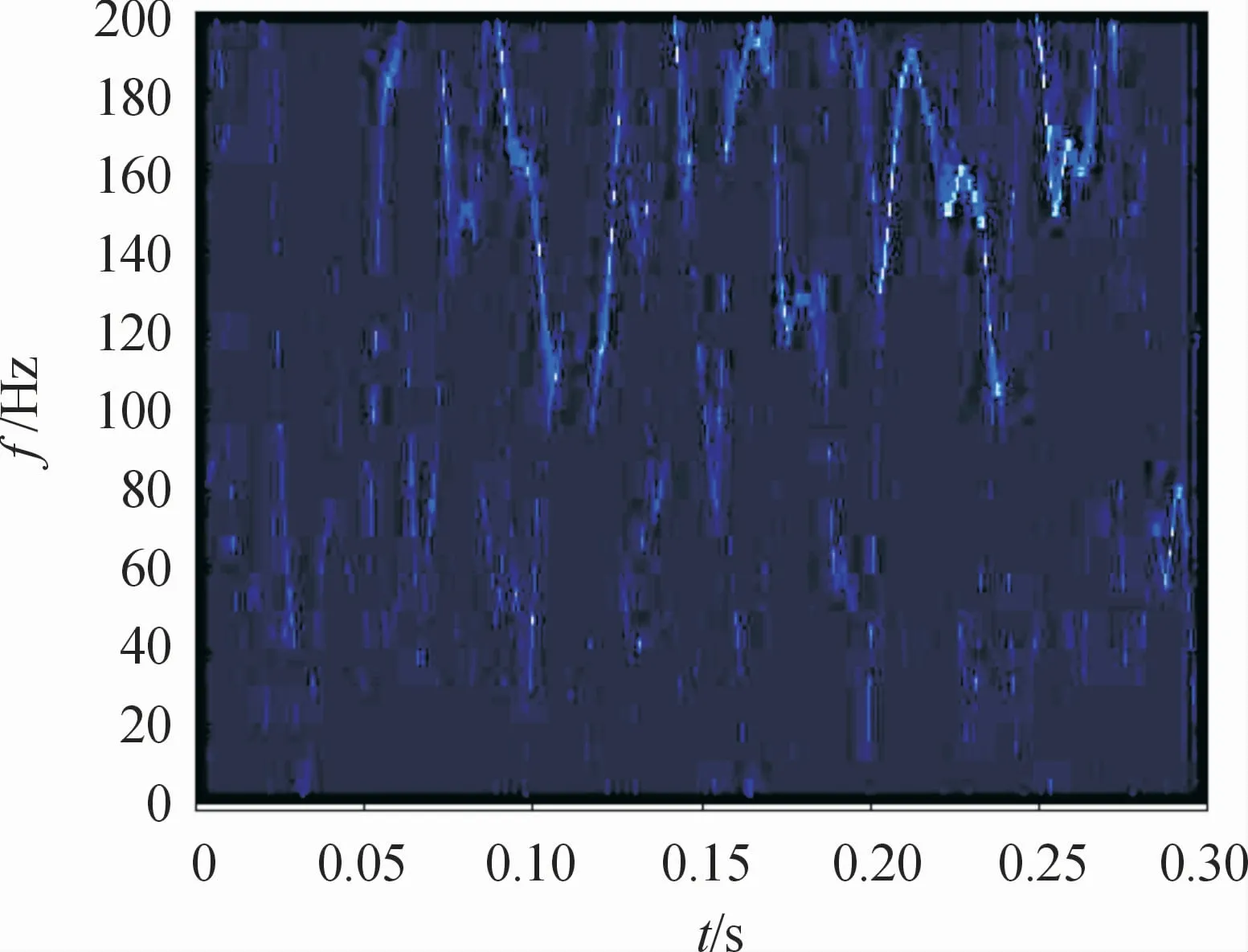
图12 样本信号SST结果
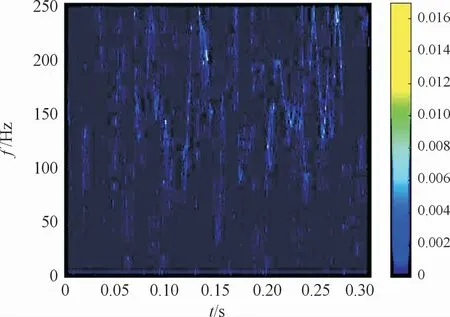
图13 样本信号MSST结果
图14 中按顺序依次分别为STFT、SST、二阶SST以及设定为8次SST的MSST处理结果。通过对比可较明显看出,MSST处理结果相比较其余3种方法所得的时频图像谱线更为清晰,对后续训练网络的特征识别帮助更大。
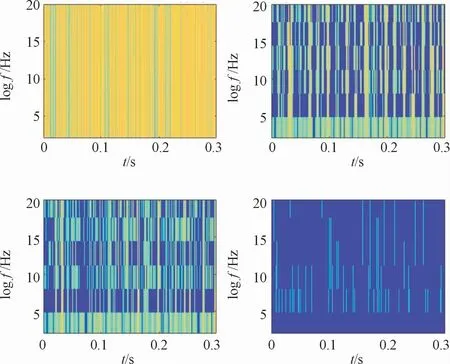
图14 频率取对数各方法处理结果
3.3 滚动轴承故障识别
实验中轴承内外圈以及滚动振动信号中均存在周期性冲击成分,故障信号受噪声干扰严重难以区分。使用MSST方法对此类故障信号进行预处理,随后,应用深度脊波卷积自编码网络对故障信号样本进行训练以及故障特征的分类识别,以探究2种方法结合应用的实际诊断效果。
前面共进行了4种工况实验,每种采集了1 000个信号样本,对采集得到各工况数据集中的信号进行MSST变换处理后,对时频图进行压缩至一定维度(30×30=900维)加入样本集。
随机选取样本集中的70%样本作为训练样本,剩下的样本作为测试样本。训练样本集中的训练样本集中随机选取80%样本作为无标签样本,用于预训练,20%样本作为带标签样本,用于微调。重复进行了5次实验以降低随机性,轴承工况类型分类如表1所示。工况1为轴承正常工作状况,工况2为外圈故障,工况3为内圈故障,工况4为滚动体故障。
在使用DRCAN进行训练时,为了对比研究该方法的处理效果,同样使用CNN(卷积神经网络)、DBN(深度置信网络)对实验样本进行对比训练分析,所选取实验信号中正常信号以及轴承3种故障信号的部分样本时域波形如图15所示,由上而下依次为轴承正常运转信号、内圈故障信号、外圈故障信号以及滚动体故障信号。
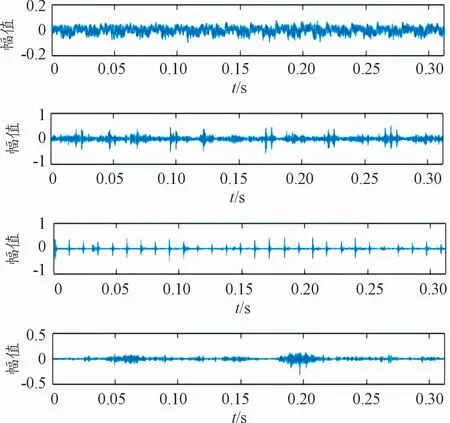
图15 部分样本时域波形图
实验测试中数据集情况如表1所示。

表1 实验测试中数据集
最终,各个方法中测试集的平均诊断识别正确率(%)如表2所示。
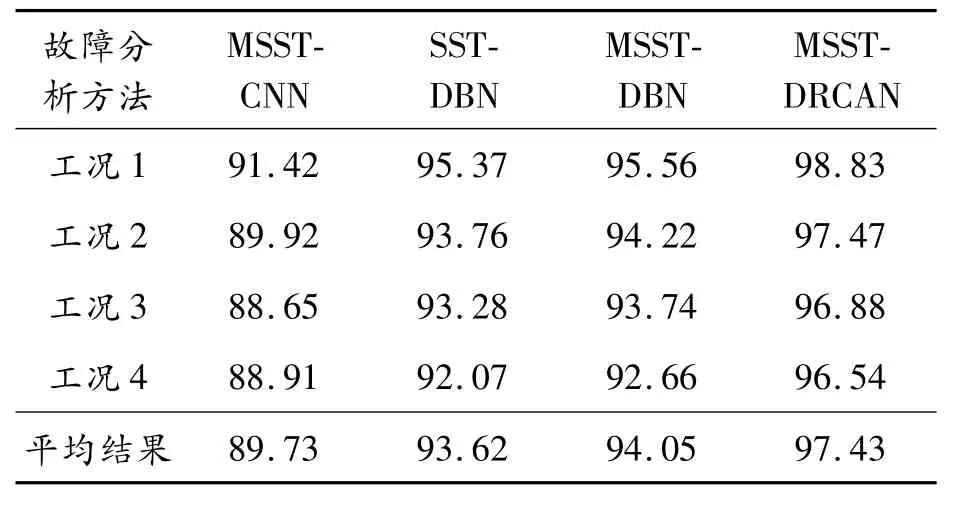
表2 平均诊断识别正确率 %
由表2可知,由于时频图分辨率更高的原因,在使用同一网络模型进行故障识别时,MSST的识别效果要优于SST。同时,相比较深度置信网络等模型,深度脊波卷积自编码网络具有更强的获取代表性故障信息的能力,能够有效识别不同的故障特征。
4 结论
本文提出了基于多重同步挤压变换(MSST)与深度脊波卷积自编码网络(DRCAN)的故障诊断方法,并将其应用于滚动轴承的故障诊断。实现了较为精确的轴承故障特证提取与分类,较其他诊断方法更具优势,主要结论如下:
1)MSST方法对滚动轴承故障信号进行预处理,结果具有较高的时频分辨率,有利于后续DRCAN网络的自动特征提取。
2)DRCAN将RAE与1D-CNN相结合,使得DRCAN网络学习到的特征,在尺度、位移和方向形变上具有特征不变性,增强了网络泛化性能,使得网络可以有效挖掘数据的本质特征。
3)在重构振动频段相接近的多分量信号时,MSST存在着交叉干扰等问题,实际诊断多故障类型时信号可能会出现该问题,需要进一步的研究与分析。
4)深度脊波卷积自编码网络的识别成功率较高,具有较好的自动提取特征能力,但网络训练耗时,需要进一步改进。
