基于BP神经网络学习算法的图像压缩技术研究

李亚文，何建强

（商洛学院电子信息与电气工程学院，陕西商洛 726000）

为了降低传输成本和提高传输速度，在图像进行传输之前，都要经过图像压缩去除冗余信息，图像压缩技术的关键就是尽量用少的数据量表示图像本身的信息。图像压缩算法较多，主要包括两类[1-2]：一类是冗余度压缩法，另一种是熵压缩，如：预测编码、变换编码等。哈夫曼提出构造编码的压缩方式，JPEG是一种基于差分预测编码的无损编码，DCT（离散余弦变换）和多种基于小波变换的图像压缩算法是有损编码，后来还有学者提出一种基于Haar小波变换的快速图像压缩算法[3]和基于字典模型压缩方法[4]等。人工神经网络模拟了人脑结构思维，其特色在于信息的分布式存储和并行协同处理，BP（Back Propagation）神经网络是人工神经网络中应用最广泛的一种，是1986年由RUMELHART和MCCELLAND为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，它的学习规则是使用最速下降法，通过反向传播不断调整网络的权值和阈值，使网络的误差平方和最小。本文将BP神经网络算法应用于图像压缩中，控制网络模型结构，进行分块运算，并进行了算法的实验仿真实现。

1 BP神经网络

BP网络可以解决那些无法用直观编程实现的事情，无法思考到其中的每一个步骤是怎样的机制，但是最终的数据可以直观得到，BP网络把学习和存贮的过程，大量地输入输出关系模式一一映射出来，不需要把映射关系提前揭晓。信号在传播的过程中，包括一个正向学习过程和一个误差反向学习过程，这个过程是反复进行的，不断循环形成一个网络训练学习过程，这就是BP神经网络算法的基本原理，正向传播是由输入层到隐层的一个过程，反向传播是输出层到隐层的一个误差反传过程[5]。

1.1 BP神经网络模型

BP算法的多层前馈网络可以看作是目前最广泛的神经网络，以较大的比率应用于生活中，当然单隐层网络更为普遍地应用于语言神经网络中。BP神经网络模型如图1所示，主要由输入层、隐层和输出层三部分组成[6]。

图1 三层BP网络模型

三层的网络中，输入向量X=(x1,x2,…,xi,…,xn)T，比如加入x0=-1，此时，可以为隐层引入阈值；隐层输出向量为Y=(y1,y2,…,yi,…,ym)T，如加入y0=-1可为输出层引入阈值；输出层输出向量为O=(o1,o2,…,ok,…,ol)T；期望输出向量为D=(d1,d2,…,dk,…,dl)T。输入层到隐层间的权值矩阵用V表示，V=(v1,v2,…,vj,…,vm)T，其中vj为隐层第J个神经元对应的权向量；隐层到输出层间，权值矩阵用W表示，W=(w1,w2,…,wk,…,wn)T，其中Wk为输出层第k个神经元对应的权向量[7]。

对于输出层有：

式(1)～式(6)共同构成了BP网络模型。

1.2 BP学习算法

构建BP网络模型后，实际的输出与期望输出的是完全一致，必定会存在一个网络误差E，改变误差可以通过调整权值实现，要使得权值调整与误差负梯度成正比例关系，那么有：

负号表示梯度下降，常数η∈(0，1)表示比例系数[9]，是学习速率的体现。

式(7)和式(8)是对数学表达权值思路做出的调整，并非是计算式的表达，在整个三层算法的推导过程中，对于输出层有j=1,2,…,m；k=1,2,…,l；对隐层有i=0,1,2,…,n；j=1,2,…,m。就输出层式(7)可以写成：

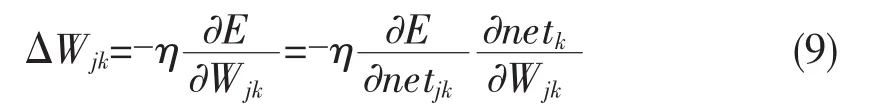
隐层，式(8)可写为：

输出层与隐层各定义一个误差信号，令：

因此，可改写权值调整式(9)为：

权值调整式(10)改写为[10]：

对于隐层，δyj可展开为：

对于输出层，可得：

对于隐层，可得：

因此，三层前馈网络的计算公式：

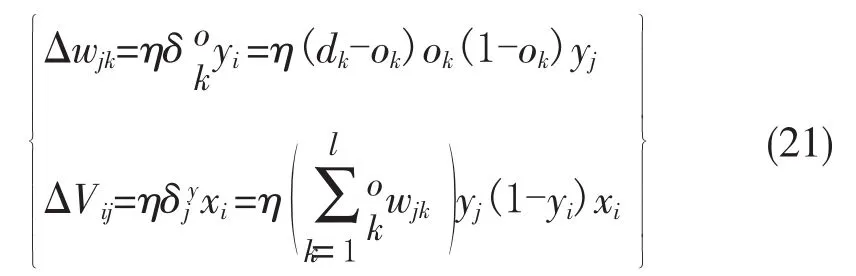
同时可以得出，BP算法学习过程中，各层权值调整公式大致一样。

2 BP神经网络进行图像压缩算法流程

BP神经网络中，输入层到隐层的映射关系通过编码器反应出，隐层直到输出层之间的映射关系，压缩比率（S）=输入层神经元个数/隐层神经元节点数。

BP神经网络应用图像编码的压缩比与输入层和隐层的节点数有关：

压缩比=输入层节点数（n）/隐层节点数（m）

网络设计主要包括：输入节点、层数、输出节点、每层激活函数、激活函数的确定、隐层节点数的确定。

1）输入/输出节点输入/输出节点是与样本直接相关的。本文用于压缩的原始图像均选为256×256的标准图像。

层数：为了获得好的压缩图像，使用不同的隐层层数来实现。

每层激活函数：隐层中一般采取S型的激活函数过程。

隐层节点数：网络训练精度的提高可以通过采用一个隐层。

2）初始参数的取值

输入输出数据的预处理：预处理采用的方法是归一化，把网络的输入输出数据限制在[0，1]或[-1，1]，BP网络其隐层使用Sigmoid函数。

BP网络是把误差反向传播算法对网络权值进行一定训练多层前馈网络的过程。其设计便是通过使网络输出和样本输出之间的网络权值误差之前平方和，具体算法实现流程如图2所示。

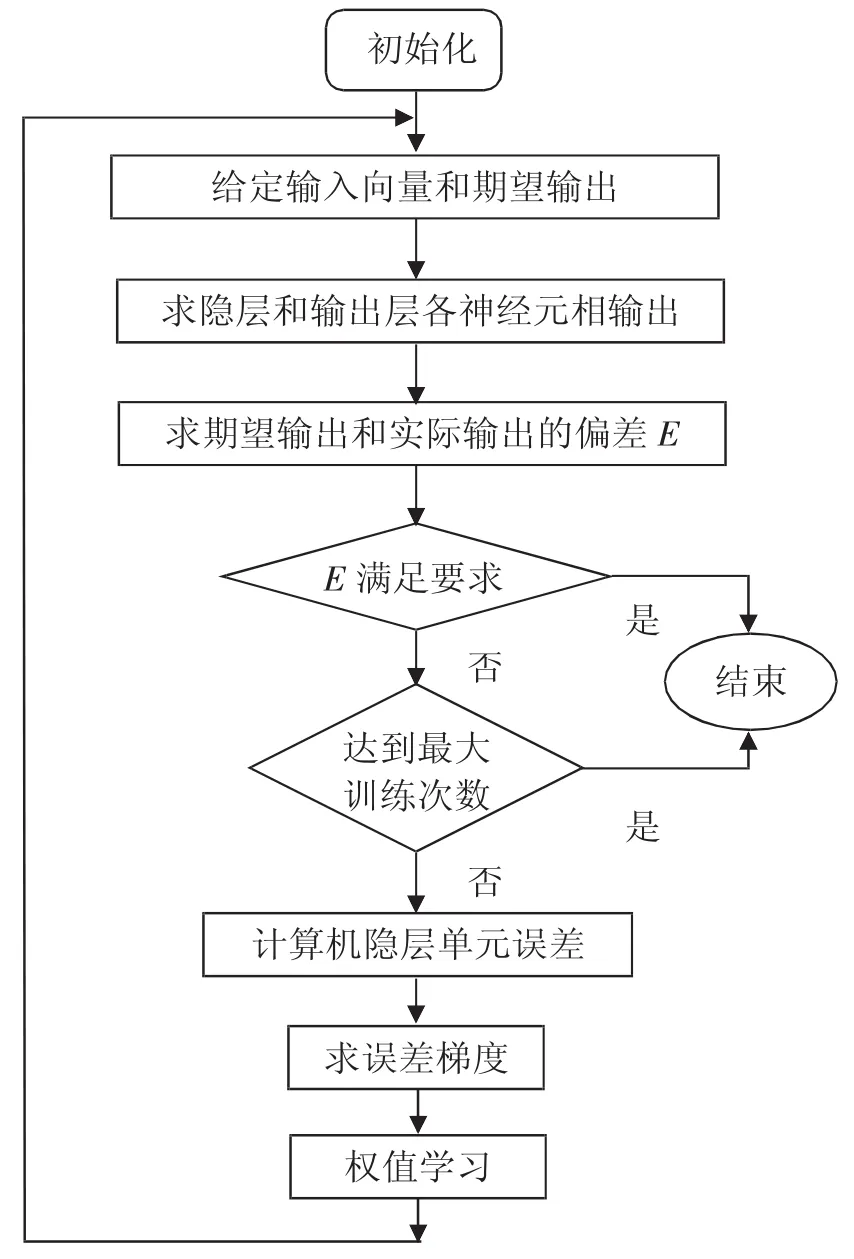
图2 BP算法实现流程图

3 BP神经网络学习算法进行图像压缩的实现

选取原始图像为Lena灰度图像如图3所示。为简单起见，设定网络的最大训练步数为500，目标误差0.001，选取的原始图像大小为256×256，图像压缩重建的质量将主要由隐层神经元个数N和子块大小K的不同来决定。

1）设定隐层神经元个数N为2，选取不同的K（子块大小）进行图像压缩。

以图3(a)原图为测试对象，分析当N=2时，不同子块K分别取2、4、8进行图像压缩，图像重建的变化情况如图3所示。当N=2时，不同子块大小K分别取2、4、8值时的检查功能图如图4所示。当N=2时，不同子块大小K分别取2、4、8值时的回归线图如图5所示。

图3 当N=2时，不同子块K压缩重建的图像

图4 当N=2时，不同子块的检查功能图

图5 当N=2时，不同子块的回归线

2）固定子块大小K=2作为标准，选取不同的隐含层神经元个数N值对比压缩重建图像效果。以图 3（a）原图为压缩对象，分别选N=1、2、4，压缩重建结果如图6所示。

图6 当子块K=2，不同隐层神经元个数N的压缩图像

图7是当子块K=2时，不同隐层神经元个数N=1、2、4时的检查功能图，在检查功能图中validation checks是防止网络训练过适。通常设置的检查默认值，随着网络的训练次数的增加，确认样本的误差曲线连续几次不再下降，这是训练终止的条件之一。图8是当子块K=2，不同隐层神经元个数N分别取1、2和4的回归线图，图9是当子块K=2，不同隐层神经元个数N的不同的指标参数指标图，图10是当子块K=2，不同隐层神经元个数N=1、2和4时PSNR（信噪比）参数表图。

图7 当子块K=2，不同隐层神经元个数N的检查功能

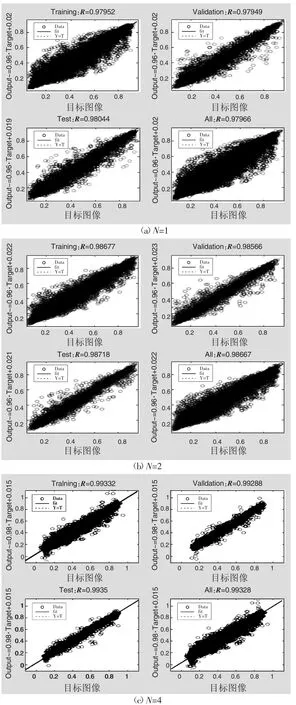
图8 当子块K=2，不同隐层神经元个数N的回归线

图9 当子块K=2，不同隐层神经元个数N的参数指标

图10 当子块K=2，不同隐层神经元个数N的PSNR参数

4 算法实现结果与分析

4.1 在确定N值时，变化K值

实验仿真中固定N=2，在不断增加k值，图像变得越来越模糊，图像所占的空间越来越少。T表示压缩所需时间长短，MSE表示图像之间的均方误差，PSNR体现峰值信噪比，Epochs体现训练步长。由图5可知，当N=2时，不同子块大小K分别取2，4，8值，可以明显观察到在K减小时，回归线越接近1，MSE表现出很好的训练效果。validation checks是防止网络训练过适。

由此得出，通过BP神经网络，图像压缩在K越小时，结果越好，均方误差使得它减少了，不过神经网络经过了很长的训练时间过程，只通过软件进行仿真，真实化很难实现。对网络训练时，限定目标误差为0.001。

4.2 在确定K值时，变化N值

分析图10可知，固定K=2，N不断增加时，峰值信噪比（snr）先增大后减小，压缩率（rate）逐步增，但是N不断增加时，训练时间变化与N没有直接的线性关系。可以总结出：本文算法中分块大小k越大，压缩质量越差，分块效应越明显。隐层规模增大时，图像不一定越清晰。神经网络的规模与图像压缩质量没有简单的线性关系。

5 结论

本文分析了BP神经网络学习算法的原理，在网络控制误差范围内进行网络分层训练，分别讨论了不同隐层神经网络层数N和分块数目K对图像压缩质量的影响等，为提高图像压缩质量与重建算法提供了重要的理论依据。下一步研究还可以将神经网络与其他压缩过程相联系，比如：神经网络实现预测编码过程、图像块的压缩编码等都可以通过BP神经网络学习算法实现。