基于RDPSO结构优化的三隐层BP神经网络水质预测模型及应用
2019-04-20
(云南省水文水资源局红河分局,云南红河661100)
水质预测是依据已有的历史监测数据,通过科学的方法推测将来的水质变化趋势,以期达到掌握水质现状及发展趋势的目的[1]。提高水质预测精度对于开展水环境质量评价、落实最严格水资源管理制度以及制订水污染控制系统规划等均具有十分重要的意义。由于水质受物理、化学和生物等水环境条件以及人类活动等众多确定性因素和随机因素的影响,致使传统回归分析等方法难以获得理想的预测效果。BP神经网络是人工神经网络应用最为广泛的神经网络模型之一,在各行业领域中,几乎90%以上的人工神经网络应用均是基于BP神经网络或改进型BP神经网络,其本身所具有的非线性映射能力和自适应、自组织、自学习等特性,已在水质预测中得到应用[2-4]。在实际应用中,由于单隐层BP神经网络初始权值阈值等参数通过随机确定,致使BP神经网络收敛速度慢、易陷入局部最优而不能获得较好的预测效果。目前,普遍采用遗传算法[5-6]、粒子群算法[7-8]等智能算法优化BP神经网络权值及阈值或增加BP神经网络隐层数来改善BP神经网络的预测性能。研究表明,同单隐层相比,多隐层BP神经网络泛化能力强,预测精度高,是提高BP神经网络预测性能的重要途径之一。目前已在径流预测[9]、水质预测[10]、风电功率预测[11]以及水安全评价[12]等方面得到应用,但多隐层BP神经网络的应用大部分仅限于双隐层。在水质预测实例研究中,文献[10]采用双隐层BP神经网络对老哈河化学需氧量(CODCr)、五日生化需氧量(BOD5)等指标进行预测,取得较好的预测效果;文献[3]采用三隐层BP神经网络对云南某水库总氮(TN)进行预测,并获得了一定的预测效果。但文献[3,10]不足之处在于采用人工试凑法确定网络结构,存在不能保证网络结构最优及人工试凑法繁琐等缺点。
基于上述原因分析,为有效提高水质预测精度,作者提出一种基于随机漂移粒子群(random drift particle swarm optimization,RDPSO)算法结构优化的三隐层BP神经网络预测方法,利用RDPSO算法优化三隐层BP神经网络隐层节点数,构建三隐层RDPSO-BP水质预测模型,并与基于单隐层、双隐层节点优化的RDPSO-BP神经网络、基于网络权值阈值优化的RDPSO-BP神经网络预测模型作对比,以云南省五里冲水库总氮预测为例进行实例研究,旨在验证三隐层RDPSO-BP模型用于水质预测的可行性和有效性。
1 三隐层RDPSO-BP预测模型
1.1 随机漂移粒子群算法
随机漂移粒子群(RDPSO)算法是孙俊等人受PSO算法的轨迹分析和金属导体中自由电子定向漂移运动、随机无规则热运动启发而提出来的一种具有较强全局搜索的群体智能算法。RDPSO算法中自由电子的定向漂移运动类似于粒子的局部搜索,随机无规则热运动类似于粒子的全局搜索[13]。参考文献[13-15],RDPSO算法数学描述如下。
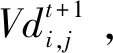
(1)
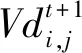
(2)


(3)

综上,RDPSO算法中粒子速度和位置更新公式表示为:
(4)
(5)

1.2 三隐层BP神经网络
BP神经网络是目前应用最广泛的神经网络模型之一,按结构可分为单隐层BP神经网络(三层网络)和多隐层BP神经网络(四层以上网络)。理论上,单隐层BP神经网络已能映射或逼近任何有理函数[16-17],但实际应用表明,对于复杂预测问题,单隐层BP神经网络往往表现出预测精度低和泛化能力弱等问题和不足;同单隐层BP神经网络相比,多隐层BP神经网络不但预测精度高、泛化能力强,而且易避免网络训练陷入局部最优。限于篇幅,多隐层BP神经网络拓扑结构及算法迭代步骤参见文献[9,18]。
研究表明,对于同一预测问题,多隐层BP神经网络的预测精度和泛化能力由隐层数和隐层节点数共同决定。对于相同隐层数的BP神经网络,隐层节点数之和越大,则网络拟合精度越高,但过多的隐层节点易导致网络“过拟合”而降低其预测精度和泛化能力;对于隐层节点数相同的BP神经网络,隐层数越多,则网络预测精度越高,但过多的隐层数不但增加网络的复杂程度,同时增加选择隐层节点数的难度。本文基于Matlab神经网络工具箱和三隐层newff()函数,利用RDPSO算法寻优各隐层节点数,以期获得三隐层RDPSO-BP模型理想的预测效果。
1.3 三隐层RDPSO-BP预测实现步骤
三隐层RDPSO-BP神经网络模型预测实现步骤可归纳如下(单隐层、双隐层RDPSO-BP神经网络模型可参如下步骤考实现;基本权阈值优化的RDPSO-BP神经网络模型可参考文献[6-8]实现)。
Step1合理划分训练样本和预测样本,利用式(6)对水质实测序列进行归一化处理。基于Matlab神经网络工具箱newff()函数构建三隐层BP神经网络,设定三隐层BP神经网络隐层节点数的搜寻范围。
(6)

Step2确定适应度函数。适应度函数是描述种群个体优劣程度的主要指标,本文选用训练样本均方误差作为适应度函数,描述如下:
(7)

Step3设置RDPSO算法群体大小N,最大迭代次数T,最大、最小热敏系数α、α′,常数c1和c2。设置当前迭代次数t=0,初始化粒子位置和速度。

Step5基于式(7)计算目标适应度值,更新全局最优位置G和粒子局部最优位置P。
Step6根据式(4)、(5)更新粒子的速度和位置。
Step7判断算法迭代终止条件是否满足,若满足则转至Step8,否则令t=t+1,并执行Step4—7。
Step8输出最优适应度值和最优粒子个体空间位置, 即三隐层BP神经网络各隐层节点数。
Step9利用RDPSO算法优化获得的各隐层节点数代入三隐层BP神经网络对预测样本进行预测。
2 实例应用
2.1 实例概况
五里冲水库位于蒙自市城东22 km期路白乡龙宝坡村,为红河州州府蒙自市城市主要供水水源。水库控制径流面积265.3 km2,多年平均径流量9 356万m3,总库容7 949万m3,兴利库容5 076万m3,设计年生活供水量2 190万m3,现状供水量1 516.8万m3,供水人口20.0万人。近年来,随着蒙自市人口的激增,径流区人类活动频繁、农业面源污染加剧,五里冲水库水质状况不容乐观。据云南省水环境监测中心红河分中心近5 a水质监测结果显示,五里冲水库2013—2017年年均水质评价均为Ⅲ类(依据GB 3838—2002《地表水环境质量标准》中规定的基本项目和补充项目评价,评价方法采用单因子评价法,监测频次为12次/a),主要影响因子为总氮,汛期由于降水冲刷等原因,总氮存在超标现象。
2.2 预测方法及对象
a) 预测方法。目前,总氮预测普遍采用2种方式:①利用同期监测相关性指标对总氮进行预测,但前提是总氮监测值与其他同期监测指标值具有较好的相关性;②利用总氮监测系列值,采用相空间重构法或自相关法确定影响向量(输入向量)对总氮进行预测。本文通过对五里冲水库水质监测结果进行分析,发现总氮监测值与其他同期监测指标值相关性较差,无法获得好的监测结果。因此,本文采用自相关法对总氮进行预测。
b) 预测对象。五里冲水库是蒙自市主要供水水源地,目前由云南省水环境监测中心红河分中心承担监测任务;监测项目为GB 3838—2002《地表水环境质量标准》中规定的基本项目和补充项目;监测频次为12次/a。本文收集五里冲水库2013—2017年60组总氮监测数据,利用SPSS软件对该总氮序列进行自相关分析,计算各阶自相关系数,见表1。
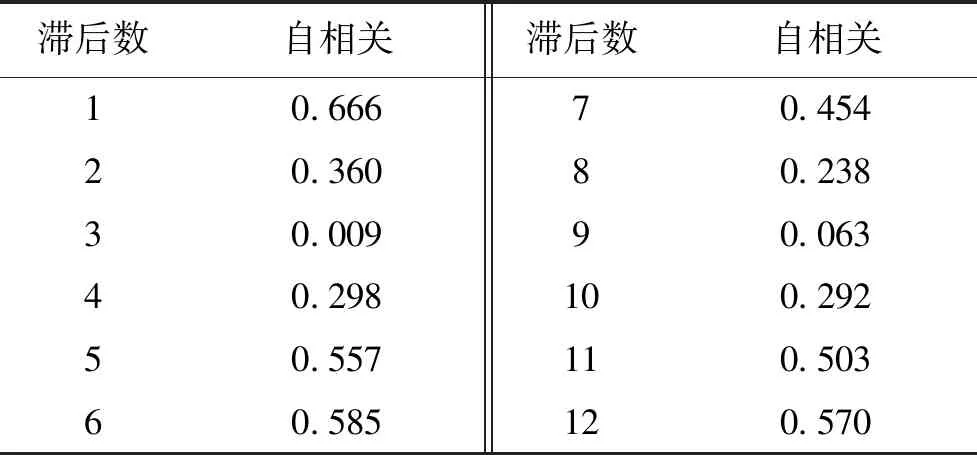
表1 总氮序列自相关系数
从表1来看,当滞后数(嵌入维数)为6时,自相关系数最大,为0.585。据此,构建嵌入维数为6维的输入向量和当月总氮序列为输出向量的三隐层RDPSO-BP神经网络总氮预测模型,60组监测数据共获得54组实验分析序列,并利用前50组总氮监测数据作为训练样本,后4组作为预测样本。限于篇幅,输入输出向量表从略。
2.3 预测结果
a) 参数设置。RDPSO算法最大迭代次数T=100,群体大小N=50,最大、最小热敏系数α、α′分别设置为0.9、0.3,常数c1、c2均设置为2。单隐层、双隐层、三隐层BP神经网络模型隐层传递函数采用logsig,输出层传递函数采用purelin,训练函数采用trainlm,学习速率lr为0.01,期望误差为0.008,最大训练轮回为100次,隐层节点数搜索范围∈[2,10]。RDPSO_BP神经网络模型权值和阈值搜索空间为[-1,1],隐层节点数为11,其他参数设置同上。
b) 模型构建及预测。基于上述分析,分别构建单隐层、双隐层、三隐层RDPSO_BP神经网络总氮预测模型,即构建RDPSO_BP_One、RDPSO_BP_Two、RDPSO_BP_Three预测模型,以及基于权、阈值优化的RDPSO_BP预测模型。选取平均相对误差绝对值MRE、最大相对误差绝对值MaxRE作为评价指标,利用此4种模型对五里冲水库总氮进行训练和预测,见表2(限于篇幅,仅给出预测样本相对误差)。并绘制训练~预测相对误差效果,见图1。

表2 五里冲水库总氮预测结果及其比较
注:表中加粗数字表示为最优值
3 结果分析
a) 从表2来看,无论是训练样本还是预测样本,三隐层RDPSO_BP神经网络模型的拟合-预测精度均优于单隐层、双隐层RDPSO_BP神经网络模型及基于权阈值优化的RDPSO_BP神经网络模型,其对于预测样本预测的平均相对误差绝对值为6.98%,精度分别比RDPSO_BP_One、RDPSO_BP_Two和RDPSO_BP模型提高了62.11%、42.07%和31.16%,具有较好的拟合、预测精度和泛化能力,表明RDPSO算法能有效优化三隐层BP神经网络的各隐层节点数,模型及方法可为水质预测及其他相关预测研究提供参考。

图1 五里冲水库总氮训练~预测相对误差效果
b) 从表2及图1来看,三隐层RDPSO_BP神经网络模型的总体拟合-预测平均相对误差绝对值达2.73%,拟合、预测效果明显优于其他3种模型,表现出较高的拟合-预测精度。可见,合理选择三隐层BP神经网络各隐层节点数能有效避免预测过程中“过拟合”和“欠拟合”现象的发生,进一步提高三隐层BP神经网络模型的预测精度和泛化能力。
c) 从表2预测结果来看,预测精度最高的是RDPSO_BP_Three模型,其次是RDPSO_BP和RDPSO_BP_Two模型,预测效果最差的是RDPSO_BP_One模型。RDPSO_BP和RDPSO_BP_Two模型预测精度在伯仲之间。可见,合理选取BP神经网络隐层节点数或优化BP神经网络权阈值,均能提高BP神经网络预测精度。
d) 从RDPSO_BP_One、RDPSO_BP_Two、RDPSO_BP_Three模型的拟合-预测结果来看,对于训练样本,单隐层、双隐层和三隐层RDPSO_BP模型的拟合精度分别为3.79%、2.95%和2.39%;对于预测样本,单隐层、双隐层和三隐层RDPSO_BP模型的预测精度分别为18.42%、12.05%和6.98%,从本预测实例来看,在相同条件下,BP神经网络拟合-预测精度以及泛化能力随着隐层数的增加而提高。
4 结论
a) 本文分析了单隐层BP神经网络模型在预测中存在的问题和不足,提出基于随机漂移粒子群(RDPSO)算法优化三隐层BP神经网络隐层节点数的预测方法,即通过RDPSO算法优化确定三隐层BP神经网络模型网络结构,并给出基于网络结构优化的三隐层BP神经网络模型构建方法和实现步骤,拓展了三隐层BP神经网络模型的应用范畴。
b) 本文构建三隐层RDPSO-BP神经网络预测模型,通过五里冲水库总氮预测实例进行验证,并与基于单隐层、双隐层节点优化的RDPSO-BP神经网络和基于网络权值、阈值优化的RDPSO-BP神经网络预测模型作对比。验证结果表明,在相同条件下,BP神经网络拟合-预测精度以及泛化能力随着隐层数的增加而提高。通过RDPSO算法优化确定三隐层BP神经网络各隐层节点数,可有效避免三隐层RDPSO-BP神经网络模型在预测过程中“过拟合”和“欠拟合”现象的发生,有效提高三隐层BP神经网络模型的预测精度和泛化能力。
c) 从实例预测结果来看,三隐层RDPSO-BP神经网络模型预测的平均对误差绝对值为6.98%,预测精度远高于其他3种模型,表明三隐层RDPSO-BP神经网络模型具有较高的拟合、预测精度和泛化能力,模型及方法可为相关水质预测研究提供参考。
