代价敏感正则化有限记忆多隐层在线序列极限学习机及图像识别应用
2018-06-01宋坤骏丁建明
宋坤骏,丁建明
(西南交通大学 牵引动力国家重点实验室,成都 610031)
如今,深度学习在图像识别领域[1-3]的正确率已经接近或超过人类,但深度学习算法的高额运行开销使得它在实用化方面还面临一些困难。例如,百度自主开发的Deep Image图像识别系统就需要运行在其自行研发的Minwa超级计算机上。为了在移动或嵌入式设备上更快更好地运行深度学习模型,需要在降低模型的开销上进一步努力。降低开销的思路是:(1)从根本上避免神经网络中用到的梯度下降等迭代步骤;(2)采用在线增量式训练算法代替离线批量式算法。将这两种思路结合,本文提出代价敏感正则化有限记忆多隐层在线序列极限学习机(CSR-FMML-OSELM)算法。
极限学习机(ELM)[4]是一种新型的单隐层前馈神经网络训练算法,近年来针对该算法进行了不少研究和拓展。Yang等人[5]提出了一种双端增量型极限学习机,这是一种通过网络余差反向传递的方式直接计算部分隐层神经元参数的算法,摆脱了隐层神经元完全随机选取的任意性对算法性能造成的不利影响。Cao等人[6]借鉴Learn++思想提出了一种基于投票机制的集成ELM算法,也属于一种ELM隐层参数选取随机性的解决思路。Liu等人[7]证明了有L个无限可微隐层节点的ELM网络的VC维数等于L。Yu和Deng[8]提出了将反向传播算法作用于网络的隐层参数上以压缩ELM网络的尺寸的思想,他们的方法将网络的模型尺寸压缩到了原先的1/16。张弦等人提出的限定记忆极端学习机(FM-ELM)是一种固定样本数量的在线序列极限学习算法,该算法每添加一个新训练样本的同时会丢弃一个距当前时刻最远的旧训练样本,以消除旧训练样本对于当前模型的不利影响[9]。
本文提出的CSR-FM-ML-OSELM算法相比张弦等人提出的算法,创新之处如下:(1)为了体现类别之间的不平衡性,在算法中加入了类别的权重因子,此即代价敏感性(CS);(2)将多隐层(ML)极限学习机[10]纳入在线学习的框架中;(3)为了进一步提升算法的性能,使用深度学习理论中常用的softplus激活函数代替ELM理论中的sigmoid激活函数;(4)为了提升稳定性和泛化性能,采用吉洪诺夫的正则化方法(R)。
1 代价敏感正则化有限记忆单隐层在线序列极限学习机
1.1 极限学习机简介
极限学习机其实是一种单隐层前馈神经网络的特殊训练算法,该算法最大特点在于极大地减少了需要迭代计算求解的权值和偏置个数,将原两层权值的迭代求解问题转换为通过最小二乘法求解最后一层的输出权值。因而不仅大大加快了训练速度,而且非但没有丧失泛化能力反而有所提升。设单隐层前馈网络的输出层和隐层神经元数分别为 m和L,则关于输入特征向量x∈Rd的第j维输出表达式为:

h(x)=[h1(x), h2(x), …, hL(x)]和 βj=[βj1, βj2, …, βjL]T依次是隐层激活函数向量和连接第j个输出层节点和各隐层节点的输出权值向量。非线性激活函数h(x)可以是 sigmoid,tanh,sin 等函数。ai=[ai1, ai2, …, aid]和bi则分别为连接输入层各节点和隐层第i个节点的输入权值及第i个隐层节点的偏置,输出权值矩阵βj=[β1, β2, …, βm]由式(2)经验风险最小化问题求出:

式(2)中的目标函数称为ELM算法的损失函数,容易看出,上述最优化问题可以用最小二乘法求解。Bartlett曾证明[13]:单隐层前馈神经网络的泛化能力与回归系数向量的范数大小呈负相关关系,因此满足权值最小的Moore-Penorse最小二乘解同时也是所有最小二乘解中泛化能力最好的,其回归系数向量(即输出层权重)的表达式为:

式(3)中,关于N个输入样本[x1, x2, …, xN]的隐层输出矩阵H定义为:

其中,L是隐层神经元数,N是输入样本数,而关于N个输入样本的训练数据目标矩阵则由式(5)定义:
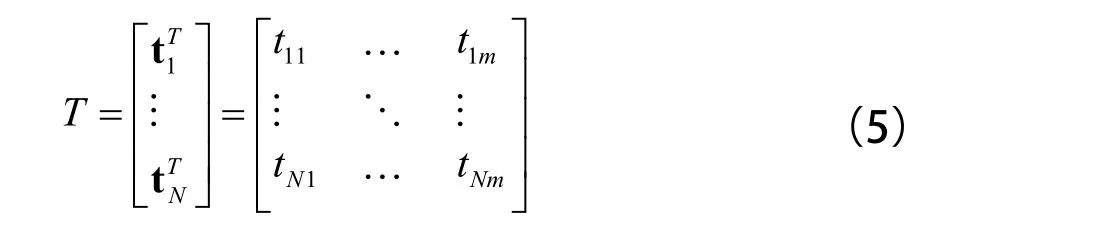
其中,m是输出维数。
广义逆矩阵H†的定义如下:当H†H为非奇异矩阵时,H†=(HTH)–1HT,而当 HHT为非奇异矩阵时,H†=HT(HHT)–1。由以上公式可以得出ELM算法的训练流程如图1所示。

图1 极限学习机训练流程
1.2 代价敏感正则化有限记忆单隐层在线序列极限学习机
为了体现不同类别故障误诊的代价差异性,对不同类别的样本引入不同的权重系数。假设第k类样本误诊的代价乘数是W(k),k=1, 2,…,Nc,这里,Nc是预先已知的类别总数,通常为了消除类别间数量上的不平衡,可以取W(k)=nk–1,即每一类样本数的倒数。下面用加权最小二乘法体现代价敏感性,而用增量式学习算法应对流式到来的故障数据。
加权最小二乘问题的表述是:设要求一组系数βj,使损失函数(Z–Hβ)取最小值,那么令偏导 αJ/∂β=–2HTWZ+2HTWHβ=0可以得到系数的加权最小二乘估计:β*=(HTWH)–1HTWZ。这里,H矩阵第i行第j列元素为第j个基函数hj(x)在第i个采样点xi的取值,W是各个权值组成的对角矩阵diag(W1, W2, …,WN),诸Wi从诸W(k)中取值,Z是输出目标值向量,xi=[x1i,x2i,…,xni]T是输入层向量(1≤i≤N) 。加权最小二乘法的损失函数为最小的充分条件是∂2J/∂β2=HTWH>0,即HTWH是正定矩阵。为了提高解的稳定性和泛化性能,通常在损失函数J中再加上一项正比于输出权值模平方的项1/2C(||β||2),对应于上述解中再增加一项正则化项I/C,得到:
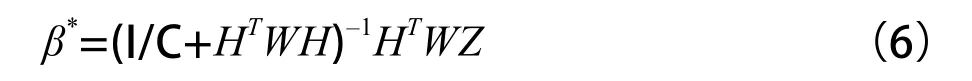
下面给出上述代价敏感正则化极限学习机的在线递推形式。每步递推可分成两个子步骤:(1)加入N1个新样本;(2)删去距当前时刻最远的N2个旧样本。有限记忆性由(2)体现。
假设新增的数据对应的矩阵块是ΔH(1),ΔW(1)和ΔZ(1),删除的数据对应的矩阵块是 ΔH(2),ΔW(2)和ΔZ(2),则由分块矩阵的运算知:

这里,角标(1)和(2)分别代表新增数据后和删除旧数据后的各个矩阵,由于

其中,K=(I/C+HTWH)。则由式(8)和式(9)以及Woodbury公式[11]经过简单推演可得如下输出层权值递推公式:


其中,P=K–1, P(1)=K(1)–1, P(2)=K(2)–1。每当有新数据到来时,据式(11)求解新增数据后的权值β(1),再据式(13)求解删除一定量旧数据后的权值β(2)作为反映最新数据的当前权值。
由公式的推导过程可见,每次有数据到来时新增数据量N1和删除的旧数据量N2不一定相等,两者间可以是任意的比例关系N2/N1,但需要在合理的范围内以保证任何时候都有N+N1–N2>0。
2 代价敏感正则化有限记忆多隐层在线序列极限学习机
作为多隐层在线序列极限学习机的基础,首先给出单隐层极限学习自编码器的训练流程:单隐层极限学习自编码器采用无监督的训练算法,无需给出训练类标签,其类标签就等于输入向量,除此之外,其训练算法同极限学习机的训练算法是类同的,均由式(6)给出,只是在式(6)中输出向量Z等于输入向量X,并且输入层的权值和偏置在随机选取后便按照Johnson-Lindenstrauss引理[12]予以正交化。
本节的多隐层在线序列极限学习机同上一小节中单隐层在线序列极限学习机之间的关系正如深度学习中堆栈自编码器同各层自动编码器(AE)之间的堆叠关系。多隐层的作用在于通过逐层递进的无监督学习自动提取特征。本节将沿用上节单隐层网络的递推算法给出多隐层网络的递推算法:在任何时刻t=k+1,用单隐层网络的递推公式求出第1隐层的输出层权值而后每一隐层的隐层输出矩阵可通过前一隐层的隐层输出矩阵用前向传播算法求出,其伪代码描述如下。
(1)初始化阶段
初始数据集{xi, ti}, xi∈d , ti∈m, i=1, 2,…, N0
For s=1 to p s为隐层数目
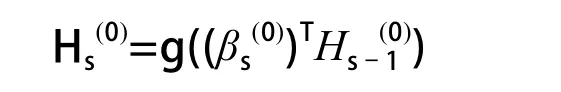
其中,由式(9)计算
End for
(2)在线学习阶段
For k=0 to tmax k为时间步数
For s=1 to p
H由式(1 3)计算
End for
3 实验研究
为了研究本文所提出算法的效果,分别在CIFAR-10物体图片库,MNIST手写数字库和ORL人脸库上进行对比实验。计算所用操作系统为Windows 7 64 bit旗舰版,CPU为Intel(R) Core(TM)i7-3520M@ 2.90 GHz,内存为8 GB,所用计算软件为Matlab R2016a。
CIFAR-10物体图片库包含60 000张像素为32×32的彩色照片,分成10类,每类中含有6 000张照片,共50 000张训练图片,10 000张测试图片。
图2给出了每类中10张示例图片。

图2 CIFAR-10示例图片
MNIST手写数字库中0-9每个数字有6 000张训练图片,1 000张测试图片,图片像素为28×28。
ORL人脸库包含40个人的共400张人脸照,每个人10张照片,每张像素为64×64。实验时每个人选择6张作为训练图片,4张作为测试图片。
实验时ELM网络的输入节点数取为图片的像素点数,对3类图片库分别为32×32,28×28和64×64;输出节点数取为已知类别总数,对3类图片库分别为10,10和40。3类数据库初始图片张数分别为15 000,15 000,200;每一时间步内进入的图片张数分别取为500,500,5。有限记忆性要求的每一时间步内删除的图片张数取为等于每一时间步内进入的图片张数。
图3~图5是在3组图片数据集上三隐层CSRFM-ML-OSELM和原始OSELM的测试集分类准确率随着其隐层单元数的变化关系图(三隐层是指中间隐层单元数),即3幅图中横轴是隐层神经元数,纵轴是测试集分类准确率。由图3~图5可见,不论是单隐层还是多隐层的极限学习机,测试集的识别准确率均有随着隐层神经元数增多而增多并渐趋饱和的趋势。根据这一趋势可以选择最优的隐层节点数以兼顾计算复杂度和分类准确率。由图4和图5可见,当隐层节点数较多时,本文提出的CSR-FM-MLOSELM算法对于手写数字辨识和人脸识别均达到了较好的准确率,最高都超过了95%,表明OSELM算法加入多隐层特性分类准确率有明显的提升。多层隐藏层确实能够学习到一些单隐层无法提取的高阶特征。

图3 CIFAR-10图片库2种算法分类准确率随隐层节点数变化
由于ELM隐层节点参数是随机选取的,所以为了避免分类准确率结果的不稳定性,在每组图片数据集上进行了10组实验,取各组实验识别率的平均值,记录下10组数据的标准差以跟踪2种算法的稳定性表现。2种ELM算法在3组图片数据集上的测试集准确率的标准差和平均训练时间如表1所示,其中,每组数据集左边一列是原始OSELM算法的数据,而右边一列是本文提出的CSR-FM-ML-OSELM算法的数据。
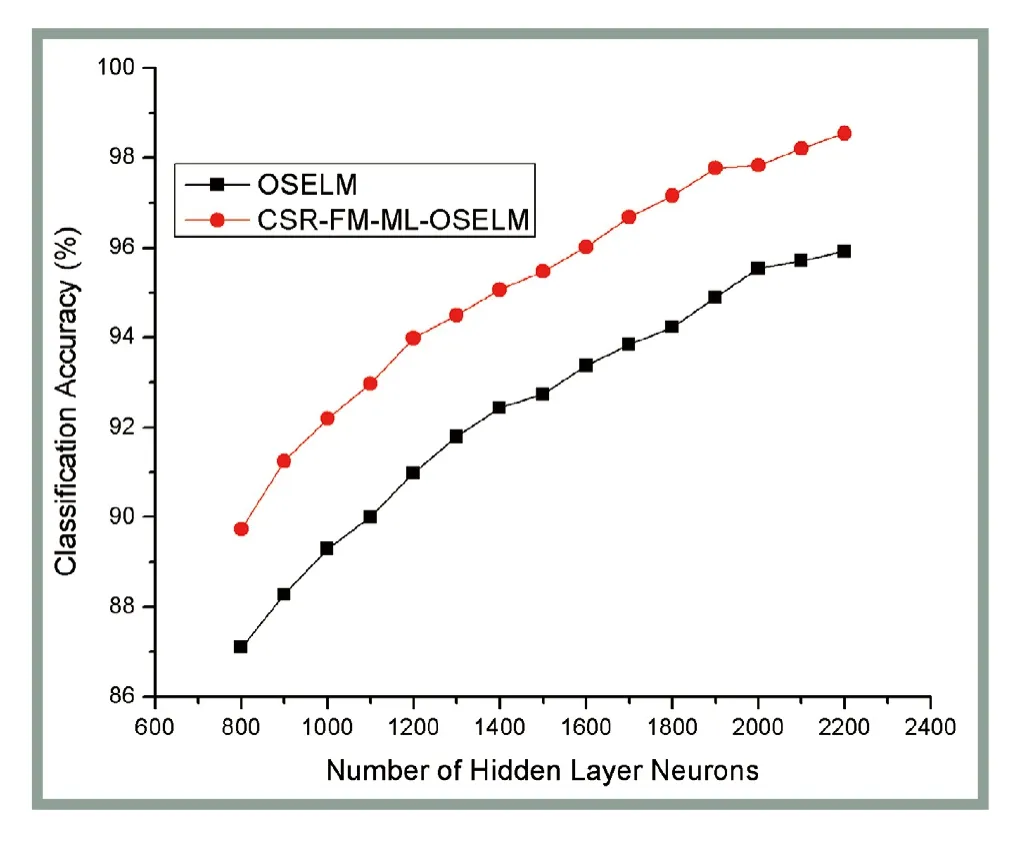
图4 MNIST图片库2种算法分类准确率随隐层节点数变化
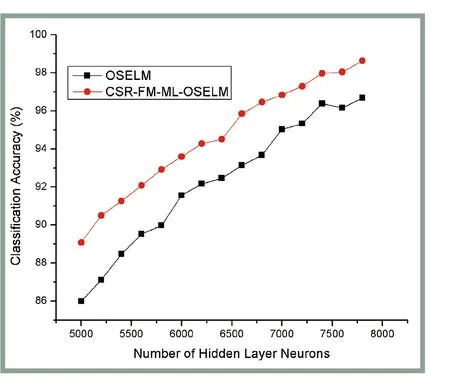
图5 ORL人脸库2种算法分类准确率随隐层节点数变化
由表1可见,在由测试集准确率标准差体现的算法稳定性方面,本文提出的CSR-FM-ML-OSELM算法胜过原始的OSELM算法。同时,本文算法的训练时间显著低于现有的深度学习算法,且多隐层特性加入在线序列极限学习机后,相比单隐层的在线序列极限学习机而言,训练时间提升幅度并不大。

表1 本文算法和原始OSELM算法在3组图片库数据集上测试集准确率标准差和平均训练时间
表2 所示为在不同的正则化参数C和权重W(k)取值下CSR-FM-ML-OSELM和CSR- OSELM人脸识别的平均准确率。表2中,每个C值下的左右两列分别代表权重W(k)=nk–1和W(k)=1两种情况,其中,W(k)=1,C=1030的CSR-OSELM算法就相当于原始的OSELM算法。从中可看出,原始OSELM算法的测试集准确率91.9%要显著低于最高的准确率97.5%,带有多隐层和有限记忆性质的CSR-FM-MLOSELM算法的准确率要高于同样参数的不带这些性质的CSR-OSELM算法的准确率,并且随着参数C的增加,也即正则化项作用的减弱,准确率有下降趋势。同时,左列带了加权处理情形的准确率要高于右列不带加权情形的。说明多隐层、有限记忆性、正则化和代价敏感性这些性质对于提升泛化性能都是有一定作用的。
4 结束语
本文将代价敏感性(CS)、有限记忆性(FM)和多隐层特性(ML)添加到了在线序列极限学习算法中,提出代价敏感正则化有限记忆多隐层在线序列极限学习机(CSR-FM-ML-OSELM)算法。实验结果表明,多隐层特性有效地模仿了深度神经网络的特点,提升了图像识别的准确率,在MNIST手写数字库和OCL人脸库上取得了同深度学习可比的结果,并且模型的训练速度大大快于深度神经网络。同时,在线多隐层极限学习算法除了在泛化性能上较在线单隐层极限学习算法有较大提升外,在泛化性能的稳定性上也有所改善。
[1]He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[C]// Computer Vision and Pattern Recognition.IEEE, 2016:770-778.

表2 CSR-FM-ML-OSELM和CSR-OSELM算法的平均人脸测试集准确率
[2]Panda P, Sengupta A, Roy K. Energy-Efficient and Improved Image Recognition with Conditional Deep Learning[J]. Acm Journal on Emerging Technologies in Computing Systems,2017, 13(3):1-21.
[3]Miyazono T, Saitoh T. FishSpecies Recognition Based on CNN Using Annotated Image[C]// International Conference on Information Theoretic Security. Springer, Singapore, 2017:156-163.
[4]Huang, G.B., Zhu, Q Y., Siew, C.K. Extreme learning machine:theory and Applications[J]. Neurocomputing, 2006, 70(1):489–501.
[5]Yang Y, Wang Y, Yuan X. Bidirectional Extreme Learning Machine for Regression Problem and Its Learning Effectiveness[J]. IEEE Transactions on Neural Networks &Learning Systems, 2012, 23(9):1498-1505.
[6]Cao J, Lin Z, Huang G B, et al. Voting based extreme learning machine[J]. Information Sciences, 2012, 185(1): 66-77.
[7]Liu X, Gao C, Li P. A comparative analysis of support vector machines and extreme learning machines [J]. Neural Networks,2012, 33(9): 58.
[8]Yu, D., Deng, L. Efficient and effective algorithms for training single hidden-layer neural networks [J]. Pattern Recognition Letters,2012, 33(5): 554–558
[9]张 弦,王宏力. 限定记忆极端学习机及其应用[J]. 控制与决策,2012,27(8):1206-1210.
[10]Tang J, Deng C, Huang G B. Extreme Learning Machine for Multilayer Perceptron[J]. IEEE Transactions on Neural Networks & Learning Systems, 2017, 27(4):809-821.
[11]Deng C Y. A generalization of the Sherman–Morrison–Woodbury formula[J]. Applied Mathematics Letters, 2011,24(9):1561-1564.
[12]Blocki J, Blum A, Datta A, et al. The Johnson-Lindenstrauss Transform Itself Preserves Differential Privacy[C]// IEEE,Symposium on Foundations of Computer Science. IEEE Computer Society, 2012:410-419.
[13]Bartlett P. The sample complexity of pattern classification with neural networks: the size of theweights is more important than the size of the network [J]. IEEE Transactions on InformationTheory. 1998, 44 (2): 525–536.
