T型裂纹梁的自振特性分析
2021-05-17韩慧璇张建东胡朝斌
张 姗,周 叮,韩慧璇,张建东,胡朝斌
(1. 南京工业大学 土木工程学院,南京 211816;2. 江苏科技大学 土木工程与建筑学院,镇江 212000)
工程实际中,结构长期承受不规则荷载作用,导致梁式构件带裂纹工作。裂纹的存在成为结构安全的一大隐患,裂纹会导致结构刚度的降低,不仅会影响结构的动力学特性,甚至可能导致结构整体性破坏(如梁板开裂、桥面断裂等)。T型梁作为实际工程一种常见的结构,分析裂纹对其动力学特性的影响,对结构的安全性具有重要意义。
国内外一些学者对裂纹梁的损伤展开了研究。Chondros等[1]基于一维裂纹梁理论,提出一种求解裂纹梁动力特性的双线性方法,对含呼吸裂纹简支梁的横向振动进行了分析。Chondros等[2]进一步基于断裂力学理论,将裂纹影响等效为连续变化的梁柔度,提出了一种求解裂纹梁振动的方法。Kim等[3]利用弹簧模拟梁的任意边界条件,用柔度系数的逆表示裂纹处的连续刚度。吴宁祥等[4]建立集中柔度模型,利用无质量弹性铰模拟裂纹引起的局部柔度变化,分析了Eluer梁的裂纹无效位置点。张炜等[5]采用无质量扭转弹簧,结合递推法求解了各种边界条件下含任意条裂纹的梁的振动特性。Ricci等[6]使用线弹簧代替裂纹,利用裂纹尖端奇异应力分布计算裂纹的强度因子,采用动刚度矩阵法研究了含裂纹T型梁的弯扭耦合振动。Zeng等[7]利用有限元法,对含不同类型裂纹的悬臂梁进行了动力特性分析。马辉等[8]进一步基于有限元法,分析了含斜裂纹悬臂梁的非线性振动特性。蒋杰等[9-10]基于能量法,利用Ritz法研究了端部含裂纹悬臂梁的振动特性。杨鄂川等[11]基于等效刚度法建立裂纹梁分析模型,用求解变截面梁振动的半解析法分析了含裂纹Timoshenko梁的振动特性。Lee等[12]采用边界元法求解了裂纹梁的固有频率,利用牛顿迭代法分析了裂纹位置、裂纹深度的影响。Zhang等[13]采用修正傅里叶级数法对含多个横向裂纹的Timoshenko梁进行了研究,将求解裂纹梁的固有频率转化为一标准的线性特征方程问题。上述研究大多是基于Euler梁理论或Timoshenko梁理论对矩形截面梁进行分析,尚未见有对含裂纹的T型截面梁进行研究。
为获取精确的动力学解,本文基于弹性力学理论分析T型梁的自振特性。利用转化截面法,将T型梁等效为具有不同材料性能的两层矩形截面梁,并将等效后的裂纹矩形梁划分为四个子域,通过Chebyshev-Ritz[14]法分别求得各子域的特征方程,再由各子域层间交界处的位移连续条件得到等效后的T型裂纹梁的总体特征方程。
1 T型裂纹梁模型
1.1 简化T型梁模型
如图1所示,利用转换截面法,根据应变相同且总内力不变原则,将T型梁翼缘折算成与腹板宽度一致的矩形截面。即等效前后翼缘的拉压刚度EA和弯曲刚度EI均保持不变,翼缘等效前后弹性模量关系满足
(1)
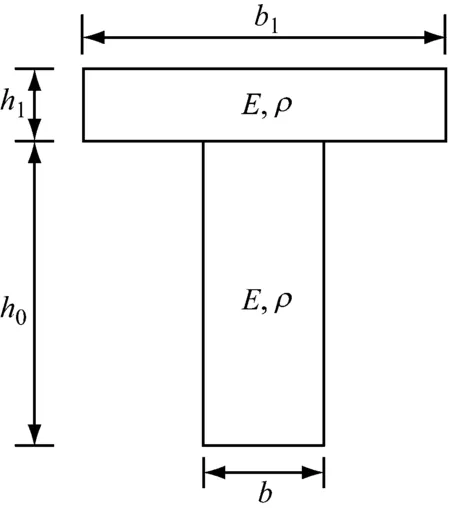
(1) 原截面
式中:E为等效前T型梁的弹性模量;E1为翼缘等效后的弹性模量;b、b1分别为腹板和翼缘的宽度。
在对结构进行动力学分析时,考虑惯性力的因素,需对T型梁翼缘的材料密度也进行等效,保证等效前后翼缘质量不变,即:
(2)
式中:ρ为等效前T型梁的材料密度;ρ1为等效后T型梁翼缘的材料密度。
1.2 T型裂纹梁的分析模型
考虑开口型裂纹,即在荷载作用下梁底部的裂纹不闭合。等效的T型裂纹梁被离散为四个子域,如图2所示。建立直角坐标系,分别对每段子域进行独立分析。假设含单裂纹T型梁长l,高h,腹板宽b,T型梁翼缘厚度为h1,宽为b1,梁底端l3处有一开口裂纹,深度为h3,梁腹板上表面至裂纹尖端距离为h2。梁的材料属性分别为:泊松比为μ,子域q(q=1,2,3,4)的弹性模量为Eq,子域q的材料密度为ρq。

图2 含单裂纹T型梁子域模型Fig.2 T-beam sub-domains model with single crack
2 子域分析
2.1 子域能量表达式
基于精确的二维弹性力学理论,对于平面应力问题,子域q的应力-应变关系满足
(3)
相应地,由几何方程,子域q的应变-位移关系满足
(4)

各子域的应变能Vq、动能Tq可表示为
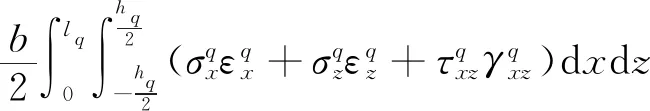
(5)
(6)
式中:t为时间;lq和hq分别为子域q的长度与高度。
2.2 子域自由振动方程
为简化计算,对笛卡尔坐标进行无量纲化处理,即令:
(7)
根据分离变量法,子域q的自由振动位移方程可表达为振型函数与时间函数乘积的形式,即:
uq(x,z,t)=Uq(ξq,ζq)ejωt,
wq(x,z,t)=Wq(ξq,ζq)ejωt
(8)
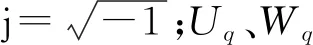
将式(8)代入式(5)、(6)中,可分别得到子域q的最大弹性应变能Vmax,q和最大动能Tmax,q,分别为:

(9)
(10)
式中,λq=hq/lq。
在Ritz法中,构造Uq、Vq合适的试函数是非常重要的,不同形式的试函数,其准确性和收敛性是不同的。Chebyshev多项式的正交完备性可保证构造的试函数获得高收敛性的Ritz解[9-10],故本文将各子域的试函数表示为几何边界特征函数与第一类Chebyshev多项式乘积的形式,利用边界特征函数分量来满足边界约束条件。即子域q的位移函数可表示为
Uq(ξq,ζq)=
Wq(ξq,ζq)=
(11)
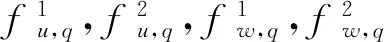
Ps(χ)=cos[(s-1)arccos(χ)]
(s=1,2,3…)
(12)
为确保位移函数式(8)满足结构的几何边界条件,需寻找相应的边界特征函数。表1给出了几种经典边界条件下边界特征函数分量的表达式。
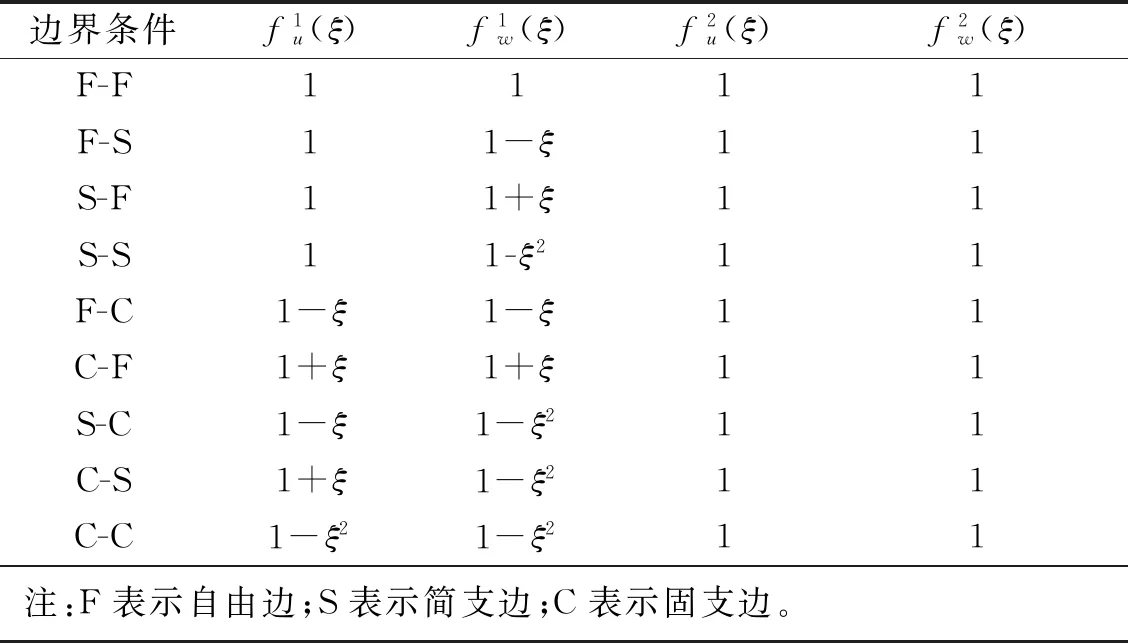
表1 经典边界条件下边界特征函数分量Tab.1 The characteristic boundary function components of various classical boundary conditions
2.3 子域振动特征方程
利用Ritz法建立子域q的振动特征方程。由最小势能原理,满足位移边界条件的各种状态中,真实位移需使结构的总势能取极小值。因此,对未知系数Aij,q、Bmn,q求极值,导出子域q的振动特征方程。
子域q的能量泛函Πq为
Πq=Vmax,q-Tmax,q
(13)
要求最小泛函有
(14)
将式(9)、(10)代入式(13)、(14)中,得子域q的振动特征方程
([Kq]-Ω2[Mq]){Xq}=0
(15)
式中:Ω为无量纲固有频率;[Kq]和[Mq]分别为子域q的刚度矩阵和质量矩阵;{Xq}为Aij,q、Bmn,q构成的列向量。式(15)中
(16)
(17)
(18)
(19)
{Aq}=
{A11,qA12,q…A21,qA22,q…Ai1,q…Aij,q}T
(20)
{Bq}=
{B11,qB12,q…B21,qB22,q…Bi1,q…Bij,q}T
(21)
矩阵元素为
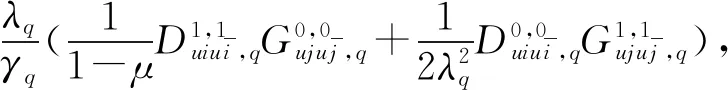
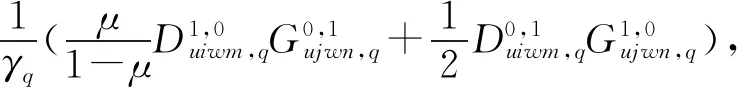

(22)
其中,
γq=hqlq/hl
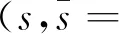
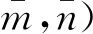
(23)
3 T型裂纹梁的自振特征方程
将各子域刚度矩阵、质量矩阵进行总合得到整个梁的振动特征方程,其表达式为
([K]-Ω2[M]){X}=0
(24)
其中,
(25)
(26)
(27)
由切比雪夫多项式性质,可知:
Pn(1)=1,Pn(-1)=(-1)n-1
(28)
(29)
考虑相邻子域界面处的位移相等,故子域1与子域2,子域2与子域3、4在界面上有如下关系式
U1(ξ1,-1)=U2(ξ2,1),W1(ξ1,-1)=W2(ξ2,1),
U2(ξ2,-1)=U3(ξ3,1),W2(ξ2,-1)=W3(ξ3,1),
U2(ξ2,-1)=U4(ξ4,1),U2(ξ2,-1)=U4(ξ4,1),
ξ2=ξ1,-1≤ξ1≤1
(30)
将位移函数式(11)代入式(30),作切比雪夫多项式展开,得到:
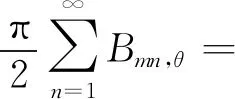
(31)
其中,
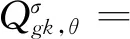
(32)
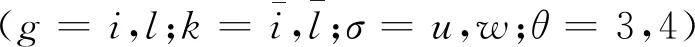
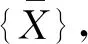

(33)
将式(33)代入式(24),消去因位移连续性导致的未知系数线性组合后,T型裂纹梁特征方程转化为
(34)
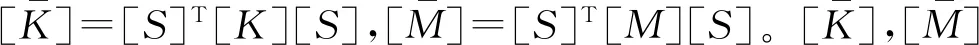
4 算例分析
对两端固支含裂纹T型梁的振动特性进行分析。梁材料性能参数取值为:弹性模量E=210 GPa,材料密度ρ=7 800 kg/m3,泊松比μ=0.3,翼缘宽度与梁高b1=h=0.5 m,腹板宽b=0.25 m,翼缘厚度与梁高比h1/h=0.2。
4.1 收敛性分析
考虑裂纹深度为h3/h=0.2,裂纹位于跨中(l3/l=0.5),研究不同高跨比(h/l=0.1、0.25、0.5)和不同级数项下T型裂纹梁前8阶无量纲频率参数Ω的收敛性。为简便起见,各子域位移函数Uq,Wq(q=1,2,3,4)选取相同数量的级数项,计算结果如表2所示。

表2 不同级数项下两端固支T型梁无量纲频率参数Ω的收敛性Tab.2 Convergence of non-dimensional frequency parameters Ω of fixed at two ends T-beam in term of different series terms
由表2可见,结构无量纲频率参数随着级数项的增加而减小,级数项在坐标x方向对频率参数的影响远大于z方向上的级数项,这说明梁在厚度方向的级数项对结构频率参数的影响相对较小。当项数级达到50×10时,频率参数的精度可达到三位有效位数。
从表2可以看出,随着结构高跨比的增大,梁各阶无量纲频率参数随之增加。
4.2 有限元解比较
为验证本文方法的正确性,将本文解与等效前后两模型的有限元ANSYS解进行比较。等效前原裂纹梁选用8节点SOLID185单元进行模拟,共计97 890个单元;等效后的裂纹梁选用PLANE183单元进行模拟,划分为6 250个单元。对比分析高跨比为h/l=0.1,裂纹位于跨中(l3/l=0.5),不同裂纹深度(h3/h=0.2、0.4、0.6、0.8)下,裂纹梁的前3阶无量纲频率参数值,如表3所示。从表3可知,本文解与有限元解之间的相对误差具有良好的吻合性,与等效前比,最大误差为5.64%(0.165 5对0.175 4);与等效后比,最大误差仅为0.71%(0.493 1对0.496 6),证明转换截面模型保持了较好的准确性。

表3 固支裂纹梁本文解与等效前后有限元解的对比 (h/l=0.1,l3/l=0.5)Tab.3 Comparison of present solutions and FE solutions equivalent for fixed cracked beam
4.3 裂纹深度及裂纹位置对振动模态的影响
4.3.1 裂纹深度及裂纹位置对固有频率的影响
计算高跨比为0.1的T型裂纹梁在不同裂纹参数下的无量纲频率,分析裂纹参数对固有频率的影响。
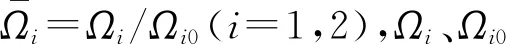
从图3可知,裂纹梁固有频率随裂纹深度的增加而下降。当裂纹位于跨中(l3/l=0.5)时,一阶固有频率随裂纹深度增加下降明显,二阶固有频率随裂纹深度变化较小;当裂纹位于0.2l及0.8l时,裂纹对一阶固有频率的影响较小;裂纹位于0.3l及0.7l时,二阶固有频率随裂纹深度增加下降明显。
4.3.2 裂纹深度及裂纹位置对振型的影响
计算高跨比为0.1时,不同裂纹参数下T型裂纹梁与无裂纹梁上下表面的竖向位移(W),图4给出了裂纹位于跨中时,不同裂纹深度(h3/h=0、0.2、0.5、0.8)下梁的前两阶振型,图5给出了裂纹深度为h3/h=0.5,不同裂纹位置(l3/l=0.1、0.3、0.5)下梁的前两阶振型,其中,TS表示裂纹梁上表面的振型;LS表示裂纹梁下表面的振型。

(a) 一阶频率
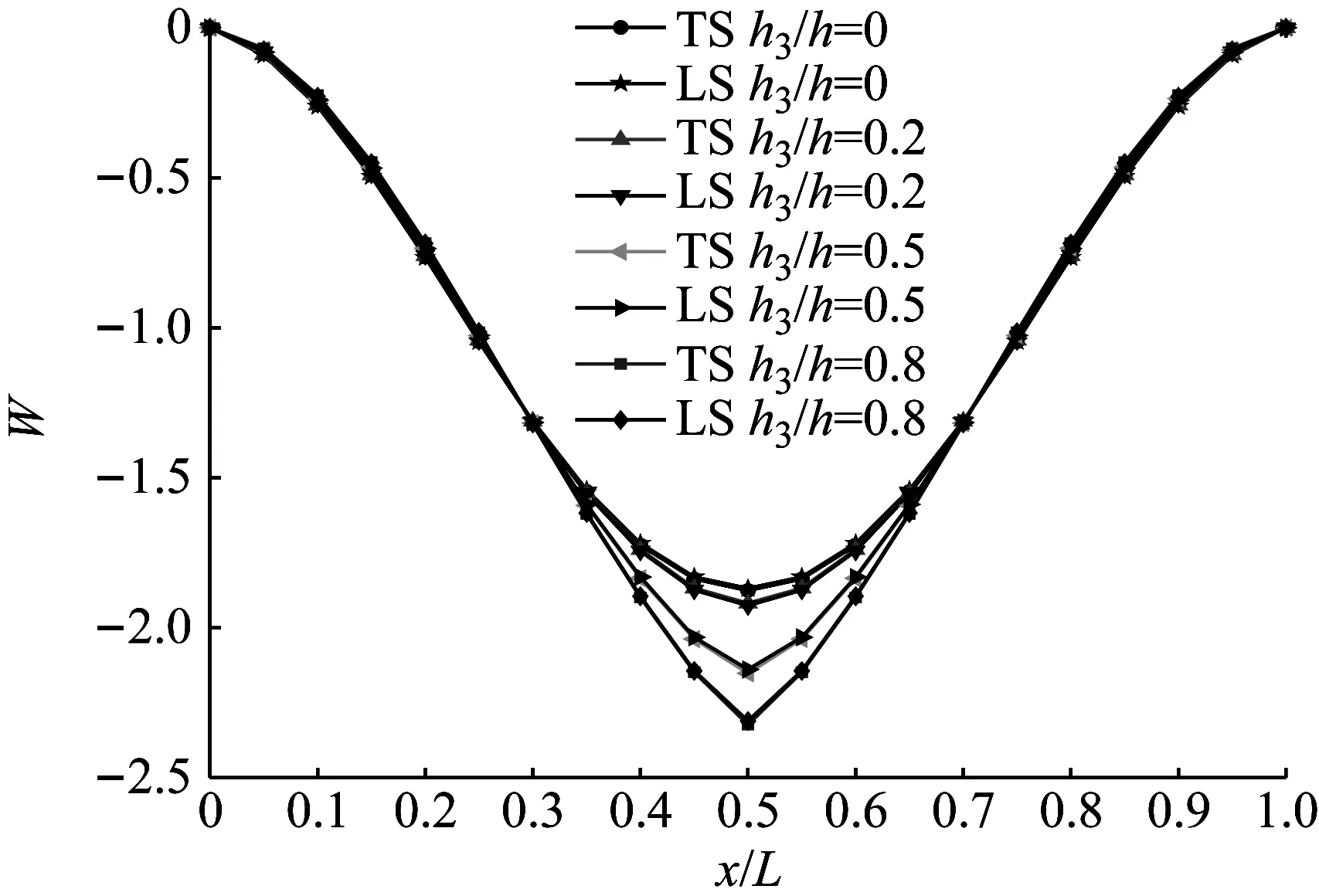
(a) 一阶振型
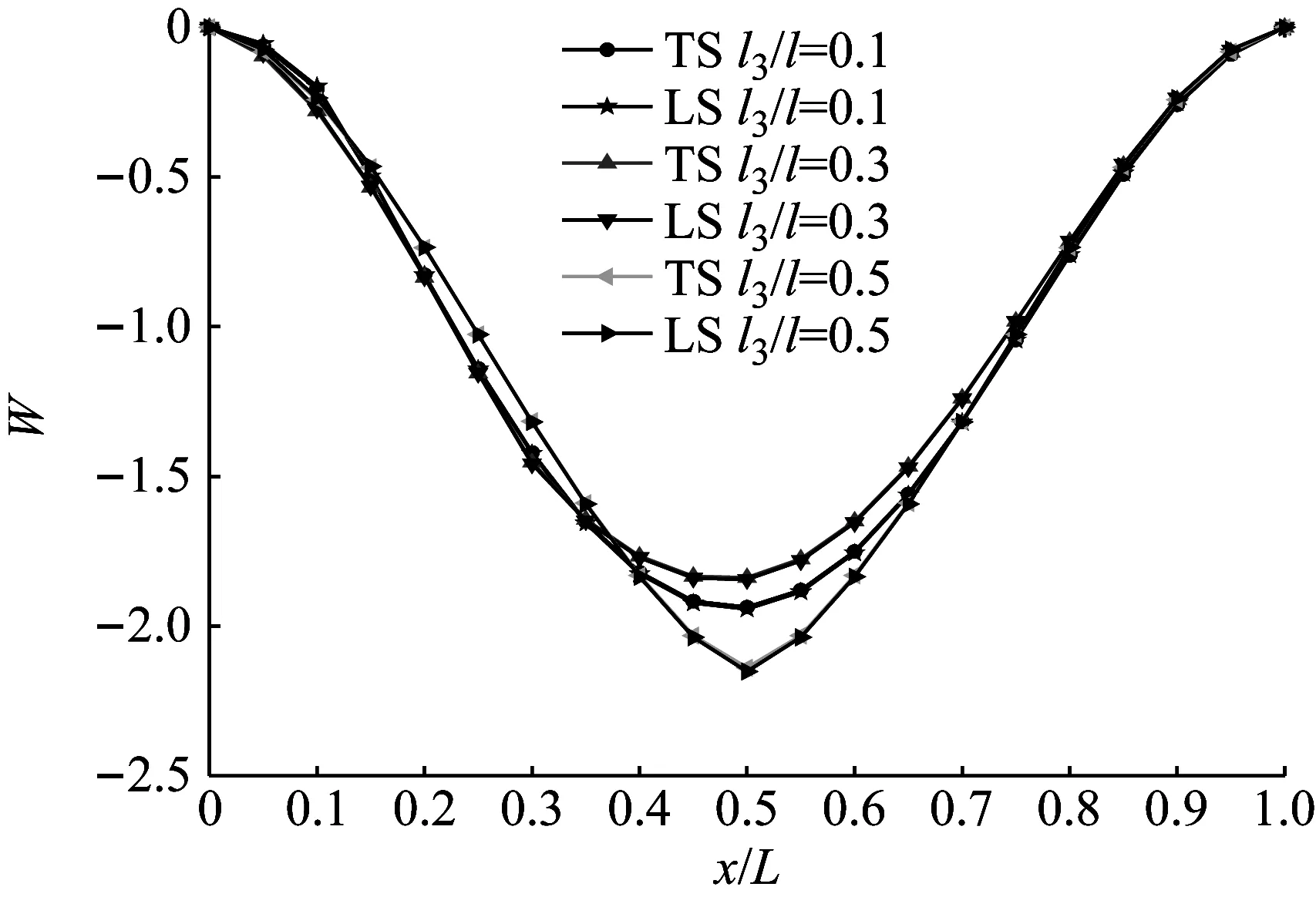
(a) 一阶振型
由图4可知,裂纹会增大梁上下表面振型的差异;裂纹梁的振幅随裂纹加深而增大,当裂纹位于跨中时对二阶振型的影响很小。由图5可知,裂纹位置对振型有影响,在其裂纹附近,振型会发生较为明显的改变。
5 结 论
本文基于二维弹性力学理论,利用Chebyshev-Ritz法研究含裂纹T型梁的自振特性,分析了裂纹参数(裂纹深度、裂纹位置)对T型裂纹梁振动特性的影响。与有限元计算结果对比吻合良好。研究数据表明:
(1) 裂缝的出现会导致梁各阶自振频率降低和各阶振型增大。
(2) 不同位置裂纹对T型梁振动特性的影响不相同,当裂纹位于跨中时,裂纹深度对一阶频率的影响最大,对二阶频率的影响不明显。
(3) 梁的振型在裂纹附近变化较为明显。
