部分埋置核心钢管组合桥墩抗震性能试验研究

李文武，邱文亮，田 甜，张 哲

(1.湖南省交通规划勘察设计院有限公司,长沙 410200;2.大连理工大学 建设工程学部，辽宁 大连 116024)

桥墩是梁式桥承重和抗侧向力的主要构件，也是地震作用下的易损构件，大量震害资料表明，严重的墩柱破坏是导致上部结构落梁、桥梁整体垮塌等灾难性后果的主要原因[1]。因此，提高桥墩的损伤容限和抗震性能是解决梁式桥抗震防灾能力不足的关键。基于对墩柱常见震害[2-3]及破坏机理的分析，Qiu等[4-5]提出一种新型抗震墩柱——钢管混凝土组合桥墩(以下简称常规组合桥墩)，其构造特点是在墩身内通长设置直径为墩柱截面尺寸1/3倍～1/2倍的圆钢管，从而形成一种以圆钢管为钢骨的钢-混凝土组合桥墩。该桥墩方案的抗震优势在于：利用钢管与核心混凝土结合后所形成的钢管混凝土芯柱轴压强度高和抗剪性能好的优点，以达到避免传统钢筋混凝土桥墩弯曲压溃和剪切脆断两类典型震害的发生并减轻墩身损伤的目的，同时实现对墩身变形和耗能能力的提升。另外，得益于钢管混凝土芯柱的支撑作用，桥墩的自复位能力及震后可修复性也可得到改善[6-8]。

对于大、中剪跨比(受弯破坏)的桥墩，其在地震作用下的滞回耗能主要依靠塑性铰的非弹性变形来完成，而墩柱中上部进入非线性的程度和损伤通常较轻。这种情况下，在墩身内通长设置核心钢管对整个墩身进行加强已无必要。此时，可仅在墩身中下部预埋核心钢管，以提高塑性铰区的抗弯、抗剪损伤容限以及塑性转动能力。鉴于此，在常规组合桥墩抗震研究的基础上，本文进一步提出了部分埋置核心钢管的组合桥墩方案，即只在距墩底一定高度的墩身范围内预埋核心钢管，并由此形成一种下部为钢管混凝土组合截面，上部为钢筋混凝土截面的墩柱构件，以期在改善结构抗震性能的同时不大幅增加钢材成本，从而较钢管通长设置的常规组合桥墩表现出更好的经济性。然而，部分埋置核心钢管组合桥墩的抗震表现究竟如何，能否达到预期的目的，是否具备应用于工程实践的可行性，尚需要进行研究。为此，本文开展了此类墩柱的抗震性能试验研究。

本文的主要研究内容包含以下三部分：① 探讨核心钢管埋置长度对部分埋置核心钢管组合桥墩失效模式和抗震性能的影响；② 通过与钢筋混凝土桥墩和常规组合桥墩试件的对比，以验证该墩柱方案的可行性，并得到在本次试验所采用的结构参数下最合理的核心钢管埋置长度；③ 以上述含有最合理钢管埋置长度的试件为基准件，进一步研究了轴压比、配箍率和核心钢管规格3个参数对部分埋置核心钢管组合桥墩抗震性能的影响。

1 试验概况

1.1 试件设计

共设计了8个剪跨比λ=3.0的圆形截面桥墩试件，各试件的参数汇总如表1所示。前期通过5个试件CE-STRC-E0～E4探讨了核心钢管埋置长度的影响，并完成了与钢筋混凝土桥墩和常规组合桥墩试件的对比。其中，CE-STRC-E1～E3为部分埋置核心钢管组合桥墩试件，三者的核心钢管长度l分别取为墩高h的1/3倍、1/2倍和2/3倍。CE-STRC-E0墩身内未设置核心钢管，为钢筋混凝土桥墩试件；CE-STRC-E4为常规组合桥墩试件，其核心钢管长度与墩高h相同。在完成上述5个试件的试验之后，后续又补充设计了3个试件CE-STRC-E2N～E2T，进而考察了轴压比、配箍率以及核心钢管规格对此类桥墩抗震性能的影响，三者的结构参数以CE-STRC-E2为基础作相应地变动，具体如下：① CE-STRC-E2N的结构参数与CE-STRC-E2保持一致，变量为轴压比；② CE-STRC-E2V的箍筋布置为Φ8@50，体积配箍率为1.18%；③ CE-STRC-E2T墩身内的核心钢管规格为Φ108×5 mm，截面含钢率为2.28%。

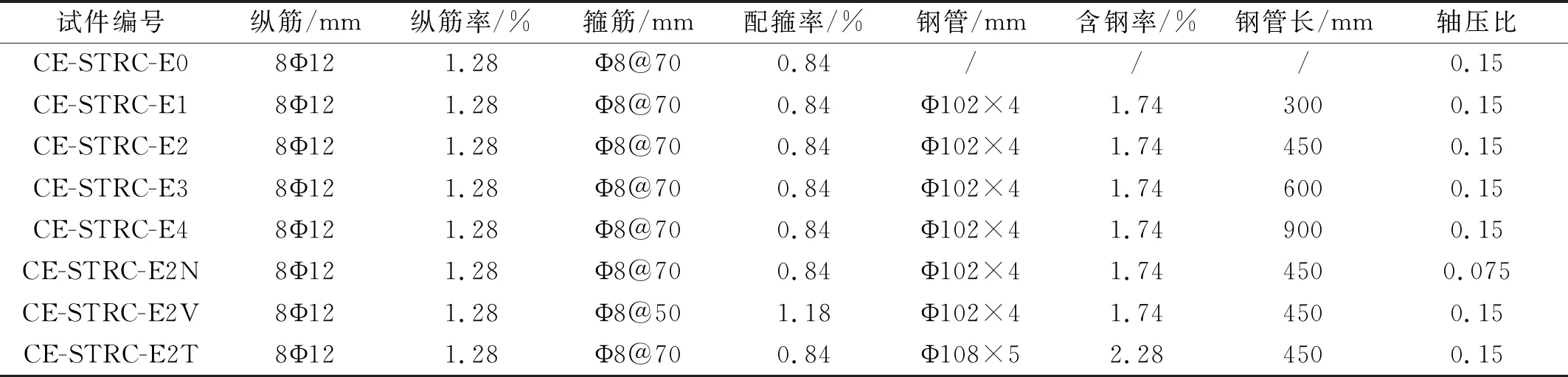
表1 试件设计参数汇总Tab.1 Summary of specimen parameters

桥墩试件的具体构造和配筋如图1所示。墩身截面直径为300 mm，墩柱总高为1 050 mm，有效高度为900 mm，试验区段剪跨比λ=3.0，墩柱下方为1 400 mm×600 mm×500 mm的钢筋混凝土长方体底座。墩柱纵筋为沿截面圆周均匀布置8Φ12的HRB400级热轧带肋钢筋，墩身螺旋箍筋采用Φ8的HPB300级光圆钢筋，箍筋间距分别为70 mm和50 mm；核心钢管采用规格为Φ102×4 mm或Φ108×5 mm的Q345无缝钢管。试验轴压比分0.15和0.075两种，施加于墩顶的竖向力分别为284 kN和142 kN。桥墩试件采用C40商品混凝土浇筑而成，混凝土立方体标准试块28天抗压强度为45.0 MPa；Φ102×4 mm和Φ108×5 mm两种规格钢管的屈服强度分别为368 MPa和351 MPa，极限强度分别为562 MPa和554 MPa；Φ12纵筋屈服强度极限强度分别为422 MPa和605 MPa；Φ8箍筋屈服强度和极限强度分别为450 MPa和550 MPa。

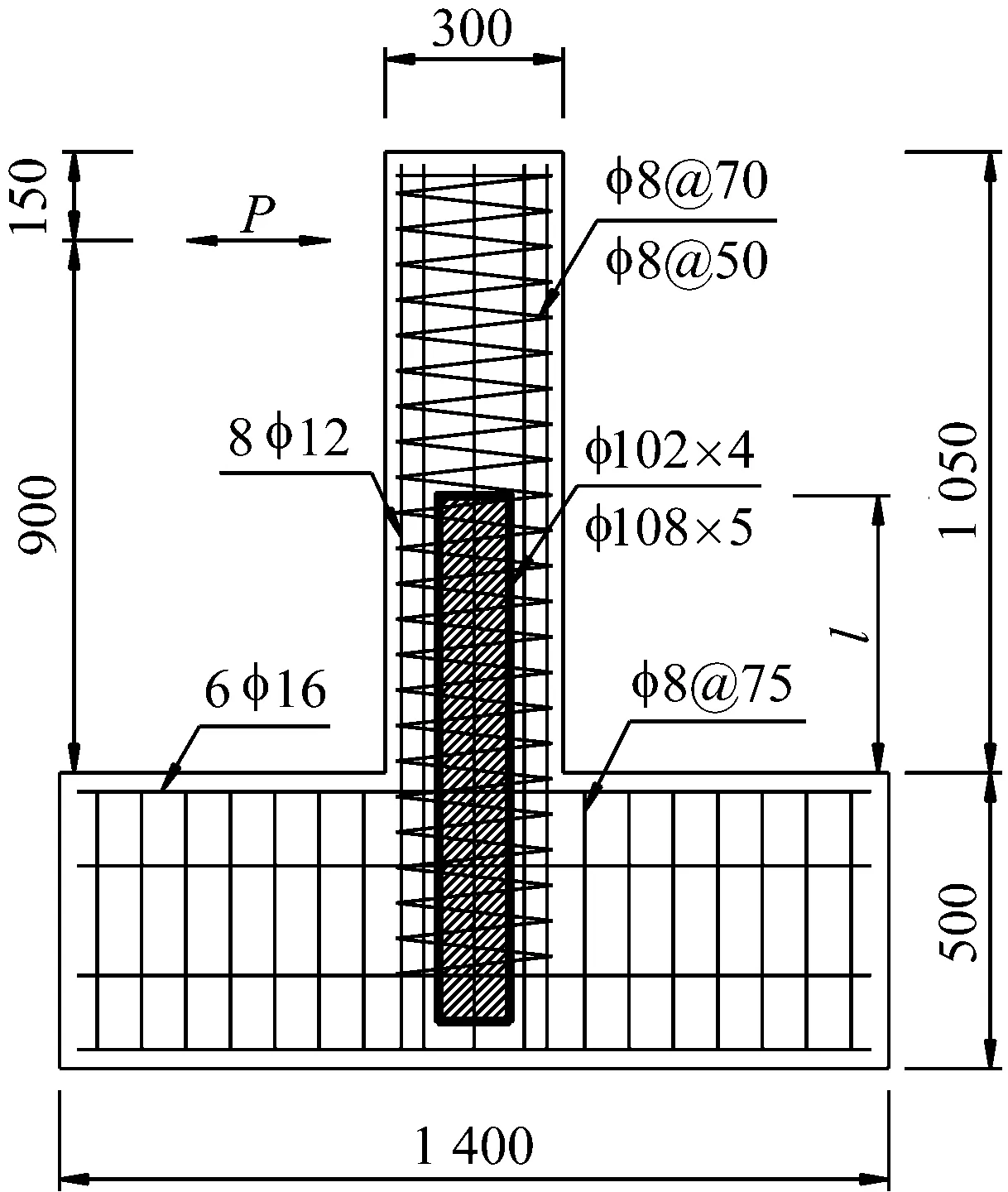
图1 试件尺寸及配筋图(mm)Fig.1 Dimensions and reinforcement layout of specimens(mm)

1.2 试验方案

试验装置如图2所示，采用悬臂式加载，以模拟实际桥墩底部为固结，顶部为自由端的边界条件。墩顶轴力由加载能力为3 000 kN的竖向千斤顶施加，千斤顶与反力架之间设有低摩阻滑槽，可使竖向顶随柱头平移而不偏转，以避免对柱头产生附加水平力。水平往复作用由电液伺服作动器施加，作动器缸体采用倒链悬吊在框架连梁上，以避免其自重对墩底产生附加P-Δ效应而影响试件的真实力学性能。作动器最大行程为±300 mm，加载能力为±1 000 kN，正向加载为推，反向加载为拉。水平作用的施加采用位移控制模式，加载历程依次为2 mm、4 mm、8 mm、12 mm、24 mm、36 mm，每级位移循环三次，当试件的水平承载力下降到最大值的80%以下或不适于继续加载时结束试验。水平作用施加速率较慢，每半个循环加载时间控制在2～5 min，总加载时间持续4～5 h。

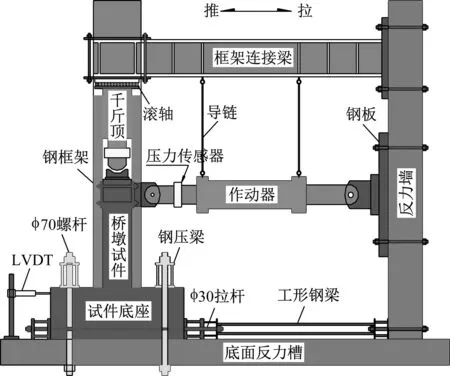
图2 试验加载装置Fig.2 Test set-up

1.3 数据采集

试验的主要目的是获取桥墩试件在往复荷载作用下的整体和局部响应，所以首先需要测量的数据是墩顶水平作用加载点处的荷载和位移；其次应详细记录如裂缝发展、保护层剥落、约束混凝土压溃以及纵筋屈曲、断裂等能定性描述墩身损伤演化的直观表象；第三，关键区域处纵筋、箍筋和核心钢管的应变等能定量反映墩身受力情况的信息也应进行监测；第四，为掌握墩身沿墩高的变形和曲率分布特征，需要分段量测墩身的水平、竖向和斜向变形。水平作用加载点处的荷载和位移由作动器的控制系统自动采集；应变和变形信号利用JM3813无线静态应变测试系统采集；墩身裂缝信息以及混凝土剥落情况采用混凝土裂缝探测仪、钢尺和量角器测量，并通过拍照记录。

2 试验现象及破坏机理

图3给出了各试件的最终破坏形态，照片中墩身水平标记线的间距为10 cm。从试验过程和破坏特征来看，8个试件在水平往复作用下发生的破坏模式主要可分为墩身中部剪切破坏、墩身中部弯曲破坏和墩底区域弯曲破坏三类。

(1) 对于核心钢管埋置长度为300 mm的试件CE-STRC-E1：Δ=4 mm时，首先在墩身下半段出现水平弯曲裂缝；Δ=8 mm时，水平裂缝朝墩身侧面斜向延伸，并生成若干斜向裂缝；Δ=12 mm时，钢管截断处(即钢管顶部)的水平和斜裂缝宽度陡然变大，而其余位置的裂缝宽度无明显增长；Δ=24 mm时，该位置处混凝土呈不规则的网状开裂并向外鼓出，同时破坏区域朝墩身上、下侧扩展，墩底混凝土也开始被压碎并成块剥落；Δ=36～48 mm时，墩身在钢管截断区域发生明显的脆性弯折，使得该位置附近的混凝土保护层大面积脱落，箍筋约束混凝土也严重受损。与此同时，墩底区域混凝土损伤也进一步加重，但其损伤程度要明显轻于钢管截断区域；Δ=60 mm时，纵筋于钢管顶部严重屈曲后疲劳断裂，试件承载力骤降，停止加载。虽然最终因纵筋被拉断而结束加载，但由于墩身斜裂缝发育充分，且破坏突然，该试件仍被判定为剪切破坏，并伴有严重的粘结劈裂破坏特征。

(2) 核心钢管规格较大的试件CE-STRC-E2T在墩身中部发生弯曲破坏，其损伤发展过程可描述为：Δ=4～12 mm时，墩身下半段出现水平弯曲裂缝并朝墩身侧面斜向延伸；Δ=24 mm时，距墩底100 mm及450 mm处的裂缝宽度明显增大；Δ=36 mm时，距墩底0～200 mm范围内保护层开始呈薄片状剥落。同时，距墩底400～500 mm处受拉侧裂缝宽度继续增加，受压侧出现竖向受压裂纹；Δ=48 mm时，墩底保护层剥落区域向上延伸，钢管截断处的竖向受压裂纹向下延伸，损伤区域逐渐汇合。至此，距墩底0～500 mm范围内的混凝土保护层都表现出明显的鼓起和剥落趋势；Δ=60 mm时，该范围内的混凝土保护层纷纷从墩身剥离。同时，钢管截断区域受损程度明显加重，墩顶水平位移相当一部分由墩身绕核心钢管顶部的转动提供，导致该位置处纵筋受压屈曲。而墩底区域的损伤发展则相对缓慢，纵筋屈曲程度较轻，箍筋约束混凝土基本完好；Δ=72 mm时，钢管截断处纵筋严重屈曲后疲劳断裂，停止加载。虽然CE-STRC-E2T墩身保护层脱落严重，但由于破坏前经历了较大的塑性变形，且破坏过程并不突然，因此被认为是弯曲破坏。

(3) 其余各桥墩试件均在墩底区域发生弯曲破坏，其损伤发展过程为：Δ=4 mm时，墩身下半部分500 mm范围内出现3～4条水平裂缝；随着水平荷载的增大，裂缝数量逐渐增多、间距变小，原有水平裂缝宽度变大，并朝墩身侧面斜向延伸直至相互交叉；Δ=8～12 mm时，纵筋和核心钢管相继受拉屈服。此后继续加载，裂缝数量不再明显增多，开始形成2～3条临界水平裂缝；Δ=24 mm时，试件的水平承载力达到峰值，此时墩底区域混凝土在压、拉反复作用下开始起皮、掉渣，并出现若干竖向受压裂缝；Δ=36 mm时，有呈片状的混凝土保护层开始从墩身剥离，且剥落范围和深度随着循环次数的增多而加大，试件的水平承载力逐步发生退化；Δ=48 mm时，墩底区域损伤程度继续加重，大块混凝土保护层被压碎、剥落，钢筋骨架外露；Δ=60 mm或72 mm时，墩底位置沿加载面最外侧两根纵筋被严重压曲、失稳，经几次循环后疲劳断裂，试件因承载力显著下降而宣告破坏，停止试验。

对于部分埋置核心钢管组合桥墩，在往复荷载作用下，外围钢筋混凝土通过挤压钢管混凝土芯柱迫使后者共同抵抗外荷载，这种挤压效应的反作用力相当于间接荷载作用于墩身内部，使钢管端部的外围混凝土处于双向拉、压的不利应力状态，会降低局部混凝土的力学性能并促成裂缝的生成。当钢管的埋长过短时(l≤300 mm)，钢管混凝土芯柱的侧向刚度大，其对外围混凝土的挤压作用强烈，使得局部混凝土力学性能退化严重。因此，该区域附近的斜向剪切和竖向劈裂裂缝充分发展，严重破坏了该部位混凝土的整体性，并进一步导致损伤和变形在钢管截断处集中发展。此时，核心钢管的加强作用未得到发挥就发生了诸如CE-STRC-E1的剪切破坏。而当钢管埋长较长时(l≥450 mm)，钢管混凝土芯柱的侧向刚度和所分担的水平力较小，其反作用力所引起的外围混凝土应力畸变程度较轻。与弯曲应力较大的墩底混凝土相比，虽然钢管端部混凝土的裂缝有所发展，但较轻的应力畸变所引起的局部混凝土受力性能劣化并不明显，因而损伤未集中在钢管顶部发展。另一方面，由于钢管截断引起的内力畸变区远离墩底区域，对塑性铰的转动能力影响很小。因此，核心钢管的加强作用得到充分发挥，相关试件(CE-STRC-E2/E3/E2N/E2V)表现出良好的变形能力。对于CE-STRC-E2T，虽然其核心钢管埋长同为450 mm，但由于钢管规格较大，钢管混凝土芯柱的挤压反作用力较为强烈，对局部混凝土的力学性能削弱明显。因此，损伤和变形于核心钢管顶部和墩底塑性铰区均有发展，但钢管顶部区域损伤程度较为严重。

3 试验结果与分析

3.1 墩身曲率分布

图4所示为三个典型破坏试件在加载过程中的墩身曲率分布曲线，根据设置在墩身两侧的四对竖向位移传感器的读数计算得到[9]。

从图4(a)可以看出，试件CE-STRC-E1在距墩底200～400 mm量测区段内的曲率要明显大于其余区段，该200 mm区段即为墩身严重损伤区域。当水平位移幅值Δ=24 mm时，该区域内墩身曲率开始陡增并超过墩底区域。此后，继续增大水平位移，墩身的脆性弯折集中于该薄弱位置发展，而墩底区域的变形则几乎停滞。进一步发现，在相同的墩顶水平位移增量12 mm下，图4(a)中各曲率分布曲线的间距呈增大趋势，这表明塑性变形在钢管截断处呈不稳定发展，破坏过程突然、不可控；对于在墩底区域发生弯曲破坏的试件，如图4(b)所示，以CE-STRC-E2为例，整个加载过程中，墩底附近区域的曲率始终大于墩身中上部，且图中各曲线基本呈等间距分布，表明塑性变形在墩底区域稳定发展，试件的破坏过程平稳、可控。对于核心钢管规格较大的试件CE-STRC-E2T，其墩身曲率分布则是处于上述两种情况之间，由图4(c)可见，在距墩底0～100 mm以及距墩底400～500 mm高度范围内的曲率较大，这与试验中观察到的墩身破坏情况一致。另外，各位移幅值下的曲率分布曲线间距差别不大，这也表明CE-STRC-E2T的损伤发展较为平缓，验证了前述判定其最终失效模式为弯曲破坏的合理性。值得注意的是，试验中、后期观察到CE-STRC-E2T绕墩身中部发生明显转动，但该区段的实测曲率反而较墩底区域要小，这主要是由于以下两个方面的原因：① 该量测区段较长(400～700 mm)，而墩底区域的量测范围仅为其1/3(0～100 mm)。因此，用实测转角除以量测区段的长度后就使得墩身中部测量区段的平均曲率值大幅减小；② 墩底0～100 mm范围内的测量转角还包含了纵筋在底座内因拔出效应所导致的墩身刚性旋转，从而使得墩底区段的实测曲率较真实值要大。

(a) CE-STRC-E0

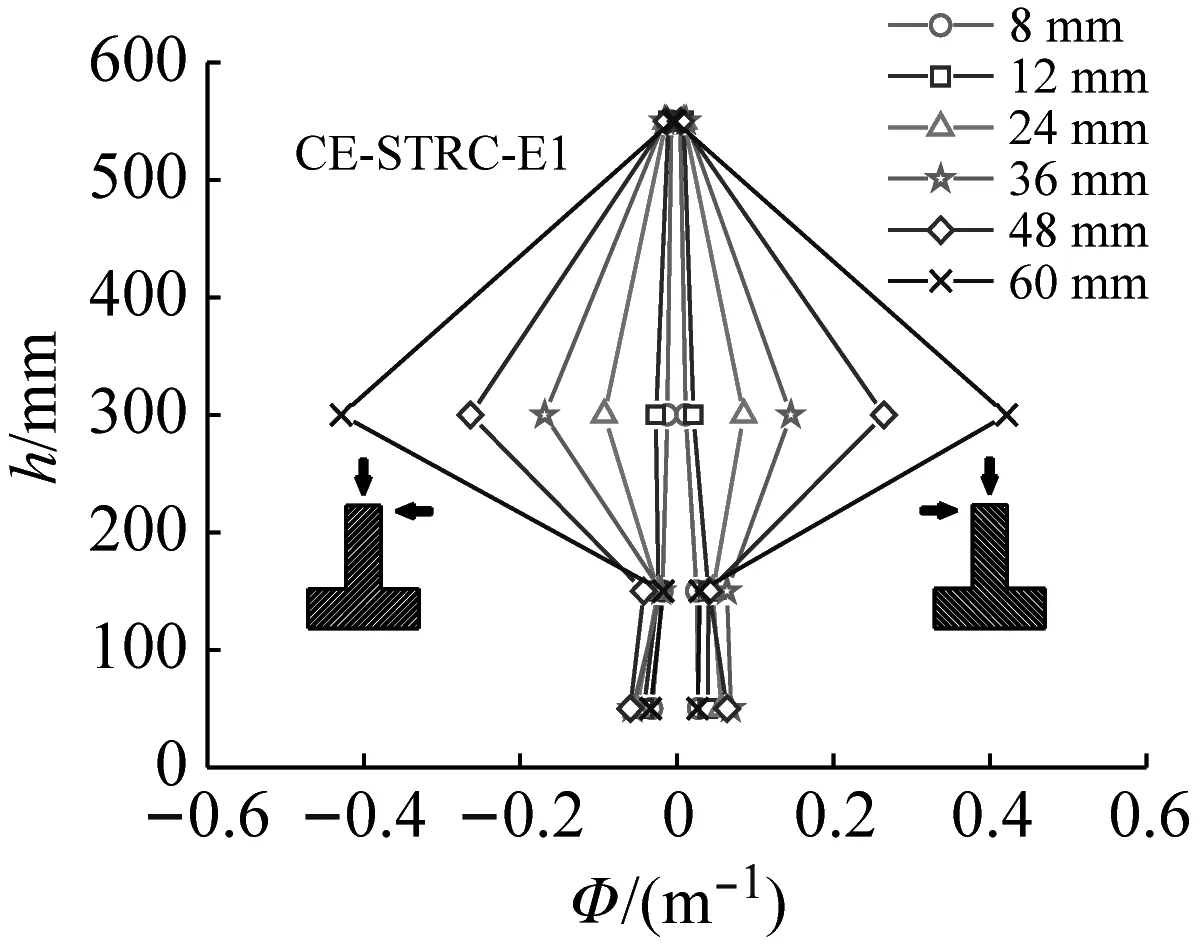
(a) CE-STRC-E1

(a) CE-STRC-E0

(a) CE-STRC-E0

3.2 滞回曲线

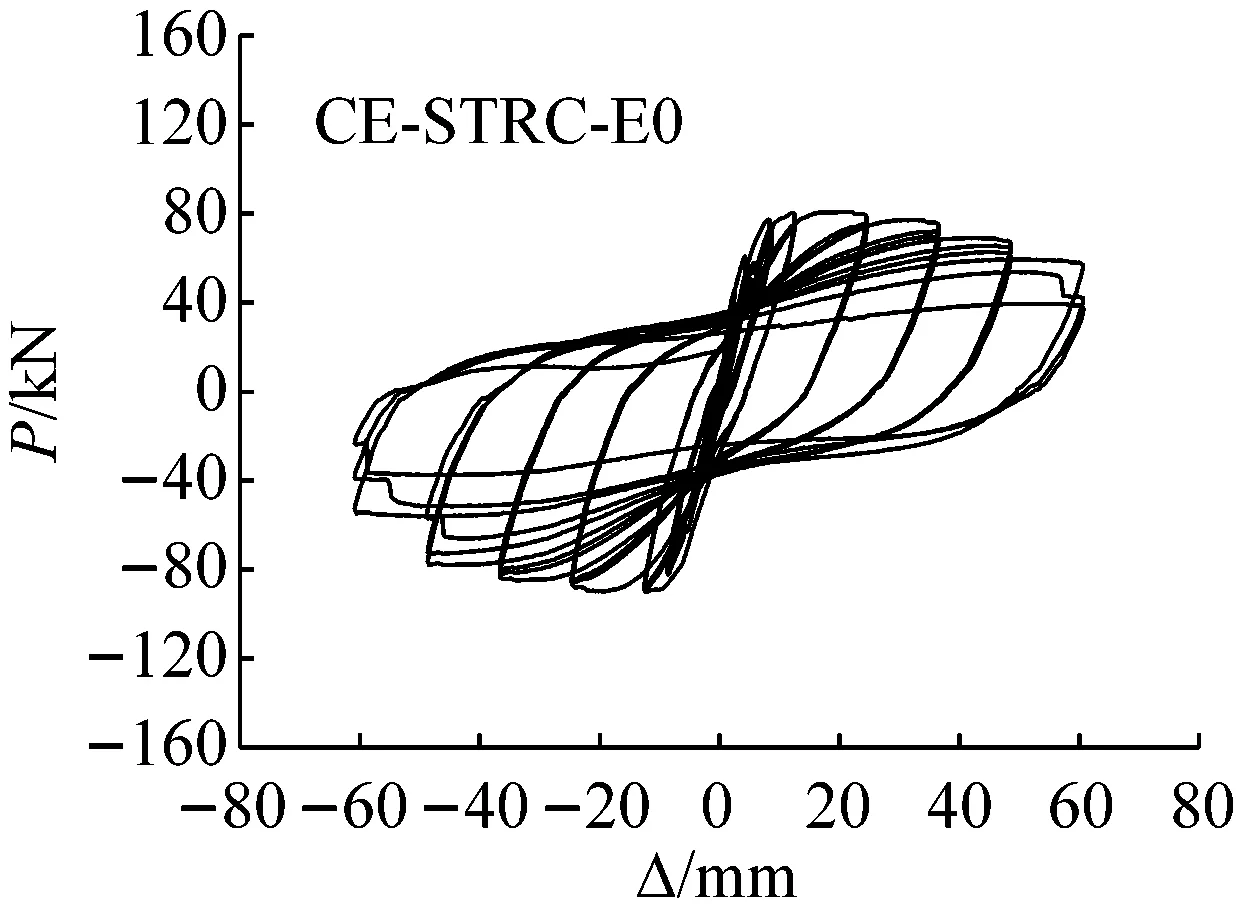
各试件的荷载-位移滞回曲线如图5所示。由图5可见：① 钢筋混凝土桥墩试件CE-STRC-E0的滞回环瘦小，捏缩、滑移现象明显，表明其滞回性能较差；② 常规组合桥墩试件CE-STRC-E4的滞回曲线则比较饱满，表现出较为稳定的滞回性能；③ CE-STRC-E2和CE-STRC-E3二者滞回曲线的外观与CE-STRC-E4差别不大，但进一步观察发现，随核心钢管埋置长度由CE-STRC-E2的450 mm增加到CE-STRC-E4的900 mm，滞回曲线的稳定性和饱满度均有所退化。相关研究表明[10-11]，墩身内部粘结裂缝的形成与发展是其根本原因：钢管与混凝土之间的粘结性能较差(通常为带肋钢筋与混凝土之间粘结强度的50%不到)，容易产生粘结裂缝，且核心钢管的埋置长度直接影响到粘结裂缝的状况——即钢管长度越长，钢管混凝土芯柱与外围混凝土界面上的粘结裂缝分布范围越广、发展越充分，从而导致二者之间的共同工作程度退化越快，试件抵抗反复荷载的能力以及滞回曲线的稳定性随之而变差。此外，粘结滑移还会加重滞回环的捏缩，这也从图5中有所体现；④ 对于钢管埋置长度为300 mm的CE-STRC-E1，在加载前、中期，其滞回环的饱满度较钢筋混凝土试件有所提高。但由于墩身剪切效应明显，破坏发展突然，最终在较小的水平位移下，滞回曲线就表现出发散和不稳定性，其滞回性能在所有试件中表现最差。

后期补充的3个试件核心钢管埋置长度均为450 mm，且各试件的结构参数根据研究变量以CE-STRC-E2为基础进行调整：① 对比CE-STRC-E2和CE-STRC-E2N可见，当轴压比由0.15降低到0.075时，虽然滞回曲线的捏缩效应加重，但试件在纵筋断裂前所经历的循环次数和位移幅值有所增加，且峰值荷载过后承载力的退化速率减慢，变形能力得到提高；② 对比CE-STRC-E2和CE-STRC-E2V，当箍筋间距由70 mm加密到50 mm时，滞回曲线所围成区域的面积增大，且纵筋疲劳断裂也有所延迟，试件的延性和耗能均得到改善；③ 当核心钢管规格由Φ102×4 mm增大到Φ108×5 mm时，滞回曲线的饱满度明显变好，表明试件的耗能能力得到提高，但加载后期滞回环的稳定性变差。

3.3 强度衰减

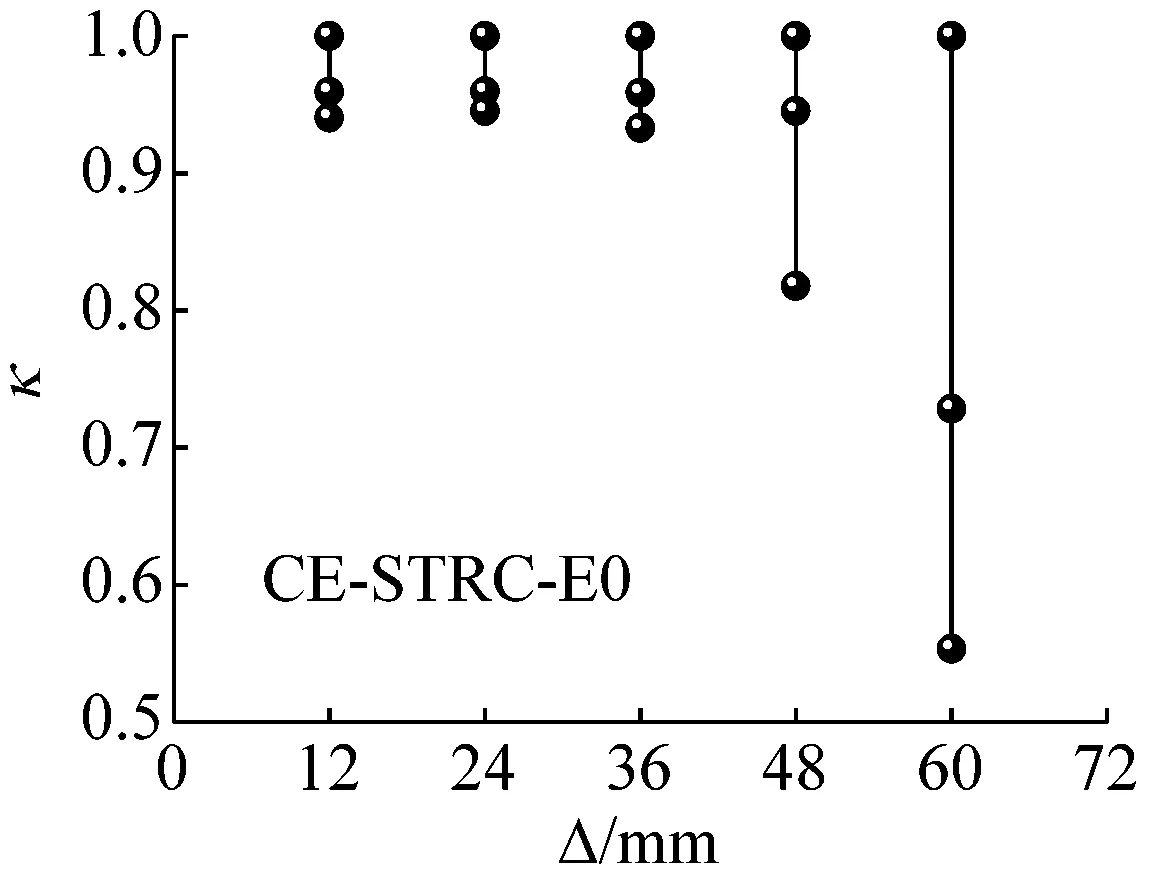
采用强度衰减系数κ，即某位移幅值下后两次循环的峰值荷载与首次循环的峰值荷载之比，来描述构件抵抗反复荷载的能力[12]。图6给出了各试件的κ值随水平位移Δ的变化曲线，由图6可知：① CE-STRC-E0在Δ=48 mm时强度衰减突然加快，衰减值为18%；Δ=60 mm时，衰减值达到45%。这表明钢筋混凝土桥墩抵抗大幅值位移循环的能力较差。② 对于剪切破坏的CE-STRC-E1，由于墩身损伤发展迅速，在Δ=48 mm时的强度衰减率即达到48%，其强度衰减的稳定性在所有试件中表现最差。③ 对于弯曲破坏的CE-STRC-E2～E3，Δ=60 mm时强度衰减率分别为15%和20%，二者强度衰减的稳定性要明显好于CE-STRC-E0和CE-STRC-E1。可见，当核心钢管在墩身内具有足够的埋置长度时，可显著改善试件抵抗反复荷载的能力。④ 对于常规组合桥墩试件CE-STRC-E4，Δ=60 mm时强度衰减率为21%，其强度衰减的稳定性要差于钢管埋置长度为450 mm的CE-STRC-E2，其原因已在第3.2节中解释。⑤ 对比CE-STRC-E2和CE-STRC-E2N，Δ=48 mm时，两个试件的强度衰减率均为8%；Δ=60 mm时，二者的强度衰减值分别为15%和10%。可见，加载后期的强度衰减随轴压比的增大有所加快。⑥ 箍筋间距为50 mm的CE-STRC-E2V在整个加载过程中的强度衰减非常稳定，Δ=60 mm时仅衰减8%，在所有试件中表现最好。可见，提高配箍率可明显提高试件抵抗反复荷载的能力。⑦ 钢管规格较大的CE-STRC-E2T在Δ≤48 mm时的强度衰减与CE-STRC-E2差别甚微；Δ=60 mm时，前者的强度衰减值达到24%，比CE-STRC-E2多9%。可见，增大核心钢管规格加剧了加载后期墩身的损伤发展。

3.4 骨架曲线

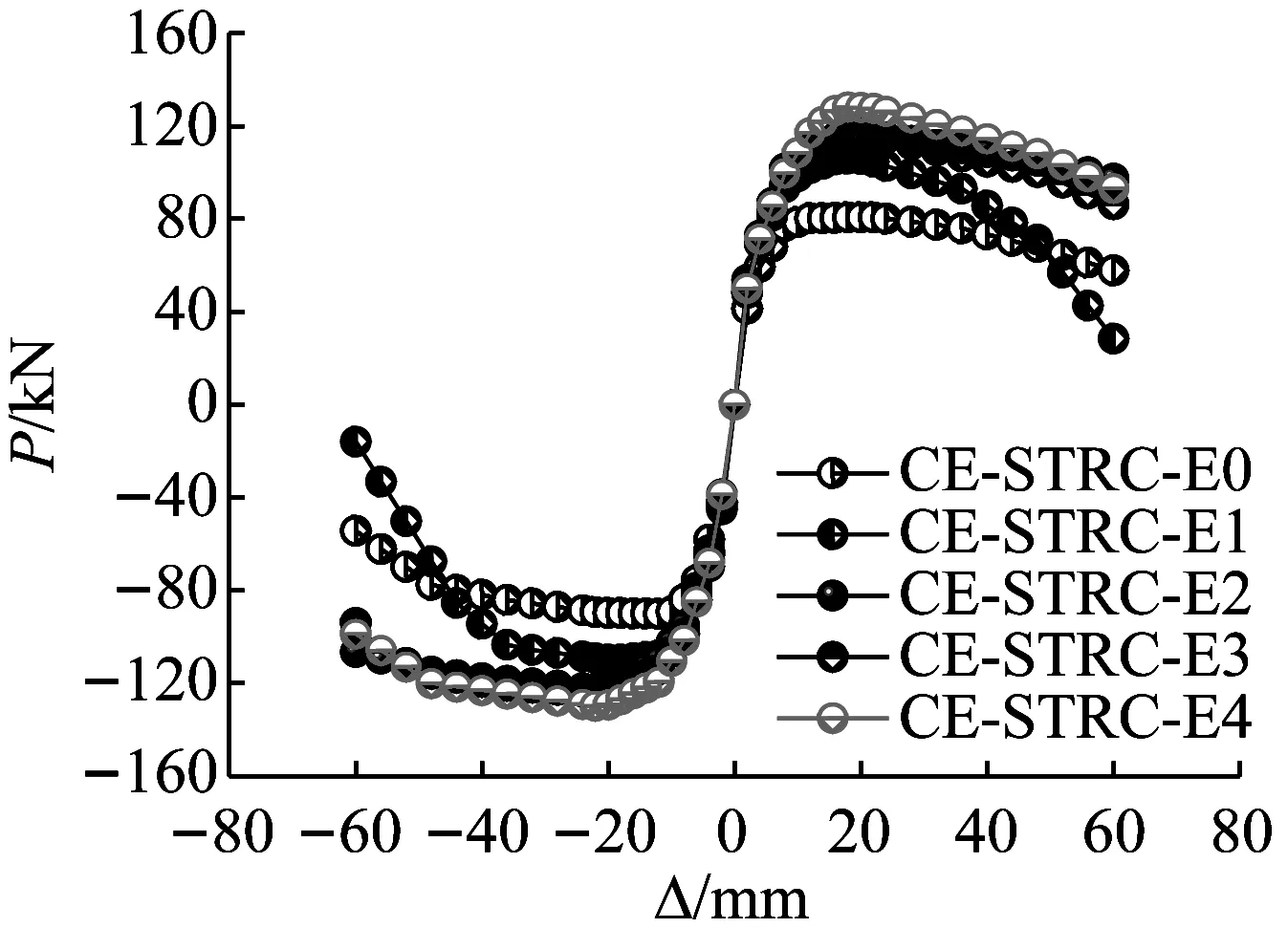
各试件的荷载-位移骨架曲线见图7所示。由图7(a)可见：① 钢筋混凝土试件CE-STRC-E0的水平承载力最低，但峰值点过后骨架曲线的下降段较为平缓；② 对比CE-STRC-E0和CE-STRC-E1可知，在墩身内埋置300 mm长的钢管后，试件的水平承载力大幅提高，但由于破坏模式发生改变，骨架曲线下降段变陡，墩身的变形能力反而较未设置核心钢管时要差；③ 当钢管埋置长度分别为450 mm、600 mm和900 mm时，相应的三个试件CE-STRC-E2～E4均发生弯曲延性破坏，三者的变形能力较CE-STRC-E1有显著提高。进一步观察发现，随钢管埋置长度的增加，骨架曲线的下降段变陡。这同样是由于核心钢管与外围混凝土之间粘结裂缝的发展所致，且核心钢管埋长越长，粘结问题越突出，峰值点过后承载力退化得越快。后续补充三个试件的骨架曲线与基准件CE-STRC-E2对比见图7(b)～7(d)：① 由图7(b)可见，当轴压比由0.15减小到0.075时，试件的水平承载力有所降低，但骨架曲线的下降段明显变缓，表明墩身的变形能力随轴压比的减小而提高；② 由图7(c)可见，当箍筋间距由70 mm减小到50 mm时，试件的水平承载力稍有提高。另外，由于箍筋加密对混凝土约束作用的增加，延缓了核心钢管与外围混凝土之间粘结性能的退化以及墩底受压区混凝土的剥落，因此峰值荷载后试件的承载力下降速度变慢，极限位移增大；③ 由图7(d)可见，当核心钢管由Φ102×4 mm增大到Φ108×5 mm时，试件的水平承载力得到提高。但增大钢管规格使芯柱与外围混凝土之间的相互挤压作用增强，局部混凝土的损伤加重，从而导致峰值点过后承载力退化加快，骨架曲线下降段变陡，墩身变形能力变差。

(a) 钢管埋置长度的影响

3.5 承载力和变形能力

各试件骨架曲线的特征点汇总见表2，表中数据为正、反向加载的平均值。其中，Pcr为墩身首次开裂点对应的荷载，Py和Δy为分别名义屈服点对应的荷载和位移，采用“Park法”确定[13]；Pm为峰值荷载，即试件的水平承载力；Δu为极限位移，取骨架曲线上水平承载力下降至最大值的85%时所对应的位移。极限位移角θu为Δu与墩高h的比值，位移延性系数μΔ为Δu与Δy的比值。由表2可见，除去受剪破坏的CE-STRC-E1，5个发生弯曲破坏的部分埋置核心钢管组合桥墩试件的极限位移角和位移延性系数均值分别为6.81%和6.88，可见此类桥墩具有优越的变形能力和位移延性。

表2 试验结果汇总Tab.2 Summary of experimental results

(1) 水平承载力分析：① 对于核心钢管埋置长度分别为300 mm、450 mm和600 mm的三个试件CE-STRC-E1～E3，其水平承载力较CE-STRC-E0依次提高了22.66 kN、33.81 kN和34.95 kN，增幅分别为26.5%、39.6%和40.9%。可见，在墩身内部分埋置核心钢管即可明显提升墩身的水平承载力；② 对比CE-STRC-E1和CE-STRC-E2，当钢管埋置长度由300 mm增至450 mm时，墩身的水平承载力随之增大。这是因为增加钢管长度可增大外围混凝土对钢管混凝土芯柱的挤压力臂，从而有助于提高钢管的弯曲正应力，以更好地发挥其抗弯加强作用；③ 对比CE-STRC-E2和CE-STRC-E3，二者的承载力差别甚微。这是由于当钢管埋置长度l=450 mm时，就可使芯柱基本达到弯曲屈服状态，抗弯强度得到充分发挥，此后再增加钢管埋置长度无法使其承担更多的外力，因而对继续提高水平承载力作用不大；④ 与CE-STRC-E4相比，CE-STRC-E3和CE-STRC-E2的水平承载力分别减小了8.53 kN和9.67 kN，降幅为6.6%和7.5%，在可接受范围之内。由此可知，部分埋置核心钢管桥墩其水平承载力可达到与常规组合桥墩相当的水平。对于后续补充设计的三个钢管埋长同为450 mm的试件：① 对比CE-STRC-E2和CE-STRC-E2N，当轴压比由0.15降至0.075时，承载力减小了9.58 kN，降幅为8.0%；② 对比CE-STRC-E2和CE-STRC-E2V，当箍筋间距由70 mm加密到50 mm时，水平承载力提高了4.60 kN，增幅为3.9%；③ 对比CE-STRC-E2和CE-STRC-E2T，当核心钢管规格由Φ102×4 mm增大到Φ108×5 mm时，水平承载力提高了10.22 kN，增幅为8.6%。综上可知，轴压比和核心钢管规格对水平承载力的影响较为明显，而配箍率的影响则相对较小。

(2) 变形能力分析：① 对比CE-STRC-E1～E3与钢筋混凝土桥墩试件CE-STRC-E0发现，核心钢管埋置长度为300 mm的CE-STRC-E1其极限位移比CE-STRC-E0还要小8.7 mm。这是由于其核心钢管的埋长不足，导致墩身的破坏模式发生了改变，这种情况下，非但达不到预期的改善效果，反而恶化了构件的变形性能。而对于钢管埋置长度为450 mm的CE-STRC-E2以及600 mm的CE-STRC-E3，由于钢管在墩身内埋长充足，试件发生弯曲延性破坏，钢管的抗弯加强作用得以发挥，因此二者的极限位移明显大于CE-STRC-E0。② 对比CE-STRC-E2～E3与CE-STRC-E4发现，当钢管埋置长度由CE-STRC-E4的900 mm减小到CE-STRC-E3的600 mm时，试件的极限位移反而增大了2.44 mm(+4.9%)；继续减小钢管埋置长度至CE-STRC-E2的450 mm，极限位移进一步增大了7.27 mm(+14.5%)。由此可见，在相同结构参数下，部分埋置核心钢管组合桥墩甚至具有优越于常规组合桥墩的变形能力。分别对比CE-STRC-E2N～E2T与CE-STRC-E2：① 当轴压比从0.15降至0.075时，极限位移增加了11.97 mm，增幅为20.0%，表明减小轴压比能显著改善此类桥墩的变形能力；② 当箍筋间距由70 mm加密到50 mm，极限位移增加了6.24 mm，增幅为10.4%，可见增大配箍率对变形能力的改善也较明显；③ 当核心钢管规格由Φ102×4 mm增至Φ108×5 mm，极限位移减小了3.22 mm，降幅为5.4%，可见增大钢管规格导致墩身的变形能力发生退化，由此建议此类桥墩核心钢管外径不宜超过墩身截面尺寸的1/3倍。

综合考虑承载力和变形能力两个基本性能指标，当核心钢管的埋长为450 mm时，墩身的变形能力达到最佳，同时具有较高的水平承载力。这也是后续补充3个试件的核心钢管埋长取为450 mm(即以CE-STRC-E2为基准件)的原因，并基于常规组合桥墩的相关研究结果，拟通过减小轴压比、增大体积配箍率和核心钢管规格来进一步发掘部分埋置核心钢管组合桥墩的抗震潜力。

4 水平承载力计算

水平作用下，外围钢筋混凝土通过挤压钢管混凝土芯柱将部分水平荷载传递给后者来承担，并由此实现二者的共同工作。对于外围钢筋混凝土而言，钢管混凝土芯柱对其存在挤压反作用力，该反力体现了芯柱对外围混凝土的支撑作用，相当于是对外围混凝土的侧向约束。芯柱对外围混凝土的侧向约束减小了墩身的实际剪跨比，使试件的水平承载力较钢筋混凝土试件有明显提高。上述力学特性分析为部分埋置核心钢管组合桥墩水平承载力的简化计算提供了一个新思路，其出发点是采用等效剪跨比λe[14]来替代构件的设计剪跨比λ，通过二者的比值λe/λ来反映芯柱的侧向约束对墩身水平承载力的提高程度，λe/λ越小，侧向约束效应越强，承载力的提高幅度越大。该方法的求解步骤为：① 对于给定的墩顶轴向力，首先将其分配给钢管混凝土芯柱和外围钢筋混凝土；② 求出钢筋混凝土环形截面在分配所得竖向力下的抗弯承载力Mrc；③ 根据结构和材料参数计算构件的等效剪跨比λe，其表达式将在后续讨论中给出；④ 将钢筋混凝土环形截面的抗弯承载力扣除掉竖向力P-Δ效应所产生的二阶弯矩后，再除以等效剪跨比λe与墩身直径D的乘积，进而得到墩身水平承载力的计算值，其结果亦为部分埋置核心钢管组合桥墩的水平承载力。下面介绍该方法的具体计算步骤。

步骤1钢筋混凝土部分分担的竖向力Nrc

外围钢筋混凝土部分所分担的竖向力根据其对整个墩柱轴向刚度的贡献比例进行分配[15]，并应考虑钢管的约束效应对核心混凝土轴向刚度的提高作用。

(1)

(2)

式中：Nstrc为墩顶轴向力设计值；Ecc、Eco和Acc、Aco分别为钢管内和钢管外混凝土的弹性模量和横截面面积；θ为钢管混凝土的套箍指标；fa、Aa分别为钢管的抗拉强度和钢管横截面面积；fcc为钢管内混凝土的抗压强度。

步骤2钢筋混凝土部分的抗弯承载力Mrc

外围钢筋混凝土部分在分配所得竖向力Nrc下的抗弯承载力Mrc可根据平截面假定和材料本构关系推导得出。但该计算过程过于复杂，不便于工程应用。通过将纵向钢筋等效为钢环，并采用等效矩形应力图替代受压和受拉钢环的应力分布，我国现行GB 50010—2010《混凝土结构设计规范》[16]给出了环形截面抗弯承载力的简化计算公式。计算时，先由式(3)求出受压区混凝土的面积比α，然后将α值代入式(4)即可求得外围钢筋混凝土环形截面的抗弯承载力Mrc。

Nrc=αfcoAco+(α-αt)fyAs

(3)

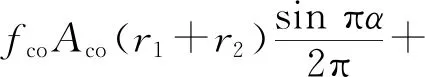
(4)

αt=1-1.5α

(5)

式中:fco、Ao分别为外围混凝土的抗压强度和横截面面积；fy为纵筋的抗拉强度；As全部纵向钢筋的截面面积；α为受压区混凝土截面面积与环形截面面积之比；αt为纵向受拉钢筋与全部纵向钢筋截面面积之比；r1、r2和rs分别为环形截面的内、外半径以及纵筋中心所在圆周的半径。

步骤3等效剪跨比λe

等效剪跨比λe反映了外围钢筋混凝土所受到侧向支撑的强弱，其本质上体现的是钢管混凝土芯柱侧向刚度K的大小，K越大，外围钢筋混凝土所受到的支撑作用越强，其λe值就越小，即λe与K呈负相关关系。K取决于核心钢管规格Φ和钢管在墩身内埋置长度的三次方l3，那么，K对λe的影响实际上间接反映了Φ和l3两个参数的综合对λe的影响。另外，通过分析具有不同核心钢管埋置长度l试件的试验结果可知，随l的增加，墩身的水平承载力随之提高，相当于λe在减小，这表明λe还受到l的直接影响，且λe与l呈负相关关系。其余两个试验参数，轴压比n和体积配箍率ρV，对芯柱的侧向刚度K无直接影响。但试验结果表明，随着n和ρV的增加，墩身的水平承载力均得到提升，这都相当于λe在减小，即λe与n、ρV同样呈负相关关系。根据以上所述，构造了以下表达式用于反映各研究变量对构件等效剪跨比的影响

(6)

K=3EI/l3

(7)

EI=EaIa+EccIcc

(8)

式中:η为l与h之比，即将核心钢管埋置长度l用墩高h进行归一化；EI为钢管混凝土芯柱的截面抗弯刚度；Ea、Ia和Ecc、Icc分别核心钢管和管内混凝土的弹性模量和截面惯性矩；a、b、c、d、α和β为由试验待定的参数，其中，前4个为常数或系数项，后2个为指数项。

需要说明一点，在构造式(6)的形式时，考虑到η(l)和K(Φ，1/l3)中均隐含了l，即l会从两个方面对λe产生影响，且l的轻微变化会引起1/l3的显著变化，并最终导致λe和Pm的剧烈变化，这与试验结果不符。故式(6)中分别将η和K配有指数项α和β，目的是希望拟合出α>1和0<β<1的结果，以均衡l和1/l3对λe的影响。

利用表3中的试验数据和计算结果对式(6)进行多元非线性回归分析，可得到以上各参数的取值依次为a=1.9，b=0.18，c=0.48，d=-2.5、α=1.1和β=0.26，即等效剪跨比的计算式为

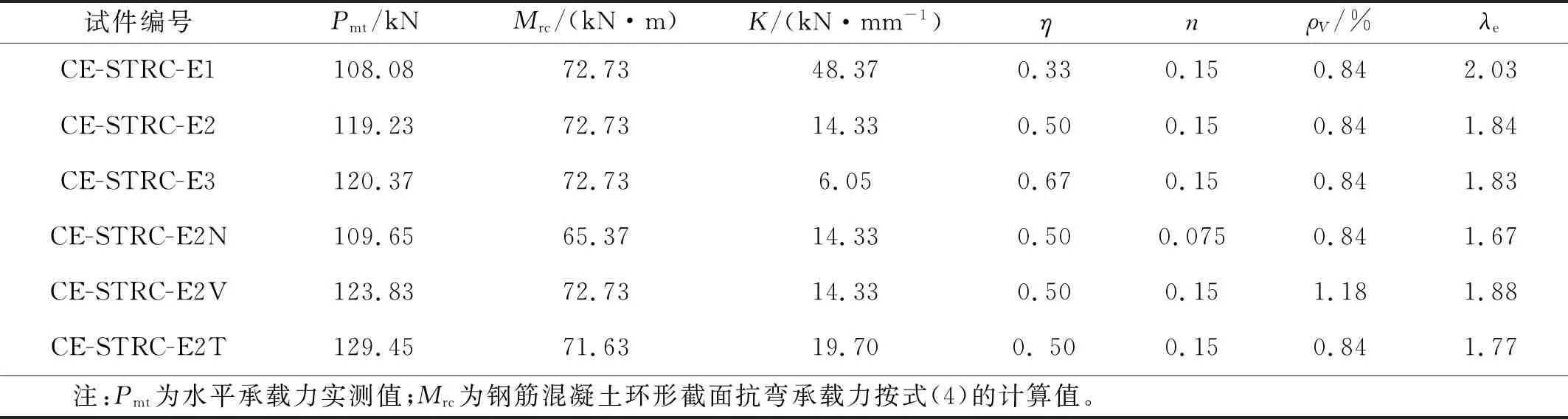
表3 参数回归用试验数据和计算结果Tab.3 Experimental data and calculated results for paremeters regressive

(9)

由式(9)可见，拟合所得的α和β值确实落在了所期望的区间内，达到了预期的目的；另外，参数b，c均为正值，说明前述分析的λe受ρV和n的影响规律同样正确。以上所述也表明本文所采用的等效剪跨比λe概念合理，所构造的λe关于各参数的表达式真实可信。

步骤4水平承载力计算

根据式(3)～(4)和式(7)～(9)分别计算出Mrc和λe后，再将二者代入式(10)即可得到部分埋置核心钢管组合桥墩的水平承载力Pmc

(10)

式中：D为墩柱截面直径；Δm为峰值点对应的水平位移。需要说明的是，实际设计中用式(10)进行计算时，Δm受结构参数和地震动的影响无法提前预知，导致计算过程受阻，这时可将反映竖向力二阶效应的NstrcΔm作为一个整体从Mrc中扣除。根据本次试验结果可知，当n=0.075时，NstrcΔm/Mrc=5.2%；当n=0.15时，NstrcΔm/Mrc=9.4%。因此，在桥墩常处于的轴压比范围内(n=0.05～0.15)，NstrcΔm/Mrc可根据以上数据采用线性插值或适当外延的方法来求得。总体来看，竖向力所产生的附加弯矩在墩底总弯矩中所占的比例较小，上述处理方法一般不至于引起太大误差。

步骤5计算结果验证

用步骤1～4对本次试验中6个部分埋置核心钢管组合桥墩试件的水平承载力进行计算，表4给出了计算值Pmc与试验实测值Pmt的对比，二者之比Pmc/Pmt的均值为0.97，均方差为0.003。可见，公式计算值与试验值非常接近且均在偏安全一侧，表明本文所给出的简化计算方法可用于部分埋置核心钢管组合桥墩的水平承载力预测。但需要说明一点，由于本次试验试件数量有限，样本空间所覆盖的参数范围较小，今后尚需要更多的试验结果，以进一步检验该方法的可靠性。

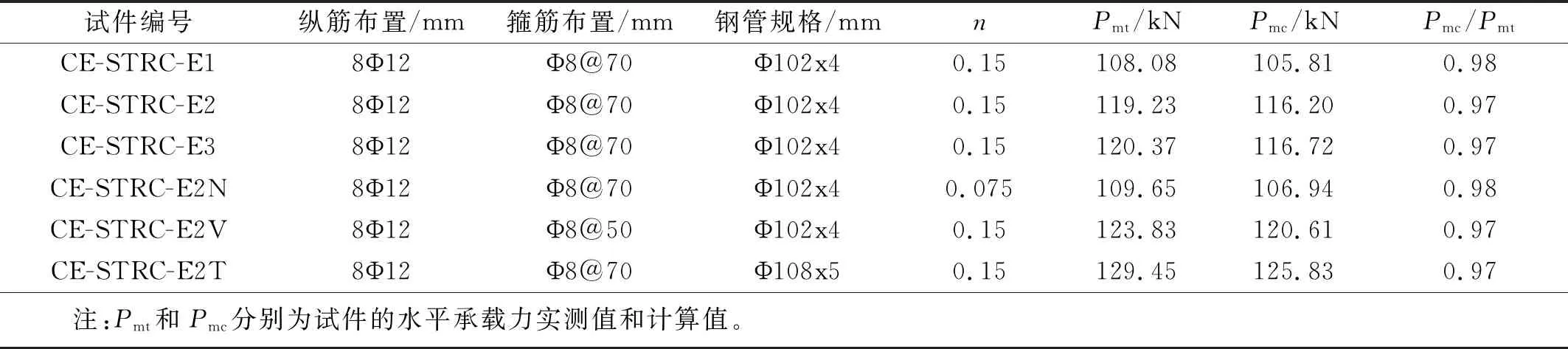
表4 试件水平承载力计算值与实测值对比Tab.4 Comparison of calculated and experimental column lateral resistance

5 结 论

通过8个桥墩试件的拟静力试验，研究了部分埋置核心钢管组合桥墩在往复荷载作用下的破坏模式和力学特性，主要结论如下：

(1) 核心钢管埋置长度是影响试件破坏形态和受力性能的重要参数。当钢管埋长不足时，墩身于钢管顶部发生剪切破坏，试件的滞回性能明显劣于钢筋混凝土对比件；当钢管埋长充足时，试件于墩底区域发生弯曲破坏，其滞回性能较钢筋混凝土桥墩有明显提升。此外，墩身的损伤发展还受到核心钢管规格的影响，钢管规格过大，也容易导致局部破坏的发生，对桥墩抗震反而不利。

(2) 部分埋置核心钢管组合桥墩的水平承载力明显高于钢筋混凝土桥墩对比件，且随钢管埋置长度的增加，试件的水平承载力逐渐提升。当钢管埋置长度增加到可使钢管混凝土芯柱基本达到弯曲屈服时，继续增加钢管长度对承载力的提高作用不大，但滞回曲线的稳定性变差，试件强度衰减加快。另一方面，试件的极限位移随钢管埋置长度的增加呈现出先增后降的变化趋势。

(3) 核心钢管的埋长并非越长越好，对于本次试验，当埋置长度为0.5倍墩身有效高度时，试件的各项抗震性能指标综合达到最优，其水平承载力较常规组合桥墩试件仅降低了7.5%，而极限位移却提高了19.4%，且强度衰减速度减慢。以上所述体现了部分埋置核心钢管桥墩方案其经济性和耐震性相统一的特点，从而验证了本文研究初衷的正确性以及该桥墩方案的可行性。

(4) 在其它结构参数相同的情况下，轴压比大的试件滞回曲线较为饱满，水平承载力高；但峰值点过后骨架曲线下降段坡度大，墩身变形能力差。增大配箍率对水平承载力的提高作用不大，但能明显改善试件的变形能力，同时降低强度衰减的速率。随核心钢管规格的增大，滞回曲线的饱满度变好，水平承载力得到提高；但加载后期墩身损伤程度加重，变形能力变差。

(5) 采用等效剪跨比来反映各设计参数对墩身水平承载力的影响具有概念清晰、简明实用的特点；以等效剪跨比作为中间变量来建立部分埋置核心钢管桥墩的水平承载力计算公式可绕开复杂的机理分析，且无需判别构件的失效模式。但由于本次试验试件数量有限，所建立公式的有效性和适用范围还有待进一步验证。