循环荷载下混凝土开裂-闭合行为计算方法研究
2021-05-17李晓琴
李晓琴,张 田
(昆明理工大学 建筑工程学院,昆明 650500)
随着有限元理论和计算技术的发展,有限元数值模拟方法已成为研究各种受力情况下RC结构响应的主要手段之一。ABAQUS中的CDP模型因具有较好的屈服准则、流动法则和滞回准则被广泛用于各类RC结构的抗震分析[1]。相对主要用于单调荷载下分析的脆性开裂模型[2]和弥散裂缝模型[3],CDP模型通过引入损伤参数(dt、dc)和刚度恢复因子(wt、wc)来分别描述混凝土在卸载时表现出的刚度退化和应力反转时混凝土存在的刚度恢复现象[4],该模型能较好地模拟循环荷载下混凝土的力学特性,如循环荷载下混凝土的开裂与压碎、裂缝张开与闭合、拉压应力反转和损伤累积等特征。然而,对于有限元分析,定义合理的材料参数是模拟结果正确反映真实结构力学行为的关键所在。
目前,大量学者对CDP模型的材料参数进行了相关研究,如Syed等[5]对混凝土本构关系中的膨胀角Ψ与参数wt、wc的组合取值给模拟结果带来的不确定性进行了研究;Yu等[6-7]对CDP模型采用的非关联塑性流动势和Drucker-Prager屈服准则进行了详细讨论;Alfarah等[8]基于混凝土破碎断裂能Gc和开裂断裂能GF阐述了混凝土单轴受压、受拉材料参数的计算;聂建国等对CDP模型的单轴应力-应变关系和裂缝模型等做了详细介绍。事实上,在CDP模型中,除了以上的材料参数需要明确以外,损伤参数(dt、dc)和刚度恢复因子(wt、wc)的确定也需要关注,对于损伤参数进行相关研究中,Alfarah等基于Gc和GF推导了新的拉压损伤计算公式;Long等[9]采用累计耗散能与断裂能的比值来建立损伤计算模型;方自虎等[10]基于软化应力与峰值应力的比值建立了适合于高强混凝土模拟分析的损伤计算公式;Birtel等[11]基于试验数据建立了与混凝土塑性应变有关的损伤计算公式;曹明[12]以能量等价原理为基础,并结合GB 50010—2010《混凝土结构设计规范》中提供的混凝土应力-应变曲线建立了损伤参数计算公式。然而,在CDP模型众多材料参数中,针对描述循环荷载下混凝土开裂-闭合行为的受压刚度恢复因子wc的取值至今未有深入研究。目前一些关于wc的研究工作主要有:Syed等研究指出wc取值很难直接从试验中直接测试得到,wc取值需要通过对比模拟与试验结果来标定;Zhao等[13]着重考虑wc对洞室结构动力特性的影响,研究发现当wc取值增大时洞室的损伤面积呈线性减小;尽管Karimi等[14]取wc=0.3来模拟填充墙和拱形砌体墙在循环荷载下的力学响应,虽然两个有限元模型的模拟值与试验结果的均具有较好的吻合度,但对wc的取值原因尚未说明;Alfarah等[15]为了模拟RC结构中严重破损区域处裂纹闭合时刚度恢复较小的现象,采用较小wc值定义构件严重破损区域。显然,对于wc的取值与应用问题,目前还没有足够的研究以一致的解决方法,这给CDP模型准确预测和模拟循环荷载下RC结构的力学响应带来了困难,尤其是在模拟对象尚未完成试验的情况下。
鉴于此,为解决上述问题,本研究针对wc的计算方法展开了理论研究和数值模拟,首先建立了考虑开裂断裂能GF的指数型软化应力-开裂位移曲线,并在现有的拉/压损伤计算模型中比选出适用于钢筋混凝土结构分析的损伤计算模型。在此基础上,以受拉残存断裂能密度gFR与开裂断裂能密度gf之比的θ次方(θ≥1)建立了wc计算模型,该模型同时考虑了单元特征长度leq和dt对wc的影响,并以单个单元为例说明了参数θ对wc的影响。进一步地,以循环荷载下严重破损RC节点为研究对象,基于现有混凝土裂缝特征与受拉损伤状态的统计关系[16],提出了一种基于拉伸损伤水平dt的模型简化处理方法,以此解决ABQUAS中CDP模型wc只支持某一常数所存在的局限性。通过对多组循环荷载下的RC节点进行了数值模拟并与试验数据比较,验证了循环荷载下混凝土开裂-闭合行为计算方法的正确性以及循环荷载下有限元模型简化处理方法的可行性。
1 CDP模型

图1(a)显示了混凝土单轴受拉时的力学行为,认为混凝土包括弹性阶段(0~σt0)和软化阶段(下降段)。当混凝土超过破坏应力σt0时,混凝土将进入软化和刚度退化阶段。图1(b)显示了混凝土单轴受压时的力学行为,认为混凝土受压时分别经历了弹性阶段(0~σc0)、强化阶段(σc0~σcu)和软化阶段。
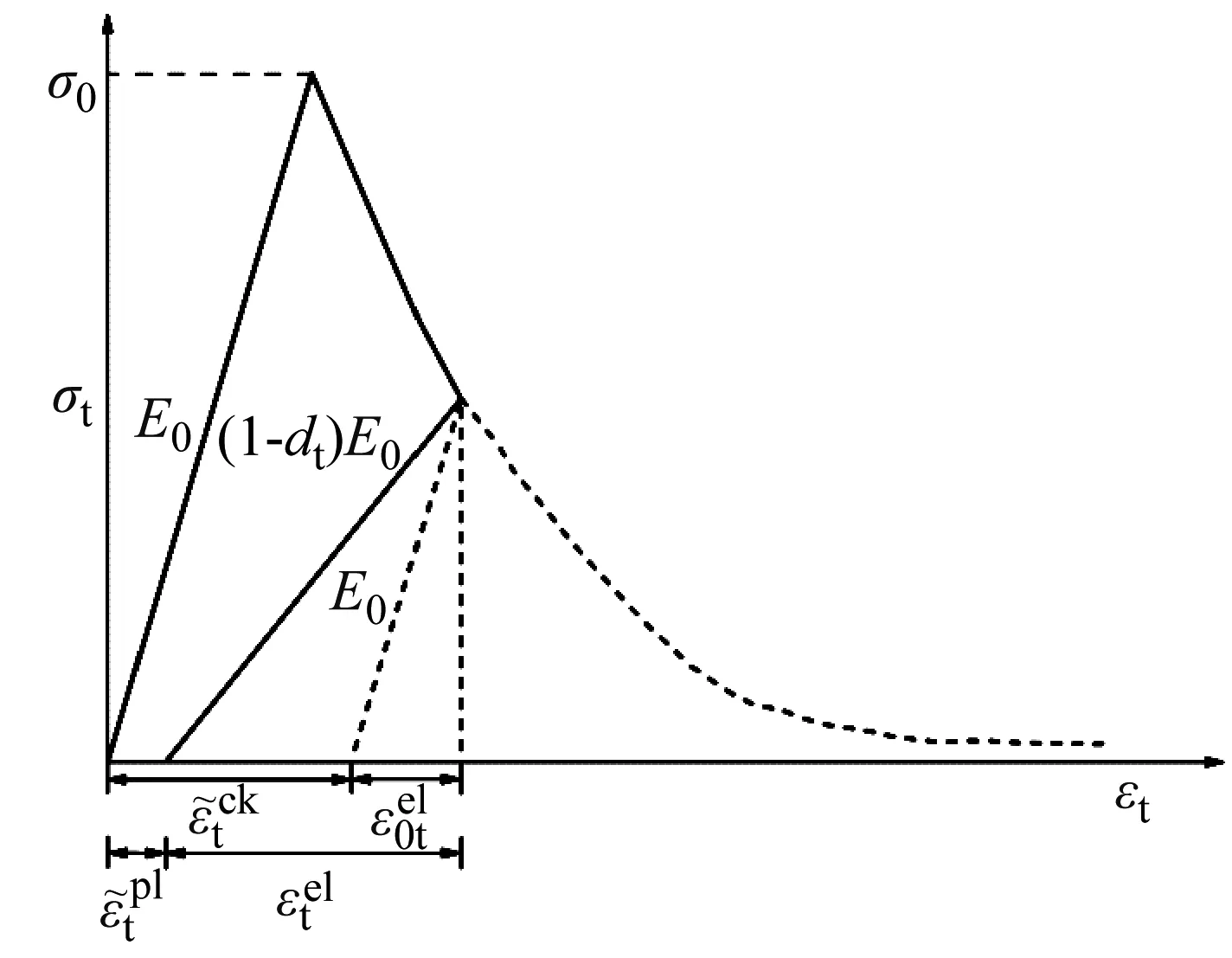
(a) 受拉
现假定E0为材料的初始弹性刚度,则上述的应力-应变关系可用式(1a)~(1b)描述。
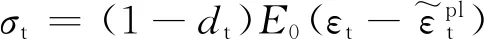
(1a)

(1b)


(2a)
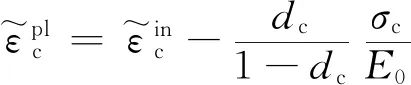
(2b)

(3a)
(3b)

试验表明,在单轴循环荷载下,荷载改变方向后材料的弹性刚度将得到部分恢复[20-21]。CDP模型引入刚度退化变量d描述混凝土的刚度退化行为,其中刚度退化变量d是关于应力状态和拉压损伤变量的函数。
E=(1-d)E0
(4)
(1-d)=(1-stdc)(1-scd)
(5)
式中:st和sc为考虑应力方向和刚度恢复效应的应力状态函数,根据式(6a)~(6b)确定。
st=1-wtr*(σ11) 0≤wt≤1
(6a)
sc=1-wc(1-r*(σ11)) 0≤wc≤1
(6b)
式中:wt和wc分别为受拉、受压刚度恢复因子,分别表示混凝土从受拉过渡到受压和从受压过渡到受拉时混凝土刚度的恢复程度;r*(σ11)为混凝土单轴应力因子,是主应力状态的函数,由式(7)确定。
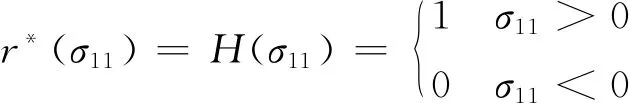
(7)
式中:σ11为混凝土的主应力状态,σ11>0表示受拉,σ11<0表示受压。
以单轴工况为例,CDP模型关于循环荷载下混凝土的应力-应变曲线如图2所示。
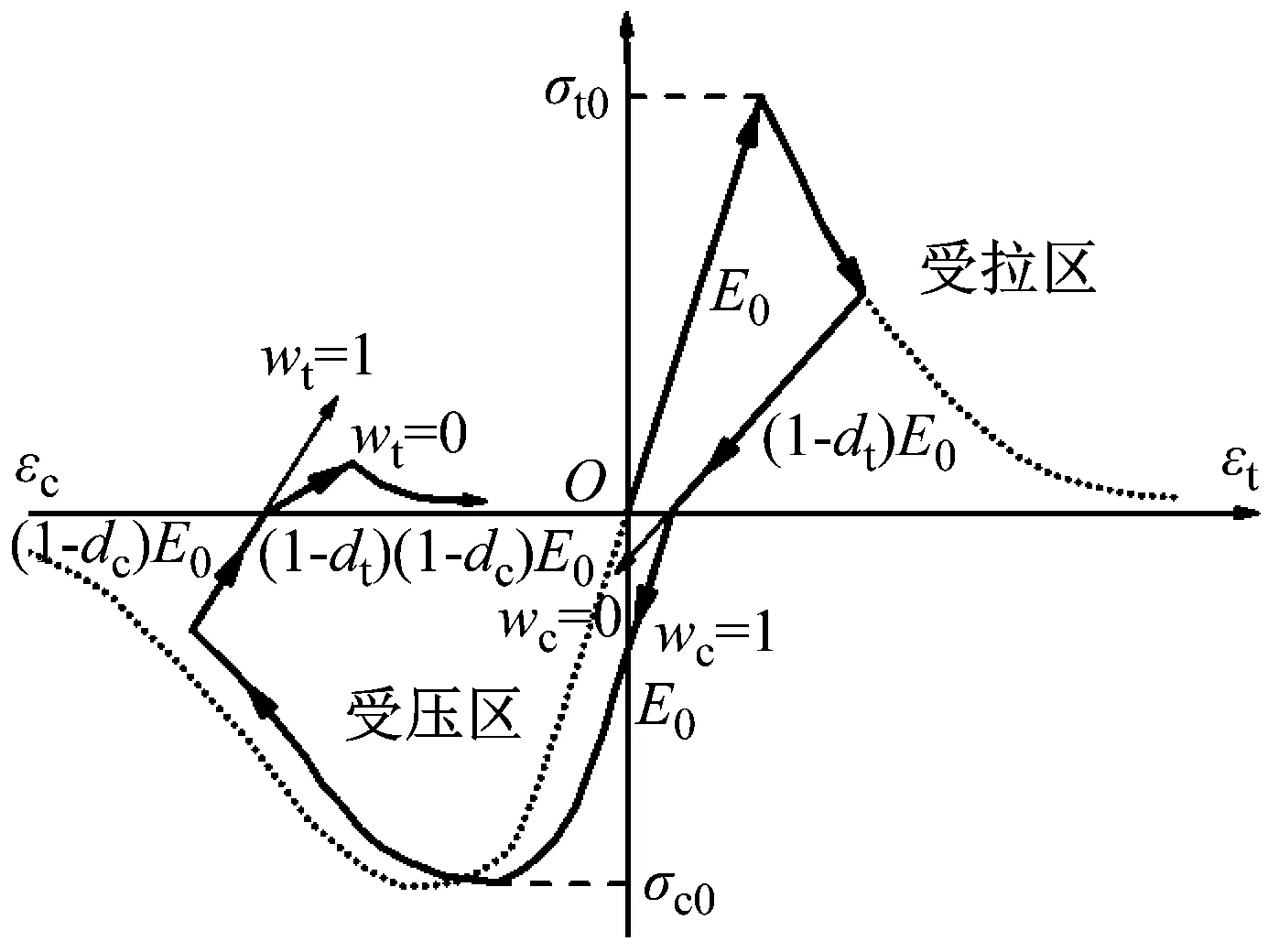
图2 单轴循环荷载作用下应力-应变关系(默认刚度恢复因子wt=0、wc=1)Fig.2 The stress-strain relationship under uniaxial cyclic loading (wt=0,wc=1)
CDP模型的塑性流动假定为非关联流动,塑性势G采用Drucker-Prager双曲线函数描述。
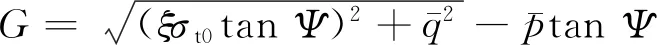
(8)
式中:Ψ为高围压下在p-q面上的膨胀角(对混凝土取值在25°~35°区间,本文模型采用30°);ξ为偏心率(默认值0.1),表示该函数接近渐近线的速率(当偏心率趋于零时,流动势趋于直线)。

(9)
式(9)中,各参数的计算公式如下

2 混凝土单轴受拉/抗压本构关系
混凝土的单轴受压力学行可通过三段函数定义,第一段为线弹性阶段式(11a);第二段为强化段[22]式(11b);第三段为软化段[23]式(11c)、式(11d)。
σc=E0εc
(11a)
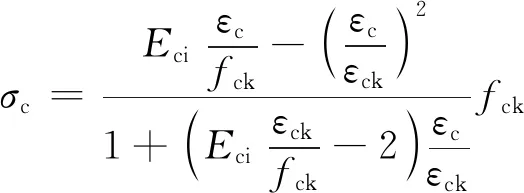
(11b)
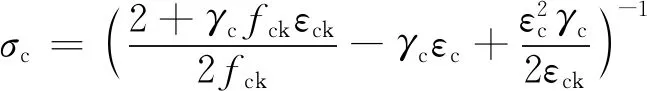
(11c)

(11d)

对于混凝土的单轴拉伸力学行为,本研究基于混凝土的开裂断裂能GF提出了适用于混凝土非线性分析的指数型软化段应力-开裂位移曲线(图3),其表示如下
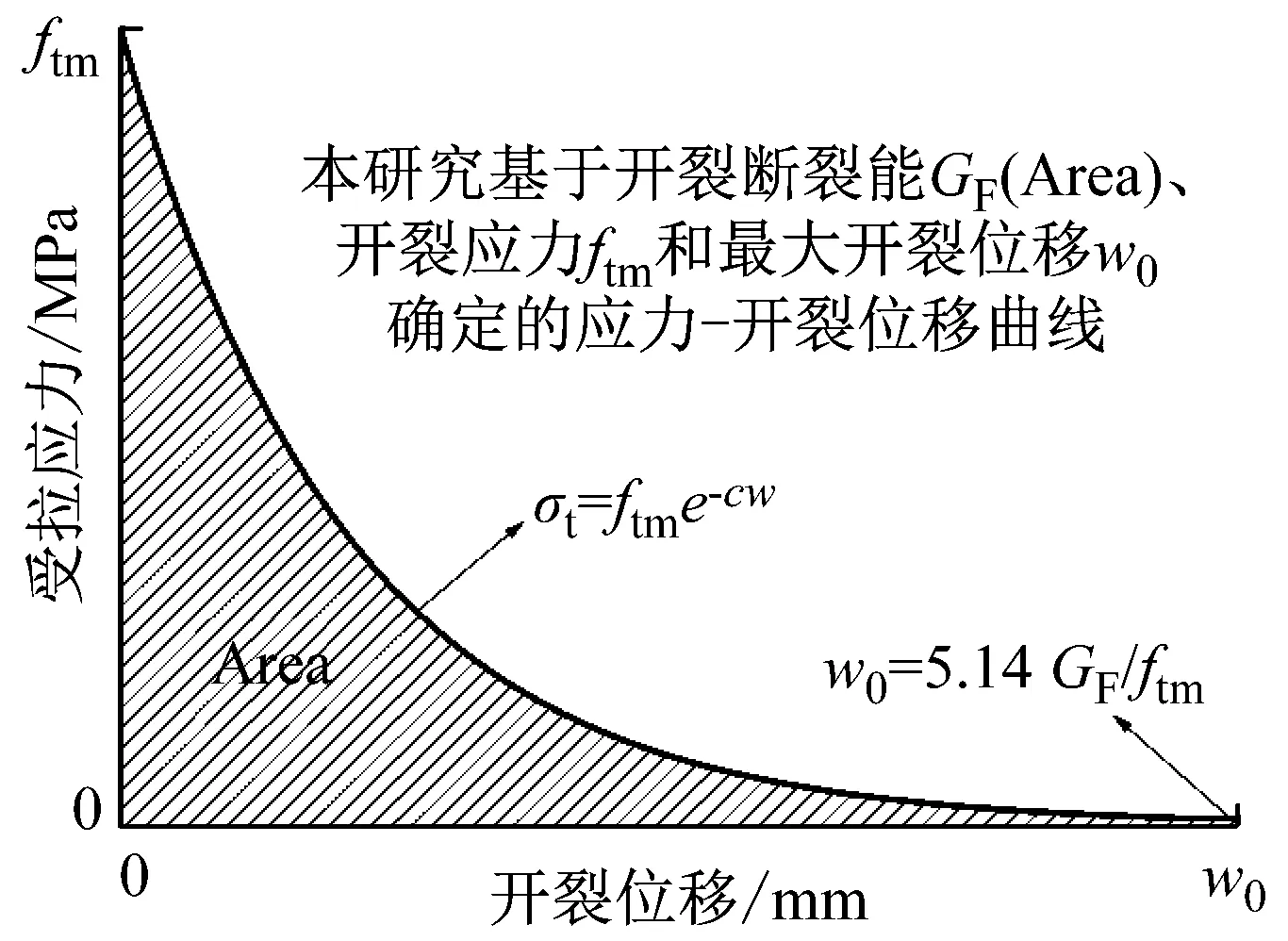
图3 应力-开裂位移曲线Fig.3 The stress-crack opening relationship
σt=ftme-cw
(12)
式中:w为开裂位移,单位mm;ftm为混凝土抗拉强度平均值,根据式(13a)计算,单位MPa;c为软化参数,与混凝土的强度等级有关。经数据拟合后,参数c按式(13b)确定。

(13a)
(13b)
如图3所示,软化应力-开裂位移曲线是根据开裂断裂能GF(曲线阴影面积Area)、开裂应力ftm和最大开裂位移w0这三参量确定的,能够反映混凝土受拉应力随着开裂位移的增加而逐渐退化(软化行为)和裂缝开展过程中的能量耗散等特征。此外,该应力-开裂位移曲线适用于强度在12~120 MPa下的混凝土材料。
根据Bazant等[24]提出的裂缝带理论,应力-开裂位移曲线可根据式(14)[25]转换成应力-开裂应变曲线。

(14)
混凝土的开裂断裂能GF根据式(15)计算,混凝土受压破碎断裂能Gc根据式(16)[26]确定。
GF=0.073(fcm)0.18
(15)
(16)
3 混凝土拉/压损伤参数评价与选用
由式(1a)~(1b)和式(4)~(5)可知,描述混凝土卸载时刚度弱化响应的损伤参数包括受拉dt、受压dc损伤参数。由于目前ABAQUS用户手册中没有指明损伤变量的具体计算方法,因此现将已有的几种损伤参数计算方法进行对比评价(表1),以期选择适用的损伤参数模型。

表1 损伤参数计算模型Tab.1 Calculation models of damage parameters
本研究以C30混凝土为例,采用上述5种计算模型确定的拉、压损伤参数曲线如图4所示。由图4(a)可知,应变等效模型[27]计算的受压损伤参数dc在所有曲线的最上方,损伤发展最为激烈。方自虎模型[10]下的受压损伤参数dc从峰值应力开始计算,没有考虑混凝土在强化阶段的受压损伤发展与累积。当非弹性应变小于0.005时,Birtel模型[11]与能量等效模型[28]计算的受压损伤参数dc比较接近;当非弹性应变超过0.005时,Birtel模型[11]计算的受压损伤参数dc比能量等效模型更大,说明损伤发展更快。从图4(b)可知,应变等效模型[27]和Birtel模型[11]计算的受拉损伤参数dt较接近且在所有曲线的最上方,损伤发展最为激烈。方自虎模型[10]计算的受拉损伤参数dt在所有曲线的最下方,损伤发展较慢,不能较好描述混凝土受拉时表现出来的脆性特性。能量等效模型[28]计算的受拉损伤参数dt介于其他3个模型之间,损伤发展偏缓慢。
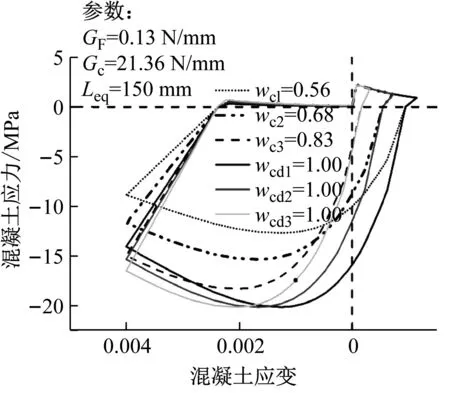
(a) θ=1

(a) 受压损伤
以上的对比的四种损伤计算模型,主要是基于混凝土材料而建立的。然而,对于RC结构分析,有必要考虑受力钢筋对混凝土损伤发展的影响,特别是对于受拉的情况。此外,ABAQUS用户手册还指出,对RC结构分析时应适当考虑钢筋与混凝土协同工作的“拉伸硬化”效应。考虑到直接建立针对RC结构的损伤计算模型难度较大,因此本研究暂未深入研究损伤计算模型,而是通过对比现有的损伤计算模型的发展形态,选择损伤随非弹性应变和开裂应变发展速度处于中间水平的Sidoroff能量等效模型作为基准模型,以此来计算RC结构中混凝土的受压dc、受拉dt损伤参数。
4 开裂-闭合受压刚度恢复因子wc计算模型
4.1 wc计算模型的建立
CDP模型中通过引入受拉wt、受压wc刚度恢复因子来描述混凝土在循环荷载下混凝土裂缝张开、闭合及裂缝之间的相互作用,以期更好模拟循环荷载下混凝土的反应。试验研究表明当混凝土从受压进入到受拉状态,若进入受拉前已有受压微裂缝形成时,应力反转时混凝土的受拉刚度不能恢复;当混凝土从受拉进入受压状态时,随着裂缝的闭合混凝土的受压刚度可以恢复。因此,在本文研究中,不考虑混凝土从受压进入受拉状态时的刚度恢复效果(wt=0为默认值),重点关注混凝土从受拉进入为受压状态时的刚度恢复程度(其中wc=1为默认值)。图5给出了混凝土从受拉进入到受压状态时受压刚度恢复因子wc的变化。
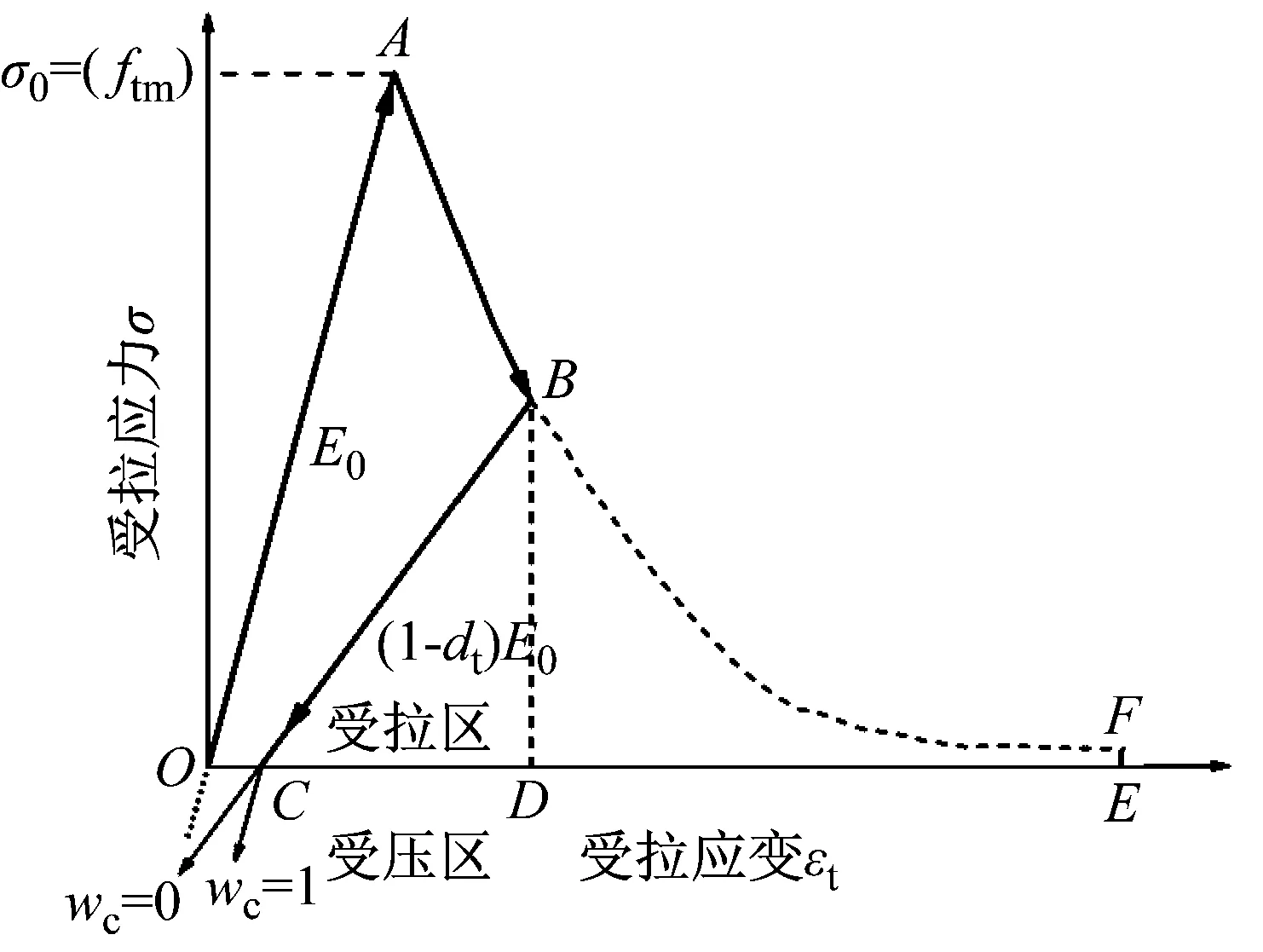
图5 受压刚度恢复因子wc的影响Fig.5 Effect of the compression stiffness recovery factor wc
关于图5中wc的变化讨论,本研究先假定混凝土在初始受拉时没有受压损伤(无受压塑性应变),有dc=0,代入式(5)和式(6b)得
(1-d)=(1-scdt)=
1-(1-wc(1-r*(σ11)))dt
(17)
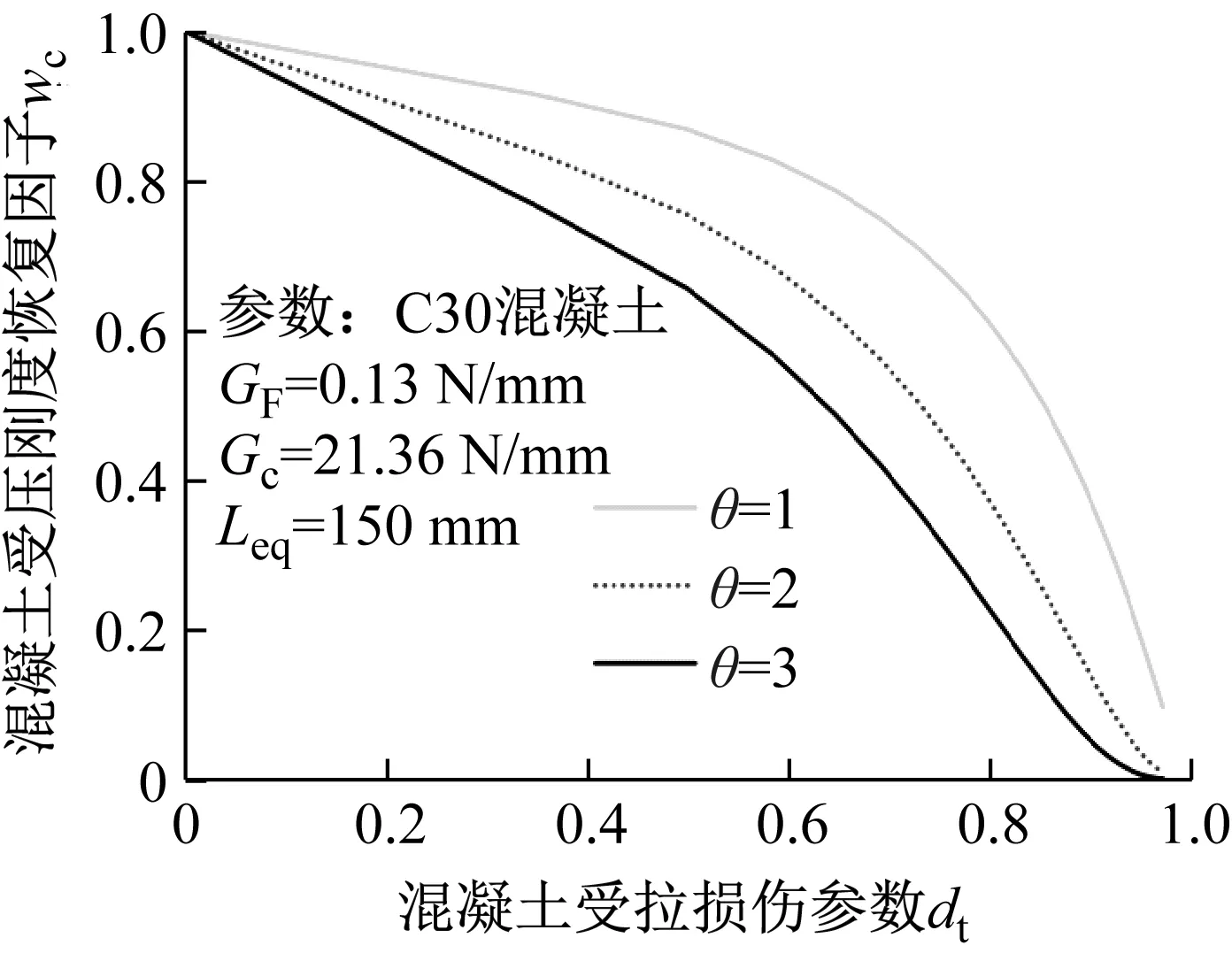
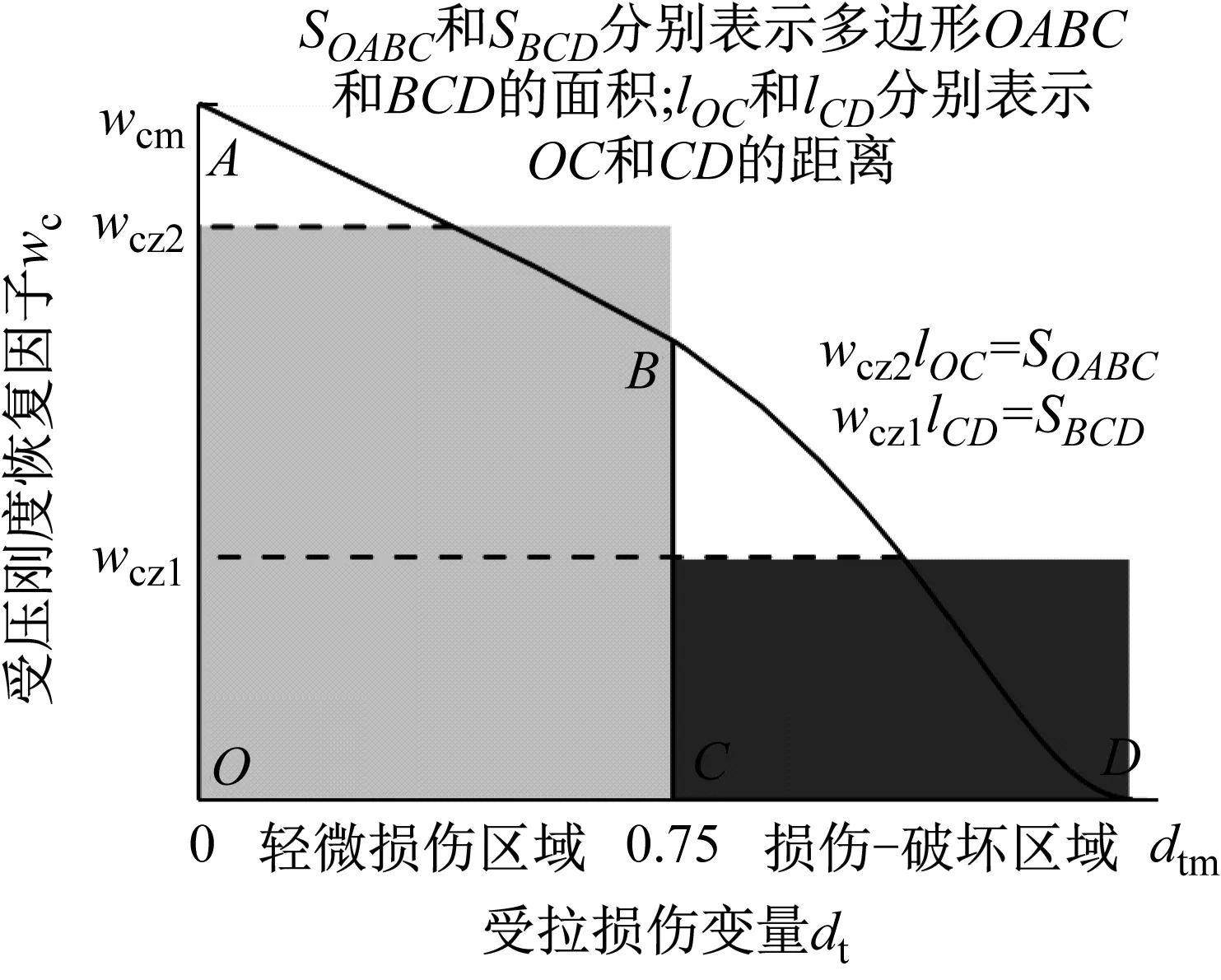
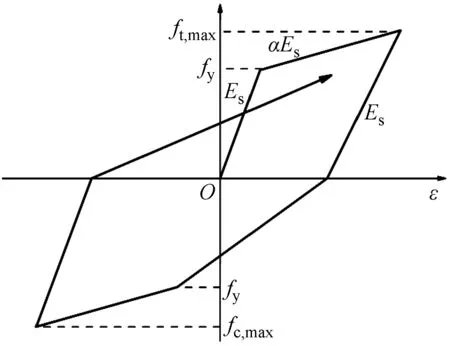
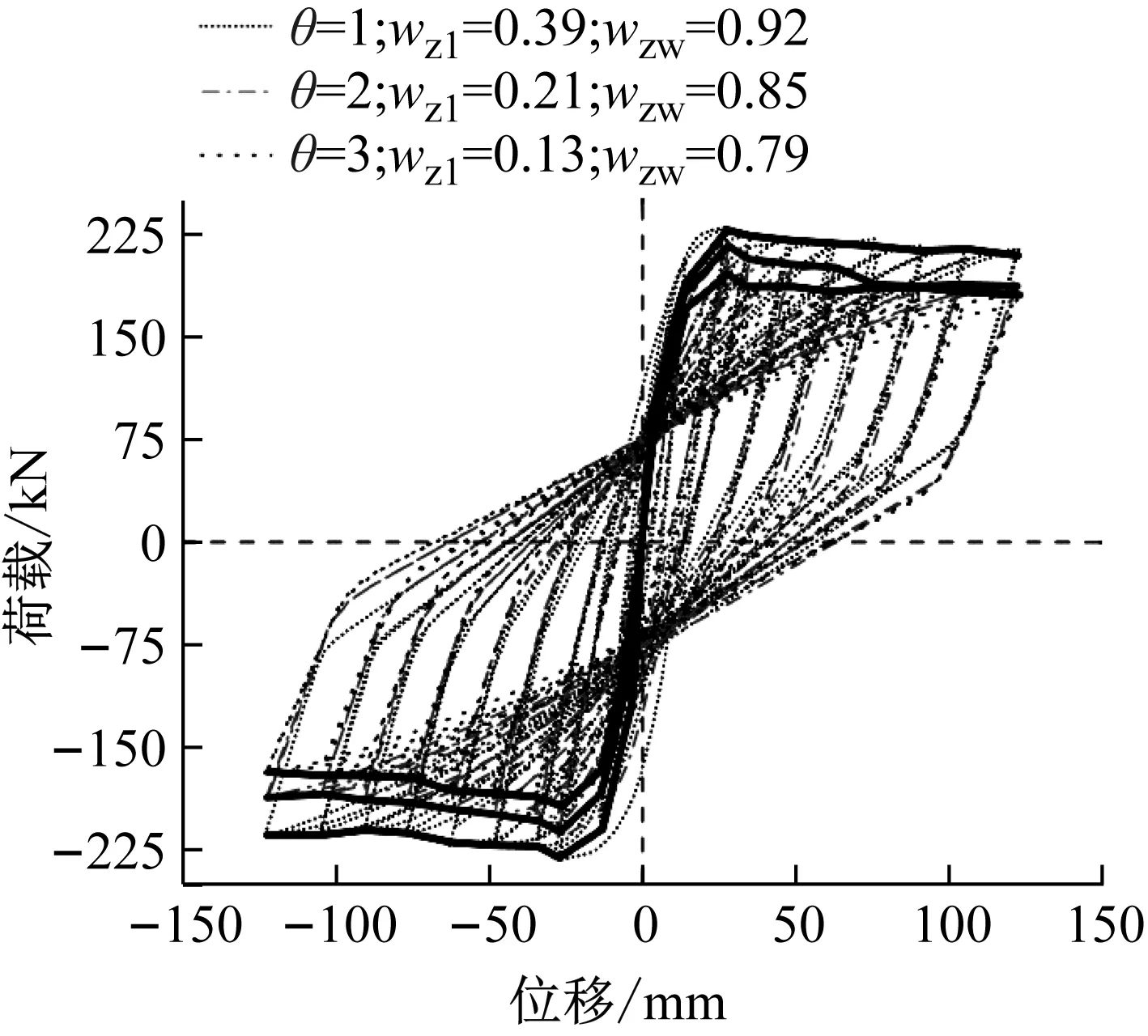
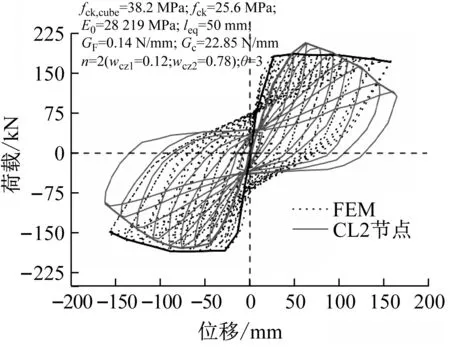
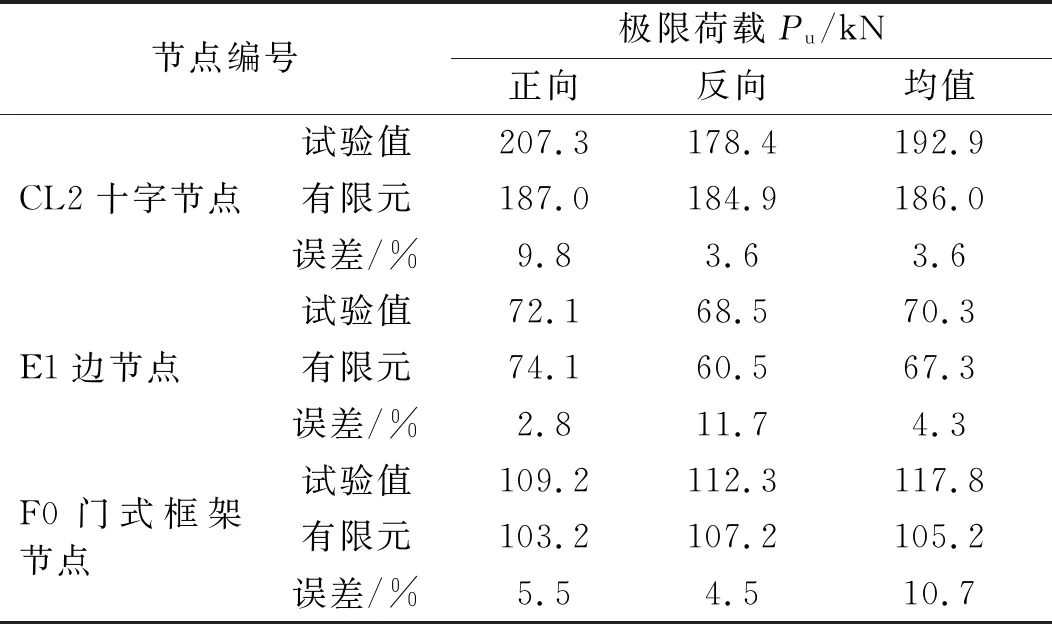
由式(17)知,当混凝土受拉(σ11>0)时,有r*(σ11)=1,因此d=dt。当混凝土受压(σ11<0)时,有r*(σ11)=0,因此d=(1-wc)dt。若wc=0,则d=dt,此时材料刚度没有恢复;wc=1,有d=0,材料完全恢复压缩刚度;0 为对比不同wc取值(0≤wc≤1)对混凝土刚度恢复程度和混凝土单元强度大小,本研究以几何尺寸为150 mm、强度为C30的立方体混凝土单元为例,分别模拟了混凝土相同dt下wc为0、0.5和1时混凝土单元从受拉进入为受压状态时的力学行为(图6)。 图6 相同dt下不同wc对混凝土“由拉进入压”后的力学行为影响Fig.6 Concrete compressive behaviour after cracking under the same dt with different wc values 由图6可知,随着wc取值增大,混凝土单元的弹性模量逐渐增大,单元的峰值强度也逐渐递增,并且混凝土单元在相同变形处卸载时材料的卸载响应也更加缓慢。wc=1时对应的弹性模量为26 209 MPa,分别是wc=0.5(15 722 MPa)和wc=0(5 211 MPa)的1.67倍和5.03倍。wc=1时对应的单元峰值强度为20.1 MPa,分别是wc=0.5(12.1 MPa)和wc=0(4.0 MPa)的1.67倍和5.03倍。可见,wc的取值会直接影响到混凝土单元的弹性模量与峰值强度。 综上可知,wc值影响混凝土的刚度恢复程度主要体现在弹性模量和峰值强度两方面。因此,为了准确预测循环荷载作用下RC结构的宏观承载力,有必要建立确定wc取值的计算模型,以期获得合理的wc值描述循环荷载下混凝土裂缝开裂后闭合行为后的刚度恢复效应。如图5所示,对于循环荷载下的混凝土,当受拉混凝土在软化段B点卸载时,可认为混凝土的微裂缝将沿着卸载路径B→C逐渐闭合。通常混凝土在拉→压过渡区存在一个刚度恢复过程,即受拉应力卸载至C点时微裂缝并不会完全闭合。为简便,本研究假设微裂纹在C点处完全闭合,并将多边形BCEF的面积视为一种材料性质,即裂缝完全闭合点(C点)处对应的受拉残存断裂能密度gFR。进一步地,本研究基于混凝土受拉应力-应变关系(图5),以受拉残存断裂能密度gFR与开裂断裂能密度gf比值的θ次方(θ为实数)建立了wc计算模型,其表示如下 (18) 式中:θ(θ≥1)为受压刚度恢复修正参数;gf为混凝土开裂断裂能密度(gf=GF/leq),单位N/mm2;s1与s2分别为三角形BCD与多边性BDEF区对应的面积(受拉残存断裂能密度),单位N/mm2;s1与s2根据式(19)进行计算。 s1= (19a) (19b) 式中:wt为B点对应的开裂位移,单位mm;dt为描述卸载支路(B→C)上的受拉损伤参数;c为式(13)中的软化参数。 以C30立方体混凝土单元为例,并选择能量等效模型[28]计算混凝土的受拉损伤参数dt。图7给出了wc计算模在不同θ取值下wc与dt的变化规律图。 图7 θ值对受拉损伤参数-受压刚度恢复因子wc的影响Fig.7 Effects of θ to the compressive stiffness recovery factor wc 如图7所示,wc与dt呈非线性递减关系;在相同dt数值下,wc数值会随着θ取值增大而减小。可见,θ会直接影响到wc-dt曲线的衰减速度。 同样以C30混凝土为例,模拟并对比了混凝土在不同dt下wc分别取默认值(wcd1/2/3=1)和本研究提议的计算值下的滞回行为(图8)。关于计算值选取如图7所示,以θ=1、3下的wc-dt曲线为基础,模拟了dt为0.58、0.75和0.83下混凝土卸载后再反向加载时刚度恢复效应。 以上工作中,已完成了循环荷载下混凝土开裂后闭合行为的wc计算模型的建立,并对其演化规律进行讨论。由于ABAQUS中CDP模型下的wc只支持某一常数定义,不能描述混凝土在不同dt下具有不同的刚度恢复效应。为解决这一问题,本研究选择循环荷载下严重破损的RC节点作为研究对象,基于现有混凝土裂缝特征与受拉损伤状态的统计关系,提出了一种基于拉伸损伤水平dt的模型简化处理方法。以0≤dt1≤0.75和0.75≤dt2≤dtm(dtm≤1)将RC节点简单划分为轻微损伤和损伤-破坏区两个区域,并分别采用特征受压刚度恢复因子wcz1和wcz2来定义两个区域的材料属性。轻微损伤和损伤-破坏区域范围分别采用构件的非塑性铰和塑性铰区域进行度量,采用由Paulay等[29]提议的塑性铰长度计算公式确定RC构件的塑性铰区域(式20)。 Lp=0.08L+0.022fyd (20) 式中:Lp为塑性铰长度;L为构件剪跨;d受拉钢筋直径,单位mm;fy为受拉钢筋强度,单位MPa。 受拉损伤参数dt的区间划分和不同区域的受压特征刚度恢复因子wcz1与wcz2的计算方法如图9所示,受拉损伤分区分为0≤dt≤0.75与0.75≤dt≤dtm(dtm≤1)两个区间,根据面积等效的原则计算每个区间对应的wcz1与wcz2,其中参数wcz1与wcz2分别用来定义图11(a)中对应的黑色与灰色区域。 图9 特征受压刚度恢复因子Fig.9 Characteristic value of the compressive stiffness recovery factor 以Yang等[30]研究中的CL1节点为研究对象,采用ABAQUS软件进行三维有限元建模分析。混凝土采用实体单元C3D8R模拟,钢筋采用桁架单元T3D2模拟,并采用Embedded命令将钢筋内置于混凝土单元内。混凝土采用CDP模型,钢筋选用由Clough提出的材料模型(图10)模拟[31-32],该模型通过削减钢筋的卸载刚度来替代RC结构中因钢筋与混凝土间的黏结滑移效而导致的强度退化和刚度退化。 图10 钢筋本构关系Fig.10 The reinforcement constitutive relationship CL1节点的几何尺寸和配筋详细见文献[30],混凝土150 mm立方体抗压强度fcu-150为35.5 MPa,纵向钢筋和横向钢筋的屈服强度分为528 MPa和407 MPa。根据试验的边界条件,将梁两端50mm区段采用刚体约束,并指定刚体的转动中心为梁端面的形心位置处;柱子底部采用固定铰约束;柱顶先施加竖直向下的轴压荷载(1 420 kN),然后在柱顶面施加平行于梁轴线方向的水平循环位移荷载,循环加载制度如图11所示,每级加载位移循环2次。采用ABAQUS/Standard模块中的Newton-Raphson算法求解,通过增量步施加荷载,经过若干次平衡迭代逐步获得解答。有限元元模型边界和网格如图12所示。 图11 CL1节点加载制度Fig.11 Loading system for CL1 joint (a) 混凝土 如4.2节所述,对一个确定的有限元模型,受压刚度恢复修正参数θ是一个确定的常量。从wc-dt曲线中可以看出θ的取值会直接影响到wc-dt曲线的衰减速度。因此,本研究将参数θ作为参数变量进行数值模拟研究,并分别取θ等于1、2和3时进行数值计算,通过对比有限元的模拟结果来标定θ的取值范围,以期得到较好的模拟结果。CL1节点在不同θ取值下模拟结果见图13和图14。 图13 不同θ取值下的模拟结果对比Fig.13 Comparison of the FE results with the different values of θ (a) θ=2 由图13可知,当θ增大时RC节点的峰值承载力降低,整个滞回环的面积减小,节点的耗能能力降低。相反地,θ太小可能会高估RC节点的承载力和耗能能力。当θ取2或3时,模拟结果在峰值承载力和滞回环面积方面相差较小,说明数值模拟结果趋于稳定。经有限元分析发现,当θ≥3时,混凝土wc-dt曲线衰减加快,从而导致wc1和wc2过小,这会使得模拟结果严重低估结构的承载力甚至导致有限元模型分析不收敛。可见,θ取值应该控制在1~3之间(1≤θ≤3)比较合理。 如图14所示,通过对比θ=2(或3)下的模拟结果与试验结果发现,当θ=3时的模拟结果更加逼近试验结果。因此,对于循环荷载下RC节点,θ=3可作为确定wc计算模型的默认值。 基于以上循环荷载下混凝土开裂闭合行为相关演化算法,包括受压刚度恢复因子wc演化规律的合理性和简化有限元计算方法的可行性,进一步对其他类型框架十字节点CL2、边节点E1[33]和门式闭合节点F0[34]作为算例进行有限元建模分析,有限元模型的单元类型与材料模型的选择、算法控制与CL1节点模型保持一致,模拟结果见图15。 (a) 十字节点CL2 通过骨架曲线,可以得到RC节点的极限荷载,有限元结果与试验结果对比如表2。 表2 不同RC节点的极限荷载对比Tab.2 Comparison of the ultimate loads for the different type of the RC joints 由表2可知,有限元计算的极限承载力普遍小于试验值,误差在2.8%~11.7%。综合考虑模拟骨架曲线与试验骨架曲线的整体变化趋势以及承载力误差范围,有限元模型均能较好的反映结构的实际力学响应。由此可见,本文建立的wc演化算法和循环荷载下简化有限元计算方法的可行性,也验证了θ=3时能获得较好的模拟结果。 (1) 本研究基于混凝土开裂断裂能GF提出了适用于混凝土非线性分析的指数型软化段应力-开裂位移曲线,该曲线是根据GF、开裂应力ftm和最大开裂位移w0这三参量确定的,能够反映混凝土受拉应力随着开裂位移的增加而逐渐退化(软化行为)和裂缝开展过程中的能量耗散等特征。此外,该应力-开裂位移曲线适用于强度在12~120 MPa下的混凝土材料。 (2) 通过对比评价现有的混凝土拉dt、压损伤参数dc计算模型,选择了适用于RC结构分析的能量等效dt和dc计算模型。 (3) 基于混凝土软化应力-应变关系建立了受拉残存断裂能密度gFR与开裂断裂能密度gf比值的θ次方(θ为实数)的wc计算模型,该计算模型同时考虑了单元特征长度leq和dt对变量wc的影响,同时本文还讨论了wc计算模型的演化规律和受压刚度恢复修正参数θ的取值。 (4) 基于现有混凝土裂缝特征与受拉损伤状态的统计关系,提出了一种基于拉伸损伤水平dt的模型简化处理方法。以0≤dt1≤0.75和0.75≤dt2≤dtm(dtm≤1)将循环荷载下严重破损的RC节点简单划分为轻微损伤(非塑性铰区)和损伤-破坏(塑性铰区)两个区域,分别采用特征受压刚度恢复因子wcz1和wcz2来定义两个区域的材料属性。采用ABAQUS对CL1节点进行建模分析,讨论了受压刚度恢复修正参数θ的取值(1≤θ≤3)。经过分析讨论后以θ=3可作为确定wc计算模型的默认值。 (5) 通过对循环荷载下的十字节点、边节点和门式框架RC节点进行数值模拟并与试验数据比较,有限元计算的极限承载力与试验值的误差在2.8%~11.7%,综合考虑模拟骨架曲线与试验骨架曲线的整体变化趋势以及承载力误差范围,有限元模型均能较好的反映结构的实际力学响应,验证了循环荷载下混凝土开裂-闭合行为计算方法的正确性以及有限元模型简化处理方法的可行性。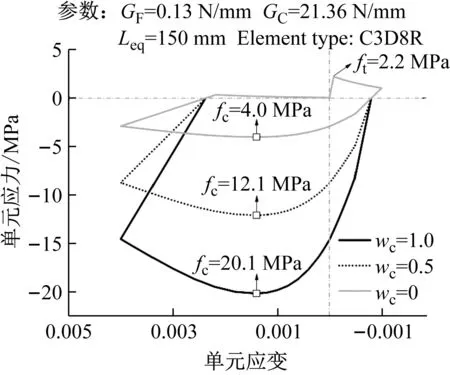
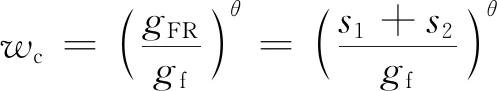
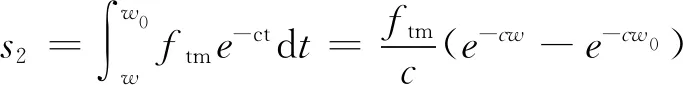
4.2 wc计算模型的演化规律讨论
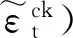
4.3 wc计算模型在RC节点模型中的应用
5 循环荷载下RC节点的数值模拟应用研究
5.1 有限元模型


5.2 受压刚度恢复修正参数θ取值讨论

5.3 循环荷载下不同RC节点数值模拟
6 结 论
