一种基于压缩感知的三维导体目标电磁散射问题的快速求解方法

丁亚辉 孙玉发 朱金玉

(安徽大学电子信息工程学院,合肥 230601)

1 引 言

矩量法[1−3]是求解导体目标电磁散射问题的常用方法,具有计算精度高、所用格林函数自动满足辐射条件、无须额外设置边界条件等优点.但是矩量法在求解电大尺寸问题时,会因为基函数个数过多、矩阵方程求解的复杂度过大导致计算时间难以接受.为此,有学者提出将压缩感知[4−6](compressed sensing,CS)引入矩量法.一种方法是通过引入稀疏变换矩阵实现对未知电流的稀疏表示,从而在压缩感知理论框架下构造欠定方程,并优化求解[7,8].这种方法已应用到旋转对称目标[9]和小波矩量法[10]中.另一种方法是首先构建富含空间信息的激励源,然后应用矩量法计算得到表面感应电流的观测值,进而可通过恢复算法获得宽角度目标表面感应电流[11−13].本文只讨论第一种方法,即构造欠定方程的方法.此方法只能用于二维或二维半的物体上,对三维问题效果不佳,原因是三维目标通过软件离散化建模,场源非有序分布,导致目标表面电流在常用的稀疏基上不稀疏.而一般获取稀疏基的字典训练算法又因为没有训练集无法应用在此方法上.

本文对上述方法加以改进,引入特征基函数[14−16]作为稀疏基,压缩感知恢复算法采用广义正交匹配追踪算法(GOMP)[17],并计算了三维导体目标的雷达散射截面(RCS),数值结果证明了该方法的准确性与高效性.

2 基本原理

2.1 压缩感知构造欠定方程

为了提高矩量法的计算效率,引入信号处理领域中压缩感知理论来降低内存需求,减少电流求解时间.

在求解目标表面电流时,将阻抗矩阵视为测量矩阵,待求解的表面电流视为要重构的信号,激励电压视为测量值.如果阻抗矩阵满足约束等距特性[18],便可以从测量值恢复出原始信号.而压缩感知中恢复算法只需用到低维的测量值,所以在应用中降低了电流求解时间.

根据矩量法,可得到矩阵方程

式中Z,J,V分别是阻抗矩阵、电流向量和激励向量,N是未知量的数目.通过对阻抗矩阵随机抽取M行构造欠定方程

通过应用稀疏变换矩阵Ψ使信号J在变换域上是稀疏的,即

A是信号J在Ψ上的变换向量,其稀疏度为K.则(2)式可表示为

其中,再用恢复算法恢复出电流.本文采用GOMP方法作为恢复算法.与正交匹配追踪(OMP)相比,GOMP在选择原子时每次选择最大的S个(本文取S=K/4),而OMP只选择一个,所以GOMP与OMP精度相同,但速度更快.

CS方法需要事先知道目标表面电流的稀疏基,对于二维导体目标,由于目标表面电流的变化缓慢,所以可以使用离散余弦变化基.而三维导体目标表面划分为Rao-Wilton-Glisson(RWG)基函数,其目标表面电流在一般的正交基下不稀疏,使得CS方法的应用受到了限制.

2.2 特征基函数作为稀疏基

特征基函数法(CBFM)是一种基于区域分解的方法.特征基函数法首先将目标划分为若干个子域,在每个子域上构造主要特征基函数,并通过次要特征基函数来反映子域之间的相互作用,以此来实现矩阵方程的降阶,更适合后续直接法求解.本文需要用到主要特征基函数和次要特征基函数作为稀疏基,得到稀疏基后就可以准确地恢复出目标表面电流.

特征基函数法首先将目标划分成m个子域,如图1所示.为了保证人工划分子域边界电流的连续性,需要对每个子域进行扩展.图中虚线表示的是扩展子域边界,实线表示的是原始子域边界,子域扩展宽度取为λ/10—λ/8.

图1 目标子域划分示例Fig.1.Example of target subdomain partition.

当求解主要特征基函数(PCBFs)时,不考虑子域与子域之间的互耦作用,将每一个扩展子域看作独立子域来处理,分别计算其在对应入射波激励下的响应,于是有

式中Vi是扩展子域的对应入射波激励;是扩展子域i的自阻抗矩阵,维数是Ni×Ni,Ni是扩展子域i包含的RWG基函数个数.扩展子域PCBFs去除其扩展部分就可以得到原始子域的PCBFs.

当求解扩展子域的次要特征基函数(SCBFs)时,需要分别考虑扩展子域i与其他m−1个原始子域之间的互耦作用,即

当扩展子域i与原始子域j之间不重合时,阻抗矩阵Zij是扩展子域i与原始子域j之间的互阻抗,维数是Ni×Nj;当扩展子域i与原始子域j之间有重合时,阻抗矩阵Zij是扩展子域i与去掉重合部分的原始子域j之间的互阻抗,维数是Ni×(Nj−Nij),Nij是重合部分的RWG基函数个数.扩展子域SCBFs去除扩展部分即可得其原始子域SCBFs.

在求得CBFs后,目标表面电流可以表示为

式中,是第i个子域的特征基函数,是此特征基函数的加权系数.用矩阵可表示为

简写为

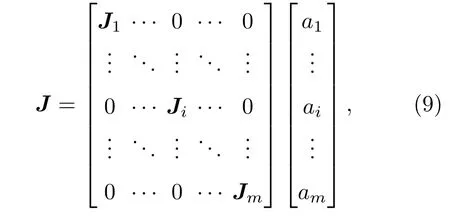
即

Jr就是压缩感知中所需要的稀疏基,a是目标表面电流在稀疏基上的稀疏表示.在求得稀疏基后,随机抽取M行阻抗矩阵ZM×N和其对应的激励VM×1,就可以用恢复算法准确地恢复出目标表面电流了.

需要指出的是该方法在划分子域时,要综合考虑特征基函数和恢复算法的复杂程度.如果目标划分的子域数量m过多,虽然每个子域所含未知数很少,便于求解PCBFs以及SCBFs,但是压缩感知稀疏度K却会增大,给恢复算法带来困难;如果目标划分子域的数量m过少,则每个子域所含未知数就会增多,CBFs生成效率会降低.在分析过程中应结合实际需求平衡m与计算效率之间的关系.在本文的算例中,压缩感知中的N为未知量数目,M取为N/2,K则根据文献[17]选择恢复概率大于90%的取值.m的取值要根据目标的大小、形状等综合考虑,取在附近.

3 数值算例与结果

为了验证本文方法的有效性,分别对导体球、组合导体目标和导弹模型的RCS进行了计算.所有算例均在Intel(R)Core(TM)i7-3820 CPU@3.60 GHz,56 GB RAM的PC机上完成,算例均采用双精度浮点运算.

算例1计算了导体球的双站RCS,导体球的半径为1.5 m,入射波频率为300 MHz,用三角单元剖分,共10970个三角形,未知量数目为16455,子域划分为27个,相邻子域扩展大小为1.2倍公共边平均长度,扩展后未知量数目为23253.图2给出了三种方法得到的双站RCS,由图可见压缩感知方法与中位数倍数(MOM)计算结果符合良好.三种算法的电流计算时间和误差列于表1,可见CS比CBFM计算时间减少,且精度更高.本文用相对均方根误差函数表示恢复误差,即

图2 导体球双站RCSFig.2.Bistatic RCS of conducting sphere.

表1 导体球电流计算时间Table 1.Comparison of computation time.

算例2讨论了三种方法在不同未知量数目时的双站RCS的计算时间,本算例的目标为半径1 m的导体球,入射波频率和剖分的未知量数目如表2所列,图3给出了三种方法的计算时间与未知量数目的关系.由图3可见,随着未知量数目的增加,压缩感知方法所用时间增长得更缓慢.

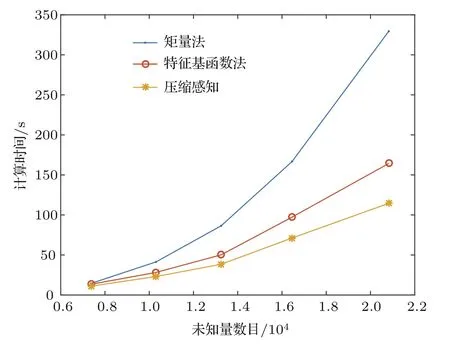
图3 导体球电流计算时间Fig.3.Computation time of current of conducting sphere.

算例3计算了九个组合导体目标的双站RCS,其中导体球的半径为0.5 m,导体圆锥半径为0.5 m,高为1 m,导体圆柱的半径为0.5 m,高为1 m,正方体边长为1 m,各导体底面中心相距1.5 m.入射波频率为300 MHz,用三角单元剖分,共16840个三角形,未知量数目为25260,子域划分为50个,相邻子域扩展大小为1.2倍公共边平均长度,扩展后未知量数目为40956.图4给出了三种方法得到的双站RCS,三种算法的计算时间和恢复误差如表3所列,可见CS比CBFM计算时间减少,且精度明显提高.

表2 不同入射波频率下的未知量数目Table 2.Number of unknown variable of different frequency.

图4 组合导体目标双站RCSFig.4.Bistatic RCS of composite conductor target.

表3 组合导体目标电流计算时间比较Table 3.Comparison of computation time.

算例4 计算了导弹模型的双站RCS,其中导弹模型的长为1 m,宽为0.64 m,高为0.22 m.入射波频率为1 GHz,用三角单元剖分,共10502个三角形,未知量数目为15753,子域划分为28个,相邻子域扩展大小为1.2倍公共边平均长度,扩展后未知量数目为24078.图5给出了三种方法得到的双站RCS,三种算法的计算时间和恢复误差如表4所列.

图5 导弹模型双站RCSFig.5.Bistatic RCS of simple missile model.

表4 导弹模型电流计算时间比较Table 4.Comparison of computation time.

4 结 论

本文改进了压缩感知和矩量法结合构造欠定方程的方法,引入特征基函数作为稀疏基,恢复算法采用广义正交匹配追踪算法.应用改进方法计算三维导体目标的RCS,数值计算结果表明,本文方法在保证精度的同时,计算效率也得以提高.

本文虽然提高了目标RCS的计算效率,但是在计算特征基函数时,仍然需要填充稠密的阻抗矩阵.所以,快速获得特征基函数(即稀疏基)可以进一步提高计算效率.压缩感知理论的新进展——结构化压缩感知[19,20],可以将与数据采集硬件及复杂信号模型相匹配的先验信息引入传统压缩感知,从而实现对更广泛类型的信号准确有效的重建.我们今后会进一步研究,将结构化压缩感知应用到本文工作中.

[1]Gibson W C 2014J.Electromagn.Waves Appl.1 181

[2]Andriulli F P,Cools K,Bagci H,Olyslager F,Buffa A,Christiansen S,Michelssen E 2012IEEE Trans.Antennas Propag.56 2398

[3]Chen Y,Zuo S,Zhang Y,Zhao X,Zhang H 2017IEEE Trans.Antennas Propag.65 3782

[4]Candè E J,Wakin M B 2008IEEE Signal Process.Mag.25 21

[5]Ji S,Xue Y,Carin L 2008IEEE Trans.Signal Process.65 3782

[6]Ender J H G 2010IEEE Trans.Signal Process.65 3782

[7]Wang Z,Wang B Z 2014Acta Phys.Sci.63 120202(in Chinese)[王哲,王秉中 2014物理学报 63 120202]

[8]Chai S R,Guo L X,Li J,Li K 2015Asia-Pacific Microwave ConferenceNanjing,China Dec.6–9,2015 p1

[9]Kong M,Chen M S,Wu B,Wu X 2017IEEE Antennas Wirel.Propag.Lett.1 99

[10]Wang Z,Wang B Z,Wen Y Q,Wang R 2015IEEE International Symposium on Antennas and Propagation&Usnc/ursi National Radio Science MeetingVancouver,BC,July 19–24,2015 p1488

[11]Chao X Y,Chen M S,Wu X L,Shen J 2013Chin.J.Electron.41 2361(in Chinese)[曹欣远,陈明生,吴先良,沈晶2013电子学报41 2361]

[12]Du H M,Chen M S,Wu X L 2012International Conference on Microwave and Millimeter Wave TechnologyShenzhen,China May 5–8,2012 p1

[13]Chai S R,Guo L X 2015Acta Phys.Sin.64 060301(in Chinese)[柴水荣,郭立新 2015物理学报 64 060301]

[14]Prakash V V S,Mittra R 2003Microw.Opt.Technol.Lett.36 95

[15]Sun Y F,Chan C H,Mittra R,Tsang L 2003Antennas and Propagation Society International SymposiumColumbus,OH,USA June 22–27,2003 p1068

[16]Wang Z G 2014Ph.D.Dissertation(Hefei:Anhui University)(in Chinese)[王仲根 2014博士学位论文(合肥:安徽大学)]

[17]Jian W,Kwon S,Shim B 2012IEEE Trans.Signal Process.60 6202

[18]Tropp J A,Gilbert A C 2007IEEE Trans.Inf.Theory53 4665

[19]Baraniuk R G,Cevher V,Duarte M F,Hegde C 2010IEEE Trans.Inf.Theory56 1982

[20]Duarte M F,Eldar Y C 2011IEEE Trans.Signal Process.59 4053