梯度弹性多孔材料吸声性能分析与优化设计

2021-05-17马文婷郝耀东梁鸿宇黄晓迪马芳武

振动与冲击 2021年9期

陈鑫，马文婷，郝耀东，梁鸿宇，黄晓迪，马芳武

(1.吉林大学汽车仿真与控制国家重点实验室,长春 130022；2.中国汽车技术研究中心有限公司,天津 300300)

多孔材料具有良好的吸隔声性能，广泛应用于汽车声学包上，从而保证整车NVH性能。多孔材料按骨架类型可分为三类：刚性、柔性、弹性。金属泡沫多用刚性骨架多孔材料模型，软纤维层多用柔性骨架多孔材料模型，聚合物泡沫多用弹性骨架多孔材料模型[1-2]。

为了提高多孔材料的吸声性能，对梯度多孔材料的研究逐渐增多。刘新金等[3]通过合理配置分层材料的结构参数得到了较好的宽频吸声系数。王永华等[4]通过研究仿生耦合模型，提高了多孔材料的全频吸声性能。敖庆波等[5-6]通过在纤维多孔材料中应用梯度孔隙率结构，获得了更好的宽频吸声性能且峰值谷值之差较小。Zhu等[7]通过实验方法研究了梯度孔结构对金属纤维多孔材料吸声性能的影响，有效改善了吸声性能，孔梯度界面的方向和数量对吸声性能有显著影响。敖庆波等[8]通过研究孔隙率梯度和丝径梯度结构，认为当材料总厚度不同时，梯度排列顺序对吸声性能的影响规律不同。Wang等[9]通过研究3 mm以下厚度的金属纤维多孔材料的吸声性能，认为吸声系数受层间界面的影响较大。

目前，对梯度多孔材料的研究表明其可以有效改善多孔材料的吸声性能，但是以上研究主要针对于刚性多孔材料，而对于对梯度弹性多孔材料的研究较少，并且缺少对梯度结构厚度分布的研究。本文首先采用Biot理论及传递矩阵法推导了多层弹性多孔材料的吸声系数理论模型，并采用阻抗管法验证了理论模型的准确性。以聚氨酯泡沫为例，通过数值计算的方法研究了四种梯度孔隙率结构以及梯度差对弹性多孔材料吸声性能的影响，同时利用多岛遗传算法对层厚进行优化设计，得出最优设计方案。

1 理论模型

弹性多孔材料由固相和流相组成，在介质中存在三种同时传播的声波：弹性压缩波、弹性剪切波以及声波压缩波。基于Biot理论，弹性多孔材料的体积模量和有效密度的表达式为[10]

(1)

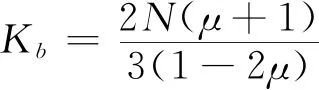
(2)

(3)

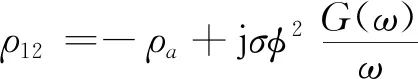
(4)

(5)

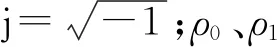
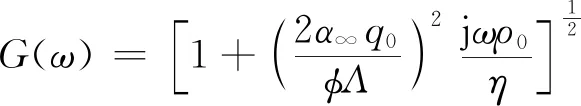
(6)

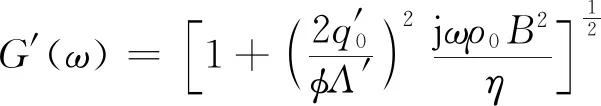
(7)

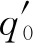
图1 平面波入射背靠刚性墙的多层弹性多孔材料Fig.1 Plane wave incident multilayer elastic porous material against rigid wall

设M1和M2为分别为某一层多孔材料前后表面上的点，则有关系式[11]

Vp(M1)=[Tp]Vp(M2)

(8)

式中，[Tp]为弹性多孔材料的传递矩阵，其表达式如下

[Tp]=[T(0)][T(d)]-1

(9)

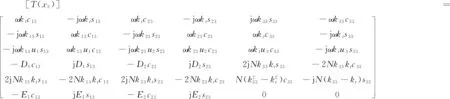
(10)

式中:d为厚度；u1、u2和u3分别为两个压缩波的空气和骨架的速度之比以及剪切波的空气和骨架的位移幅值之比；kt为声波在x1方向的分量；k13、k23和k33分别为三种声波在x3方向的分量；Di和Ei为参数；ci3=cos(ki3x3)，i=1,2,3；si3=sin(ki3x3)，i=1,2,3，其中：

(11)

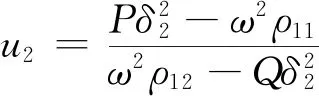
(12)

(13)

(14)

(15)

式中:δ1、δ2和δ3分别为弹性压缩波、声波压缩波和弹性剪切波的波数；P、Q和R为弹性系数。

弹性多孔材料分别与弹性多孔材料、空气以及刚性墙之间的声场关系为

[I]V(M2)+[J]V(M3)=0

(16)

[If1]V(A)+[Jf1]V(M)=0

(17)

[Yp]V(M2n)=0

(18)

式中:[I]和[J]为相邻两层多孔材料之间的耦合矩阵；[If1]和[Jf1]为空气与多孔材料之间的耦合矩阵；[Yp]为弹性多孔材料与刚性墙之间的关系矩阵。

计算表面阻抗的总矩阵[D]为

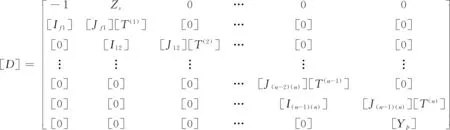
(19)

表面阻抗Zs的表达式为

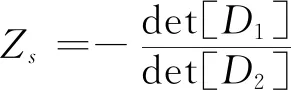
(20)

式中，[D1]和[D2]分别为去掉[D]的第一列和第二列后的矩阵。

扩散声场下，弹性多孔材料的吸声系数αd的计算公式为

(21)

式中:α为吸声系数；θ为声波入射角度。

2 试验验证

2.1 样件制备

为了验证理论模型的准确性，取吸音棉和聚氨酯泡沫两种材料，每种材料分别切割成直径为100 mm和29 mm的试验样件，如图2所示。采用驻波管法测量吸音棉、聚氨酯泡沫以及聚氨酯泡沫-吸音棉组合结构的吸声系数，选用直径分别为100 mm和29 mm的阻抗管，如图3所示。直径为100 mm的阻抗管的测试频率范围为100～1 600 Hz，直径为29 mm的阻抗管的测试频率范围为500～6 400 Hz。其中，吸音棉和聚氨酯泡沫的厚度均为0.023 m。这两种材料的声学参数如表1所示。

(a) 吸音棉试验样件

图3 驻波管Fig.3 Standing wave tube

表1 吸音棉与聚氨酯泡沫参数Tab.1 Parameters of sound-absorbing cotton and polyurethane foam

2.2 结果与讨论

将通过驻波管法测得的吸音棉、聚氨酯泡沫以及聚氨酯泡沫-吸音棉组合结构的吸声系数曲线与通过理论模型计算得到的吸声系数曲线进行对比，如图4所示。

从图4可以看出，对于单层材料，由驻波管试验测量得到的吸声性能曲线与理论值基本吻合。对于双层材料，试验测得的吸声性能曲线与理论值稍有差别，这可能是由于两层材料接触处不严密，存在不均匀的空气层所造成的。通过对比由驻波管试验测量和理论模型计算得到的吸声系数曲线，可以验证本文理论模型的准确性和可靠性。

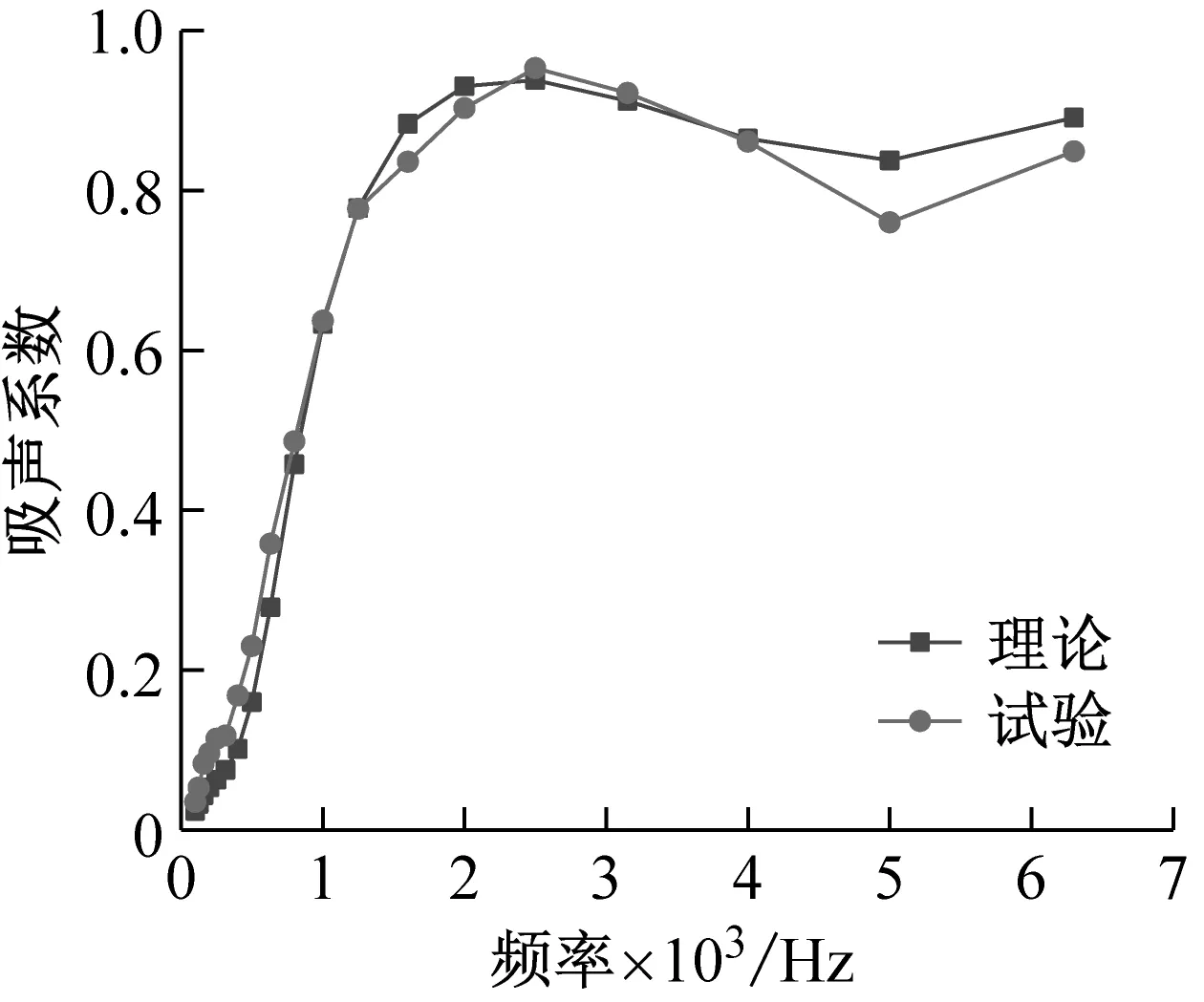
(a) 吸音棉

3 梯度弹性多孔材料吸声性能分析

3.1 不同梯度结构对吸声系数的影响

对于梯度弹性多孔材料，材料分为若干层，声波进入每一层都会产生透射声波和反射声波，相较于单一孔隙率结构有更为复杂的声波传递路径及更多的能量损失。为了研究梯度弹性多孔材料的吸声性能，本文采用聚氨酯泡沫进行声学性能分析。聚氨酯泡沫的声学参数如表2所示。

表2 聚氨酯泡沫参数Tab.2 Polyurethane foam parameters

分别取孔隙率为0.96、0.86、0.76、0.66、0.56、0.46、0.36、0.26、0.16，厚度均为0.03 m，其余参数不变的聚氨酯泡沫，计算其100-10 000 Hz频率段内的吸声系数，计算结果曲线如图5所示。

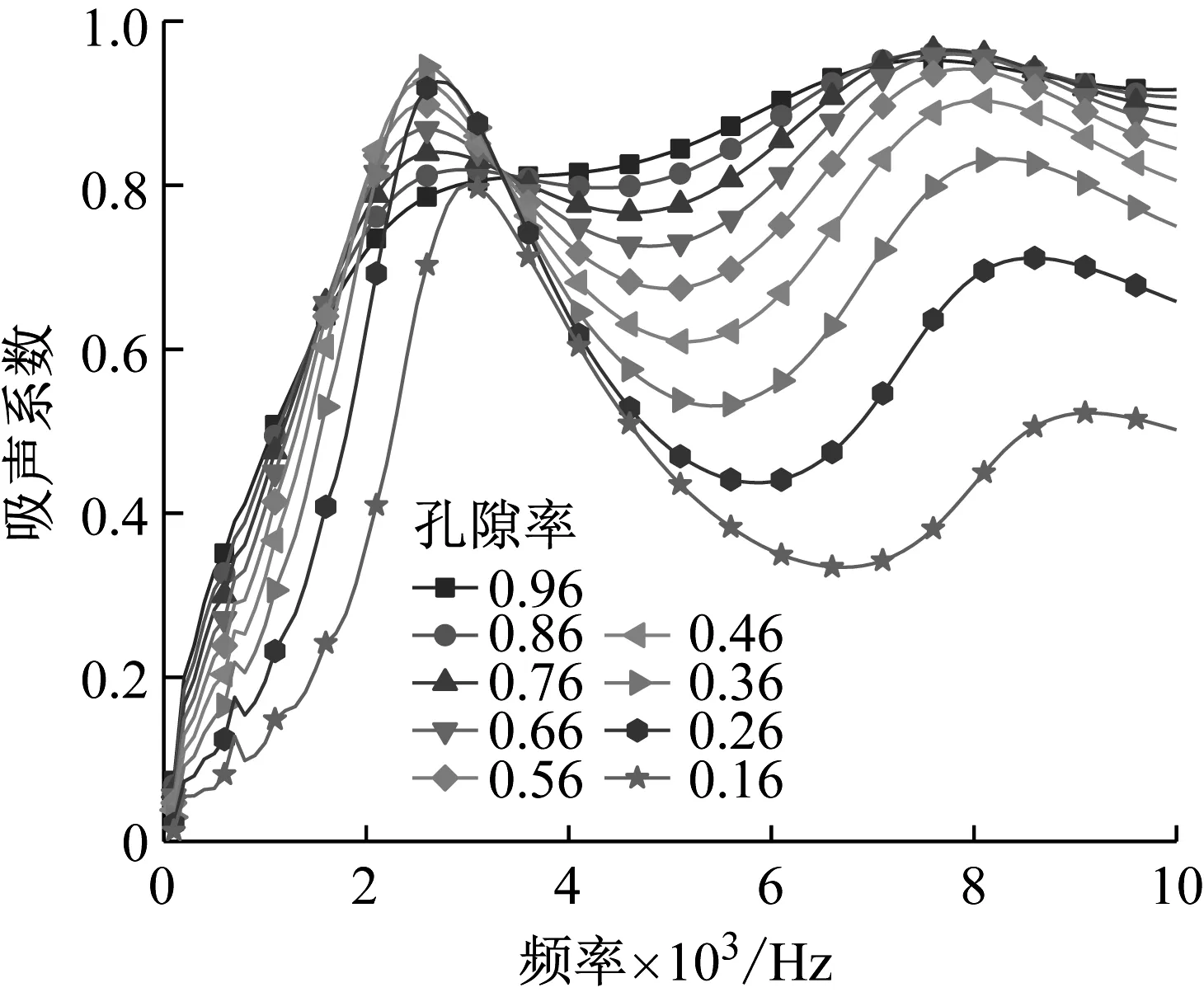
图5 孔隙率对吸声系数的影响Fig.5 Effect of porosity on sound absorption coefficient

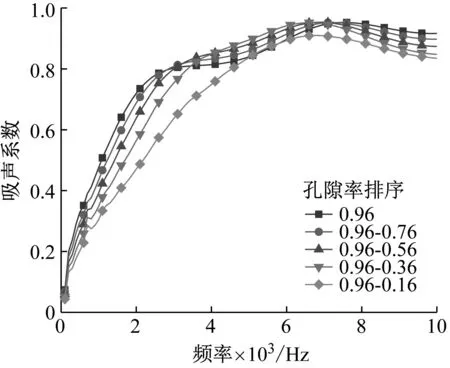
从图5可以看出，当孔隙率由0.96减小到0.36时，第一峰值逐渐增大，当孔隙率减小到0.26以下时，第一峰值随孔隙率的减小而大幅度减小。当频率为3 500 Hz以上时，吸声系数随孔隙率的减小呈下降趋势。当孔隙率为0.36时，第一峰值达到最大，为0.94，当孔隙率为0.76时，第二峰值达到最大，为0.96。对于弹性多孔材料，随着孔隙率的减小，吸声系数-频率曲线整体向右移动，存在使第一峰值最大的最佳孔隙率。

本文主要研究四种常见的梯度孔隙率结构，如表3所示。取较高孔隙率为0.96，较低孔隙率为0.36。对于双层结构，各层材料厚度均为0.015 m，对于三层结构，各层材料厚度为0.01 m，总厚度均为0.03 m。图6为四种梯度孔隙率结构对吸声系数的影响。

表3 结构方案Tab.3 Structural scheme

从图6可以看出，相比于孔隙率为0.96的单层结构，方案一在3 500-7 000 Hz频段内的吸声系数较高，其他频率的吸声系数较差，整体曲线趋势与孔隙率为0.96的单层结构较为接近。相比于孔隙率为0.36的单层结构，方案二在800-2 100 Hz频段内的吸声系数较高，最大吸声系数差值可达0.455，但其他频率的吸声系数较差，整体曲线趋势与孔隙率为0.36的单层结构较为接近。三层结构相较于单层结构都可在1 000-3 000 Hz频段内获得较高的吸声系数，但在高频处的吸声系数较差，方案三的宽频吸声系数要好于方案四。由此可知，方案一的吸声系数峰值主要与较大孔隙率单层结构的峰值有关，方案二、三、四的吸声系数峰值主要与较小孔隙率单层结构的峰值有关。直接面向声源一侧的多孔材料层对全频吸声系数起主要作用。第一层为较高孔隙率的结构的宽频吸声性能较好，这是由于第一层材料为控制层，当较低孔隙率材料层位于第一层时，不论后面的材料层如何布置，都难以改善整体结构的高频吸声性能。对于孔隙率由高到低的结构，由于孔隙率大，胞孔多，声波更容易进入材料，又因为大孔隙率材料内部通道复杂，能够产生更多的散射和碰撞，能量损耗增加[12]，且后面叠加的小孔隙率材料使声波难以透射，从而有更好的吸声系数。

图6 不同梯度孔隙率结构对吸声系数的影响Fig.6 Influence of different gradient porosity structure on sound absorption coefficient

3.2 孔隙率梯度差对吸声系数的影响

基于3.1中的四种梯度孔隙率结构方案，取较高孔隙率为0.96，较低孔隙率分别为0.76、0.56、0.36、0.16。梯度差对吸声系数的影响如图7所示。

从图7(a)中可以看出，对于方案一，随着梯度差的增加，4 000-6 000 Hz频段的吸声系数逐渐增大，其他频率段的吸声系数逐渐减小。当较低孔隙率下降到0.26以下时，宽频吸声系数减小，这与图5中单层结构的吸声性能曲线在第一峰值处的规律一致。从图7(b)中可以看出，对于方案二，随着梯度差的增加，第一峰值逐渐增大且峰值点逐渐向低频移动，第一峰值频率在1 900 Hz左右，第二峰值大幅度降低。从图7(c)中可以看出，对于方案三，随着梯度差的增加，第一峰值逐渐增大，第一峰值频率约为2 700 Hz，3 000 Hz以上的高频吸声系数呈下降趋势。从图7(d)中可看出，对于方案四，其整体吸声性能曲线趋势与方案二一致，但其不同梯度差曲线第一峰值所在的频率更为紧凑。

(a) 方案一

孔隙率梯度差大能够显著提高吸声性能曲线的第一峰值，但其在高频处的吸声系数有明显降低，其中，较低孔隙率层作为分层材料的第一层时，材料在高频处的吸声系数大幅度下降，反之，第一层为较高孔隙率层时，高频处吸声系数下降缓慢。由此可知，高频处的吸声系数主要受第一层材料的影响。

4 算例验证

为验证以上结论的通用性与可靠性，另取两种弹性多孔材料：三聚氰胺泡沫、聚酯泡沫。其声学参数如表4所示。

表4 三聚氰胺泡沫与聚酯泡沫参数Tab.4 Parameters of melamine foam and polyester foam

取三聚氰胺泡沫总厚度为0.018 m，对于双层结构，各层材料厚度均为0.009 m，对于三层结构，各层材料厚度为0.006 m。取较高孔隙率为0.99，较低孔隙率为0.39，组成3.1中所述的四种结构方案，结果曲线如图8所示。

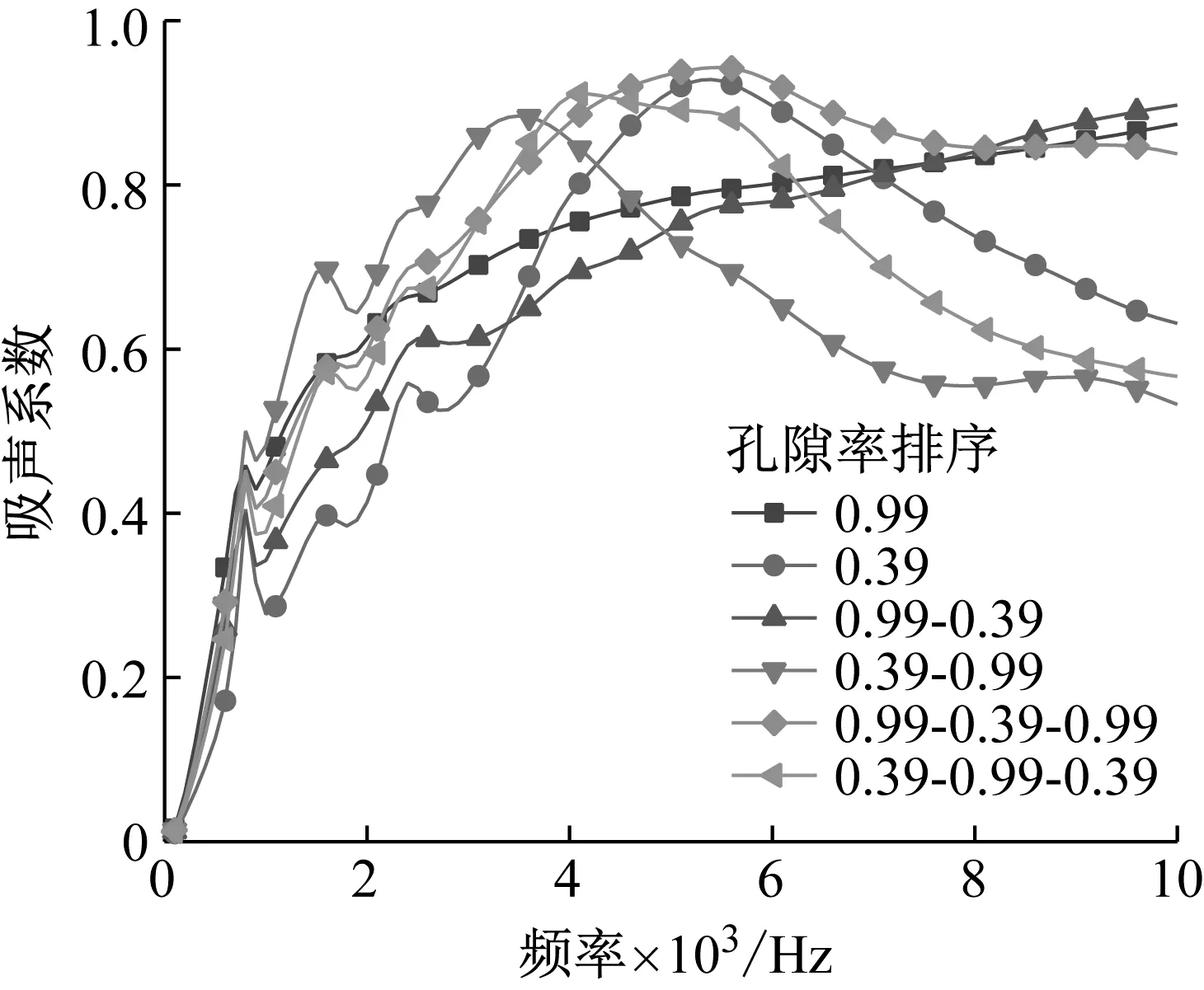
图8 不同梯度孔隙率结构对三聚氰胺泡沫吸声系数的影响Fig.8 Influence of different gradient porosity structures on sound absorption coefficient of melamine foam

从图8中可以看出，在100-10 000 Hz频段内，孔隙率为0.99的单层结构的吸声性能曲线未出现峰值，孔隙率为0.39的单层结构的吸声性能曲线峰值频率为5 400 Hz，所以方案一的曲线峰值延后，方案二、三、四的曲线峰值在5 400 Hz附近。对比图6与图8可知，不同梯度孔隙率结构对以上两种弹性多孔材料的影响规律一致。

取聚酯泡沫总厚度为0.024 m，对于双层结构，各层材料厚度均为0.012 m，对于三层结构，各层材料厚度为0.008 m。取较高孔隙率为0.98，较小孔隙率分别为0.78、0.58、0.38、0.18。梯度差对吸声系数的影响如图9所示。

(a) 方案一

从图9中可以看出，第一层材料的孔隙率较低时，高频吸声系数随孔隙率梯度差的增加而明显下降。对于方案一，随着梯度差的增加，4 000-7 000 Hz频段的吸声系数逐渐增大，其他频率段的吸声系数逐渐减小。对于方案二、三、四，随着梯度差的增加，第一峰值逐渐增大。在100-10 000 Hz频段内，通过对比图7和图9可知，聚氨酯泡沫和聚酯泡沫这两种弹性多孔材料的梯度差对吸声系数的影响一致。

通过对聚氨酯泡沫、三聚氰胺泡沫以及聚酯泡沫的梯度孔隙率结构的研究，证明梯度孔隙率结构对弹性多孔材料吸声系数的影响存在一定的规律，并且随着较低孔隙率单层结构峰值频率的增加，梯度结构对吸声系数的改善更为明显。

5 层厚优化设计

孔隙率梯度差对梯度弹性多孔材料吸声性能的影响比较直观，而厚度分布对吸声性能的影响规律则较为复杂。将弹性多孔材料吸声系数计算模型结合多岛遗传算法，对以上四种结构的厚度分布进行优化设计，获得宽频吸声系数最优时的参数数值。取较高孔隙率为0.96，较低孔隙率为0.36，总厚度为0.03 m，以100-10 000 Hz频段吸声系数的RMS值为目标函数，总厚度为约束条件。优化函数为

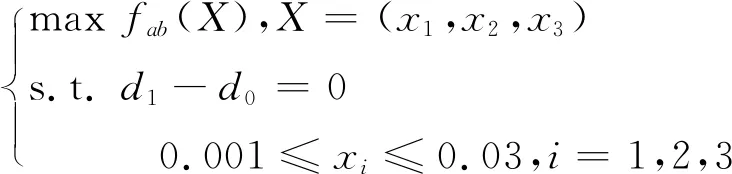
(22)

式中:fab为100-10 000 Hz频段吸声系数的RMS值；X为每层材料的厚度；d1为优化后的总厚度；d0为优化前的总厚度。

根据弹性多孔材料吸声系数理论计算模型以及多岛遗传算法，计算得到了四种梯度孔隙率结构的厚度参数优化值以及优化后的吸声系数-频率曲线，分别如表5及图10所示。

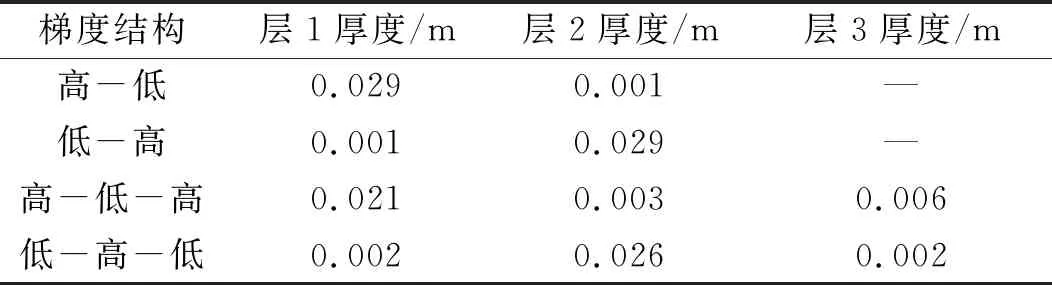
表5 厚度参数优化值Tab.5 Thickness parameter optimization value

图10 最优厚度分布的吸声性能曲线Fig.10 Sound absorption performance curve of optimal thickness distribution

对比图11中四种梯度孔隙率结构的厚度分布优化结果曲线，可以明显看出，当孔隙率由高到低再到高时，全频吸声性能最好。相对于孔隙率为0.96的单层材料，在没有明显吸声系数降低的情况下，3 000-7 000 Hz频率段内的吸声系数获得明显改善，而其它三种结构的吸声系数都在某一频率段内有一定程度的下降。

基于以上优化结果，选取方案三：孔隙率由高到低再到高的梯度结构，取3.2中所述的梯度差，吸声性能结果曲线如图11所示。

图11 最优厚度分布下的不同梯度差对吸声系数的影响Fig.11 Influence of different gradient differences under optimal thickness distribution on sound absorption coefficient

从图11中可以看出，随着孔隙率梯度差的增加，吸声系数峰值逐渐增加，谷值逐渐减小。在100-10 000 Hz频段内，孔隙率为0.96的单层结构的吸声系数RMS值为0.818。较小孔隙率从0.86逐级减小至0.16时，吸声系数的RMS值分别为：0.819、0.821、0.823、0.826、0.830、0.836、0.844、0.852。由此可知，对于上述结构，梯度差越大，全频吸声系数越高。

不同大小的孔排列在一起，形成喇叭状或沙漏状的结构，有利于声波能量的耗散。通过合理设计孔隙率梯度差和层厚，可充分利用不同孔隙率材料的峰值特点以及厚度对吸声系数的影响，使得材料有更好的全频吸声效果。因此，可以根据在不同频率段内对吸声性能的需要来确定最优的孔隙率梯度差及厚度分布，设计出符合吸声性能要求的梯度弹性多孔材料。