结构振型几何辨识及应用研究

董建华 宋 乐 骆拴青

(1.河南能源化工集团重型装备有限公司，河南 郑州 450045；2.河南省兴豫建设管理有限公司，河南 郑州 450001； 3.河南大象建设监理咨询有限公司，河南 郑州 450005)

结构振型几何辨识及应用研究

董建华1宋 乐2骆拴青3

(1.河南能源化工集团重型装备有限公司，河南 郑州 450045；
2.河南省兴豫建设管理有限公司，河南 郑州 450001； 3.河南大象建设监理咨询有限公司，河南 郑州 450005)

推导了基于振型的位移、应变和应力展开公式，介绍了振型的分类方式，并根据振型的几何判别标准，分析了高宽比对结构振型的影响规律，得出了一些有价值的结论，以供参考。

振型，高宽比，方向系数，特征参量

0 引言

结构的振型和频率仅与其本身的质量和刚度有关，与其他因素无关，故常称之为特征参量。振型描述了质量和刚度之间的相对比值关系，表征了结构质量和刚度在空间上的分布情况。又因为振型为位移展开的完备正交基，以位移为桥梁，可将内力和应力在振型坐标基上投影。因此，提高对结构变形有利的振型，降低对结构变形不利的振型。利用结构振型指导结构概念设计和构造设计，可分别从整体和局部的范畴来控制结构设计[1，2]，使结构满足安全、适用和耐久性的要求。利用振型指导结构设计，关键在于振型的量化和振型位移的展开问题。计算位移展开所需振型数可由范数确定[3-5]。Hiroki Yamaguchi[6]、布占宇[7]和王福智[8]等人对振型进行过研究，提出利用振型方向系数对各振型进行量化，取得了较好的研究成果。但振型方向系数仅能给出振型中某一种振动特性，通过分析发现，振型中某单一振型，常常是两种或两种以上振型单元的耦合，只不过是某一振型单元所占比例较大而已。如能对振型单元进行量化，给出不同振型单元所占比例，通过振型单元比例的大小定义振型，再利用振型指导结构概念设计，可从宏观上把握结构的整体力学性能，使结构设计趋于合理。

1 基于振型的位移、应变和应力展开公式推导

振型是结构位移的完备正交基，任何位移都能以振型为坐标基展开。将位移表示为振型和振型幅值乘积的形式，如式(1)所示：

D=a1φ1+a2φ2+…+anφn

(1)

其中，D为位移向量；φn为结构的振型；an为位移展开在各振型中的振幅。利用振型的正交性，an值为：

(2)

又知应变与位移之间的微分方程为：

{ε}=[L]{D}

(3)

其中，[ε]为应变矩阵；[L]为表示位移和应变之间关系的微分算子矩阵。应力与应变的关系式为：

{σ}=[K]{ε}

(4)

其中，{σ}为应力矩阵；[K]为刚度矩阵；{ε}为应变矩阵。

通过位移矩阵，应变矩阵和应力矩阵都可以依振型矩阵展开。某振型上应变和应力的展开式为：

{εn}=anφn[L]{D}

(5)

{σn}=[K]{ε}=anφn[K][L]{D}

(6)

从式(3)～式(6)可以看出，对于构件，只要位移已知，就可以求出相应的应变和应力在振型上的投影值，对应力在面内或体积内积分，可求出相应的内力值。位移在振型上投影的幅度值an反映了外界荷载对各振型的作用效应，因此对an分析就能显示荷载效应在振型间分配大小。

2 振型的分类

通常，根据振型的振动方式以及对结构受力的影响，有不同的分类方式，下面将振型按两种方式进行分类。

2.1 单一振型和复合振型

如果某一振型由一种变形方式构成，则为单一振型；如某一振型由两种及以上变形方式构成，则为复合振型，例如弯剪振型、弯扭振型等。

2.2 有利振型和不利振型

根据振型与位移之间的关系，对结构变形有利的振型称之为有利振型，例如平动振型和弯曲振型；相反，对结构变形不利的振型称之为不利振型，例如剪切振型、扭转振型，以及剪切或扭转振型与弯曲振型的复合振型，例如弯剪振型或弯扭振型等。不利振型极易引起剪切破坏或扭转破坏，破坏且呈脆性，使结构的安全可靠度降低，在结构设计时需加注意。

3 振型的几何判别标准

分析仅针对平面问题，讨论高宽比对结构振型影响的一般规律。将结构进行有限元网格划分，单元在各振型中的变形形状只有三种，如图1～图3所示，分别对应结构的拉伸或压缩变形、剪切变形和弯曲变形。图1表示单元仅在某一个或两个方向上拉伸或压缩，没有剪切变形的发生，通常对应于竖向振动。图2为单元的剪切变形，变形特点为单元两对边相互错动，大致保持平行。图3为弯曲振型单元，四边中有两边呈明显的受拉边和受压边，另两边也不再保持平行。振型的判定就变成对这三种变形单元的几何辨识。由初等几何学知：矩形振型单元的判定不仅要求两对边相互平行，而且要求角“1”保持为直角，满足这两个条件的为矩形振型单元；平行四边形振型单元仅要求对边保持平行即可；振型单元凡不属于这两类振型单元的都归到弯曲振型单元范畴。根据以上判定准则，就可对不同阶次振型进行几何量化，统计各振型中不同变形单元所占的比例，对平面振型振动方式有了量化标准。必须注意，对于图1和图2，线“1”与线“2”，线“3”与线“4”不可能完全满足平行定理，相应，线“1”与线“3”也不可能刚好满足正交条件，因此合理计算精度的设置直接影响单元振动方式的判别。判定精度设置的不同，振动方式各异，但对于某一固定高宽比结构，不同阶次间设置统一控制精度，识别不同振型中不同振动方式所占的比例，进而指导结构整体变形方式的设计，具有一定的指导意义。

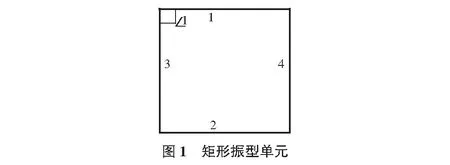
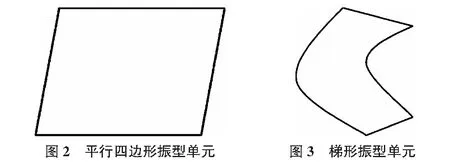
4 高宽比对结构振型影响分析

结构的高宽比不能太大也不能太小，太大造成结构稳定性较差，易引起倾覆；太小不能较好利用材料柔性性能，整体变形以剪切变形为主，钢筋混凝土或钢结构柔性变形性能得不到发挥。我国高层技术规程[9]规定，对于A级高度混凝土房屋，最大高宽比为6，对于B级高度混凝土房屋，最大高宽比为7，故高宽比分析范围为1～7。假定结构宽度为6 m，根据不同高宽比，计算相应的几何变形系数。定义判断线“1”和线“2”平行的系数为P1，定义判断线“3”和线“4”平行的系数为P2，定义判断角“1”为直角的系数为P3。P1和P2精度由振型一中最大值确定，P3以使竖向振动振型最大值确定，这样不同高宽比三个振型单元判断精度得到确定，如表1所示。根据各振型单元变形特征，编写了判定振型单元几何形状的有限元程序[10]“ModeIdentification”，高宽比1～7范围内前8阶振型三种几何变形单元所占比例如表2所示。

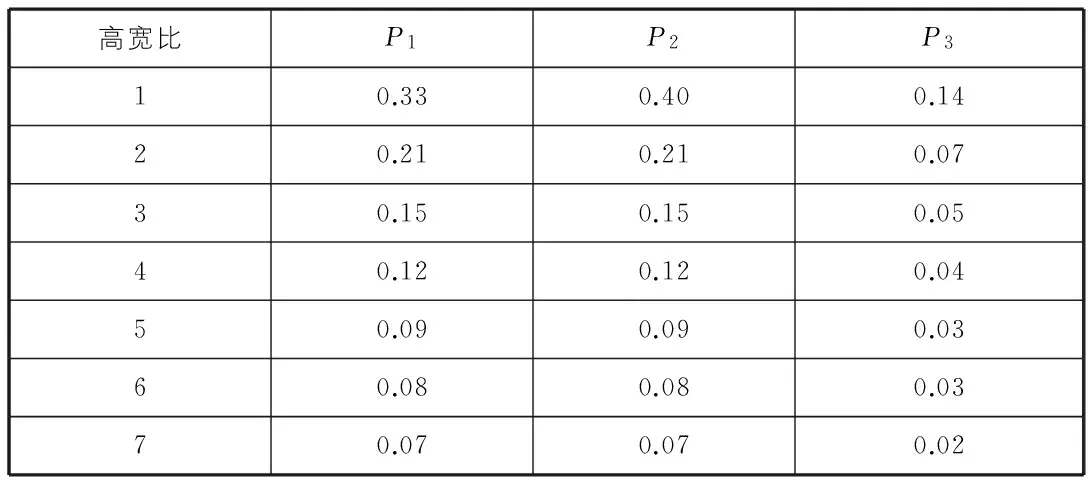
表1 不同高宽比振型判断精度

通过以上计算可以看出高宽比对振型影响规律如下：

1)综合考虑前8阶振型，随着高宽比的增大，结构振型逐渐由剪切型变形向弯曲型变形过渡，高宽比基本上以3为分界线，当高宽比小于3时，结构呈剪切型变形，不小于3时呈弯曲型变形。故对于砌体结构，材料性能呈现脆性，变形以剪切型为主，高宽比限制在3范围内[11]，此结论在振型分析中得到验证；而对于钢筋混凝土结构或钢结构，整体结构呈现柔性，有很强的耗能能力和变形能力，为了充分发挥材料性能，高宽比宜在3～7范围内，例如高层技术规程规定，对于筒体结构，高宽比不宜小于3。

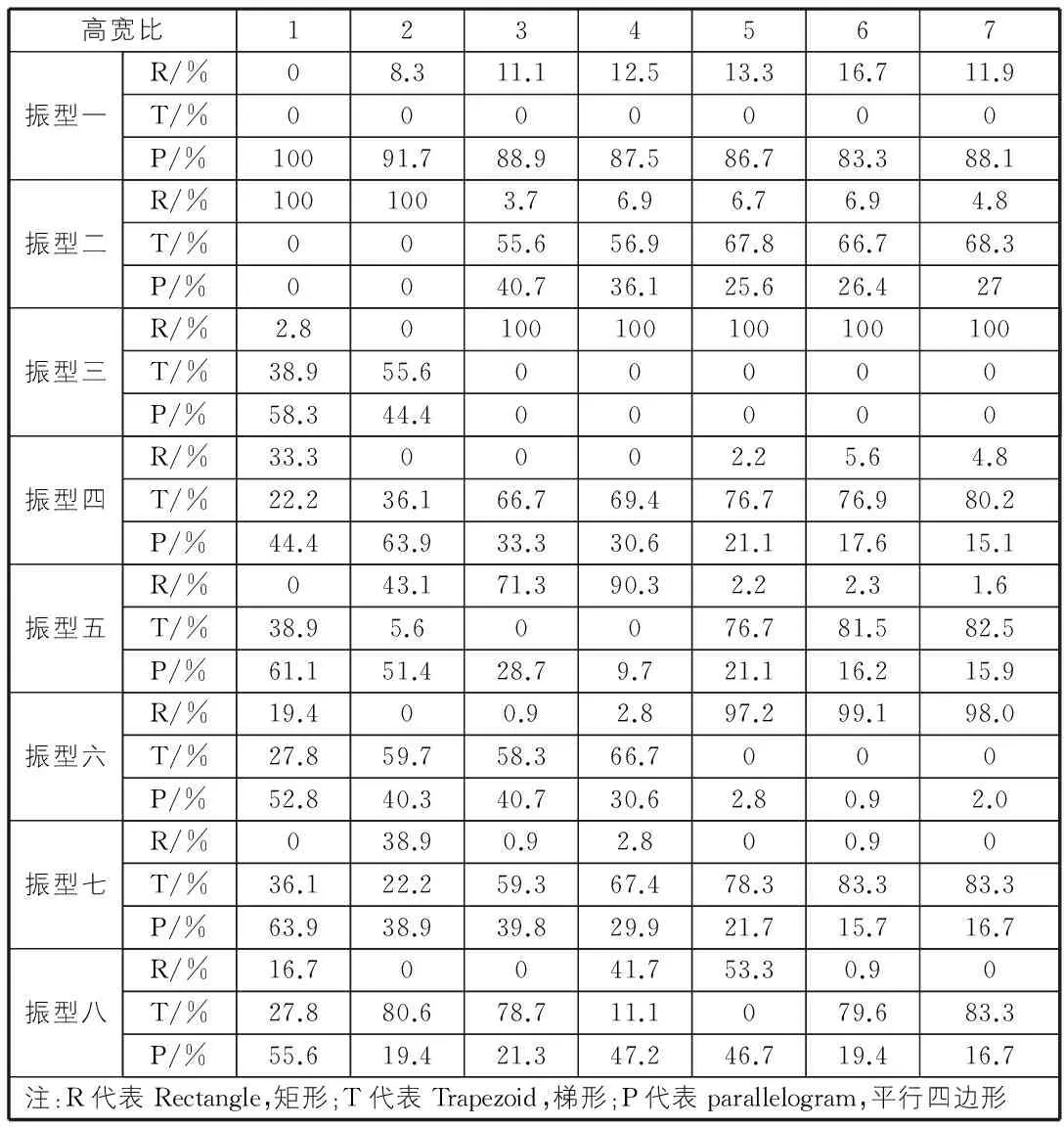
表2 不同高宽比前8阶振型变形比例

2)高宽比影响结构振型的振动形式和振型出现的先后顺序。当高宽比小于3时，第二振型为竖向振型，不小于3时第三振型为竖向振型。当高宽比等于1时，第四振型和第六振型为一阶和二阶双向弯曲振型；当高宽比等于2时，第七振型为一阶双向弯曲振型；当高宽比不小于3时前八阶振型再没有双向弯曲振型。当高宽比等于3和4时，竖向振动为第三阶和第五阶；当高宽比等于5，6和7时，竖向振动为第三阶和第六阶。

3)在高宽比容许范围内，前8阶振型基本上都是从剪切振型向弯曲振型过渡，高宽比越大变形性能越好，也越能发挥结构的耗能能力，因此利用振型可从宏观上把握结构的整体力学性能，利用振型指导结构概念设计。

4)当高宽比不小于5时，结构振型趋于稳定，表明结构振型有趋于“收敛”的特性，故利用振型指导结构设计从原理上来说是合理的。

5)利用振型的几何判别可以发现，结构的振型一般都不是完全某一振型组成，而是弯曲、拉压或剪切振型的组合，某一振型占优，这样可利用振型的几何辨识，更清楚认识结构的振型，指导结构设计。

5 结语

通过以上振型的几何辨识，可以得到以下结论：

1)对不同高宽比振型计算结果可以看出，除了竖向振动外，一般振型都不是某一种振型单独振动，而是和其他振型耦合振动，常以某一振型振动为主，其他振型振动为辅。

2)振型出现的阶次随高宽比变化而变化。随着高宽比的减小，不利振型提前。例如当高宽比不小于3时，竖向振动通常在第三阶出现，而小于3时，竖向振动提前到第二阶。

3)随着高宽比的增大，振型逐渐由剪切形振动向弯曲形振动方式过渡。结构振型变形也愈加变得合理。

4)振型振动方式判断精度在同一高宽比不同阶次振型下可为同一精度，不同高宽比振型精度不同，这为结构振型振动判断的基本依据。

5)通过以上几何方法，可对平面振型进行量化表示，对振型有了量化指标，为结构设计提供了更为科学的基本理论，指导结构设计。

6)本次分析仅针对平面问题，对于空间问题，还会出现扭转振型。对于空间问题，另文再进行讨论。

[1] 季三容，王东炜，赵 骞.基于模态分析的钢管脚手架平面支撑刚度研究[J].郑州大学学报(工学版)，2010，31(4)：31-35.

[2] 王东炜，张奇伟，王用中.基于模态分析的鄄城黄河公路大桥优化设计[J].郑州大学学报(工学版)，2010，31(6)：1-5.

[3] 庄 茁.连续体和结构的非线性有限元[M].北京:清华大学出版社,2008：538-540.

[4] 史荣昌，魏 丰.矩阵分析[M].北京:北京理工大学出版社,2010：177-199.

[5] 李清扬，王能超，易大义.数值分析[M].北京:清华大学出版社,1986：196-205.

[6] Hiroki Yamaguchi, Manabu Ito. Mode-dependence of structural damping in cable-stayed bridges[J].Wind Engineering and Industrial Aerodynamics,1997(72):289-300.

[7] 布占宇.斜拉桥地震响应分析中的索桥耦合振动和阻尼特性研究[D].杭州：浙江大学博士学位论文，2005.

[8] 王福智，王依群，邓孝祥.振型数的选取及扭转振型的确定[J].天津理工大学学报，2005,21(3):81-85.

[9] GBJ 3—2010，高层建筑混凝土结构技术规程[S].

[10] O.C.Zienkiewicz, R.L.Taylor. Finite element method for solid and structural mechanics[M].Elsevier(Singapore) Pte Ltd，2008.

[11] GB 50011—2010,建筑抗震设计规范[S].

Structure mode geometrical identification and application

Dong Jianhua1Song Le2Luo Shuanqing3

(1.HenanEnergyandChemicalIndustryGroupHeavyEquipmentCo.,Ltd,Zhengzhou450045,China;2.HenanXingyuConstructionManagementCo.,Ltd,Zhengzhou450001,China;3.HenanDaxiangSupervisionConsultingCo.,Ltd,Zhengzhou450005,China)

The paper induces the displacement of the model of vibration, strain and stress expansion formula, introduces the classification approaches of the vibration mode, analyzes the influential law for the height-width ratio on the structural vibration mode according to the geometric judgment standard of the mode, and achieves some valuable conclusion, so as to provide some reference.

mode of vibration, depth-width ratio, direction coefficient, characteristic parameter

2015-03-10

董建华(1978- )，男，工程师； 宋 乐(1988- )，女，助理工程师； 骆拴青(1976- )，男，高级工程师

1009-6825(2015)14-0035-03

TU311.1

A