基于随机Wiener过程的火炮身管剩余寿命预测

2021-05-07朱喜华李颖晖王群力

科学技术与工程 2021年5期

朱喜华, 李颖晖, 王群力, 汪君

(1.中国人民解放军95795部队，桂林 541002； 2.空军工程大学航空工程学院，西安 710038)

火炮是一种应用广泛的常规武器，身管是决定其性能的关键部件，也是寿命最短的部件之一，研究火炮身管的剩余寿命，不仅能够有效减少火炮的维修费用，降低发生风险的概率，也能为科学制订火炮维修计划提供参考和依据[1]，进而指导部队科学合理地使用火炮，提高部队平时和战时对火炮的科学管理水平。现代战争对身管类武器性能的要求越来越高，尤其是随着一些新型身管武器的研制和使用，火炮身管寿命问题日益凸显。身管寿命问题严重制约着火炮射击效果的发挥和维修保障水平的提高，已成为中外学者研究的热点[2]。身管失效是一个非常复杂的物理化学过程，无法直接预测身管的剩余寿命，一般通过与寿命密切相关的中间变量进行预测，其中膛线径向磨损量判别法一经提出，就获得了各国学者的普遍认可，至今仍是身管寿命实际评估预测最有效的方法。当前，身管寿命预测主要有两类方法，一是基于内弹道、熔化层或者挤进过程等理论推导的预测模型；二是基于退化数据进行数据外推的预测模型，如统计学预测法、蒙特卡罗预测法、神经网络预测法、支持向量机预测法等[3]。

选择恰当的寿命预测方法和模型有利于准确预测身管和火炮的寿命状态，进而科学制订维修保障计划。神经网络、支持向量机等预测方法没有考虑身管失效过程中的各种不确定因素，只是对性能退化数据的变化趋势进行预测，预测结果为某一确定值，不能综合反映各种随机因素的影响。随机Wiener过程是应用广泛的性能退化模型，能较好地描述非单调性能退化过程，反映性能退化过程中不确定因素的影响，且具有较强的计算分析能力[4-6]。因此，现将随机Wiener过程应用于某型火炮身管的剩余寿命预测，并以身管内径烧蚀磨损量作为预测的性能参数，探索一种火炮身管剩余寿命预测的新方法。首先，介绍随机Wiener过程的基本原理；其次，详细分析预测模型参数的极大似然估计和Bayesian更新方法；最后，在某型火炮身管的剩余寿命预测中进行应用和验证。

1 随机Wiener过程的基本原理

设连续时间随机过程X(t)为Wiener过程，则有

X(t)=λt+δW(t)

(1)

式(1)中：λ为漂移参数；δ为扩散参数，δ>0；W(t)为标准的布朗运动，即有W(t)～N(0,t)。

Wiener过程具有如下性质。

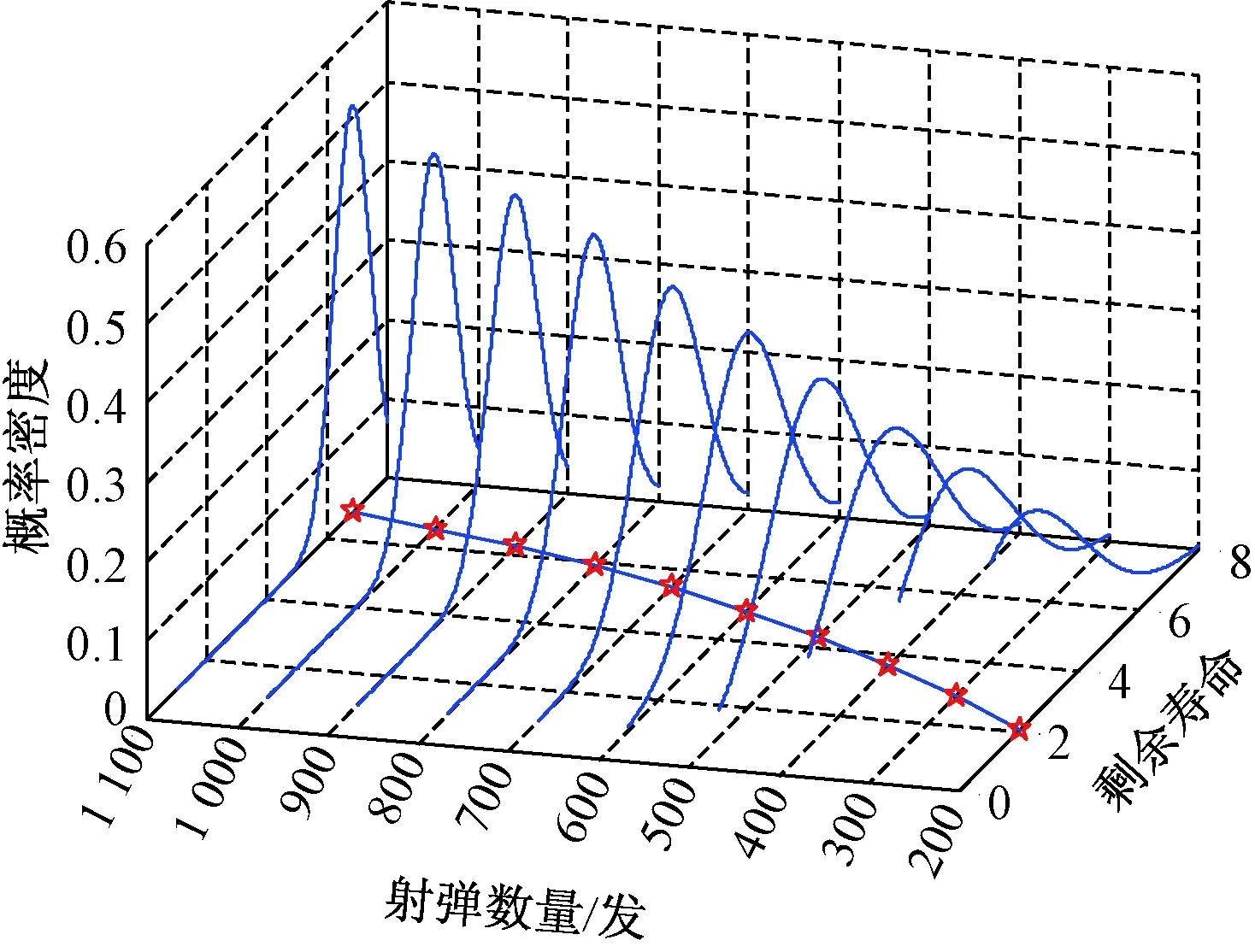
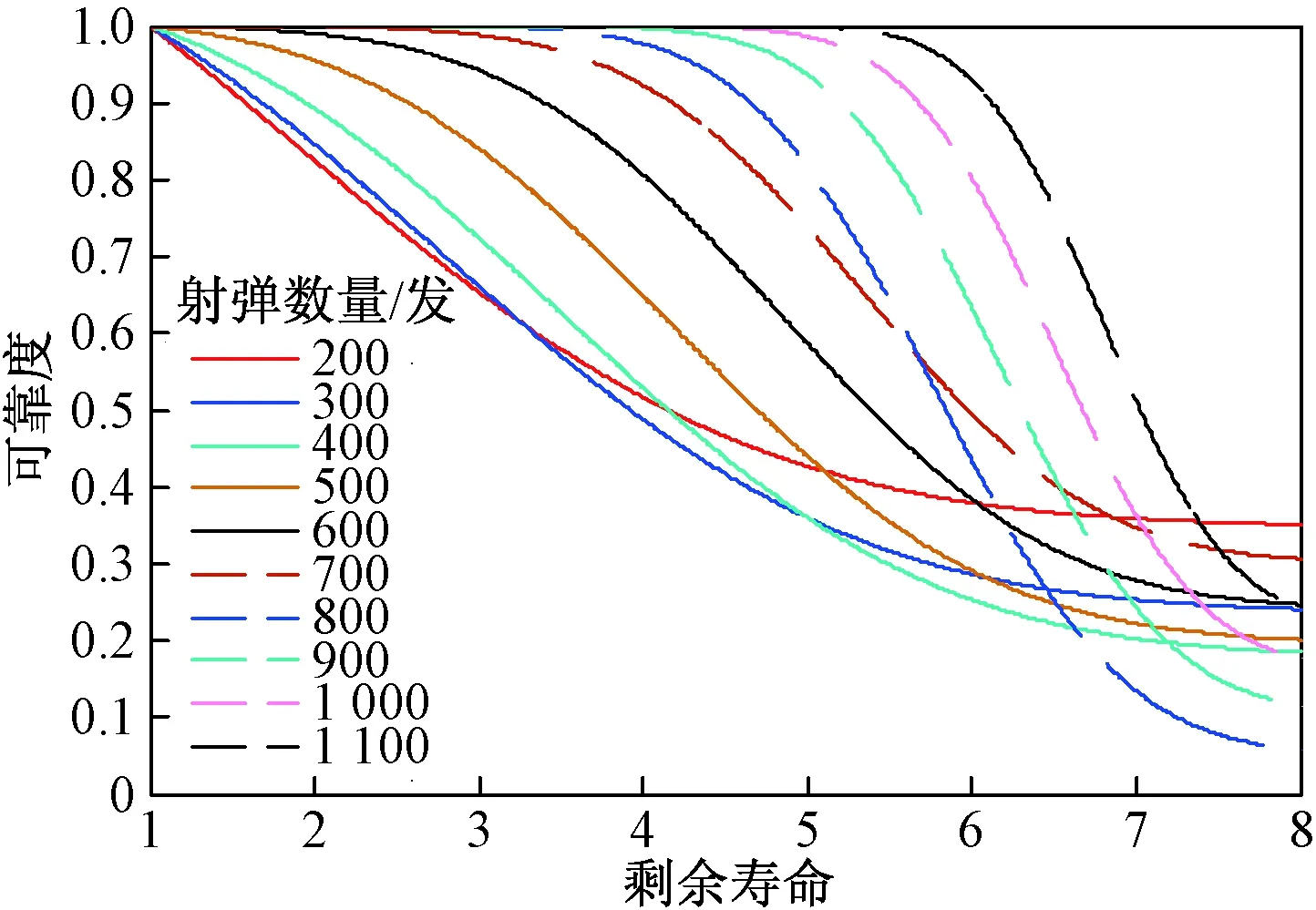
(1)X(t)为独立增量函数，并且对所有0≤s

(2)映射t→X(t)在正实轴上几乎处处连续。

(3)X(t)的初值为零，即X(0)=0。

其中，独立增量函数的定义为：(t1-s1)、(t2-s2)为随机抽取的两段不重叠的时间段，满足0≤s1

假设产品的失效阈值为常量ρ，寿命ζ定义为其性能参数X(t)首次达到失效阈值的时间，则有

ζ=inf{t|X(t)≥ρ}

(2)

经证明，Wiener过程的首达时间ζ服从逆高斯分布，其概率密度函数[7]为

(3)

Φ(λ,δ)dλdδ

(4)

(5)

产品的可靠度函数[10]为

(6)

式(6)中：Φ(·)为正态分布的分布函数。

2 模型参数的极大似然估计

假设产品在(t0,t1,t2,…,tm)时刻的性能参数序列为(y0,y1,y2,…,ym)，m为性能参数总量，设t0=0，y0=0，记Δyi=yi-yi-1为产品在时间段(ti-ti-1)内的性能退化增量，利用随机Wiener过程对性能退化过程进行建模，由Wiener过程的性质ΔWi～N(0,Δti)可得

Δyi～N(λΔti,δ2Δti)

(7)

式(7)中：Δti=ti-ti-1，i=1,2,…,m。

Wiener过程具有平稳独立增量的性质，则Δy1,Δy2,…,Δym的联合概率密度函数(似然函数)为

L(λ,δ)=f(Δy1,Δy2,…,Δym)=

f(Δy1)f(Δy2)…f(Δym)=

(8)

根据式(7)和式(8)，将似然函数L(λ,δ)对λ和δ分别求偏导，可得似然方程为

(9)

求解似然方程(9)可得

(10)

3 模型参数的Bayesian更新

由于处在高温高压的恶劣工作环境中，火炮身管的性能退化过程存在着诸多不确定性。通过采用Bayesian方法，利用性能退化数据实时更新参数的概率分布，可以降低不确定性对剩余寿命预测结果的影响。

设在第k个性能退化阶段，单个火炮身管的实时性能退化数据为

Δyk=[Δy1,k,Δy1,k,…,Δymk,k]

(11)

根据Bayesian公式可计算得到在第k个性能退化阶段，参数λ和ω(ω=δ2)的后验分布为

π(λk,ωk|Δyk)∝l(Δyk|λk,ωk)π(λk,ωk)

(12)

式(12)中：π(λk,ωk)为第k个退化阶段中退化模型参数的先验分布；(λk,ωk)为实时退化数据的概率密度函数；π(λk,ωk|Δyk)为退化模型参数的后验分布。

根据共轭先验分布的性质，可得出在第k个性能退化阶段，模型参数λ和ω的后验分布[11]为

(13)

其中，

(14)

(15)

(16)

(17)

同理，根据性能退化数据，可以实时更新所有已知退化阶段中的退化模型参数分布。

4 火炮身管的剩余寿命预测

烧蚀磨损直接关系到火炮身管的使用寿命，也是火炮在设计和使用维护过程中不可忽视的重要因素。火炮身管内弹道性能的改变量与烧蚀磨损的具体过程无关，只与烧蚀磨损的程度有关[2]。以火炮膛线某条阳线起始部位为检测固定点，当该位置的身管内径烧蚀磨损量Δd达到或超过允许最大值Δdmax时，身管寿命终止。以某型火炮为研究对象，其身管固定点内径烧蚀磨损量随射弹发数的增加而增加，如表1所示[3]。参照文献[12]，该型火炮的内径磨损量最大允许值取为6 mm，即有失效阈值ρ=6。

火炮内径烧蚀磨损量随着射弹数量的增加而增加，如图1所示。由图1可知，火炮身管内膛的烧蚀磨损随着射击次数的增加而愈加严重。

表1 某型火炮身管固定点内径烧蚀磨损量与射弹数量的关系Table 1 The relationship between the erosion and wear value of internal diameter of a gun barrel fixed point and the number of shots fired

图1 某型火炮内径烧蚀磨损量与射弹数量的关系Fig.1 The relationship between the erosion and wear value of internal diameter of a gun and the number of shots fired

为得到同类型火炮的内径烧蚀磨损量数据，以表1中的数据为蓝本(记为X0,k，k=1,2,…,14)，分别在其磨损量上叠加一随机数(初始状态均为零)，以模拟同类型其他火炮的烧蚀磨损情况，通过叠加随机数的方法生成四组数据(记为Xi,k,i=1,2,3,4)。根据火炮性能退化数据和文中剩余寿命预测的原理方法，可以得到该型火炮的剩余寿命概率密度函数如图2所示。

图2 某型火炮剩余寿命概率密度函数及点估计Fig.2 The residual life’s probability density function and point estimation of a gun

图3 某型火炮剩余寿命可靠度函数Fig.3 The residual life’s reliability function of a gun

由图2可以看出，在预测早期，由于性能退化数据较少，难以获得准确的参数估计结果，从而导致剩余寿命概率密度函数较“宽而矮”；随着射弹发数的增加，积累的性能退化数据逐渐增多，剩余寿命概率密度函数曲线越来越“窄而高”，表明剩余寿命预测的不确定性逐渐减小，准确度逐步提高。对应的可靠度函数如图3所示，图3中的10条可靠度曲线分别表示射弹数量为200～1 100发时的可靠度函数曲线。