一个一元高次不等式的推广及应用

四川师范大学数学科学学院 (610068) 纪定春 夏逸天 周思波

伯努利不等式，在高考数学和竞赛数学中具有广泛的应用，但直接运用伯努利不等式显得有些不太方便，需要将伯努利不等式(1+x)n≥1+nx(其中x>-1，n∈N*，当且仅当x=0时，取等．)变成xn≥nx-(n-1)(其中x>0，n∈N*，当且仅当x=1时取等．)的形式．为了使不等式“xn≥nx-(n-1)”的应用范围更广，考虑通过引入参数的方式将其推广．接下来，将给出该不等式的推广和应用．

1.不等式的推广

2.不等式的推广应用

例1 (2019年高考数学理Ⅰ卷23题)设a，b，c为正数，且满abc=1．证明：(Ⅰ)略；(Ⅱ)(a+b)3+(b+c)3+(c+a)3≥24．

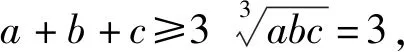
例2 (2017年高考理科Ⅱ卷23题)已知a>0，b>0，a3+b3=2，证明：(Ⅰ)略；(Ⅱ)a+b≤2．

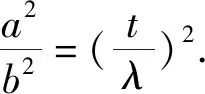
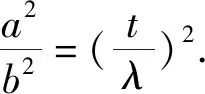
例5 已知正实数x，y，z满足x2+2y2+3z2+4w2=100，求xy+xz+xw+yz+yw+zw+x+32y+83z+154w的最大值．

3.结语

通过上述对伯努利不等式的推广和应用，可以发现，引入参数能够起到简化运算的效果，可以将高次的幂不等式问题转化成次数较低的幂不等式问题来解决，这极大的降低了高次不等式的证明难度．其中，对参数形式的伯努利不等式tn≥n·λn-1t-(n-1)λn，可以根据其取等号的条件“λ=t”，确定参数λ的值，进而达到恰当放缩不等式的目的．