数形结合：给思维展翅的机会

钱红娟

摘  要：数形结合是数学中的重要思想和解题方式，同时也是转换思维的主要手段，能有效提升学生的解题能力。但是，当前的数学教学过多强调成绩，而忽视了对学生数学思维能力的培养。教师要转变教学思想，以提高教学效率。

关键词：初中数学;数形结合;一次函数

一次函数是初中数学的重要内容，也是渗透数形结合思想的生动范例。教师可以从两个方面来组织教学，一方面，以数解形，将“形”的本质展露出来;另一方面，以形助数，把抽象的“数”变成可以亲近的“形”。在教學过程中，教师要做到授人以渔，即让学生感知数形结合思想，并巧妙地利用其解决问题。

一、以数解形，拨动学生的创新思维

创新思维是学生重要的思维能力，数形结合能为创新提供媒介，敦促其生成。

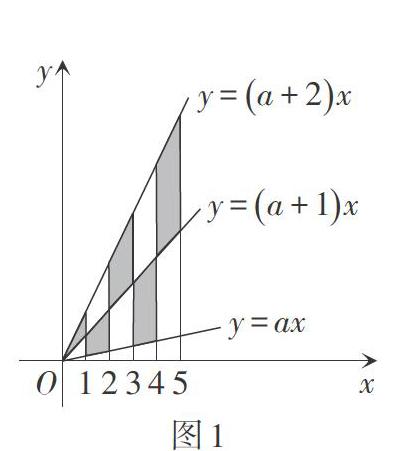
题目1  如图1，x轴上有五个点，它们的横坐标依次为1，2，3，4，5，分别过这些点作x轴的垂线与三条直线[y=ax，y=a+1x，y=a+2x]相交，其中[a>0]。则图1中阴影部分的面积是多少？

大部分学生看到题目后会知道这是一道函数题，于是从已知的横坐标入手进行解题，分别将x = 1，2，3，4，5带入三个直线解析式，并求出相应的纵坐标，进而利用相关数据求得结论。虽然这种做法可以得到正确答案，但是却非常烦琐。为此，教师可以在前面的教学基础上建议学生从几何图形的角度去思考这个问题，将零散的图形通过之前学过的平移聚集在一起。图1中的阴影面积与相对应的空白面积并不能直观看出同样大，要想平移，需要先证明两者面积一样大。通过计算，可以发现相邻两条平行于y轴的直线内的阴影与空白图形的对应边（三角形底边，梯形的上底和下底）相等，且高都为1，根据对应的面积公式，可求得对应图形的面积相等，进而确定平移后的阴影面积就是直线[y=ax，y=a+1x]与直线[x=5]所围成的三角形的面积，由此可以快速计算出图中阴影部分的面积。函数是代数中比较复杂的问题，引导学生利用数形结合解决相关问题，不仅可以简便计算、提高解题的正确率，而且还可以拓宽学生的解题思维，提升学生的数学学科核心素养。可见，解题的关键在于创新思维，而数形结合为创新思维提供了土壤。

二、以形助数，激励学生的扩散思维

数形结合能成为学生思考的一个聚点，学生能由数想到形，也可以由形想到数，这就是扩散思维的形成过程。

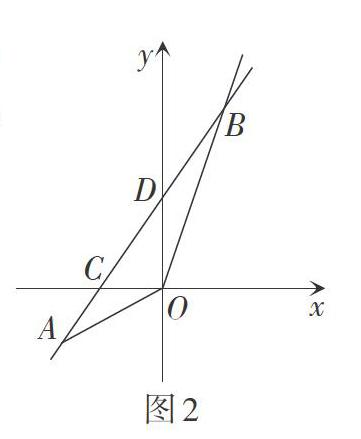
题目2  如图2，已知一次函数[y=kx+b]的图象经过[A-2，-1，][B1，3]两点，并且交x轴于点C，交y轴于点D。

（1）求一次函数解析式;

（2）求线段CD的长;

（3）求∠AOB的度数。

第（1）小题根据两点确定一条直线，用待定系数法即可解决问题，考查了学生对知识的识记能力。第（2）小题要求线段CD的长，可以根据点C，D的坐标所表示的几何意义得到线段OC，OD的长度，再由勾股定理求CD的长度，考查了学生综合运用知识的能力。第（3）小题，由于△AOB是钝角三角形，直接求∠AOB的度数比较复杂，怎样分散难点呢？我们可以先求出∠AOB补角的大小，因为题中各点的坐标已知，故可以根据坐标的几何意义求线段的长度，再将思维进一步扩散，即利用勾股定理的逆定理将边的条件转化为角的条件。通过解题的过程不难发现，将问题情境扩散到平面直角坐标系这个大环境中后，可以由数的途径求得边长，再利用勾股定理这座桥梁，便可以简单地求出角的度数。

在一次函数中，对数与形进行思维扩散的终点就是图象，即看到数要联想与之相关的形，看到形则要尝试将其转变为简单的数。扩散思维就是要将数与形作为思考问题的左右手，缺一不可。

三、数形结合，培养学生的分析思维

数学学习的过程是学生分析能力发展的过程，也是学生由浅入深的学习过程，是学生不断借助外物思考的过程。

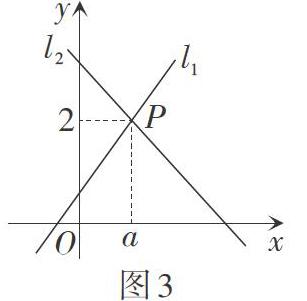
题目3  如图3，直线[l1：y=x+1]与直线[l2：y=mx+n]相交于点[Pa，2，] 则关于x的不等式[x+1≥mx+n]的解集为        。

解题时，学生先会根据两直线交点坐标求出[a=1，] 但是接下来只能根据已知坐标知道[m，n]之间的关系，并不能确定具体的解析式，代数的解题方法无法继续解法这道题目。这时教师需要启发学生将目光转向函数图象，让他们将[l1]的纵坐标大于等于[l2]的纵坐标的部分标出来，这样可以直观地看到包括点P在内的右边部分都是符合要求的。又因为点P的横坐标[a=1，] 所以这个不等式相对应的解集[x≥1]。可见，此题运用一次函数的图象和性质把数与形巧妙地结合起来。借图分析，又由图转数，不仅减少了计算量，而且提高了解题的效率。

四、结束语

数形结合就是让学生进行问题的转化，这就需要教师赐予学生一双“慧眼”，引导学生做到“眼中有形，心中有数”，从而以数解形、以形助数。

参考文献：

[1]白辉. 数形结合思想在初中数学教学中的渗透[J]. 科学咨询（教育科研），2020（4）.

[2]张玉翠. 数形结合巧运用  思维能力妙培养[J]. 名师在线，2020（10）.