LTE 和Wi-Fi 网络的双时间尺度未授权频谱划分算法

吴伟华，刘润滋，杨清海

（1.西安电子科技大学通信工程学院，陕西 西安 710071；2.西安建筑科技大学信息与控制工程学院，陕西 西安 710055）

1 引言

与授权频谱不同，未授权频谱对满足相关规定的任何运营商都是完全开放的。因此在未授权频谱上部署长期演进（LTE,long term evolution）技术网络以获得吞吐量的提升越来越流行[1]。但是，未授权频谱上的Wi-Fi 设备通过载波监听多路访问（CSMA,carrier sense multiple access）协议来实现对未授权频谱的占用，未授权频谱部署LTE 可能挤占Wi-Fi 的资源并造成Wi-Fi 吞吐量的下降。

一种常见的Wi-Fi 和LTE 的共存方法是将它们分别运行在2 个分离且不重叠的频谱上[2]。然而，对未授权频谱进行固定划分通常会带来很大的问题。由于LTE 和Wi-Fi 构成的异构网络是一个时变的动态网络，固定的划分方法很难自适应网络状态的动态变化[3]。因此，自适应的频谱划分策略成为实现LTE 和Wi-Fi 共存的必备选项。传统的自适应的频谱划分策略普遍采用基于快照形式的资源管理。传统算法如图1(a)所示，当网络状态发生变化时，需要重新对算法的输入进行初始化，并对算法进行迭代直至收敛到当前时隙的最优点。这种自适应策略的性能提升以终端设备和中央管理器之间较高的信令开销为代价[3-4]，例如，软件定义网络（SDN,software defined network）或网络功能虚拟化（NFV,network functions virtualization）。因此，需要设计一种低成本的自适应频谱划分策略。补偿算法如图1(b)所示，当网络状态发生变化时，自适应频谱划分算法仅需一次迭代就能找当前时隙的最优点。图1 中，纵坐标所示频谱划分为归一化频谱划分。

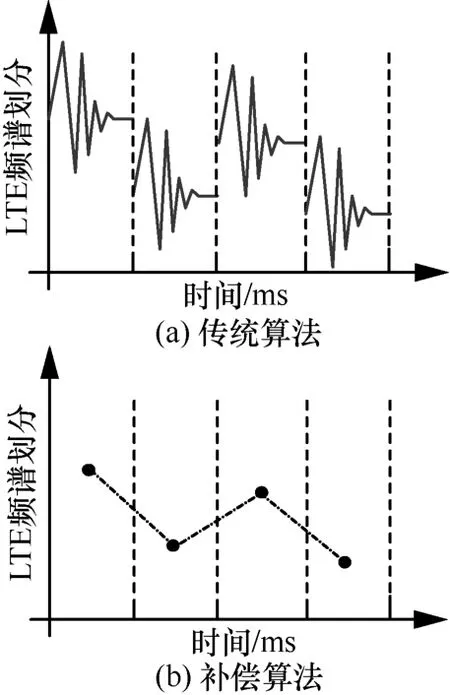
图1 频谱划分算法的不同迭代策略

此外，LTE/Wi-Fi 网络的不同信道状态信息（CSI,channel state information）只能在不同的时间尺度上获取。具体来说，所有Wi-Fi 设备以竞争的方式来占用相同频谱，这使Wi-Fi 的频谱划分决策取决于Wi-Fi 网络中的所有CSI。基于CSMA 网络的传输时延和不可靠性，难以实时获取全局CSI。与Wi-Fi 设备不同，LTE 设备工作在不同的专用频段上，因此其频谱划分决策仅取决于局部CSI。通过利用LTE 的上行传输链路，局部CSI 能够轻松地实时获取。如果对Wi-Fi 和LTE 频谱划分决策都进行纯小时间尺度的控制，则该算法必须实时地获取局部CSI 和全局CSI，这在实际的无线网络中很难实现。另一方面，如果对频谱划分决策都进行纯大时间尺度的控制，那么得到的算法必将过于保守，导致浪费很多瞬时的传输机会。根据上述观察，有必要对Wi-Fi 和LTE 的频谱划分决策进行混合时间尺度的控制。

本文提出了一种低成本的双时间尺度频谱划分算法，其中，Wi-Fi 频谱根据全局统计CSI 在较大的时间尺度上进行划分，而LTE 频谱根据快速变化的本地CSI 在较小时间尺度上进行划分。为了减少算法迭代和信令交换产生的开销，当网络状态在相应的大时间尺度和小时间尺度上发生变化时，仅对Wi-Fi 和LTE 频谱划分决策进行一次迭代。本文为双时间尺度的迭代算法设计了一个自适应补偿机制，以补偿算法输出与目标最优频谱划分决策之间的跟踪误差。最后，本文证明了算法的收敛性等同于一个虚拟随机动态系统的稳定，并通过计算虚拟随机动态系统稳定性，得出了双时间尺度算法收敛的充分条件。

2 系统模型

在LTE/Wi-Fi 系统中，后端的云服务器负责协调管理LTE 和Wi-Fi 在未授权频谱上的共存[3]。系统模型如图2 所示。

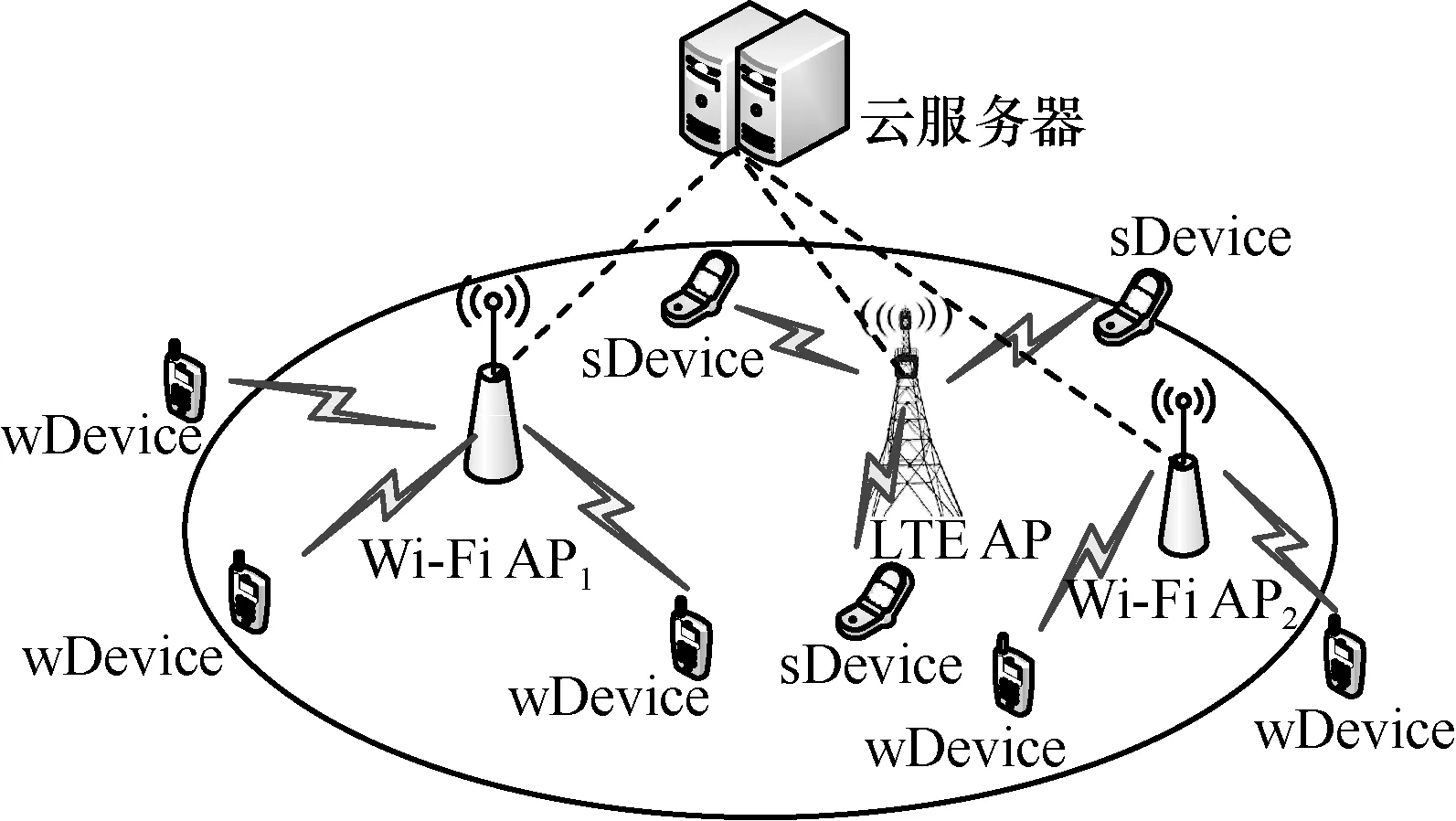
图2 系统模型

假设系统由一个LTE网络和M个Wi-Fi网络组成，其中，wDevice 表示连接到Wi-Fi 的移动设备，sDevice 表示连接到LTE 的设备，K m表示Wi-Fi 网络m服务的wDevice 集合，L表示sDevice 集合。在不失一般性的前提下，假设LTE 使用频分复用技术来承载所有的sDevice。集合Km中的wDevice 通过CSMA 协议来竞争未授权频谱并访问核心网络。Wi-Fi 网络吞吐量的计算方法由ICN（ideal CSMA network）模型给出[5]。根据ICN，不同wDevice 之间相互竞争和交互的结果可以抽象为传输机会，通常表示为1/|Km|，其中|Km|是集合Km中的设备数。假设整个未授权频谱的宽度为B，αm和ρl分别表示Wi-Fi 网络m和sDevicel的未授权频谱划分决策，则与Wi-Fi 网络m相关联的wDevice 设备k可实现的吞吐量为[5]

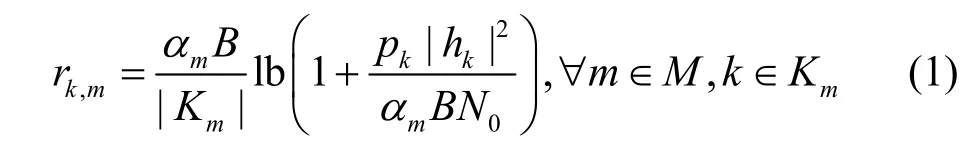
其中，pk为发射功率，N0为高斯背景噪声的功率谱密度，h为链路kk的信道增益。根据ICN 的计算方法，可得Wi-Fi 网络m的吞吐量为

由式(2)可以看出，Wi-Fi 网络m的吞吐量取决于和其相连的所有wDevice 的CSI。因此，Wi-Fi网络m的频谱划分决策αm取决于全局的CSI。

在LTE/Wi-Fi 网络中，LTE 能够为sDevice 设备l划分专用的频谱ρl。因此，sDevice 设备l的吞吐量为

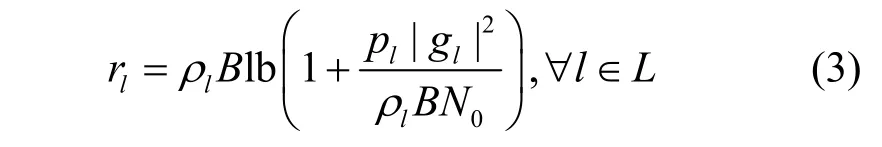
其中，pl为发射功率，gl为链路l的信道增益。从式(3)可以看出，sDevice 设备l的频谱划分决策仅取决于局部CSIgl。

为了描述简便，使用h来建模LTE 和Wi-Fi 网络中CSI 的动态模型，h=hlhs，其中，hl是大时间尺度信道衰落，hs是小时间尺度信道衰落。hs的动态变化由以下随机微分方程（SDE stochastic differential equation）建模[6-7]，如式(4)所示。

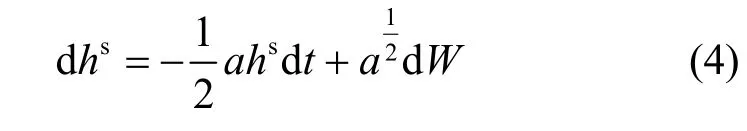
其中，a表示信道h的前后时间相关性，W表示一个具有单位方差的标准复合维纳过程。大时间尺度的CSI 模型可以建模为hl=Gh0D-ι，其中，ι表示路径损耗因子，G表示电路放大器和天线导致的功率增益常量，h0～CN(0,1)表示复高斯变量，D≥Dmin表示发射机和接收机之间的距离。因此，大时间尺度 CSI 的动态变化模型可以计算为dhl=-Gh0ιD-ι-1dD。假设发射机和接收机之间的相对移动速度为v，可得D=vt和dD=dv t。根据以上结论，大时间尺度的CSI 动态模型可以建模为

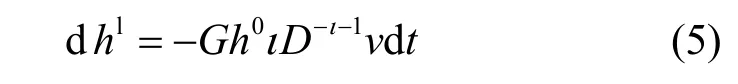
对于CSI 的动态模型，小时间尺度hs满足高斯平稳分布，因此|hs| 服从瑞利分布。对于大时间尺度CSI，表示hl的大时间尺度参数。

受限于Wi-Fi 网络的传输时延和不可靠性，它所需要的全局信息只能在相对较大的时间尺度上获得。因此，Wi-Fi 只能根据大时间尺度的CSI 信息{,}∀k∈K来进行频谱划分决策。LTE 网络能够实时获取本地CSI，则它可以根据2 个时间尺度的CSI 信息lsh=h h来进行频谱划分决策。在无线m网络中，评估每个网络的吞吐量仍然是确保所有共存网络可以维持一定服务水平的常用方法。因此，网络优化问题可以描述为LTE 和Wi-Fi 网络吞吐量的最大化问题，如式(6)所示。

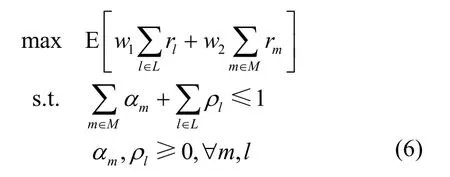
其中，w1和w2分别表示LTE 和Wi-Fi 的权重，即网络运营商对不同网络的服务偏好；约束条件表示划分的频谱不能超过总带宽。

3 双时间尺度迭代算法

3.1 基于补偿的频谱划分迭代算法

上述关于系统模型的讨论说明Wi-Fi 网络的频谱划分变量α=[α1,…,αM]T和LTE 网络的频谱划分变量ρ=[ρ1,…,ρL]T分别受到LTE 和Wi-Fi 网络中不同时间尺度CSI 的影响。根据分尺度的CSI 架构，可以将式(6)分解成不同时间尺度的子问题。

对于给定的Wi-Fi 频谱划分变量α，LTE 网络的频谱划分变量ρ可以通过求解式(7)得到。

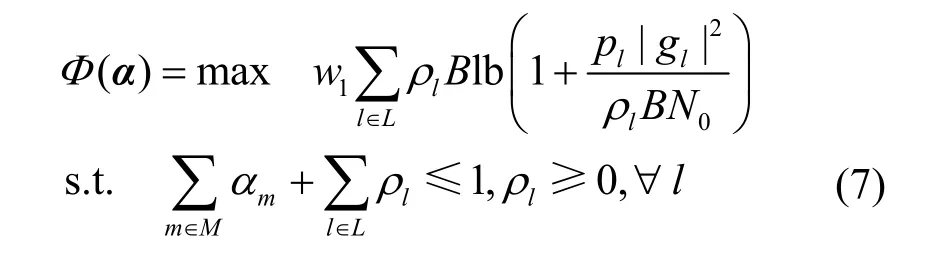
为了证明优化问题式(7)为一个凹问题，首先定义以下2 个函数

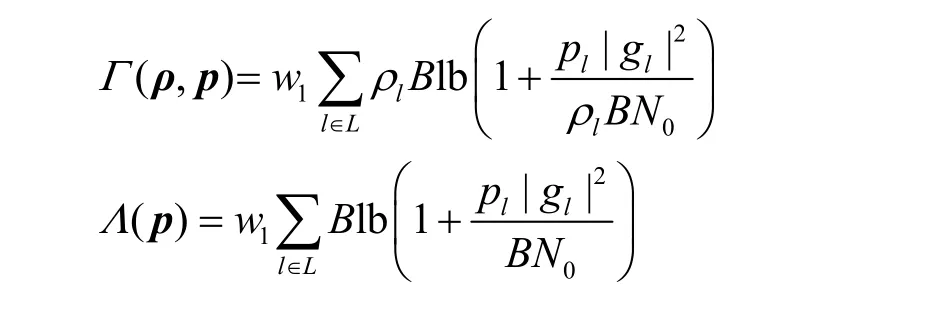
其中，p=[p1,…,pL]T。由于Λ(p)是对数函数的和，因此它是一个凹函数。不难发现Γ(ρ,p) 是Λ(p) 的透视函数，则Γ(ρ,p) 也是一个凹函数。式(7)优化问题的目标函数是给定p*的Γ(ρ,p*)，则目标函数也是一个凹函数。考虑到优化问题的约束条件为线性约束，则优化问题是一个凹问题。

对于给定的LTE 网络频谱划分变量ρ，Wi-Fi网络的频谱划分问题可以描述为

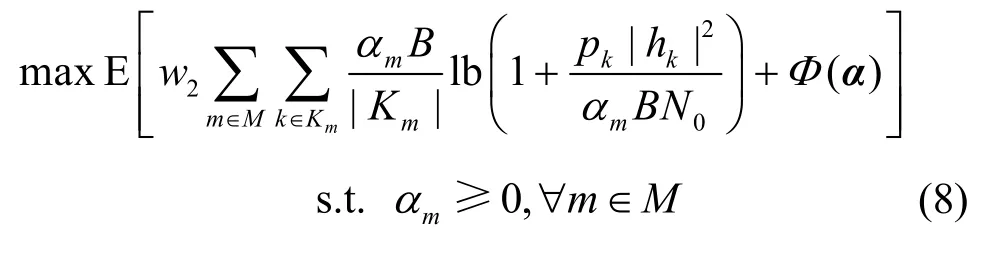
式(8)问题可以看作在给定LTE 网络频谱划分变量下的式(6)问题。用式(7)问题中同样的证明方法可以证明式(6)问题是一个凹问题，则式(8)问题也是一个凹问题。

下面，分别介绍如何解决这2 个凹问题。首先，给出LTE 网络频谱划分问题的拉格朗日形式为

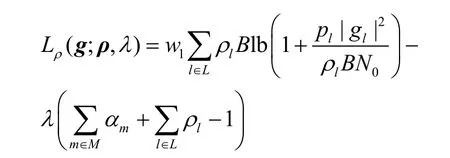
其中，g=[g1,…,gL]T，λ为拉格朗日乘子。求拉格朗日函数Lρ(g;ρ,λ)关于ρ和λ的导数，可以得到

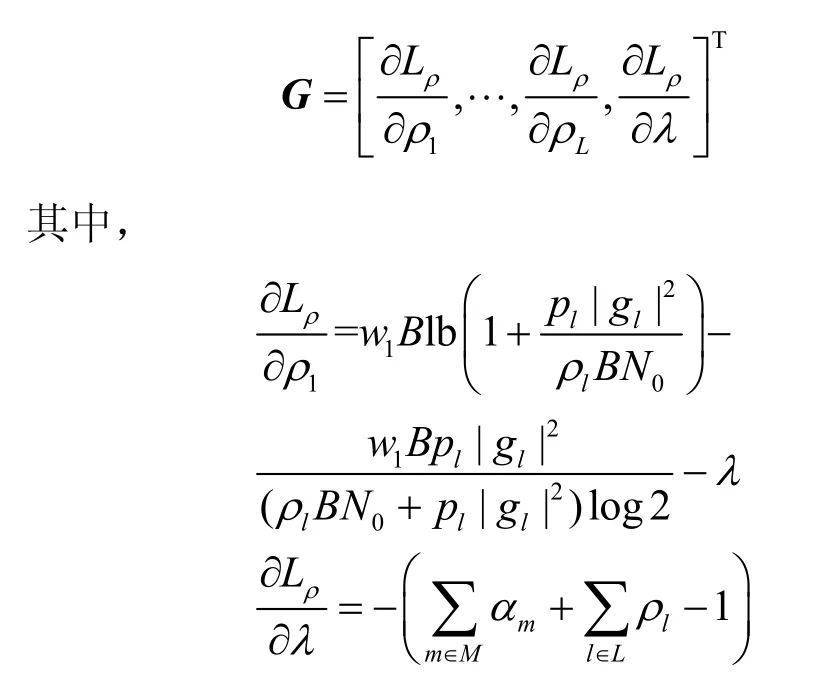
用原始对偶算法来搜索频谱划分的最优值，即得到迭代算法为

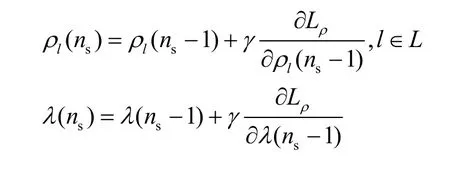
其中，γ为步长参数，ns为时隙索引。为了表示方便，令x=[ρT,λ]T表示LTE 频谱划分变量，则LTE频谱划分的迭代算法可以表示为

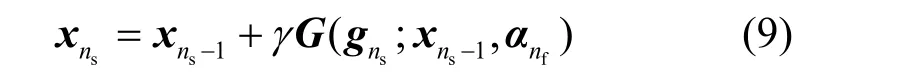
其中，nf为帧索引。

对于Wi-Fi 网络频谱划分问题，将式(8)问题的最大化表示为

则Wi-Fi 频谱划分的迭代算法可以设计为

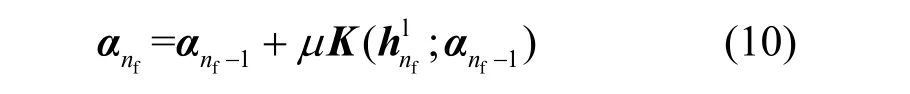
其中，μ为步长因子。

根据不同CSI 的获取时间尺度，将网络的运行时间划分为帧和时隙，每一个帧包含Ns个时隙。则LTE 的频谱划分算法和Wi-Fi 的频谱划分算法分别在每一个时隙和每一帧进行一次迭代。算法的迭代尺度如图3 所示。

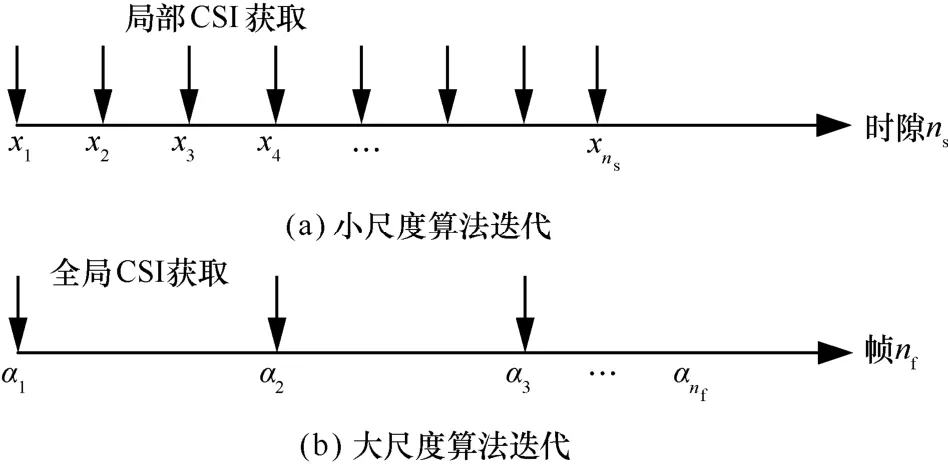
图3 算法的迭代尺度

算法的跟踪性能如图4 所示，其中纵坐标所示频谱划分为归一化频谱划分。客观上，随机优化式(6)问题一定存在一个和随机信道状态相关的最优解。当不同时间尺度的随机信道状态发生变化时，最优解（也称为均衡点）在随机信道状态的驱动下动态变化。由于本文设计LTE 的频谱划分算法和Wi-Fi的频谱划分算法分别在每一时隙和每一帧只进行一次迭代，并且信道状态也在随算法的迭代而变化，因此迭代算法的输出解很难跟踪均衡点的动态变化。将算法的输出解和均衡点之间的误差定义为跟踪误差。不难理解，跟踪误差的存在导致算法很难收敛，因此有必要研究算法的跟踪性能。

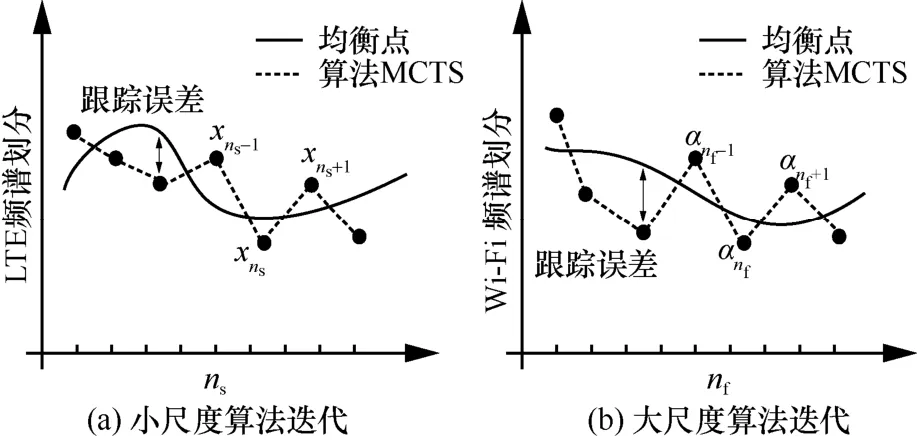
图4 算法的跟踪性能

为了分析方便，可以将不同时间尺度的离散迭代索引ns和nf映射到实数域，即sns=γns和snf=μnf。则算法迭代的轨迹可以用以下连续方程来描述

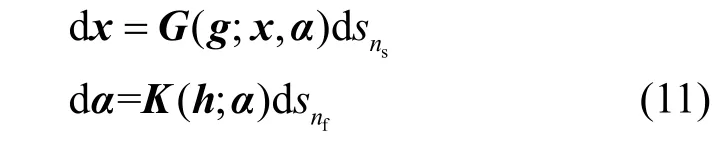
给定时隙的长度为τ，则帧和时隙的离散迭代索引分别为ns=t/τ和nf=t/τNs，因此，实数sns和snf与时间t的关系可以表示为

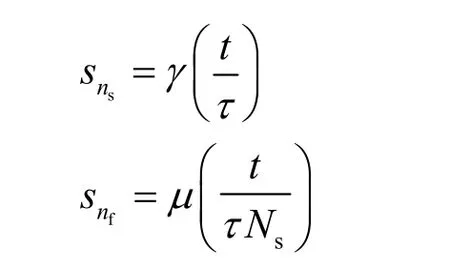
如果将时隙的长度看作一个单位，则式(11)可以表示为

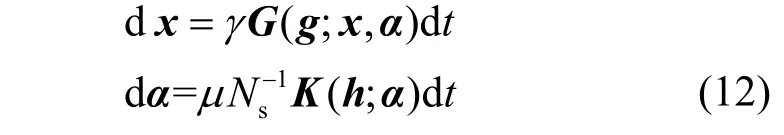
根据式(11)和式(12)的建模分析，离散的算法迭代可以抽象为平均连续时间动态系统（MCTS,mean continuous time dynamic system），如图4 中的虚线所示。算法的均衡点(x*,α*)一定满足G(g;x*,α*)=0和K(h;α*)=0。事实上，当网络中的CSI 为静态时，均衡点是固定不变的。然而在时变的无线网络中，均衡点随着随机CSI 的变化而变化。根据最优条件（G(·)=0和K(·) =0）和隐函数定理，均衡点的动态变化过程可以由以下MCTS 建模

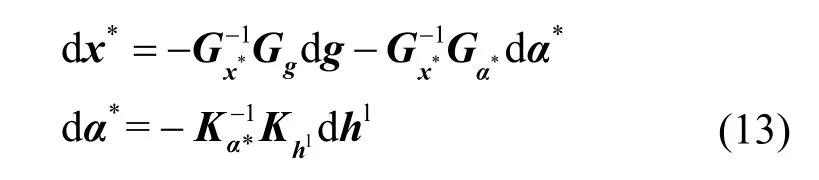
将式(12)中的算法迭代和式(13)中均衡点相减可以得到跟踪误差为

从式(14)和式(15)可以看出，当dg和dhl都为0时，跟踪误差可以收敛为0。然而，动态随机变化的CSI 会对算法的迭代产生持续的扰动，这会导致跟踪误差(xe,αe)很难收敛到0，因此迭代算法的输出很难跟踪均衡点的变化。为了提高算法的跟踪性能，可以为式(12)中的算法设计补偿项来抵消dg，dhl和dα*为对算法的迭代产生的扰动。基于这点考虑，设计基于补偿的频谱划分迭代算法，如式(16)和式(17)所示。

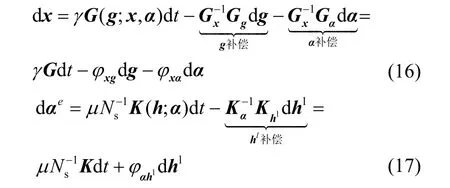
3.2 算法的收敛性分析

在设计式(16)和式(17)中的补偿机制时，补偿项φxgdg、φxαdα和φαhldhl并不是根据均衡点(x*,α*)得出的，而是用算法的当前输出值(x,α) 取代。这是因为在算法的运行过程中均衡点是不可能提前得到的，因此补偿项只能根据算法的当前输出值来计算。不难理解，根据算法当前输出值设计的补偿算法并不符合根据式(14)和式(15)得到的理论值。因此，仍然不能确定得到的补偿算法是否能实时地跟踪均衡点的变化。为了研究补偿算法的跟踪性能，首先计算补偿算法和均衡点之间的跟踪误差为

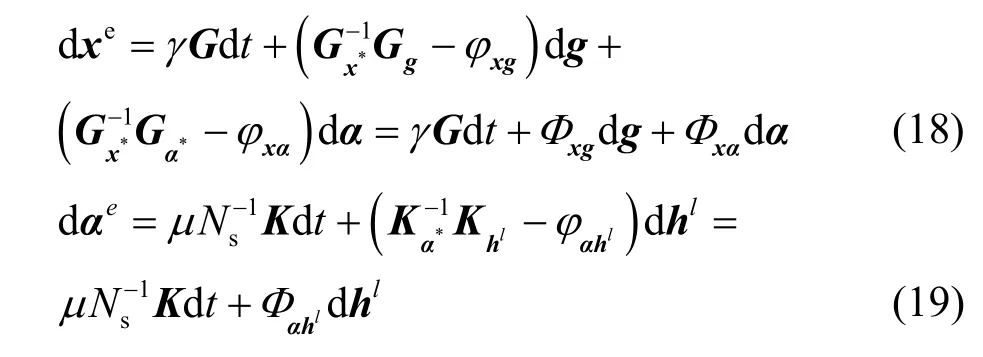
然后，式(4)和式(5)代入式(18)和式(19)，随机误差可以动态建模为式(20)所示的虚拟随机动态系统（VSDS,virtual stochastic dynamic system）。

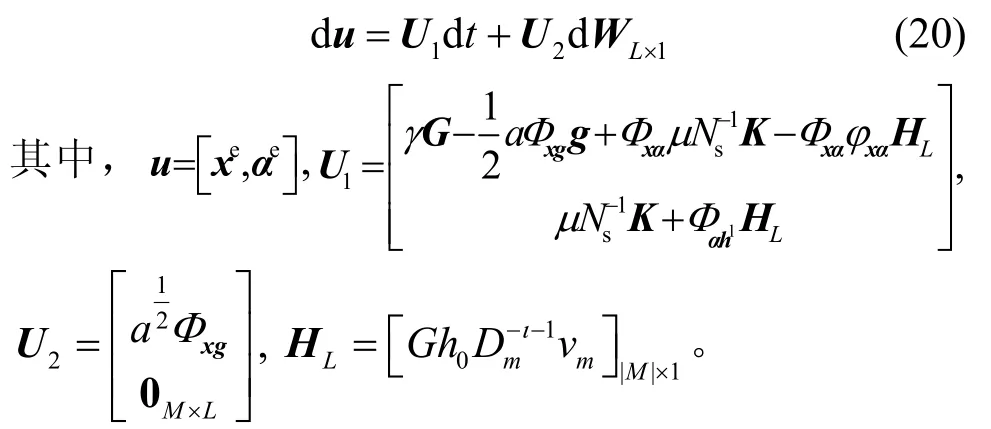
若式(20)中的VSDS 能够在(0,0) 处逐渐稳定，则跟踪误差(xe,αe) 能够收敛到(0,0) 。因此，式(20)表明基于补偿的频谱划分迭代算法的收敛等同于VSDS 的稳定。VSDS 的稳定性可以由李雅普诺夫稳定性理论来证明[8]。定义一个关于VSDS 状态u的李雅普诺夫能量函数为

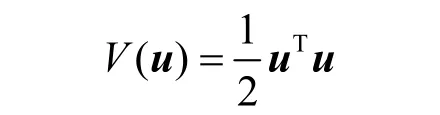
则V(u) 的李雅普诺夫漂移可以由引理1 给出。

引理1假设随机过程u可以由以下SDE 建模[7]

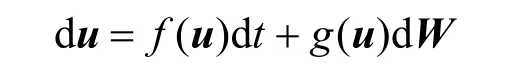
其中，W是一个标准的复合维纳过程，则V(u) 的李雅普诺夫漂移可以计算为

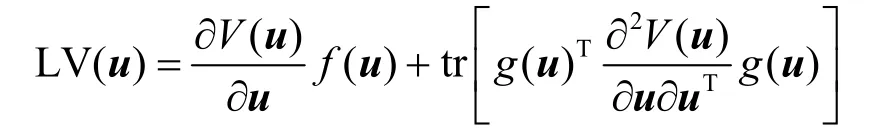
引理1 构建了一个李雅普诺夫漂移LV(u) 和式(20)中SDE 之间的一个桥梁。因此，式(20)中VSDS 的稳定性可以通过研究其李雅普诺夫漂移的特性来刻画，因此给出引理2。

引理2假设随机过程u(t) 的李雅普诺夫漂移满足如下条件

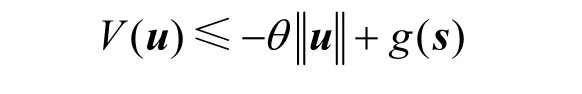
其中，θ是一个正的常量，s是一个满足如下条件的随机过程

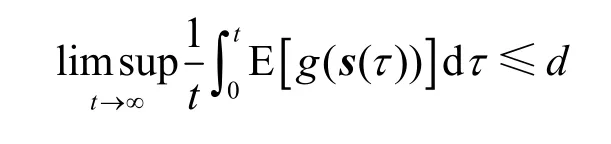
其中，d＜∞，则随机过程u(t) 一定稳定并且满足如下条件

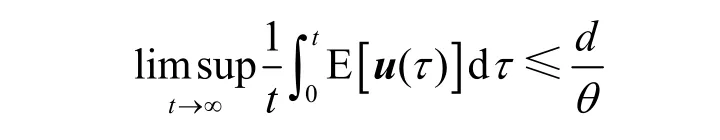
证明证明过程可参考文献[7]。

在证明VSDS 的稳定性之前给出以下假设条件。

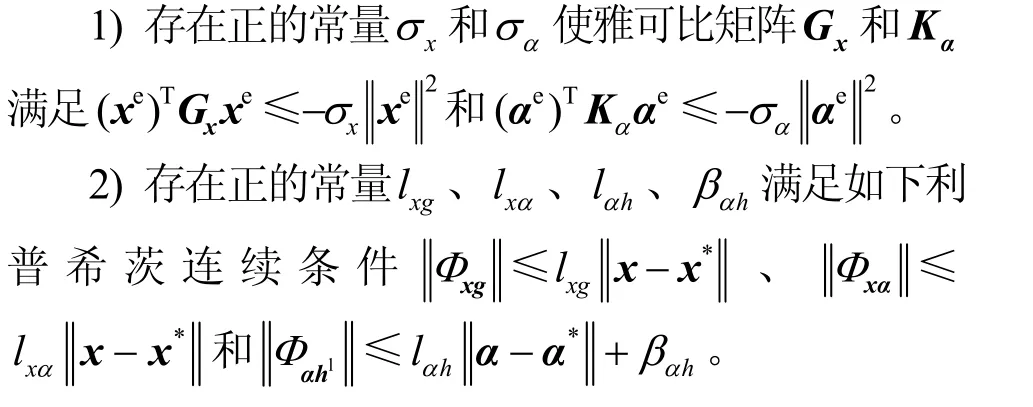
根据引理1 和假设条件，可以得到定理1。

定理1如果算法的步长因子满足条件

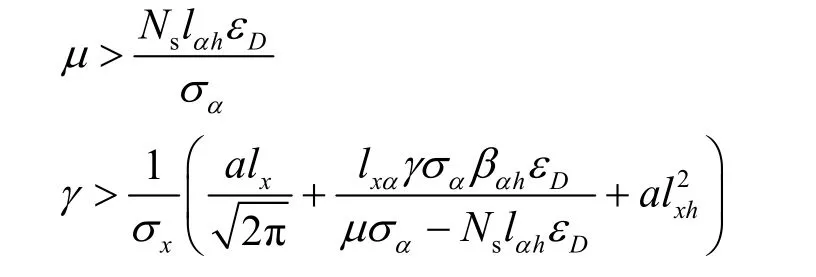
则小时间尺度迭代算法和均衡点之间的跟踪误差能够收敛到0，并且大时间尺度迭代算法和均衡点之间的跟踪误差满足上限

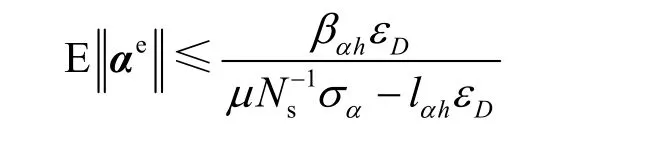
证明将大时间尺度跟踪误差αe的李雅普诺夫能量函数定义为

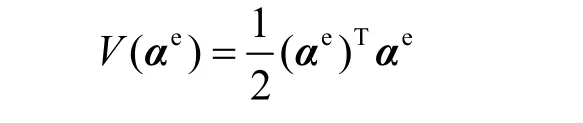
根据引理1，式(19)的李雅普诺夫漂移可以转化为

其中，c＞0 是常量。需要指出的是，上式中存在以下关系

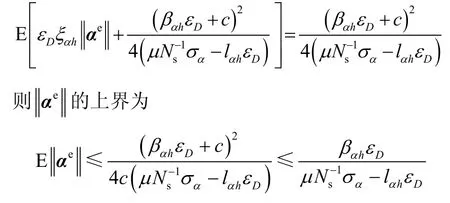
随后定义一个关于xe的李雅普诺夫函数

大时间尺度信道衰落h1和用户的位置相关，因此它的变化相对缓慢。而小时间尺度信道状态hs则变速变化，通常情况下为毫米级[8]。在相同的实数单位内，dh1的量值要比dhs小得多，因此证明中省略了dh1。根据以上结果，如果

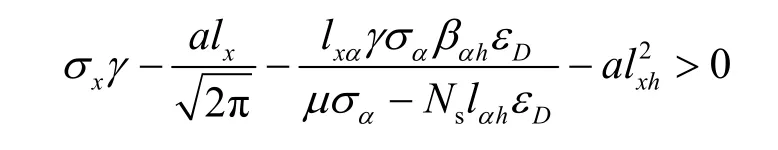
则跟踪误差xe能够收敛到0。

证毕。

在所提的双时间尺度迭代算法中，小时间尺度算法在每一个时隙需要O(1)次迭代，大时间尺度算法在每一个帧需要O(1)次迭代，则它在每一个时隙需要平均O(1/Ns)次迭代，因此算法的平均复杂度为O(1 +1/Ns)。

4 仿真分析

在仿真中，假设系统包含一个LTE 网络和2 个Wi-Fi 网络，并且每一个网络服务3 个移动终端设备。假设所有的移动终端设备采用列维行走模型在系统中随机移动[9]。所有移动设备的最大移动速度设置为vmax=2 m/s。每一个帧包含100 个时隙，即Ns=100，每个时隙为1 ms。移动设备和接入点之间的最小距离Dmin=40 m，路径损耗指数为ι=3[7]。功率增益常量G=，信道的前后时间相关性参数设置为a=0.01。w1和w2设置为0.75 和0.25。仿真中，将双时间尺度迭代算法和以下几个策略进行对比。

1) 单时间尺度最优策略[5]。在每一个时隙，单时间尺度最优策略都会描述一个和式(6)一样的频谱划分问题，并且调用一个次梯度算法来寻找当前时隙的最优解。假如单时间尺度最优策略的目标是ε-最优，即每个时隙内迭代算法的停止门限为|λ-λ*|≤ε，则单时间尺度最优策略需要在每一个时隙内进行O(1/ε2)次迭代。很明显，单时间尺度最优策略的复杂度比双时间尺度迭代算法高得多。

2) 无补偿双时间尺度策略。在无补偿双时间尺度策略中，Wi-Fi 和LTE 的频谱划分按照式(9)和式(10)分别在每个时隙和每个帧进行一次迭代。

3) 均衡点策略。均衡点策略利用次梯度迭代算法分别在每一时隙和帧找到问题式(7)和式(8)的ε-最优解。不难理解，当ε非常小时，均衡点算法得到的解可以看作双时间尺度优化问题的最优解。

图5 和图6 分别通过展示Wi-Fi 和LTE 频谱划分变量（归一化频谱）在不同时间尺度上的移动轨迹来验证基于补偿的双时间尺度迭代算法的跟踪性能。本文实验中容忍度参数被设置为一个非常小的值。因此均衡点算法的输出解可以作为最优解。从图5 和图6 可以看出，由于时变CSI 的影响，Wi-Fi 和LTE 频谱划分均衡点分别在不同的时间尺度上剧烈变化，说明无补偿双时间尺度算法很难跟踪上均衡点的动态变化。得益于式(16)和式(17)中所设计的补偿项，基于补偿的双时间尺度迭代算法能够实现对均衡点的准确跟踪。

图7 和图8 分别为加权网络吞吐量和平均迭代次数与算法容忍度ε之间的关系。通过图7 可以发现，均衡点算法总是能够获得一个和单时间尺度算法接近的网络吞吐量。然而从图8 可以看出，当ε<10-4时，单时间尺度算法所需的迭代次数比均衡点算法高得多。这验证了双时间尺度算法设计的合理性，也就是说不同的网络状态分别按不同的时间尺度变化，如果在每一个时隙上对所有的算法都进行多次迭代，则会带来大量的计算开销。从图7 可以看出，当ε比较小时，均衡点算法能够获得比基于补偿的双时间尺度迭代算法和无补偿双时间尺度算法更高的网络吞吐量；均衡点算法需要在每一个时隙内对算法进行多次迭代以获得ε-最优，这无疑会带来巨大的迭代开销。与均衡点算法不同，无论是无补偿双时间尺度算法还是基于补偿的双时间尺度算法，都只需要在每一个帧和时隙内进行一次迭代。当ε比较大时，尽管均衡点算法的迭代开销和其他算法差不多，但是其获得的网络吞吐量要比其他算法小得多。与此形成对比的是基于补偿的双时间尺度迭代算法能够在比较低的迭代开销的情况下得到较好的网络吞吐量性能。

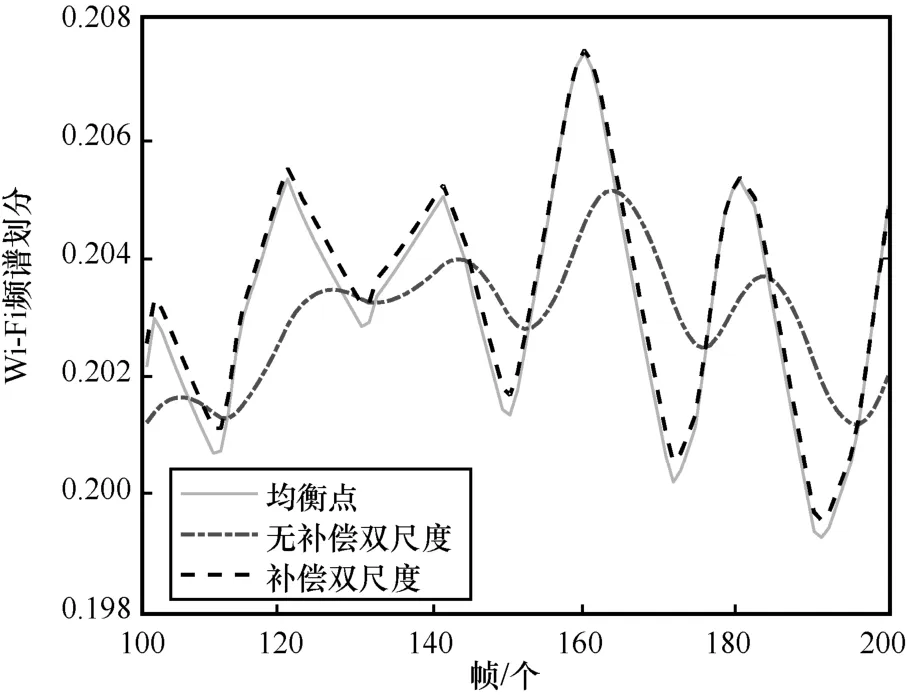
图5 Wi-Fi 频谱划分变量在大时间尺度上的移动轨迹

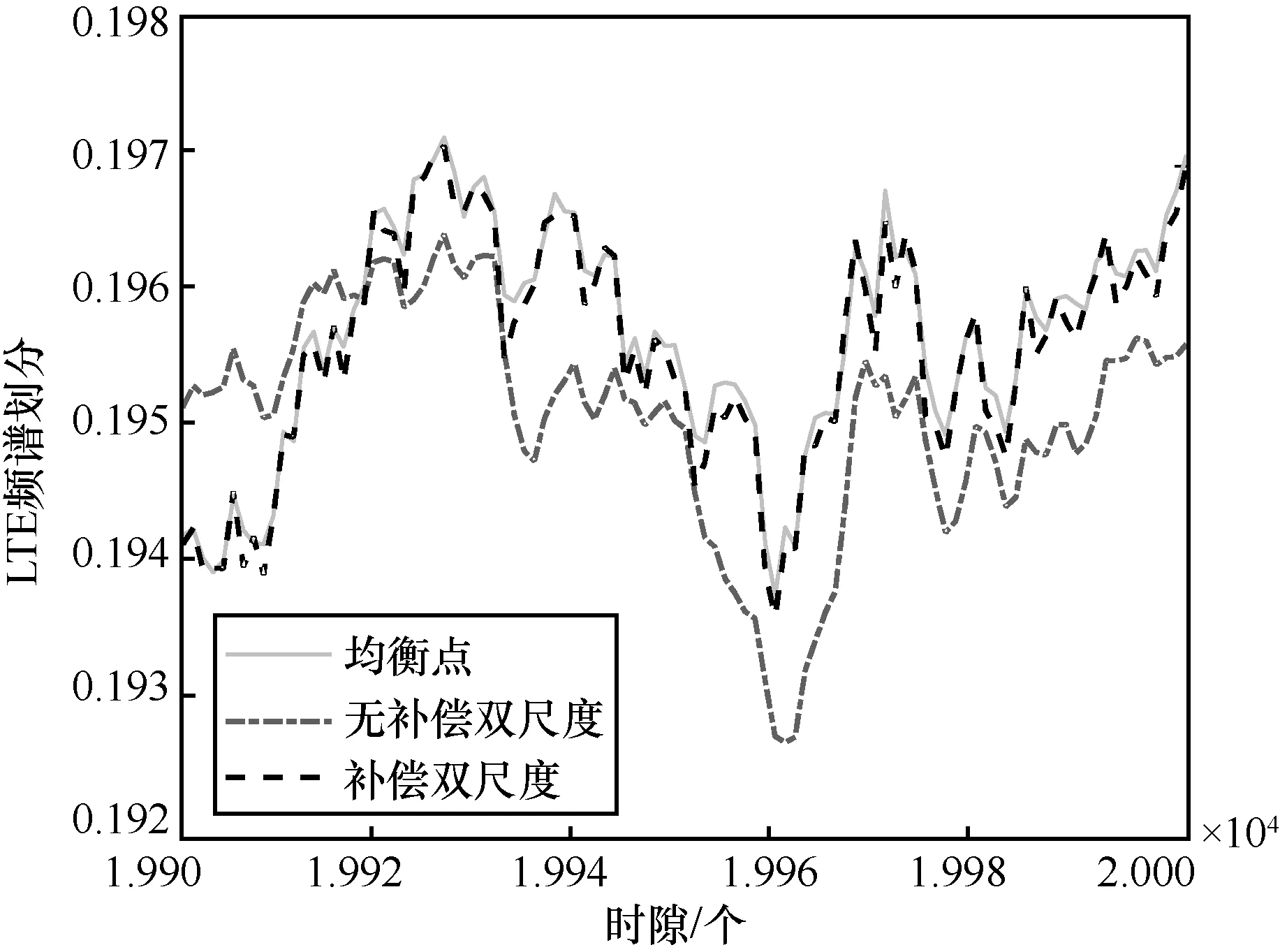
图6 LTE 频谱划分变量在小时间尺度上的移动轨迹

图9 和图10 分别为加权网络吞吐量和算法平均迭代次数与信道时间相关系数a之间的关系。从图9 可以看出，网络加权吞吐量随着a的增加而减小。这是因为a越大，无线信道的波动越大，网络传输条件越差，从而导致网络加权吞吐量越低。从图9 还可以看出，无论网络条件的好坏，基于补偿的双时间尺度算法始终能够获得比无补偿双时间算法更好的性能。虽然均衡点算法和单时间尺度最优算法能够获得比基于补偿的双时间尺度算法更好的吞吐量性能，但是从图10 可以看出，它们获得的吞吐量性能提升的代价是非常高的算法迭代开销。

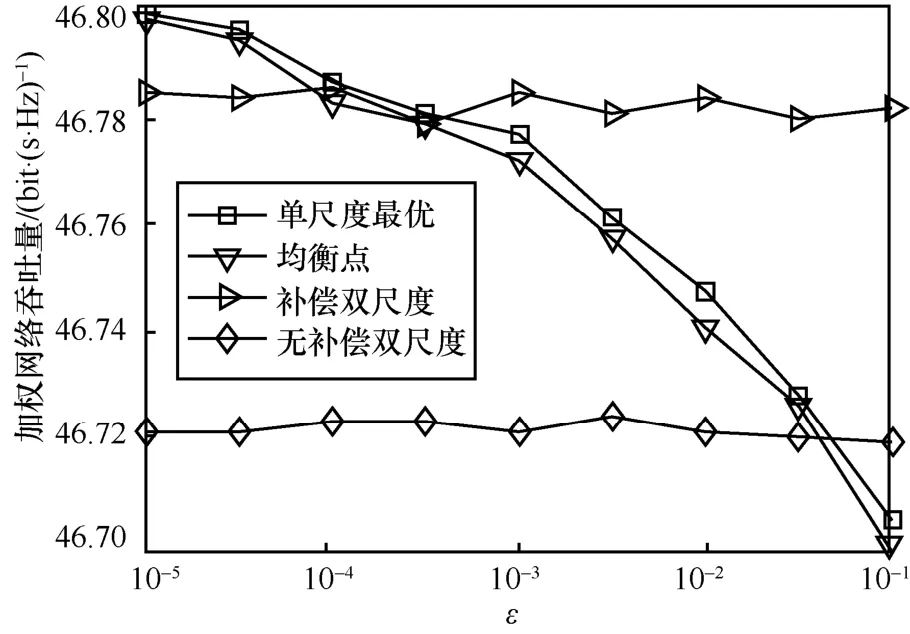
图7 加权网络吞吐量与算法容忍度之间的关系

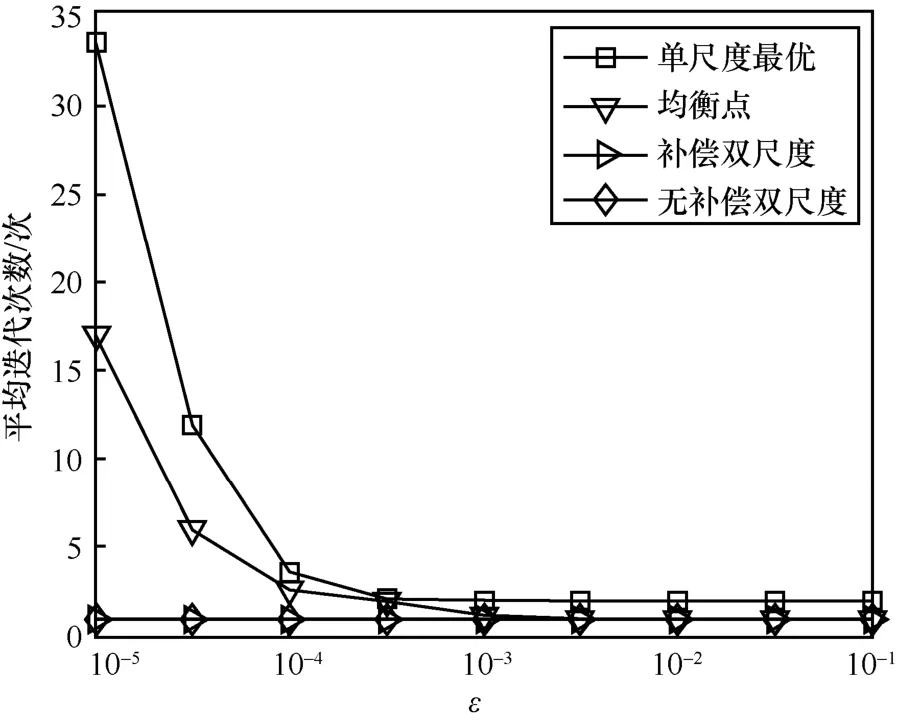
图8 平均迭代次数与算法容忍度之间的关系

5 结束语

为了实现LTE 和Wi-Fi在未授权频谱上的和谐共存，本文设计了一种基于补偿机制的双时间尺度频谱划分算法。具体而言，Wi-Fi 的频谱根据全局CSI 进行划分并且运行在以帧为单位的大时间尺度；LTE 依据局部CSI 进行频谱划分并且运行在以时隙为单位的小时间尺度。利用随机微分方程将双尺度迭代算法的跟踪误差建模为虚拟随机动态系统。最后，通过使虚拟随机动态系统稳定得到了算法收敛的充分条件。

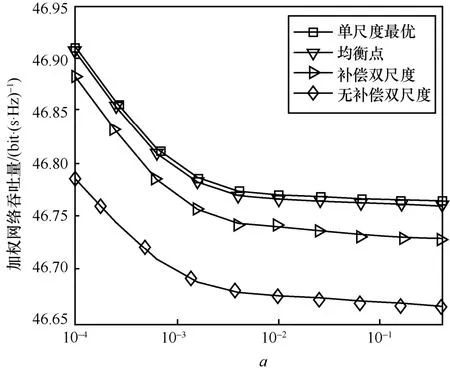
图9 加权网络吞吐量和信道时间相关系数a 的关系

图10 算法迭代次数和信道时间相关系数a 的关系