基于NTRU 的多密钥同态代理重加密方案及其应用

李瑞琪，贾春福，王雅飞

（1.南开大学网络空间安全学院，天津 300350；2.天津市网络与数据安全技术重点实验室，天津 300350）

1 引言

全同态加密（FHE,fully homomorphic encryption）是一种新型密码学原语，其支持在加密信息上进行任意函数运算，并且解密后得到的结果与在明文上执行相应运算的结果一致。同态加密的思想最初由Rivest 等[1]在1978 年提出（最初的概念被称作privacy homomorphism）。2009 年，Gentry[2-3]构造出了第一个全同态加密方案。在Gentry 的开创性工作之后，一系列关于同态加密的研究成果相继出现[4-10]。同态加密的特性使其能够广泛应用于多种云计算场景，如外包计算。

考虑如下的外包计算场景。多个数据拥有者想要联合进行某种计算（例如机器学习或数据挖掘等），于是各自将数据加密后发送到云端。云服务器在密文上进行指定的计算，然后将结果发送给接收者。接收者既可以是数据提供者，也可以是数据提供者之外的第三方。大多数情况下，数据提供者希望自己的数据对其他提供者和接收者是保密的，显然单密钥同态加密方案无法满足此要求。因此，需要一个具有如下性质的同态加密方案。1) 每个数据提供者能够用自己的公钥进行加密，并且这些密文能同时参加同态计算；2) 计算结果的接收者即使获得了（其他）数据提供者的原始密文也无法对其进行解密。

多密钥同态加密（MKHE,multi-key homomorphic encryption）支持多方用户以各自的密钥对消息进行加密，得到的密文可以一起参与同态运算。López-Alt 等[8]首次提出了MKHE 的概念并构造了第一个MKHE 方案，此后一系列MKHE 方案被提出[11-18]。MKHE 方案能够满足性质1)，并且当接收者是数据提供者时，借助于分布式解密，MKHE 方案也能够满足性质2)。然而当接收者是数据提供者之外的第三方时，只有2 种解密方式：一是把所有数据提供者的私钥收集给接收者；二是数据提供者和接收者之间进行交互。前一种情况在现实中不太可能发生，后一种情况则需要数据提供者在线才能进行解密，因此在这种场景下MKHE 的使用仍存在问题。

为了解决上述问题，Yasuda 等[19]提出了一个新概念——多密钥同态代理重加密（MKH-PRE,multi-key homomorphic proxy re-encryption ）。MKH-PRE 方案既有MKHE 的特性，也具有PRE的性质。此类方案允许数据提供者用自己的公钥加密数据来进行多密钥同态计算，同时也允许对同态计算得到的密文进行代理重加密，将结果密文转换为只能由接收者解密的新密文。重加密功能的加入使当接收者是数据提供者之外的第三方时能够满足性质2)。由于数据提供者预先生成了重加密密钥并发送到云端，因此接收者在解密时不需要与提供者进行交互，即提供者不需要实时在线。Yasuda 等[19]也给出了一个基于PS16 方案[16]的MKH-PRE 实例（简称YKHK18 方案），但该实例不适用于实际的外包计算场景，这是因为在PS16多密钥同态加密方案中，明文空间只有1 bit，大大降低了实用性；同时，PS16 方案需要在加密时生成冗余密文，给用户带来了额外的开销，并且整个方案难以实现。

NTRU（number theory research unit）是由Hoffstein、Pipher 和Silverman[20]于1998 年提出的一种基于格的公钥加密体制，此后的研究工作[21-23]构造了可证明安全的NTRU 加密方案，这些方案的安全性能够规约于标准的密码学假设RLWE（ring learning with error）。相较于传统公钥密码，NTRU具有显著的计算性能优势，而且被认为能够抵抗量子计算攻击。除此之外，NTRU 加密体制自提出后一直备受关注的原因还包括其能够用于构造具有功能性的密码学原语。近年来，一些研究关注于利用NTRU 算法构造多密钥同态加密方案[8,24-25]，但现有的NTRU 型MKHE 方案在实际应用时仍存在一定的问题。此类MKHE 方案需要将所有数据提供者的私钥收集给接收者才能解密，这意味着当接收者是数据提供者时，需要多轮协议才能完成解密；当接收者是第三方时，需要将所有私钥提供给第三方。NTRU 算法也能够用于构造代理重加密方案[26-27]，这些方案可以将密文转换成接收者能够解密的密文，因而适用于接收者为提供者之外的第三方的情况，但PRE 并不支持密文计算。综上所述，鉴于NTRU 能构造多种功能性密码学原语以及上述方案在应用中存在局限性，可以利用NTRU 算法构造适合多种外包计算场景的多密钥同态代理重加密方案。

本文构造了一个基于NTRU 的多密钥同态代理重加密方案，并给出了该方案的一个实际应用。本文主要的研究工作如下。

1) 利用密文扩张的思想设计了一种新的NTRU 型多密钥同态密文形式，并以此为基础设计了相应的同态运算和重线性化过程，从而得到了一个支持分布式解密的NTRU 型MKHE 方案。

2) 利用密钥交换的思想，在此NTRU型MKHE方案中加入了代理重加密的功能，得到了一种新的基于NTRU 的MKH-PRE 方案。新方案同时保留了MKHE 和PRE 的特性，可根据使用场景选取功能。

3) 本文方案在用户端的开销相对较低，并且支持加密多项式而不是1 bit，从而支持并行化操作，因此相较此前的MKH-PRE 方案更具实用性。

4) 将本文方案进行了实现，并应用于一个实际场景——联邦学习。实验结果表明，本文方案的使用基本不会影响联邦学习的准确性，加解密、同态运算、重加密等过程的计算开销也是可接受的。

2 基础知识

本文使用加粗大写字母表示矩阵，例如M；使用加粗小写字母表示（行）向量，例如v；v[i]表示向量v的第i个分量。对于一个实数r，表示四舍五入取整。x←D表示从分布D中随机抽取样本x。对于有限集S，U(S)表示S上的均匀分布。若一簇分布满足，则称其为B界分布。

2.1 RLWE 问题与DSPR 假设

环带错学习问题（RLWE,ring learning with error）是由Lyubashevsky 等[28]提出的。参数为n,q,χ,ς的RLWE 分布定义为：随机选取Rq中的多项式s←ς，a←U(Rq)，e←χ，输出(a,b=as+e)。判别版本的 RLWE 假设（记作DRLWEn,q,χ,ς）定义为：从RLWEn,q,χ,ς分布中抽取的多项式个样本(ai,bi)与从U(Rq)中抽取的相同个数的样本之间是统计上不可区分的。

López-Alt 等[8]介绍了判别小多项式比（DSPR,decisional small polynomial ratio）问题，其定义如下。令q为素数，φ是环R上的分布。DSPR 问题（记作DSPRq,φ）是区分如下2 个分布：1)h=gf-1的分布，其中f和g是从分布φ中随机选取的（要求f在Rq上可逆）；2)Rq上的均匀分布。

此前有关NTRU 的研究[21-23]已经证明，当分布φ为离散高斯分布Dℤn,r且时，DSPRq,φ问题是困难的（即分布1)和2)统计上不可区分），然而为了能进行多密钥同态计算，需假设当φ的标准差较小时，DSPRq,φ问题仍是困难的。

2.2 工具向量

文献[29]中介绍了工具矩阵（Gadget）G及其对应的逆函数G-1(·)。本文中，令g:=(gi)∈ℤd为工具向量，对应的分解函数为g-1:Rq→Rd。该函数将Rq中的一个元素a分解为一个向量u=(u0,…,ud-1)∈Rd，满足，并且每个ui都是小多项式。对于向量v∈，g-1(v)表示将g-1应用到v的每一个分量v[i]上，从而得到矩阵V∈Rd×d，满足gV=v(modq)。

3 多密钥同态代理重加密

本节给出多密钥同态代理重加密的形式化定义及其IND-CPA 安全性的定义。

3.1 MKH-PRE 的定义

令M 为明文空间，设每个参与同态运算的用户都有一个id，每个同态密文都伴随着一个用户id集合，用来记录计算过程中涉及的所有用户。“新鲜的”密文所对应的集合T中只包含一个元素，即T={id}，而经过多密钥同态运算后的密文对应的集合会变为T={id1,id2,…,idk}。一个多密钥同态代理重加密方案包括如下算法。

pp ←Setup(1λ)：输入安全参数λ，输出公共参数pp。

(pk,sk) ←KeyGen(pp)：输入公共参数pp，输出公钥pk 和私钥sk。

c←Enc(pk,m)：输入消息明文m∈M 和公钥pk，输出密文c。

一个MKH-PRE 方案应当满足以下性质。

正确性。令c1,…,cs为密文，mi为ci对应的明文，{skid}id∈Ti为ci对应的私钥。令 C:Ms→M 为作用于m1,…,ms的电路，cEval为同态计算电路C 后得到的密文。令rk 为重加密密钥，cReEnc为对cEval重加密后得到的密文，其对应的私钥为skj。若

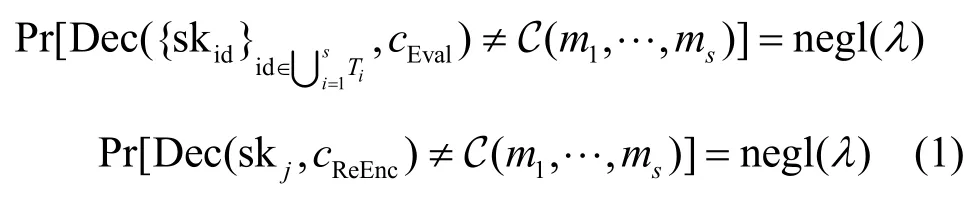
成立，则称该MKH-PRE 方案是正确的。

紧致性。若存在一个多项式poly(·,·) 使一个对应N个用户的密文cEval及其重加密后得到的密文cReEnc的尺寸满足|cEval| 和|cReEnc|都小于poly(λ,N)，则称该MKH-PRE 方案是满足紧致性的。

3.2 安全性定义

本文采用的是文献[21]中关于MKH-PRE 方案的安全性定义。该定义中设计了一个敌手A 与挑战者之间的IND-CPA 安全游戏，使用一个有向非循环图来记录重加密过程，图中的顶点表示诚实用户，边表示可能的重加密方向。在此游戏中，敌手能够根据重加密图的情况来发起重加密密钥生成的询问。敌手和挑战者之间的IND-CPA 安全游戏的形式化定义如下。

阶段1

准备挑战者将pp ←Setup(1λ)发送给A。令E=∅为重加密图的边的集合。

诚实密钥生成A 将诚实密钥的数量NU发送给挑战者，挑战者生成(pki,ski),i=1,…,NU并将pki发送给A。令ΓH为诚实公钥集合。

非诚实密钥生成A 将非诚实密钥的数量NC发送给挑战者，挑战者生成(pki,ski),i=1,…,NC并将其发送给A。令ΓC为非诚实公钥集合。

阶段2

A 可以以任意顺序发起多项式个询问。

重加密密钥生成A 将(i,j)发送给挑战者。若i,j∈ΓH且G=(ΓH,E∪(i,j))是有向非循环图，挑战 者 将 (i,j)添 加 到E中 并 将rki→j←RKGen(ski,pkj)发给A；否则返回⊥。

重加密A 将 (i1,…,is,j,c)发送给挑战者。若j∈ΓC且c=c*，挑战者返回⊥；否则挑战者将cj←ReEnc(rki1→j,…,rkis→j,c)发送给A，其中rkik→j←RKGen(skik,pkj),k=1,…,s。

阶段3

A 输出一个比特b' ∈{0,1}。

在此游戏中，敌手A 的优势定义为

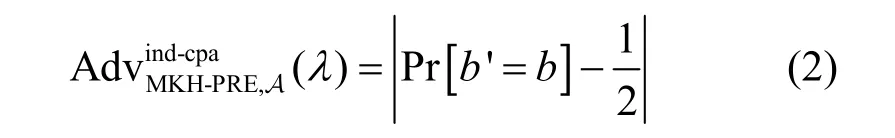
若对于任意概率多项式时间的敌手A 有

成立，则称该MKH-PRE 方案是IND-CPA 安全的。

4 方案构造

本节介绍基于NTRU 的多密钥同态代理重加密方案的构造。首先介绍Setup 和KeyGen 这2 个算法，这是整个方案的基础。

Setup(1)λ。输入安全参数λ，生成RLWE 的维数n、密文模数q、明文模数t和R上的分布ψ,χ；随机抽取向量a←U()和矩阵A←U()；输出公共参数pp=(n,q,t,ψ,χ,a,A) 。

KeyGen(pp) 。随机抽取f',g←ψ，计算f=tf'+1(modq)，若f在Rq中不可逆，则重新抽取f'。计算f-1∈Rq并设h=tgf-1(modq)。随机抽取误差向量e←χd，计算b=-a f+e(modq)。令f=(f,1)∈，随机抽取误差向量e'←χn'，计算d=-fA+e' (modq)∈。输出公钥pk=(h,b,d)和私钥sk=f。

4.1 多密钥同态加密的构造

本节介绍多密钥同态加密部分的算法。类似于文献[30-31]，本文使用的是Regev 型的NTRU 算法。本节除了给出前文所介绍的Enc、Dec 和Eval 算法之外，还将介绍EvkGen、CtxtExtend 和Relin 算法，这些算法是多密钥同态加密的重要组成部分。

南水北调受水区地下水压采工作面临的问题与对策………………………………… 韩小虎，刘昀竺，姚文锋(22.23)

重线性化。在同态乘法运算的过程中，需要对密文进行重线性化。算法过程如下。

算法1重线性化算法Relin

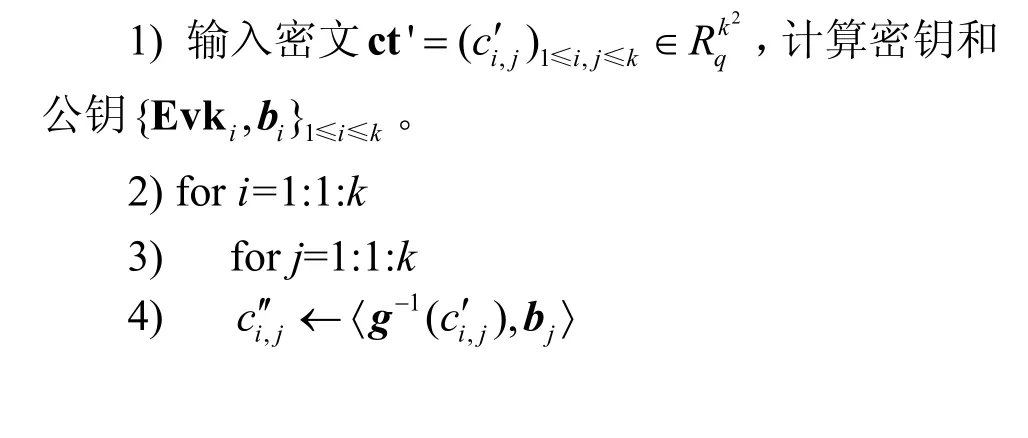
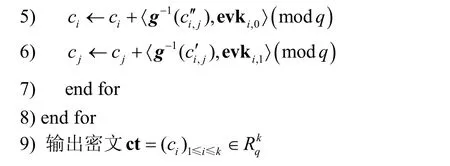
下面，说明重线性化算法的正确性。已知用户i生成的计算密钥Evki为

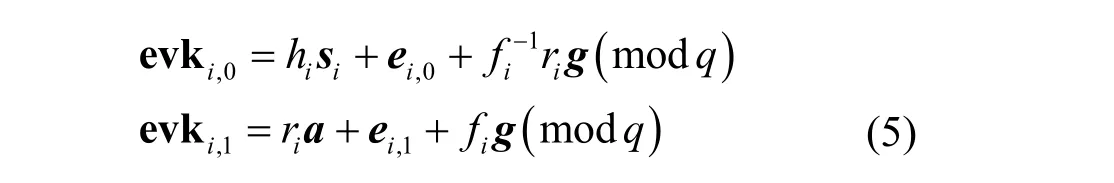
根据式(5)可得

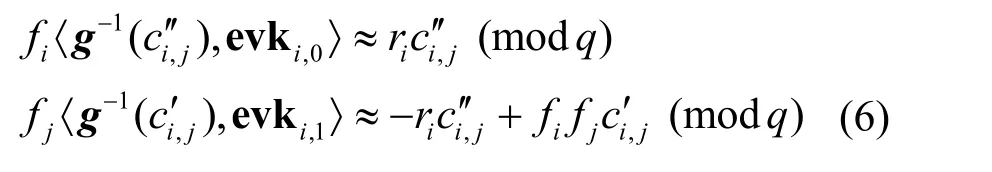
所以有

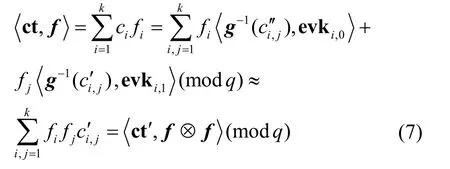
因此，重线性化过程是正确的。注意到，重线性化过程中需要用公钥加密其对应的私钥，因此需假设本文方案具有循环安全性。

4.2 分布式解密

在4.1 节介绍的多密钥同态加密方案中，解密多密钥密文需要所有参与运算的用户的私钥作为解密算法的输入。然而在实际应用中，某一方（运算参与方或第三方接收者）拥有所有私钥是不合理的。因此，可以设计一个协议进行分布式解密。本文方案利用一个简单且直接的方式——噪声泛洪[32-33]，来实现分布式解密。

分布式解密由 2 个算法组成：PartDec 和FinDec。在PartDec 算法中，用户id 为i的运算参与方接收到多密钥密文ct 的第i个分量ci后，用自己的私钥fi将其解密并加上随机抽取的噪声←φ（噪声分布φ的标准差远大于噪声分布χ的标准差）。在FinDec 算法中，所有用户将自己的部分解密结果广播给其他用户，每个用户接收到所有其他用户的部分解密结果后，将其合并起来以恢复明文。

PartDec(ci,fi)。输入分量ci和密钥fi，随机抽取，计算并输出ρi=f i ci+。

4.3 代理重加密

本节介绍重加密密钥生成算法RKGen、重加密算法ReEnc 及其对应的解密算法PRDec。

于是，每个重加密密钥RKi→j满足

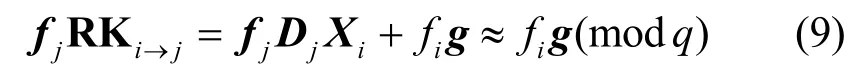
因此，调用PRDec(skj,c')的计算结果满足

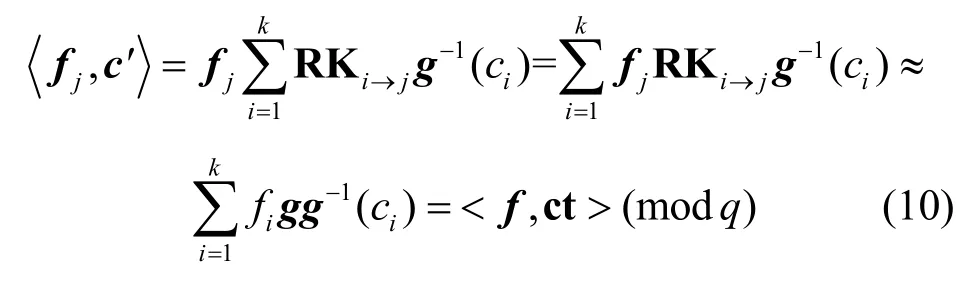
因此，重加密过程是正确的。

5 方案分析

5.1 噪声分析

本节对同态运算过程和代理重加密过程中的噪声变化问题进行分析。首先，对密文的噪声进行定义。令ct∈为一个多密钥密文，其对应的明文为m∈Rt，对应的私钥为f∈。若存在e∈R使〈ct,f〉=Δm+e(modq)，则称e是密文ct 的噪声。为了保证密文能够被正确解密，该密文的噪声需要满足。设方案中使用的分布ψ是Bkey界分布，χ是Bχ界分布，函数g-1(·)输出向量的无穷范数的上界为Bg。

显而易见，同态加法使噪声线性增长，因此重点关注同态乘法和代理重加密对噪声的影响。

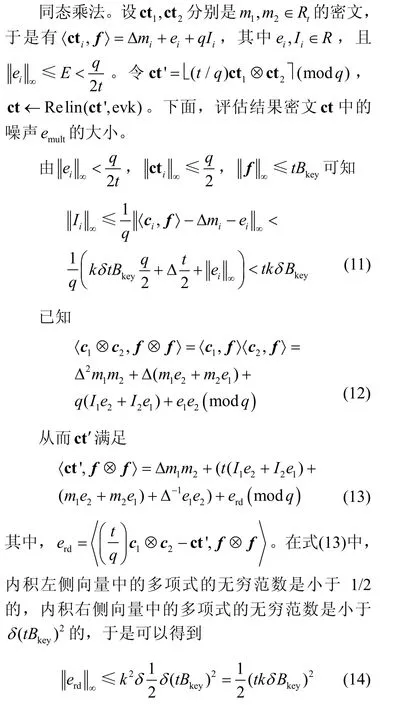
因此，ct' 的噪声上界为

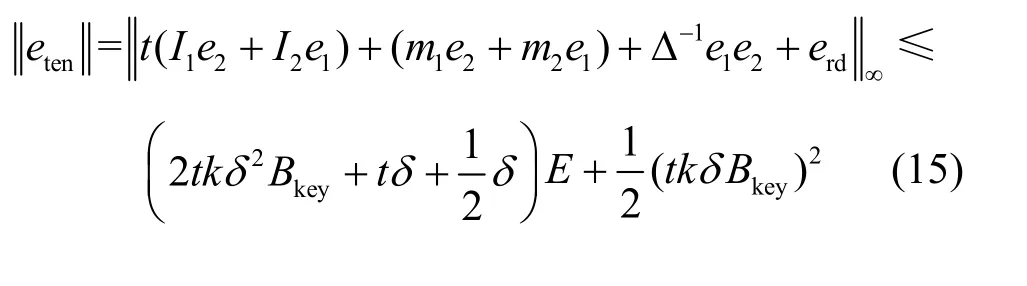
下面，评估ct←Relin(c t',evk)过程中密文噪声的变化情况。根据算法1 可知

综上所述，进行一次同态乘法后，密文噪声的上界为

5.2 安全性分析

首先，说明MKHE 方案的安全性。考虑由公钥和密文向量中的一个元素组成的二元组(hi,ci=hi s+e+Δm)。若hi是从Rq上的均匀分布中选取的，并且s←ς,e←χ，那么此时(hi,ci)可以看成是从RLWE 分布中选取的。因此需要保证选取的g和f能够使h=pgf-1的分布与U(Rq)是统计意义上接近的。此前相关研究[11-12,27-28]已经证明，当选取g和f的分布为离散高斯分布且标准差大于时，DSPRq,φ问题是困难的。然而为了保证解密正确性，需要将标准差设为较小的值（即需要DSPR假设）。尽管DSPR 假设未被证明是困难的，但是当q=2nε,ε∈(0,0.5)时，仍然没有高效的方法去攻破DSPR 假设[34]。因此，若RLWE 假设、DSPR 假设和循环安全假设是困难的，则本文的MKHE 方案是IND-CPA 安全的。

然后，考虑PRE 过程的安全性。令A 为任意一个概率多项式时间的敌手，其能够访问重加密密钥生成预言机RKGen 和重加密预言机ReEnc，但只能够根据重加密图来发起重加密密钥生成的询问。考虑如下的一系列安全游戏。

Game 0。此游戏就是3.2 节中定义的IND-CPA安全游戏。假设ΓH={1,…,N}，ΓC={N+1,…,M}。令1,…,N是由重加密图确定的拓扑顺序，即若i＜j则不存在从i到j的边。也就是说，A 只能发起生成满足i＞j的重加密密钥rki→j的询问。

将Gamek,k=1,…,N分为2 类，Gamek.1 和Gamek.2，并且令Game 0.2 即为Game 0。

Gamek.1。除了当A 发起生成诚实密钥的询问时，对于所有的i＜k，挑战者通过随机抽取hi←U(Rq)和di←U(Rqn')来生成公钥；对于所有的k＜i≤N，挑战者计算公钥(hi,di)←KeyGen(pp)，其余操作与Gamek-1.2 相同。

Gamek.2。除了当A 发起生成重加密密钥的询问时，对于所有的j＜i≤k，挑战者通过从中随机抽取矩阵来生成重加密密钥rki→j；对于所有的k＜i,j≤N，挑战者计算rki→j←RKGen(ski,p kj)，其余操作与Gamek.2 相同。

Game final。除了当A 发起挑战询问时，挑战者通过随机抽取来生成密文c，其余操作与GameN.2 相同。

敌手A 在Gamei中的优势记作(λ)。下面，评估A 在每个游戏中的优势。

由于Game 0 是原始的MKH-PRE 方案的IND-CPA 游戏，因此有

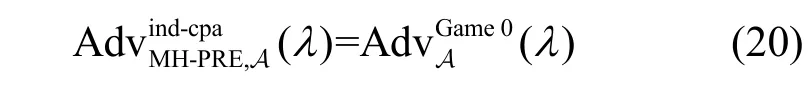
利用敌手A 构造一个PPT 算法B，用来区分RLWE 分布与均匀分布。向B 输入的样本x∈R2要么来自RLWE 分布（其秘密多项式为f），要么来自均匀分布。

阶段1

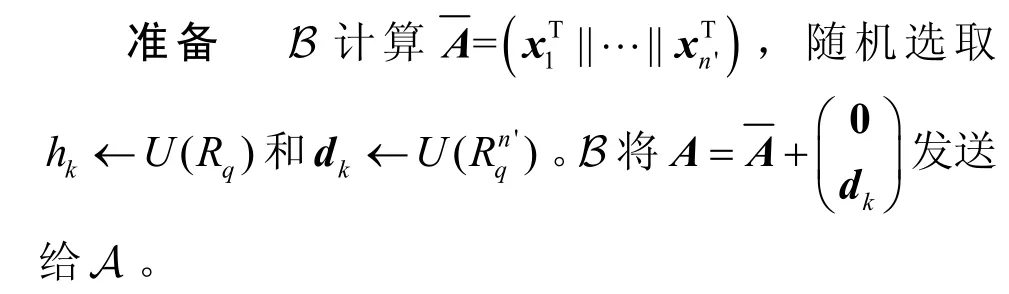
诚实密钥生成当A 发起一个生成诚实密钥的询问时，B 的应答如下。

非诚实密钥生成当A 发起一个生成非诚实密钥的询问时，B 计算(pki,ski) ←KeyGen(A) 并将(pki,ski)发送给A。

阶段2

重加密密钥生成当A 发起一个生成重加密密钥的询问(i,j)时，若i,j＜k，则B 返回一个从均匀分布中随机抽取的；若i,j＞k，则B返回RKi→j←RKGen(ski,pkj)。

阶段3

当A 停止询问并输出比特b' ∈{0,1}时，若b=b'，则B 输出1；否则输出0。

如果向B 输入的分布是RLWE 分布，那么可以发现B 模拟了Gamek-1.2。的第一行和dk都是服从均匀分布的随机量，因此A也是服从均匀分布的。另外，dk≈-(f||1)A的分布与实际游戏中的相同。由于在先前的游戏中rki→j被替换成了从均匀分布中随机抽取的矩阵，因此B 完全模拟了Gamek-1.2。相反地，如果向B 输入的是均匀分布，显然B 模拟了Gamek.1。因此根据上述讨论、RLWE 假设和DSPR 假设可知

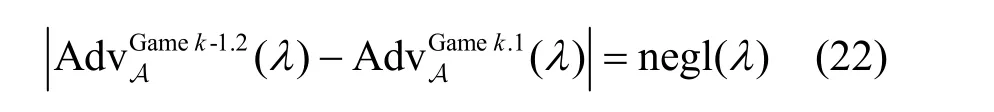
在Game final 中，密文是从均匀分布中随机抽取的；在GameN.2 中，所有的公钥在前面的游戏中都被替换成了从均匀分布中随机抽取的向量，从而根据RLWE 假设，加密算法输出的密文与从均匀分布中随机抽取的多项式是统计不可区分的。因此GameN.2 与Game final 是统计上不可区分的，即

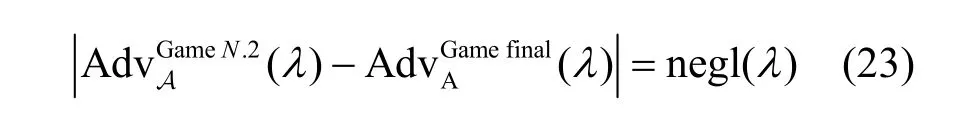
B 在Game final 中的优势为

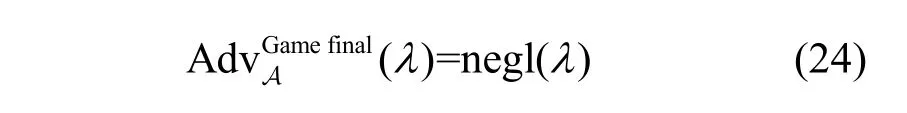
因此，根据上述分析可以得出

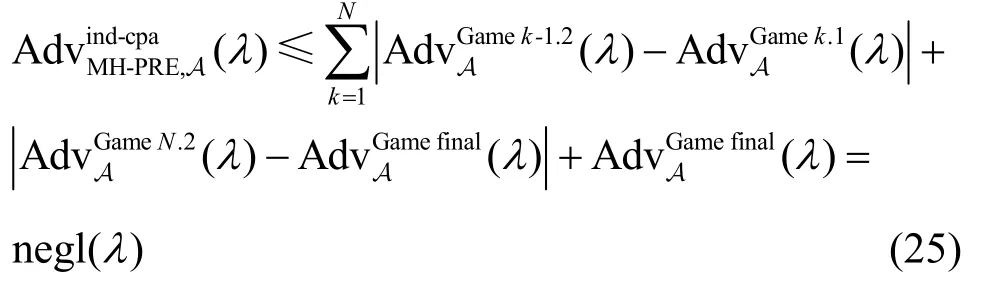
因为敌手A 的选取是任意的，所以本文方案是IND-CPA 安全的。

5.3 性能分析

本节讨论MKH-PRE 方案的计算开销和空间开销，并假设某次同态运算中有k个用户参与。

首先，考虑空间开销。一个多密钥密文由k个多项式组成；进行同态乘法共需k个计算密钥，每个计算密钥由2d个多项式组成；进行代理重加密时同样需要k个重加密密钥，每个重加密密钥由2d个多项式组成。因此，同态计算中的密文尺寸为O(knlogq)，单个用户生成的计算密钥尺寸为O(dnlogq)，重加密密钥尺寸为O(dnlogq)。

然后，考虑计算开销，主要考虑同态乘法和重加密过程的开销。计算过程中多项式乘法在总开销中占主导地位，因此主要统计每个算法需要进行的多项式乘法的次数。在同态乘法中，计算张量积需要k2次多项式乘法。算法1中的一次迭代则需要3d次多项式乘法，因此运行一次算法1 需要3kd次多项式乘法。重加密过程需要2kd次多项式乘法。

5.4 方案对比

本节将给出本文方案与相关方案的对比。

1) 与LTV12 方案的对比

表1 中列出了本文方案与LTV12方案[8]的一些基本性质之间的对比，其中n表示分圆多项式的次数，q表示模数，d表示工具向量的维数。第二行中的“（用户）”是指单个用户所需生成的计算密钥的尺寸。

从表1 中可以看出，本文方案中用户所需生成的计算密钥相对较小，因此用户端的开销也会相对较低。同时，本文方案中的MKHE 部分支持分布式解密，从而可以构造一个2 轮的安全多方计算协议，而LTV12 方案并不支持；另外，本文方案还具有代理重加密功能。

2) 与YKHK18 方案的对比

表2 中列出了本文方案与YKHK18 方案[19]的一些基本性质之间的对比，其中λ表示安全参数，L表示方案能够同态运行的电路的最大层数，K表示预先设定的最大用户数上限，k表示当前参与运算的用户数量，t表示当前参与运算的密文数量，(·)表示省略对数项。文献[35-36]提出的对于NTRU 型方案的攻击手段的复杂度为，其中n为多项式次数，q为模数。为了保证安全性，攻击成功的时间需要大于2λ，于是有n＞(λ2log2q)。另外，为了能够进行L层同态运算，需满足logq＞(L)。

从表2 中可以看出，本文方案的明文空间更大，能够支持批处理操作，因而更适合于实际应用。同时，虽然YKHK18 方案不需要生成计算密钥，但是其需要生成冗余密文来辅助多密钥同态运算。因此，综合用户端通过计算生成的公钥、计算密钥、重加密密钥的尺寸以及明密文的尺寸比例来看，相较于YKHK18 方案，本文方案用户端开销相对较低。

6 在联邦学习隐私保护中的应用

本节将给出本文方案在一类典型的多方云计算场景——联邦学习中的应用。

6.1 联邦学习及其隐私保护

联邦学习是一种机器学习框架，由多个数据所有者和云服务器组成，拥有不同训练数据集的多个训练参与者共同执行一个学习任务。每个数据所有者事先约定好模型初始参数，首先在本地训练模型，然后将模型参数上传至云服务器。云服务器在收集所有参与训练方的模型参数后对其进行处理，更新全局模型参数并发送给训练参与方。不断重复上述过程，直至模型收敛。联邦学习环境可以实现数据所有者在不需要给出己方数据的情况下，能够协同其他数据所有者共同训练模型。

联邦学习的训练过程中权重参数的传输会存在隐私安全问题，因此需要建立隐私保护机制。将权重参数进行加密处理能够实现权重参数的保密，但各个训练参与方若使用同一对公私钥，则需要共享密钥。如果密钥被窃取，整个系统的安全性将遭到破坏。在这一场景下，多密钥同态加密方案能够提供更好的安全性，每个参与者可以直接使用自己的公钥进行加密操作，不需要执行共享密钥的协议，进而降低了密钥被窃取的风险。

表1 本文方案与LTV12 方案的对比

表2 本文方案与YKHK18 方案的对比

6.2 模型设计

本文设计了2 种联邦训练卷积神经网络的场景，分别是联邦卷积神经网络场景和代理重加密-联邦卷积神经网络场景。在这2 种场景中，云服务器都是诚实且好奇的。联邦卷积神经网络场景如图1 所示。每个训练参与方使用自己的公钥将自己的模型参数iw加密后上传到云服务器；云服务器对参数进行处理，然后将更新后的全局参数发送给参与者；参与者解密参数后更新自己的模型并进行下一轮迭代。重复上述步骤，可以实现多方共同训练一个神经网络模型，同时训练者无法获知其他训练者的模型参数。

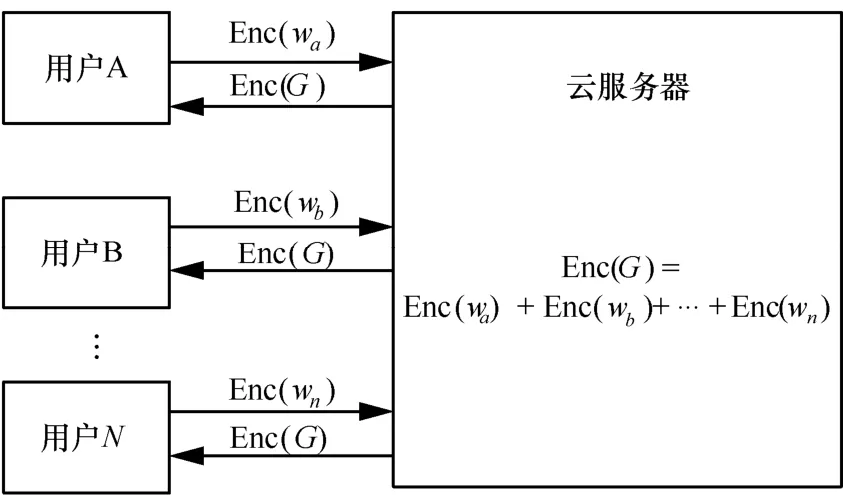
图1 联邦卷积神经网络场景

代理重加密-联邦卷积神经网络场景如图2 所示。与联邦卷积神经网络场景的不同之处在于，模型接收者并不存在于模型训练者之中。此时，需要重加密机制将密文转换为接收者可以解密的密文。在此场景中，需假设云服务器不能与用户K共谋。

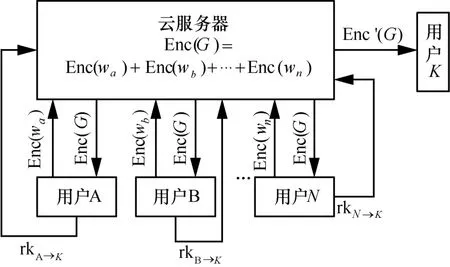
图2 代理重加密-联邦卷积神经网络场景

6.3 实验与分析

本实验使用的配置为：Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz 3.41 GHz，16 GB 内存。在虚拟机中使用Ubuntu16.04 系统和C++语言，借助GMP 库和NTL 库实现MKH-PRE 方案；使用Python 语言实现联邦学习过程。实验选取的具体场景为3 个参与方在联邦学习框架下通过一个云服务器共同训练卷积神经网络。选取的卷积神经网络包含四层结构，分别是卷积层、非线性层、池化层和全连接层，非线性层选取ReLU函数，全连接层选取softmax 激活函数。实验使用的数据集为cifar-10，训练集包含55 000 个样本，其中参与者A 有20 000 个样本，参与者B 有20 000 个样本，参与者C 有15 000 个样本；测试集包含5 000 个样本。

本文采用的对照实验如下。1) 使用明文参数直接进行联邦学习，迭代30 000 次。2) 参与者使用自己的公钥对权重参数进行加密，云服务器每一轮收集3 个密文参数并进行聚合，将计算得到的全局参数密文发送给训练参与者，参与者解密后进行下一轮训练；重复此过程进行联邦学习，其余参数设定与1)相同。两组实验得到的训练集准确率如图3 所示，其中横坐标表示迭代次数（坐标间隔为1 000），纵坐标表示准确率。图3(a)为明文参数下的训练集准确率随迭代次数变化的曲线，图3(b)为密文参数下训练集准确率随迭代次数变化的曲线，两组实验得到的准确率变化趋势基本一致，说明同态加密过程几乎不影响训练过程。

两组实验的测试集准确率如表3 所示，表3 中的准确率为多次实验后的平均值。从表3 中可以看出，明密文参数模型下的测试集准确率几乎一致，说明同态加密过程基本不影响模型的准确性。

本文也进行了代理重加密过程的实验。云服务器使用训练参与方生成的重加密密钥将多密钥同态计算得到的模型参数密文进行重加密，所得结果发送给用户K。用户K使用自己的私钥将模型参数解密，得到训练好的模型。实验结果表明用户K的测试集准确率约为70.83%，与表3 中准确率几乎一致，这说明重加密过程基本不影响模型的准确性。上述结果表明本文所提的MKH-PRE 方案并没有使训练过程和训练结果（获得的模型）产生偏差。

本文也对MKH-PRE 方案的各个算法的运行时间进行了测试。多密钥同态加密过程中各个算法的运行时间如表4 所示，代理重加密过程中各个算法的运行时间如表5 所示。由表4 和表5 的实验结果可知，本文方案具有良好的时间效率。

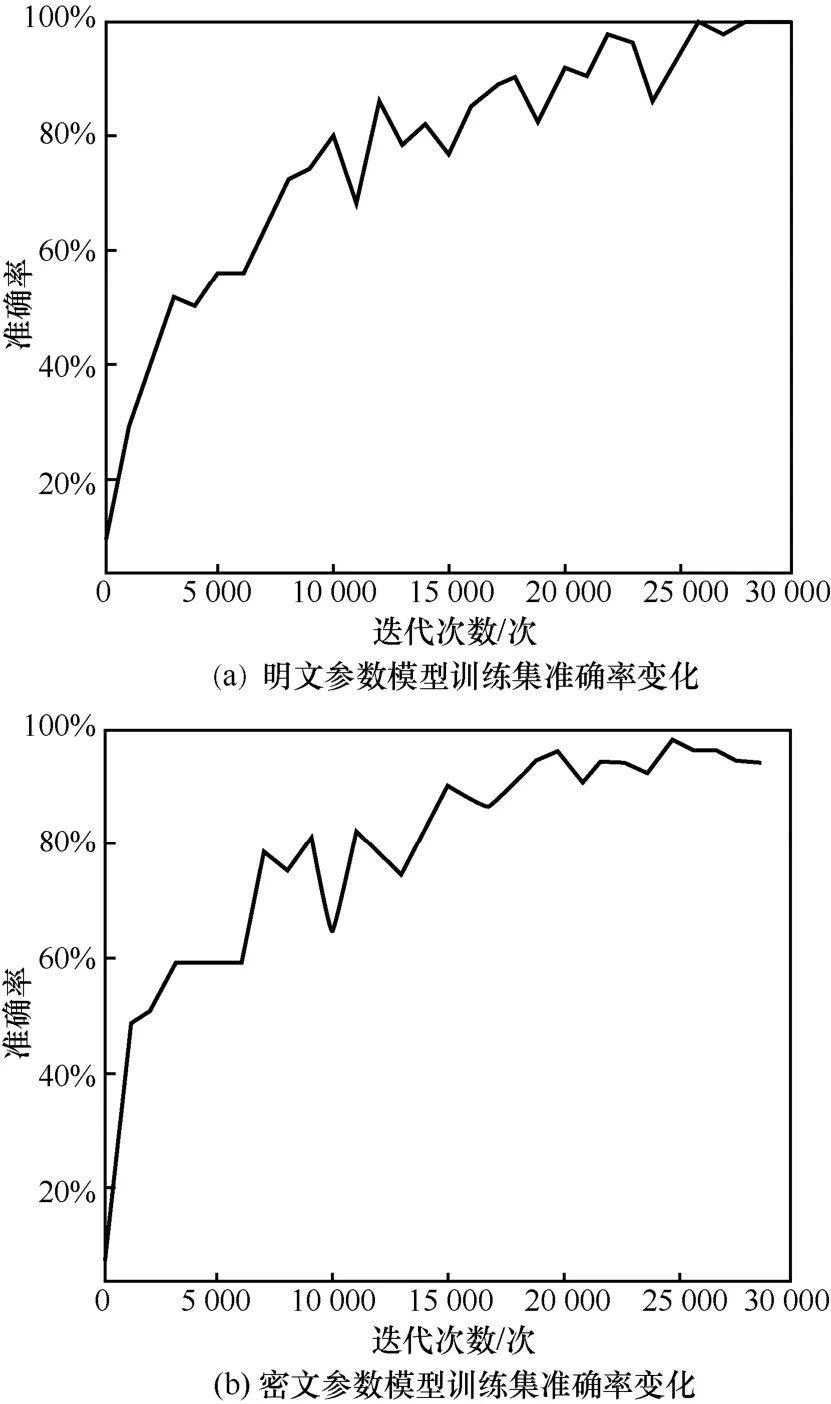
图3 训练集准确率变化

表3 明密文参数模型下的测试集准确率

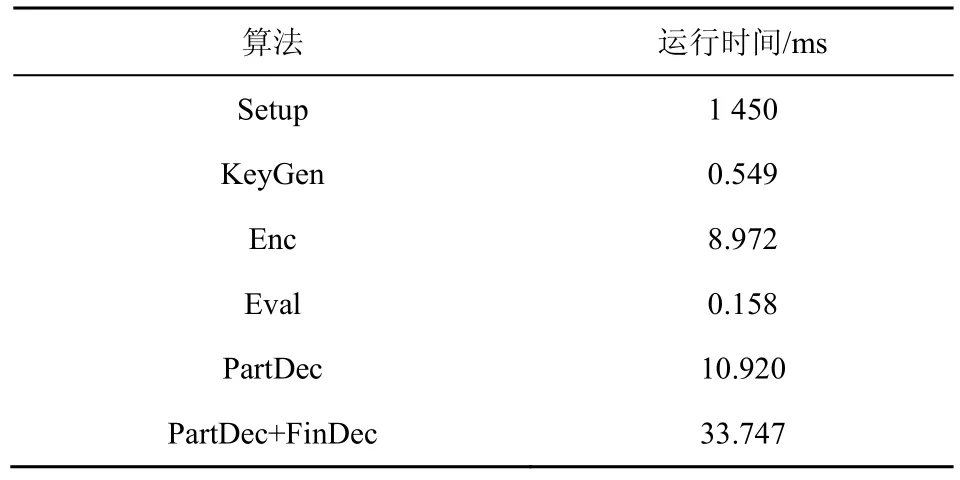
表4 多密钥同态加密过程中各个算法的时间开销

表5 代理重加密过程中各个算法时间开销

7 结束语

本文提出了一种基于NTRU 的多密钥同态代理重加密方案。该方案同时保留了多密钥同态加密和代理重加密的特性：多密钥同态加密功能支持分布式解密，适用于数据提供者是接收者的安全多方计算场景；代理重加密功能适用于接收者为数据提供者之外的第三方的外包计算场景，使用者可以根据具体场景需求选择合适的功能。另外，本文方案支持加密多项式环中的元素，用户端的开销也相对较小，因而相较于此前的MKH-PRE 方案更具实用性。最后，将本文方案进行了实现并应用于联邦学习场景以解决其中的隐私保护问题。实验结果表明，本文方案几乎不影响联邦学习的准确率，也不会带来较大的计算开销。