时间尺度上完整非保守力学系统的Noether定理
2020-04-13张毅
张 毅
(苏州科技大学 土木工程学院,江苏 苏州215011)
时间尺度是实数集的任意非空闭子集。 时间尺度上微积分将微分方程和差分方程的研究统一并推广到时间尺度动力学方程的框架下进行,不仅避免了对微分方程和差分方程的重复研究,而且可以更深刻地揭示连续系统、离散系统以及其他复杂系统动力学的本质差异。 自1988 年德国学者Hilger 在其博士论文基础上建立时间尺度分析理论以来,已经在科学和工程的诸多领域得到了广泛应用[1-3]。 2004 年,Bohner[4]、Hilscher和Zeidan[5]研究了时间尺度上变分问题。2008 年,Bartosiewicz 和Torres[6]首先建立了时间尺度上Noether 定理并利用时间重新参数化方法给出了定理的证明。 此后,Bartosiewicz 和Torres 等[7]导出了时间尺度上变分问题的第二Euler-Lagrange 方程,并基于该方程给出了Noether 定理的另一证明。时间尺度上动力学及其Noether定理是对经典连续版本和离散版本动力学及其Noether 定理的统一和推广,近年来引起人们的广泛关注[8-17]。文章将进一步研究时间尺度上完整非保守力学系统的Noether 对称性与守恒量, 建立系统的Noether 定理,并给出定理的一个直接证明。
1 时间尺度预备知识
时间尺度是实数集R 的任意非空闭子集,通常用T 表示。例如,实数集R、整数集Z、自然数集N,或[1,2]{3,4,5}等都是时间尺度,而有理数集Q、复数集C,或者开区间(0,1)等都不是时间尺度。
研究时间尺度时,向后跳跃算子 ρ:T→T 和向前跳跃算子 σ:T→T 起着核心作用,其定义为 ρ(t)=sup{s∈T:s<t}和 σ(t)=inf{s∈T:s>t}。 如果 ρ(t)=t,ρ(t)<t,σ(t)=t,以及 σ(t)>t,则点 t∈T 分别称为左稠密、左发散、右稠密和右发散的。 由 μ(t)=σ(t)-t 定义的函数 μ:T→R+称为向前步差函数。
设函数 f:T→R,t∈Tk,其中 Tk=T(ρ(supT),supT],则 f 在 t 的 Δ-导数 fΔ(t)定义为:给定任意 ε>0,存在δ>0,使得 t 在的邻域 U=(t-δ,t+δ)∩T 上对所有 s∈U 成立|f(σ(t))-f(s)-fΔ(t)(σ(t)-s)|≤ε|σ(t)-s|。 如果对所有的 t∈Tk,fΔ(t)存在,则称 f在 Tk上是 Δ-可微的。 fΔ(t)也可表示为(Δ/Δt)f(t)。
如果函数f:T→R 在时间尺度T 中的每个右稠密点连续,且在每个左稠密点具有左极限,则称函数f 是rd 连续的。 用记号分别表示在T 上所有rd 连续的函数的集合以及在Tk上具有rd 连续的Δ-导数的Δ-可微函数的集合。
如果对所有的 t∈Tk,有 FΔ(t)=f(t),则函数 F:T→R 称为函数 f:T→R 的一个原函数。 函数 f 的不定积分定义为定积分定义为其中 a,b∈T,C 是任意常数。
对于 Δ-可微函数 f(t)和 g(t),以下公式成立[1]
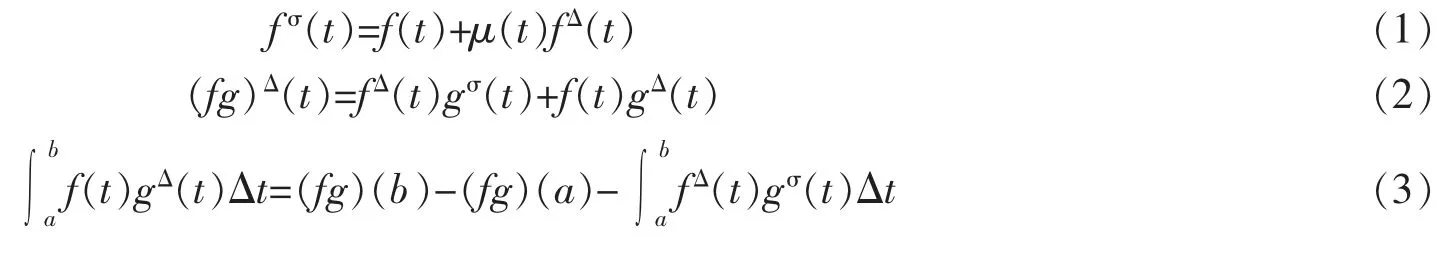
其中 fσ(t)=f(σ(t)),即 fσ=f ◦σ。
时间尺度上 Dubois-Reymond 引理[1]:令则当且仅当 g(t)≡C 时,其中 t∈[a,b]k,常数C∈Rn,对所有且
关于时间尺度上微积分更详细的介绍可参阅Bohner 和Peterson 的著作[1]。
2 时间尺度上非保守系统的Hamilton原理和Lagrange方程
时间尺度上Hamilton 作用量为

其中 qsσ(t)=(qs◦σ)(t),qsΔ(t)是广义坐标 qs对 t 的 Δ-导数;L:R×Rn×Rn→R 是 Lagrange 函数。 假设这些函数都是函数,s=1,2,…,n。
时间尺度上Hamilton 原理为


且满足互易关系

以及端点条件

原理(6)可称为时间尺度上非保守系统的Hamilton 原理。
由于

将式(9)代入式(6),得到

由式(10),利用分部积分计算,并考虑到端点条件(8)和互易关系(7),得到

由式(11),根据时间尺度上 Dubois-Reymond 引理,得到

将式(12)两边对 t 求 Δ-导数,有

方程(13)称为时间尺度上完整非保守力学系统的Lagrange 方程。
如果非保守力Qs≡0,则方程(13)成为时间尺度上Lagrange 方程
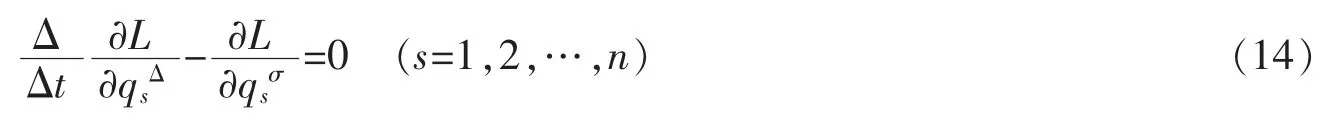
3 时间尺度上非保守系统的Noether对称性
引进时间尺度上时间t 和广义坐标qs的群的无限小变换

或其展开式

其中ε 是无限小参数,ξ0和ξs是无限小变换的生成元,表示非等时变分。
时间尺度上的Noether 对称性是指Hamilton 作用量(4)在群的无限小变换(15)下的不变性。 类似于文献[11],如果存在规范函数使得无限小变换的生成元 ξ0和 ξs满足广义 Noether 等式

其中
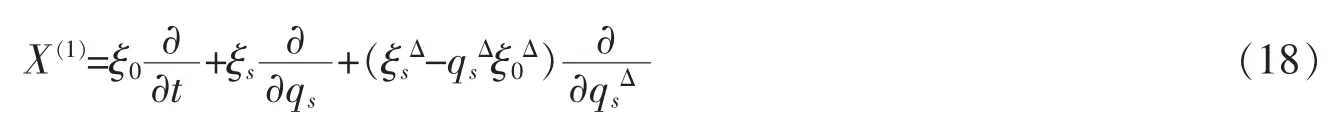
则相应不变性为时间尺度上完整非保守系统(13)的Noether 对称性。
4 时间尺度上完整非保守系统的Noether定理
由Noether 对称性可找到Noether 守恒量,对于时间尺度上完整非保守力学系统,有如下定理。
定理1对于时间尺度上完整非保守力学系统(13),如果无限小变换(15)的生成元ξ0和ξs满足广义Noether 等式(17),则

是该系统的Noether 对称性直接导致的Noether 守恒量。
证明将式(19)两边对 t 求 Δ-导数,并利用方程(13)和广义 Noether 等式(17),得到
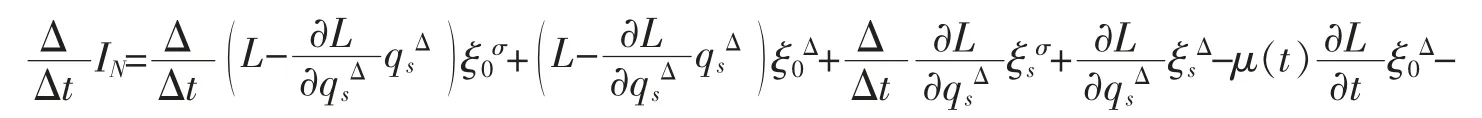
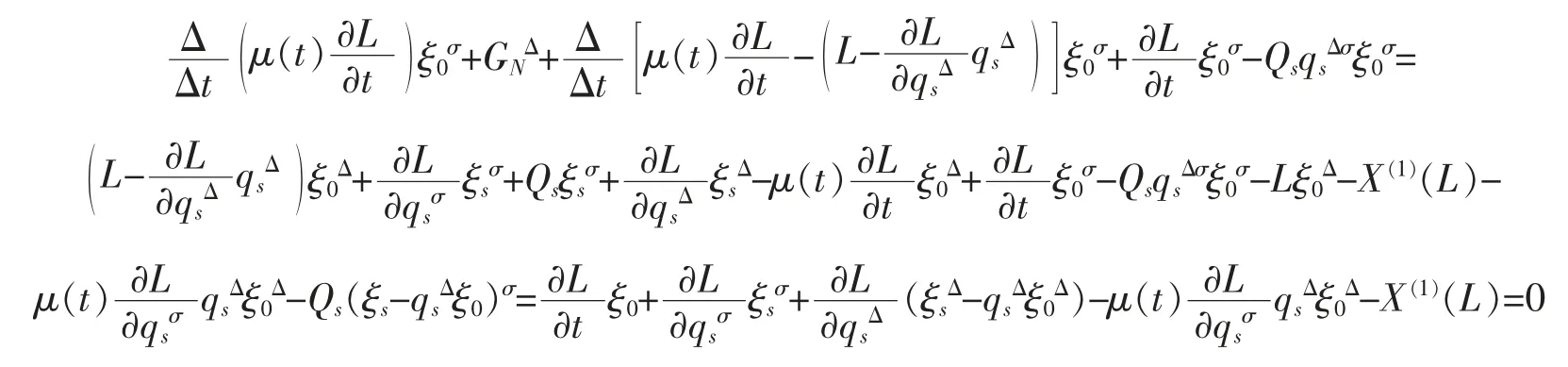
因此,沿着时间尺度上完整非保守力学系统的Lagrange 方程(13)的解曲线,式(19)是一个守恒量。 证毕。
定理1 可称为时间尺度上完整非保守力学系统(13)的Noether 定理。
如果非保守力Qs≡0,则定理1 给出时间尺度上Lagrange 系统的Noether 定理。 有如下定理。
定理 2对于时间尺度上 Lagrange 系统(14),如果无限小变换(15)的生成元 ξ0和 ξs满足如下的Noether 等式
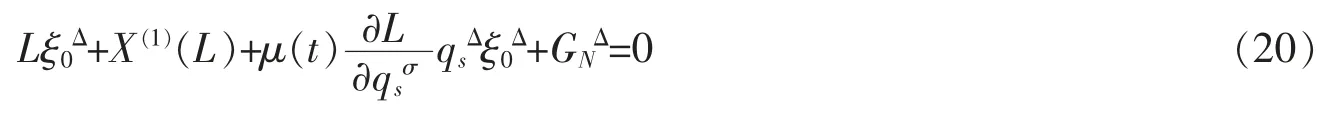
则系统存在Noether 守恒量,形如
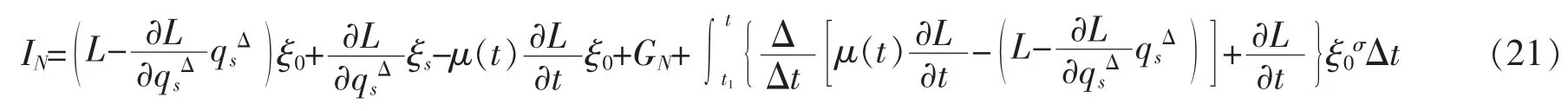
定理2 可称为时间尺度上Lagrange 系统(14)的Noether 定理。
如取时间尺度 T=R,则 σ(t)=t,μ(t)=0,此时方程(13)给出

这是经典情形下一般完整系统的Lagrange 方程。 容易验证成立如下关系式

因此,定理1 退化为
定理3对于完整非保守力学系统(22),如果无限小变换的生成元ξ0和ξs满足如下广义Noether 等式

则系统存在Noether 守恒量,形如

定理 3 是经典的一般完整系统(22)的 Noether 定理[18]。
5 算例
例1研究时间尺度上完整非保守力学系统,其Lagrange 函数为

非保守力为

设时间尺度为

试研究该时间尺度上完整非保守系统的Noether 对称性与守恒量。
由时间尺度(28),设 t=2m+1∈T,则向前跳跃算子为

因此,步差函数为

由式(26)和(27),根据方程(13),得到时间尺度上系统的动力学方程为

广义 Noether 等式(17)给出

方程(32)有解

生成元(33)和(34)都相应于系统的 Noether 对称性。 由定理 1,得

式(35)和(36)是与生成元(33)、(34)相应的 Noether 守恒量。
对于时间尺度上完整非保守系统,第二Euler-Lagrange 方程[7]可表为

将式(26)、(27)和(30)代入方程(37),显然方程(37)并不成立。 而如果取时间尺度 T=R,则容易验证方程(37)成立。
6 结语
时间尺度微积分为处理连续的、离散的或量子的以及混合的问题提供了一种统一的方法,为复杂系统动力学研究提供了一个重要的数学工具。 文章提出并研究了时间尺度上完整非保守力学系统的Noether 对称性与守恒量。 文章主要贡献在于:一是建立了时间尺度上非保守力学系统的Hamilton 原理,导出了时间尺度上完整非保守力学系统的Lagrange 方程。 二是给出了时间尺度上完整非保守力学系统的Noether 对称性的判据和广义Noether 等式。 三是建立了时间尺度上完整非保守力学系统的Noether 定理,并给出了定理的一个直接证明。 当不存在非保守力时,定理退化为时间尺度上Lagrange 系统的Noether 定理;当时间尺度取为实数集时,定理退化为经典完整非保守力学系统的Noether 定理。
