基于信道相关性的物理层安全性能分析

吴宣利，许智聪,2，王禹辰，李勇

（1.哈尔滨工业大学电子与信息工程学院，黑龙江 哈尔滨 150001；2.清华大学电子工程系，北京 100084；3.中国电子科技集团公司第五十四研究所，河北 石家庄 050081）

1 引言

在无线通信飞速发展的时代，通信系统的安全性能日益受到人们的重视。满足不同业务对于时延、能效、峰值速率、连接密度等指标的相关需求，将成为5G 移动通信发展的重要方向。但同时，系统安全性方面的问题亟待被研究，信息安全机制需要紧跟通信技术发展的步伐[1]。传统安全机制是建立在网络上层的密码加密体制以及安全协议体系，这种做法是以计算能力来换取信息的安全性，极大地增加了计算的复杂度。但是随着科技的进步，计算机的计算能力得到了指数级别的增长，这使复杂的密钥可能被强大的计算能力暴力破解。因此，在传统安全机制面临威胁的情况下，单一的密码体制亟待被完善，需要引入物理层安全新机制来增强系统的安全性。

物理层安全基于信息论的理论指导，利用物理层的自身特性实现保密通信，同时可以结合上层加密技术实现对系统的跨层安全设计，因此成为学者关注的热点问题。相较于有线通信系统，无线通信系统由于其部署不受地形条件的限制、作用范围更广泛的特点而具有一定的优势。然而，除了上述优势，无线通信系统由于无线信道具有开放性的特点，致使信息的安全传输存在隐患。近年来，随着对无线信道认知的完善，学者认识到无线信道随机衰落的特性为安全传输提供了有效保障，其核心在于利用信道的噪声和多径带来的随机性实现对传输信息的加密，提升主信道的通信质量，从而使非法窃听者获得的信息量趋于零。

物理层安全的本质是信息论安全，相关研究可以追溯到Shannon[2]提出的完全保密理论。在完美保密模型的基础上，Wyner[3]提出了窃听信道模型，证明了当窃听信道是主信道的某种退化形式时，存在某种安全编码，使发送端到合法接收端的信息安全传输速率最大化；同时定义该信息安全传输的最大速率为系统的保密容量。文献[4]研究了在主信道为无噪信道且窃听信道为其对称信道时，系统保密容量的解析表达式。文献[5]将保密容量的解析表达式推广至加性白高斯噪声（AWGN,additive white Gaussian noise）信道。然而，由于信息论安全模型过于理论化，文献[3]的研究最初并未受到研究者的广泛关注。随着无线通信的发展，人们对无线信道模型的研究更加充分。文献[6]研究了准静态瑞利衰落信道下的遍历保密容量及中断概率的解析表达式。针对上述基于保密容量的分析，学者通过人工噪声、功率分配等手段来提高系统的保密性能。文献[7]研究了主信道是AWGN 信道、窃听信道是瑞利衰落信道时，利用高斯随机码实现安全传输的方案。文献[8]研究了主窃信道均为瑞利衰落信道时的安全传输方案。文献[9]针对多天线目的节点提出一种切换分离式最优天线选择方案，给出相应的安全性能指标闭合表达式。文献[10]研究了私密信号和人工噪声之间的最优功率分配，并给出了人工噪声工作的临界信噪比。

上述研究均假设主窃信道相互独立，并不具有信道相关性。但是，受噪声、信道估计时差、窃听者位置等因素的影响，窃听者即使只是被动窃听，不对合法信息进行干扰，也能够从发送的信号中获得部分信道特征，这会影响系统的安全性能。此外，在实际的无线电环境中，合法接收者和窃听者之间的距离较近及其周围的散射体相似性较高，均会导致2 个接收机的接收信号之间存在高度相关性。在这些场景下，无法始终保证主信道的信道状态优于窃听信道，导致传输的信息不再安全[11]。文献[12]研究了瑞利衰落信道下，接收端处于高信噪比区域时系统遍历保密容量的表达式；文献[13]在此基础上研究了对数正态衰落信道下，接收端处于高信噪比区域时系统遍历保密容量的表达式。

通过上述分析可以发现，物理层安全利用无线信道的随机性，即使在主信道状态较差的情况下，仍然能够实现信息的安全传输。虽然现有文献分析了保密容量在相关衰落信道下，接收端处于高信噪比区域时的渐近性能，但是并未给出任意信噪比区域时系统遍历保密容量与中断概率的精确性能表达式。为了解决这一问题，本文首先建立了相关瑞利衰落信道的信道模型，通过合法接收端和窃听端的联合信噪比分布推导，得到了遍历保密容量和中断概率的精确性能表达式，并在此基础上得到了主窃信道的信道状态差异较大和较小2 种情况下，遍历保密容量和中断概率的渐近性能表达式。通过分析可以发现，当主窃信道相互独立时，较差的主信道状态会导致系统的保密容量趋于零；但主窃信道间相关性的存在使上述结论不再成立。因此，分析信道相关性对物理层安全性能的影响对保密系统的设计具有重要的理论意义和实际应用价值。本文的创新性总结如下。

1) 在相关瑞利衰落信道模型下，分析得到了接收端联合信噪比分布，在此基础上推导得到了遍历保密容量和中断概率的精确性能表达式。

2) 针对主窃信道状态差异较大和较小2 种不同的场景，分别得到了遍历保密容量和中断概率的渐近性能表达式。

3) 研究结果表明，相关性对系统安全性能的影响并不单一，而是与接收端的平均信噪比、信道增益比以及所设置的目标速率等多种因素有关。

2 系统模型

在实际的无线通信环境中，2 个信道之间的相关性是普遍存在的[14-15]。合法接收者和窃听者之间的距离较近及其周围的散射体相似性较高，均会导致2 个接收机的接收信号之间存在高度相关性，该相关性的产生与信道自身的特性有关，因此，本节首先分析产生相关性的因素，给出相关系数的计算式，并建立相关瑞利衰落信道系统模型。

2.1 相关系数

在多径衰落信道中，信道的相关性与时间差τ、多普勒频移fm、天线距离d、信号波长λ等信道特征参数有关。当合法接收端与窃听端之间的距离较近时，信道的时间相关性与空间相关性等价。信道相关系数可由式(1)计算[16]。

2.2 相关瑞利衰落信道模型

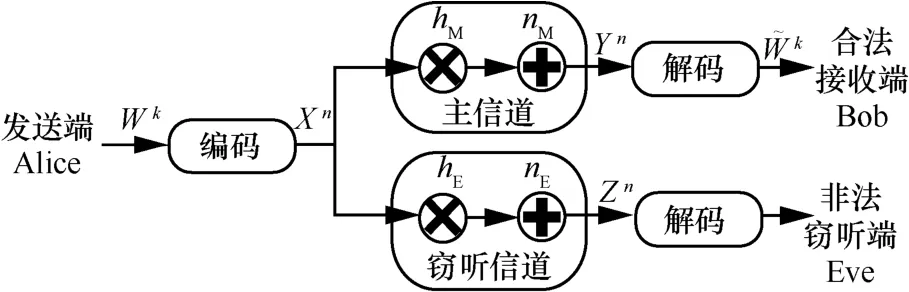
图1 考虑相关瑞利衰落信道的保密通信系统模型

由文献[17]可知，高斯随机变量可由相互独立的高斯随机变量的线性组合来表示，即hM、hE可分别表示为

其中，Cov[g]是协方差计算，E[g]是均值计算，D[g]是方差计算。由式(6)可知，变量X0和Y0的存在使信道衰落系数hM、hE之间具有相关性。同时，可以看出主窃信道之间的信道相关系数是在一段时间之内统计变量，而不是瞬时变量。

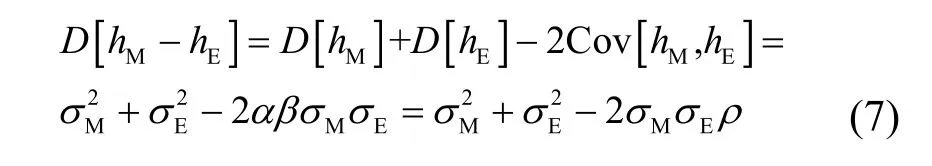
式(7)表明了相关系数对主窃信道的相似程度的影响。相关系数ρ越大，主窃信道差值的方差越小，表明二者的相似程度越高；反之，相似程度越低。

本文为简化分析，通过改变权重系数α和β使信道相关性变化，并对应无线信道中时间差τ、天线距离d等实际场景下信道参数的变化。结合式(1)和式(6)得到等价关系式为

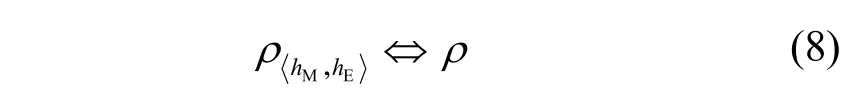
为求解接收端联合信噪比分布fγMγE(x,y)，根据图1 所示系统模型，接收端瞬时信噪比γM、γE可分别表示为

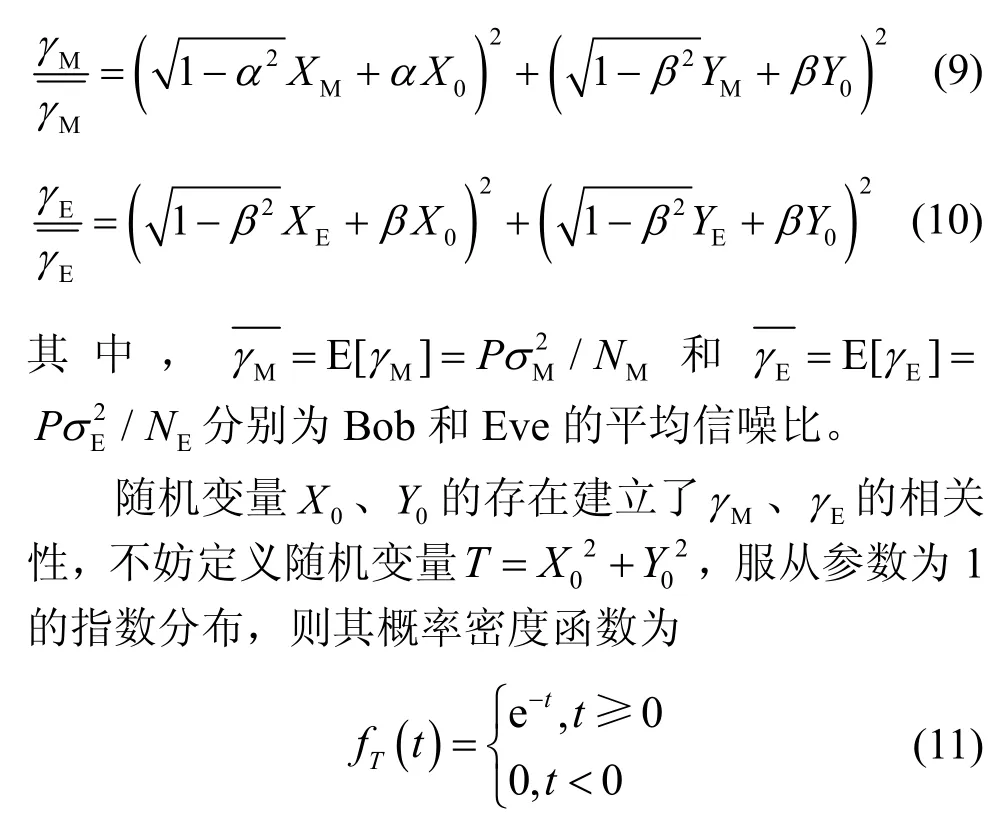
在条件T=t下，γM、γE服从非中心χ2分布[16]，则其条件概率密度分别为[18]

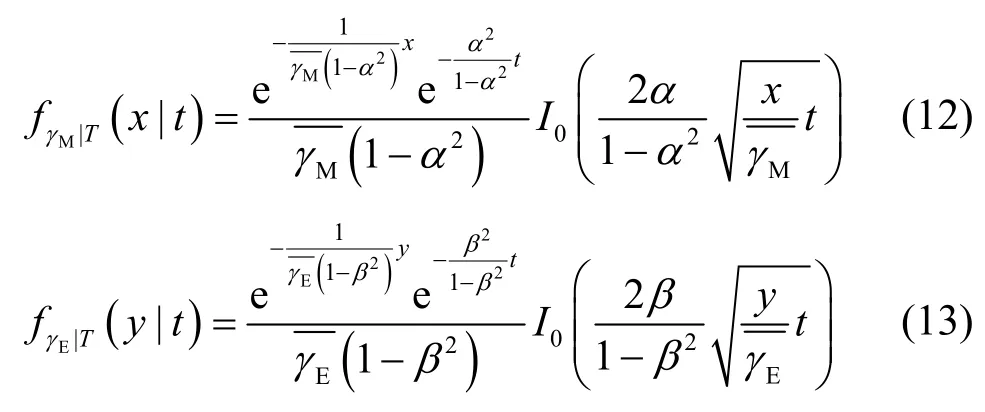
其中，I0(x)是第一类零阶修正贝塞尔函数。

结合式(11)～式(13)，可计算γM和γE的联合概率密度函数fγMγE(x,y)为

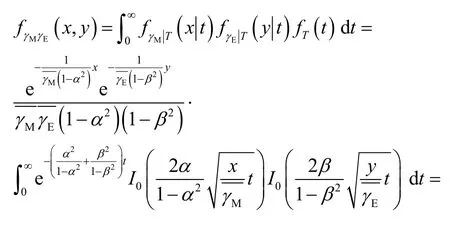
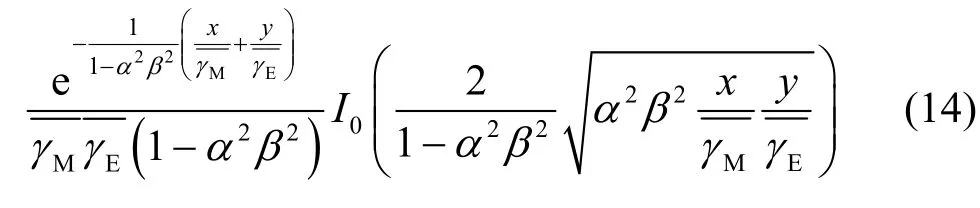
将式(6)代入式(14)可得

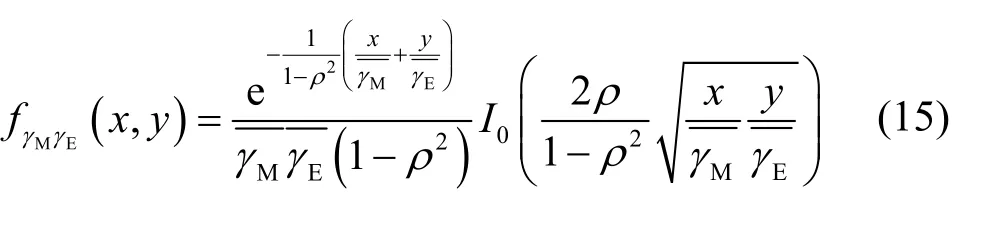
3 安全性能分析

本节将分析信道相关性对单输入单输出（SISO,single-input single-output）系统安全性能的影响，具体由遍历保密容量和中断概率2 个指标衡量。根据式(15)所示合法接收端和窃听端的联合概率密度函数，推导得到基于Marcum Q 函数表示的精确性能表达式，并在此基础上推导得到主窃信道的信道状态差异较大和较小2 种情况下的渐近性能表达式。

3.1 遍历保密容量分析

SISO 系统中，主信道和窃听信道的信道容量分别如式(16)和式(17)所示。

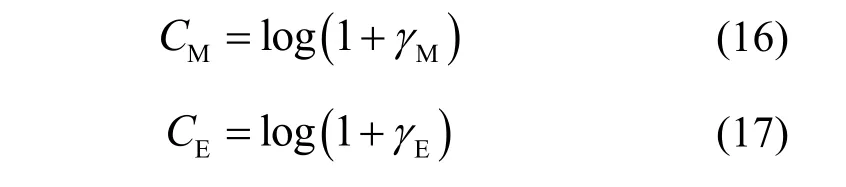
文献[6]给出了准静态瑞利衰落信道下SISO 系统瞬时保密容量的表达式，如式(18)所示。

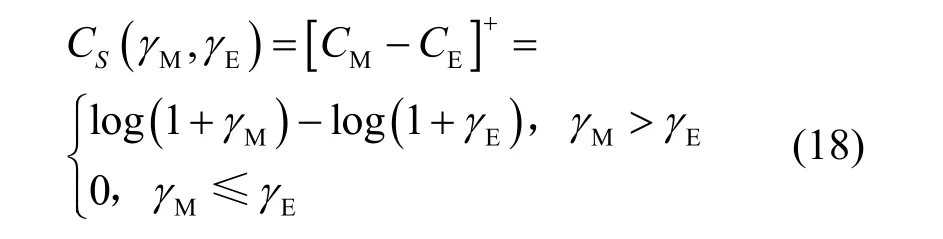
由于衰落信道具有随机性，因此瞬时保密容量同样表现出随机性。为消除随机引起的波动，通常采用遍历保密容量衡量衰落信道下系统的安全性能，其定义如下。

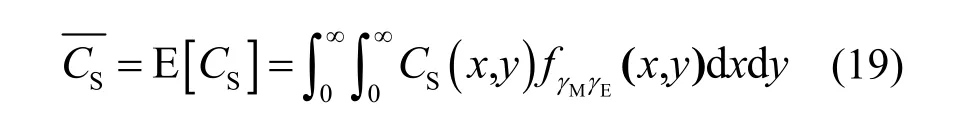
定理1主窃信道相关的场景下，遍历保密容量精确性能计算式为

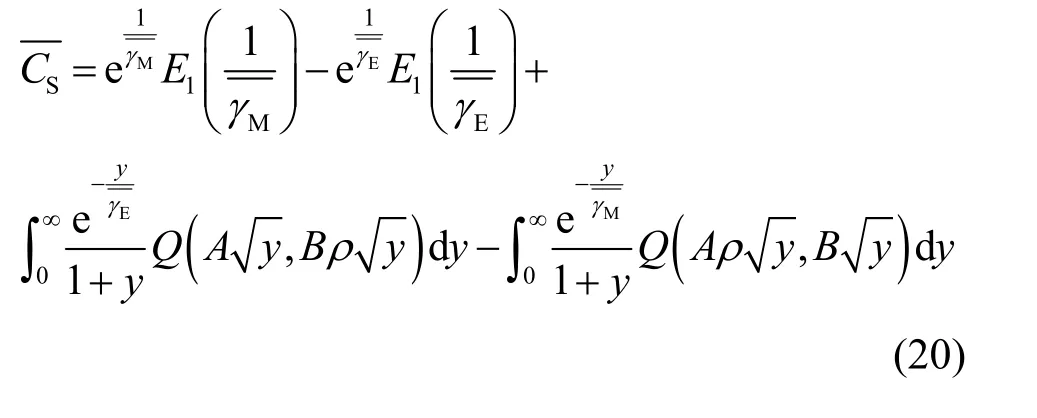
证明根据文献[19]可以得到式(19)的表达式为

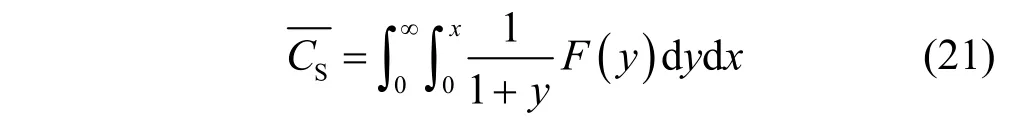
其中，F(y)为积分变限函数，定义为

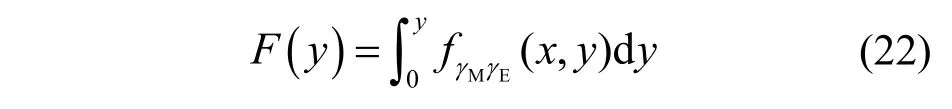
将式(15)代入式(22)可得

将式(23)代入式(19)可得

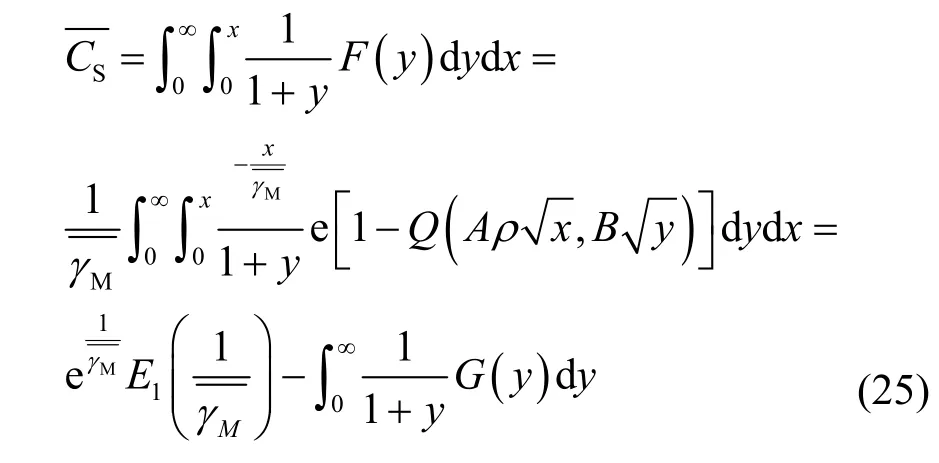
其中，E1(x) 为指数积分函数，定义为

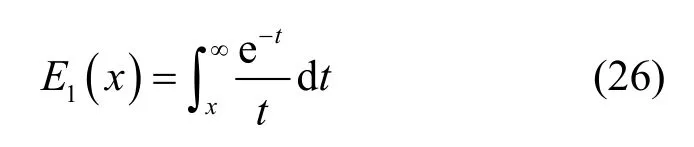
其中，G(y)同样为积分变限函数，定义为

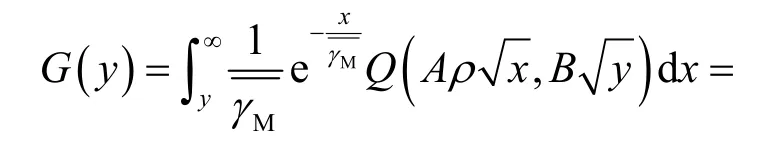
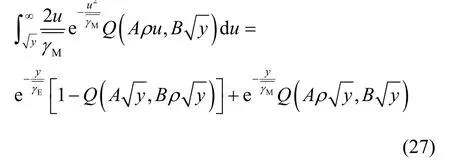
由文献[20]可得

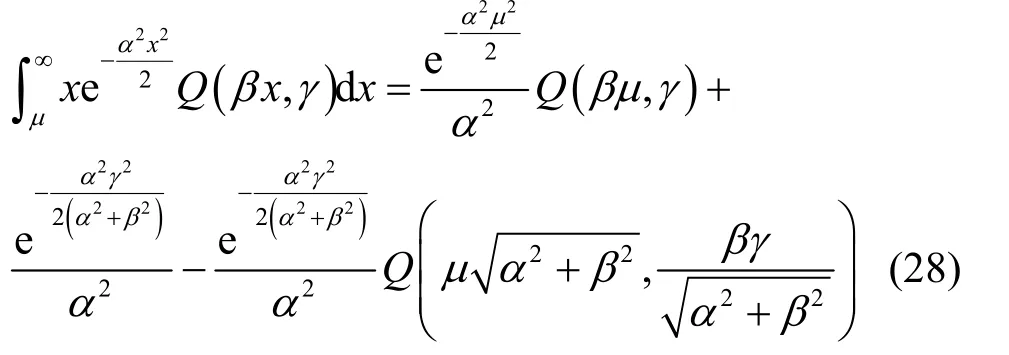
将式(27)代入式(25)，定理1 证毕。

证明根据Marcum Q 函数展开式(30)可得

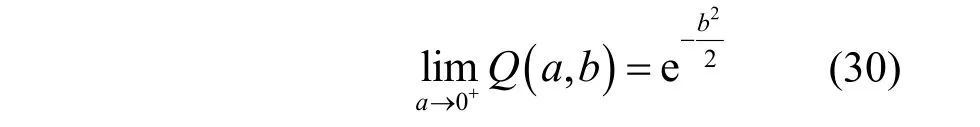
由于合法接收端通常处于高信噪比区域，即→∞，对应于系数A→ 0+。将式(30)代入式(20)，可得近似值为

根据式(32)，可近似认为

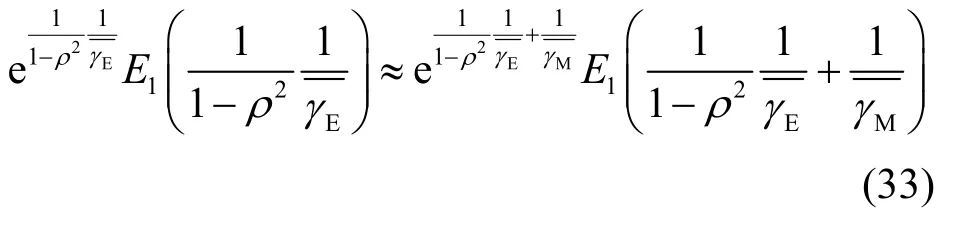
将式(33)代入式(31)，推论1 证毕。

由于主窃信道的遍历信道容量分别为

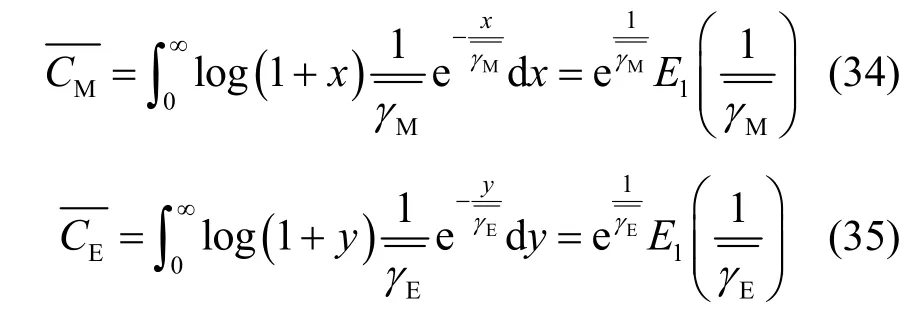
结合式(34)、式(35)和式(29)可得

由式(36)可知，在该场景下，遍历保密容量与信道的相关性无关，只与主窃信道的信道增益有关，且增强信号强度有利于提高安全通信的速率。

3.2 中断概率分析

中断概率是用于可靠和安全传输系统的有效设计的重要指标，实际上，文献[21]的研究已表明，通过允许一定的中断可能性，可以大大提高通信速率。文献[22]给出了中断概率的定义，即系统的安全传输速率CS小于目标速率RS时的概率，中断概率定义式为

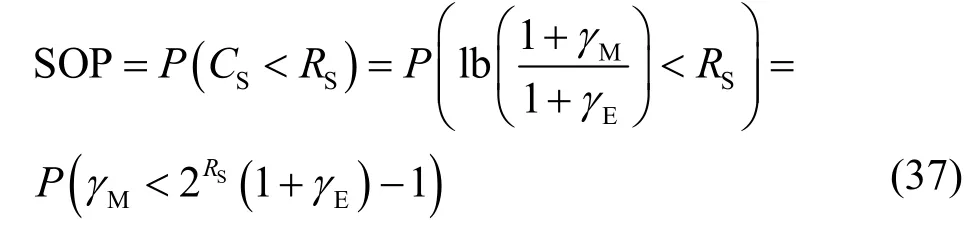
由二维联合概率分布，式(37)可重写为

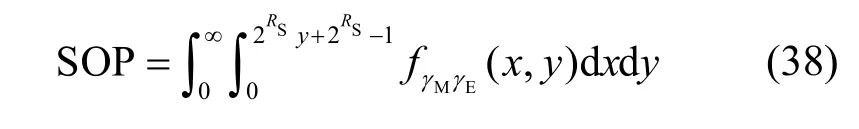
定理2主窃信道相关的场景下，中断概率的精确性能计算式为

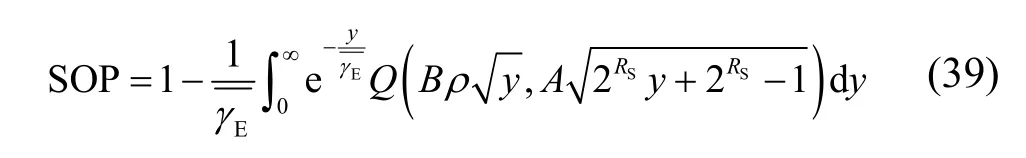
证明根据式(37)，可定义积分变限函数T(x)，由式(14)可知，变量x、y的地位对等，因而函数T(x) 和F(y)应具有相同的形式，即

将式(40)代入式(38)可得

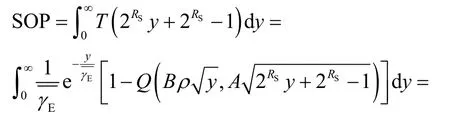
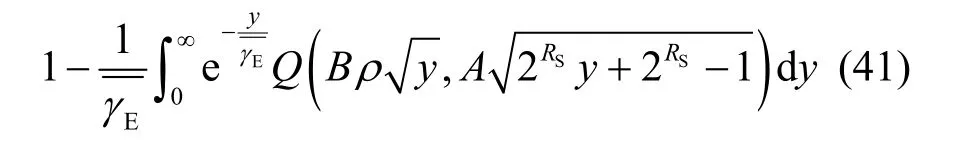
综上，定理2 证毕。

推论2在实际场景中，对应于主窃信道状态差异较大的场景，即合法接收端通常处于高信噪比区域（→∞），窃听端平均信噪比有限，系统中断概率的渐近性能计算式为

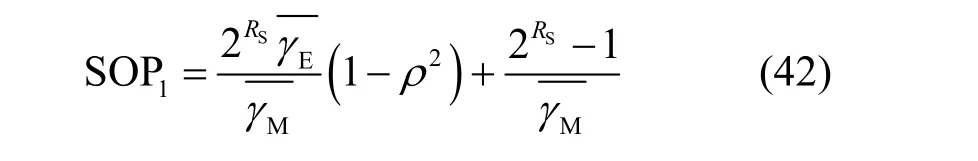
证明根据Marcum Q 函数展开式可得

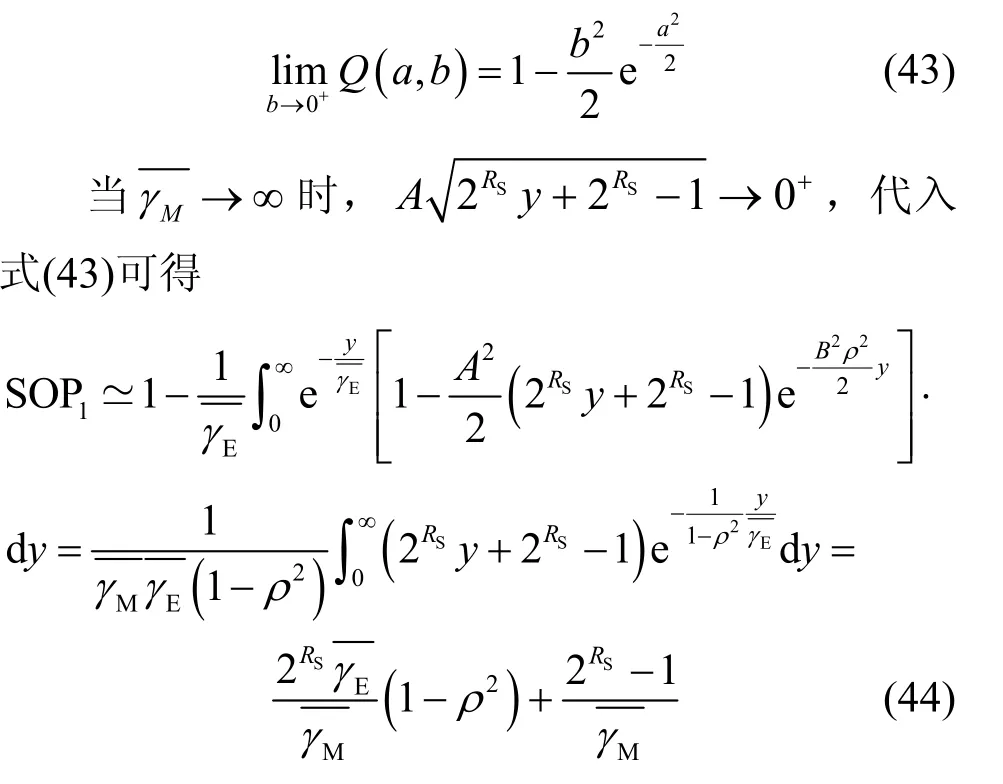
综上，推论2 证毕。

由式(42)可知，主信道信号强度的增大会降低系统的中断概率，且相关性的增强也会导致中断概率减小，这表明在接收端处于高信噪比区域时，相关性有利于系统安全。

当信道状态固定时，需要合理控制目标速率RS来满足系统中断概率的需求。若给定中断概率δ，使通信中断的概率不超过δ，如式(45)所示。

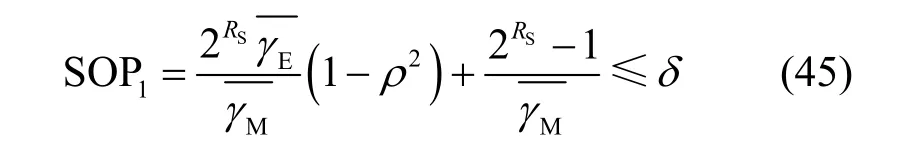
则可以得到目标速率RS的设置范围为

证明当合法接收端平均信噪比→∞，且信道增益比K有限时，中断概率定义式等价于

定义一个新随机变量U=γM/γE，则中断概率由其累积分布函数计算

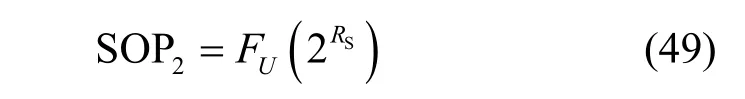
文献[12]中给出了FU(u)的表达式为

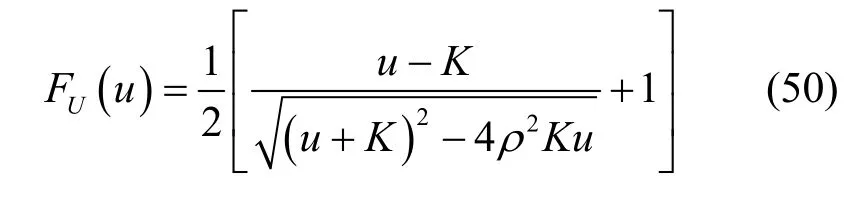
结合式(49)和式(50)，推论3 证毕。

由式(50)可知，在该场景下，中断概率不再随合法接收端平均信噪比的增大而降低，而只与信道相关性、信道增益比有关。因此，当信道增益比有限时，只能通过改变信道相关性、信道状态差异或目标速率来降低通信中断的概率。

由上述分析可知，为了降低中断概率，必须满足0＜RS＜lbK。给定中断概率δ，使通信中断的概率不超过δ，如式(51)所示。

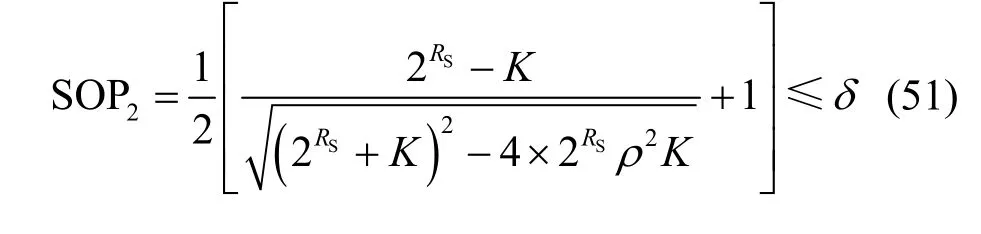
则可以得到目标速率RS的设置范围为

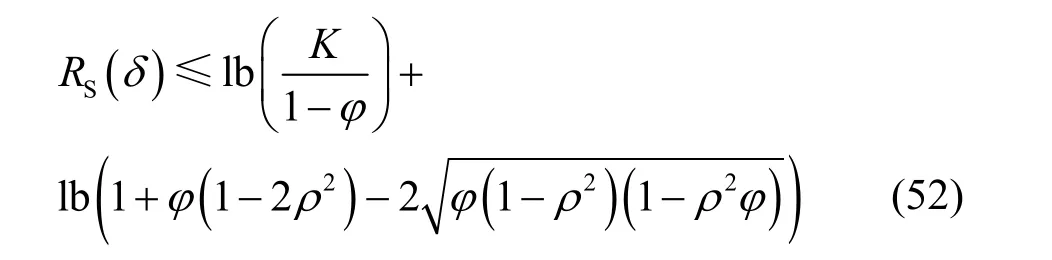
其中，φ=(2δ-1)2。

4 仿真分析

本节通过蒙特卡罗仿真验证理论分析的正确性，假设主窃信道均为准静态瑞利平坦衰落信道。

4.1 主窃信道状态差异较大场景

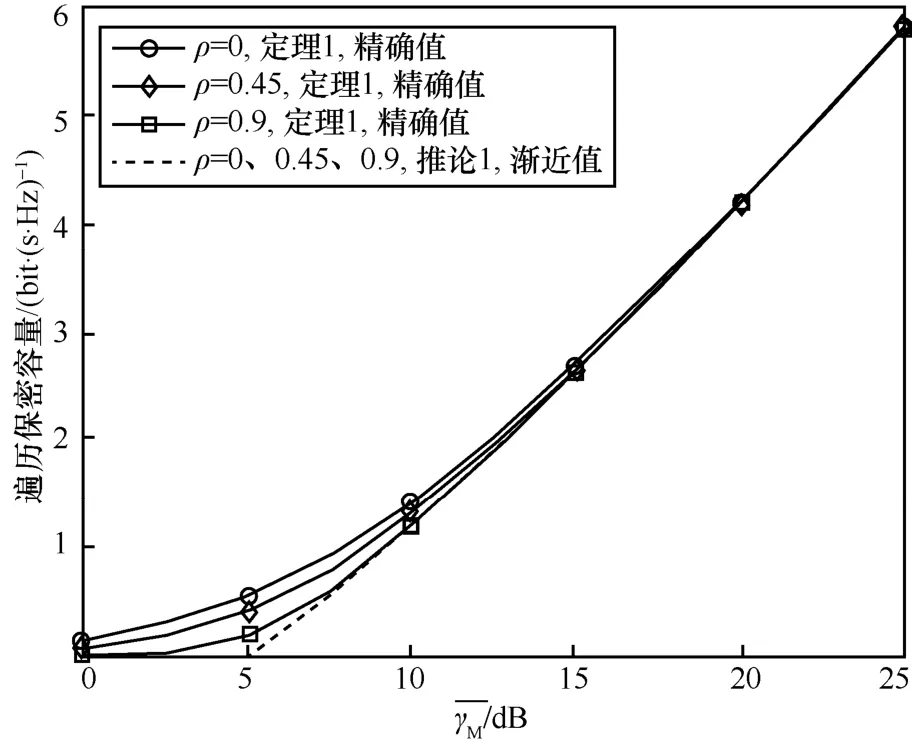
图2 遍历保密容量与平均信噪比的关系

仿真验证了式(20)和式(35)理论分析的正确性，由图2 可得如下结论。

1) 遍历保密容量随合法接收端平均信噪比的增大而增大。这是由于当主信道的信道状态远好于窃听信道时，主信道的信道容量占主导地位，根据式(34)，当平均信噪比增大时，主信道的信道容量增大，因而系统安全传输速率增大。

3) 在[K]∈[0,10]dB 的区间内，相关性对遍历保密容量造成的影响较大，这说明当信道增益差异较小时相关性对系统安全的影响最大。当→0时，主信道增益较差，因而保密容量趋于零。当[K]＞10 dB时，主信道状态较好，窃听端产生的影响较小，进而使相关性不产生影响。此外，当[K]∈[0,10]dB 时，该场景下窃听端不可忽略，相关性是影响容量的主要因素；且强相关性意味着主窃信道的信道估计具有高度相似性，由于瞬时保密容量为主窃信道的信道容量之差，因此强相关会使瞬时保密容量减小，进而造成遍历保密容量损失。

主窃信道状态差异较大的场景下中断概率SOP与平均信噪比的关系如图3 所示。仿真参数设置如下：合法接收端平均信噪比设置为[0,30]dB；窃听端平均信噪比=5 dB；相关系数ρ设置为[0,0.45,0.9]；目标速率RS设置为0.3bit/(s.Hz)。

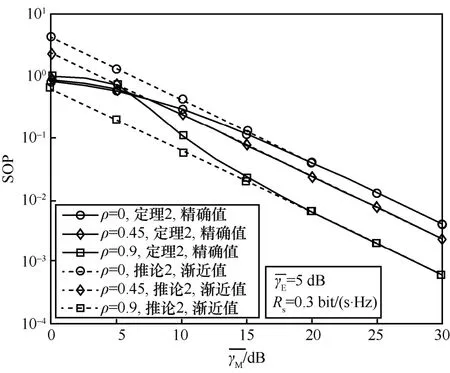
图3 中断概率与平均信噪比的关系

仿真验证了式(39)和式(42)所示的理论分析的正确性，由图3 可得如下结论。

1) 中断概率随合法接收端平均信噪比的增大而减小，且随着，中断概率减小的速度变快，说明增大主窃信道的信道增益差异有利于显著提升系统的安全性能。

2) 由图3 可知，中断概率的精确分析曲线与相关系数的关系分为2 种趋势。在高信噪比区域，中断概率随相关系数的增大而减小，表明在高信噪比区域，相关性有利于系统安全，能降低通信中断的概率；在低信噪比区域，中断概率随相关系数的增大而不断增大，表明在低信噪比区域，相关性不利于系统安全，会增加通信中断的概率。这是由于相关性的强弱会影响主窃信道增益的方差（如式(7)所示），进而影响系统遍历保密容量的方差。具体而言，强相关性对应瞬时保密容量的方差减小，这意味着瞬时容量小于目标速率的次数减少，表现为中断概率降低。

4.2 主窃信道状态差异较小场景

文献[11]研究了主窃信道状态差异较小的场景下遍历保密容量与平均信噪比的关系，因此本节只针对该场景下的中断概率进行仿真验证。

中断概率下界值SOP2与相关系数ρ的关系如图4 所示。仿真参数设置如下：信道增益比K=5；相关系数ρ设置为[0,0.9]；目标速率RS设置为[0.1,0.3,2.5,3]bit/(s.Hz)。

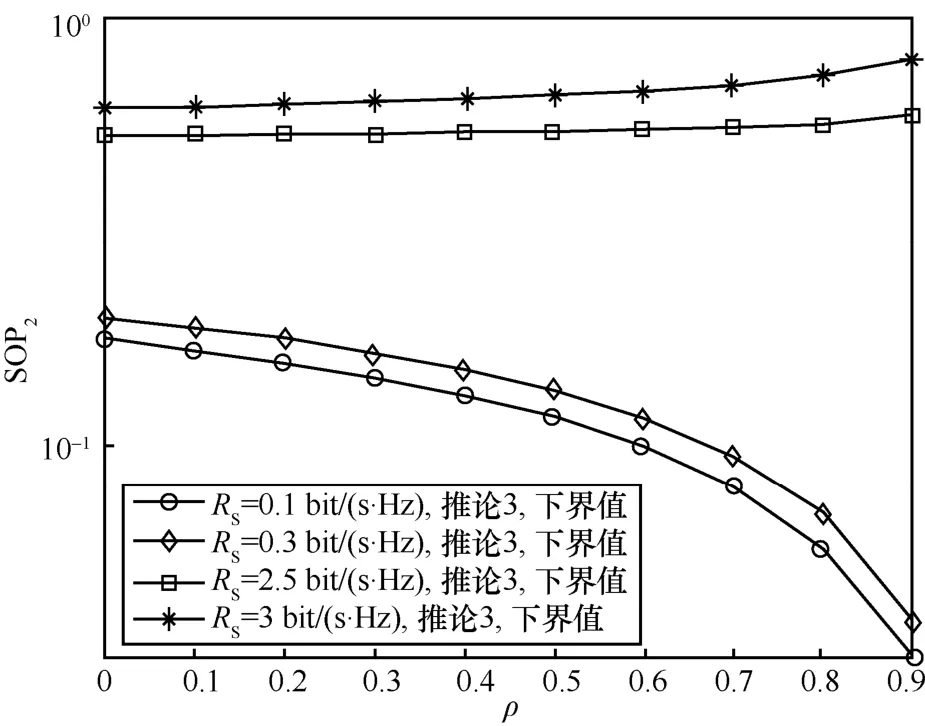
图4 中断概率下界与相关系数的关系

仿真验证了式(47)理论分析的正确性，由图4可得如下结论。

1) 当2RS＜K时，相关性对中断概率的影响较大，且中断概率随相关系数ρ的增大而减小，最终趋于零，这说明相关性有利于系统安全。在强相关区域内，系统中断概率变化较大，随相关性增强而显著减小。

2) 当2RS＞K时，相关性对中断概率的影响较小，且随相关系数ρ的增大，中断概率逐渐增大，最终趋于1，这是由于相关性的强弱会影响主窃信道增益的方差（如式(7)所示），进而影响系统遍历保密容量的方差。具体而言，强相关性对应于瞬时保密容量的方差减小，当目标速率越大时，瞬时容量小于目标速率的次数增大，表现为中断概率的增加，且随ρ→1 而SOP →1，这说明此时相关性不利于系统安全。

由上述分析可知，目标速率RS和信道增益比K之间存在着相互制约的关系。这是由于信道增益比决定了系统安全通信的速率，如果目标速率设置得较大，显然会增大通信中断的概率。因此在得到信道增益比的情况下，可以通过合理设置目标速率达到维护系统安全的目的，通常为保证中断概率满足要求，往往需要调整目标速率使其满足RS＜lbK的关系，更进一步地，式(52)给出了精确目标速率的取值范围。

在上述仿真的基础上，分析了强相关区域内（ρ≥0.7）中断概率SOP 与平均信噪比的关系，如图5 所示。仿真参数设置如下：信道增益比K=5，合法接收端平均信噪比设置为[0,30]dB，相关系数ρ设置为[0.7,0.8,0.9]，目标速率RS设置为0.3 bit/(s.Hz)。

图5 中断概率与平均信噪比的关系

由图5 可得如下结论。

1) 中断概率随合法接收端平均信噪比的增大而逐渐减小，但在→∞时达到下界，式(47)和图5描述了该下界与相关系数ρ的关系，这表明只有通过改变信道增益比或信道相关性才能改善系统的安全性能。

2) 在任意信噪比条件下，中断概率随相关系数的增大而减小，表明相关性有利于系统安全。这是因为，目标速率RS设置的值较小，会导致瞬时保密容量的均值大于目标速率，由于强相关性对应于瞬时保密容量方差的减小，即瞬时容量小于目标速率的次数减少，进而表现为中断概率的降低。

5 结束语

本文对相关瑞利衰落信道下的物理层安全性能进行了研究。首先，分析了无线信道参数对信道相关性的影响；然后，研究了信道相关性对遍历保密容量和中断概率的影响。研究结果表明，当主窃信道增益差异较大时，在高信噪比区域内，相关性不影响系统的遍历保密容量，但会降低系统的中断概率；在低信噪比区域内，相关性会造成遍历保密容量的损失，且会增大系统的中断概率，不利于系统安全。当主窃信道增益差异较小时，在任意信噪比区域内，相关性会造成遍历保密容量的损失和系统中断概率的降低。基于上述结论，可以根据当前接收端获得的信噪比、信道增益比、信道相关性等条件进行安全编码等方式，来维护系统安全性能。