CaputoΔ型分数阶时间尺度Noether 定理1)
2021-11-09田雪张毅
田 雪 张 毅
* (南京理工大学理学院,南京 210094)
† (苏州科技大学土木工程学院,江苏苏州 215011)
引言
分数阶微积分几乎和整数阶微积分同时存在,它的导数和积分的阶数可以是任意数[1].由于分数阶微分方程具有独特的能力来描述自然现象的共同特征−异常行为和记忆效应[2],因此分数阶微分方程能比整数阶微分方程更准确地描述许多实际问题.分数阶微分方程理论是数学的一个重要分支,包括连续分数阶微分方程和离散分数阶差分方程.在过去的数十年里,分数阶微分方程理论得到了广泛的普及和应用[3-8],但这些连续分数阶微分方程和离散分数阶差分方程是被分开研究的.1988 年Hilger[9]发现了离散系统和连续系统之间有许多相似之处,因此提出了一个关于微分方程和差分方程的统一理论−时间尺度.随后,Bohner 等[10-12]意识到时间尺度微积分弥合了连续和离散系统之间的差距,这个统一的方法意味着在复杂的新模型中可以考虑更多的变量.不仅如此,当时间尺度为T=qN0(q>1,N为自然整数集)或T=qZ∪{0} 时,时间尺度上的微分方程可以表示成在量子理论中有着重要应用的q差分方程[11].因此,利用不同的时间尺度T,分数阶时间尺度微积分可以同时处理连续、离散和量子分数阶微积分.例如,取T=R (R 为实数集)时,分数阶时间尺度微分方程则成为[1]中经典的分数阶微分方程;当T=Z (Z 为整数集)时,其分数阶时间尺度微分方程与文献[6]中步长为1 的离散分数阶差分方程是一致的;若T=qN0(q>1),其微分方程则成为文献[7]中的离散分数阶q差分方程.近年来,分数阶时间尺度微积分已被应用于动力学方程[13]、最优控制[14]等领域.虽然力学系统的分数阶Noether 定理和时间尺度Noether 定理被广泛研究与应用,但分数阶时间尺度Noether 定理是一个新的研究课题[15].
众所周知,Noether 定理揭示了对称性和守恒量之间的内在关系[16].在群的无限小变换下作用量的不变性(Noether 对称性)意味着沿着系统的动力学真实运动轨道上存在一个守恒量(Noether 守恒量).相比牛顿力学和Lagrange 力学,运用Noether 对称性可以找到除了能量守恒、动量守恒或动量矩守恒之外更多的且相互独立的守恒量[17].因此,近些年人们致力于研究力学系统的Noether 定理[18-25].而利用时间尺度理论得到的Noether 定理,通过选择不同的尺度可同时表示连续时间变量、离散时间变量甚至分段时间变量的Noether 定理.
2004 年Bohner[26]研究了Δ导数的时间尺度变分问题,建立了时间尺度Lagrange 方程.此后,有关时间尺度变分原理和时间尺度Lagrange 方程的理论不断得到完善[27-30],为研究时间尺度Noether 定理奠定了基础.2008 年Bartosiewicz 和Torres[31]分别在特殊无限小变换和一般无限小变换的情况下研究了时间尺度的Noether 定理.随后,Bartosiewicz 等[32]给出了Δ导数的时间尺度第二类Lagrange 方程,并利用该方程证明了文献[31]中的Noether 定理.之后,各种力学系统的时间尺度Noether 定理被建立,如最优控制问题[33]、非保守系统[34-36]、非完整系统[37-38]、Hamilton 系统[39-40]、Birkhoff 系统[40-42]、时滞系统[43-44]等.然而,最近Anerot 等[45]指出文献[32]中所推导的时间尺度第二类Lagrange 方程是错误的.因此,在上述列举的文章中,利用该方程得到的力学系统的Noether 定理其正确性有待商榷.Anerot 等[45]利用一种广义Jost 方法来研究 ∇ 导数时间尺度迁移和非迁移系统的Noether 定理,并且用了一些算例来证明他们的结果.同样,Cresson 等[46]将Jost 方法推广到分数阶理论,建立了分数阶Noether 定理,并给出了一些应用和仿真.本工作利用分数阶时间尺度Hamilton 原理,推导了CaputoΔ型分数阶时间尺度Lagrange 方程,在一般无限小变换下利用广义Jost 方法建立了CaputoΔ型的分数阶时间尺度Noether 定理.文末对分数阶时间尺度Kepler 问题和线性振动系统进行模拟,说明了定理的正确性.
1 预备知识
设T是一时间尺度,t∈T,定义前跳算子σ:T→T为 σ(t)=inf{s∈T:s>t},后跳算子ρ:T→T为ρ(t)=sup{s∈T:s
定义1设T是一时间尺度且Tκ=T,定义右连续函数hα:T×T→R,α≥0 为[48]
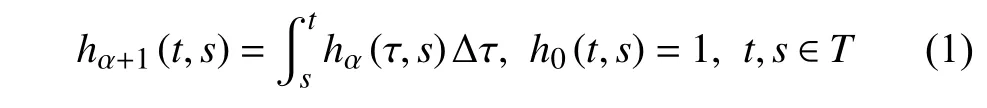
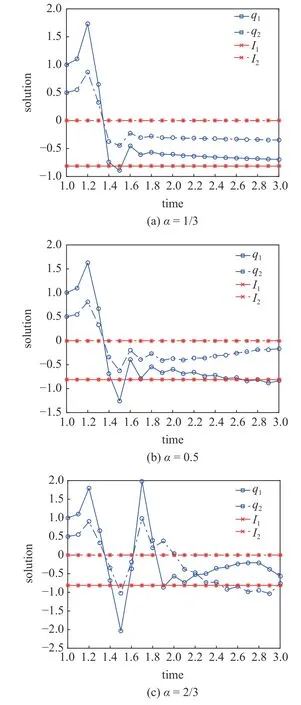
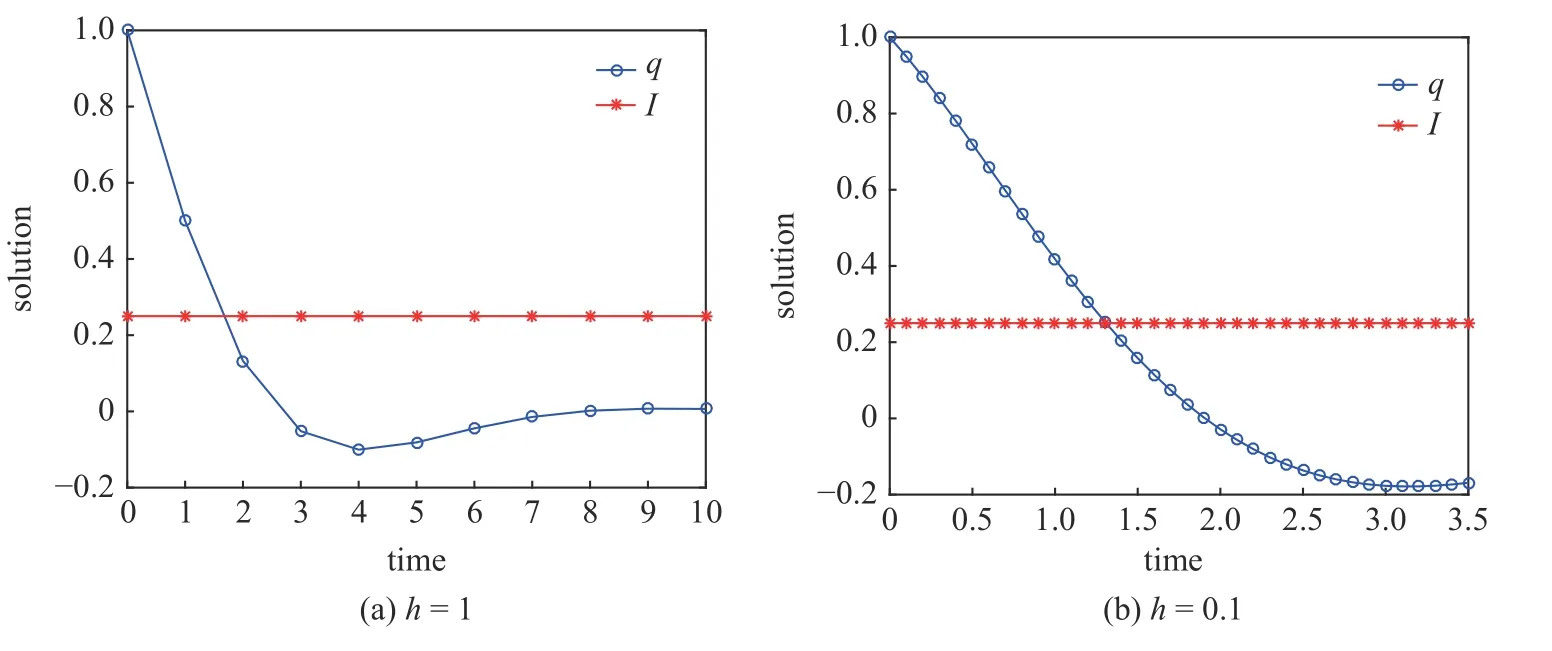
定义2设T是一时间尺度,函数f:[a,b]⊂R,其中,α≥0,a,b∈R,a 右Riemann-Liouville 分数阶Δ积分为 注1:若T=R,有,则 式(4)和式(5)是传统的左、右Riemann-Liouville分数阶积分[1]. 注2:若T=Z,可定义 式(7)和式(8)是离散的左、右Riemann-Liouville分数阶积分. 注3:若T=pN0,p>1,令α∈[0,∞)N0,a,t∈T,t≥a,p分数阶函数可定义为 式(10)和式(11)可分别称为p离散的左、右Riemann-Liouville 分数阶积分. 定义3设T是一时间尺度,函数f:T→R,定义,n∈N0,定义左Riemann-Liouville分数阶Δ导数为[47] 右Riemann-Liouville 分数阶Δ导数为 注4:若 α<0,可定义 注5:假设 α≥0,m=+1.若m=0,则有 若m=1,则有 定义4设T是一时间尺度,t∈T,α≥0,定义左Caputo 分数阶Δ导数为[47] 右Caputo 分数阶Δ导数为 注6:若 α∈(0,1),即m=1,则有 当f(a)=0时,左Caputo 分数阶Δ导数与左Riemann-Liouville 分数阶Δ导数一致;当f(b)=0 时,右Caputo 分数阶Δ导数就与右Riemann-Liouville分数阶Δ导数一致. 同样地,当T=R,式(18)和式(19)则成为传统的左、右Caputo 分数阶导数;当T=Z,式(18)和式(19)成为离散的左、右Caputo 分数阶导数;当T=pN0,p>1,式(18) 和式(19) 则成为p离散的左、右Caputo 分数阶导数. 引理1设函数f,g:T→R在点t∈Tk是Δ可微的,a,b∈T,则有[10] 若 ω=ν−1:T¯ →T,则有 其中 νΔ≠0.若f:T→R是右连续的,并且 ν 的右连续导数可微,则有其中a,b∈T. 引理4假设函数f,g:T→R,a,b∈T,分数阶时间尺度分部积分公式如下[49] 假设力学系统的位形是由n个广义坐标qk(k=1,2,···,n)确定的.设分数阶时间尺度系统的作用量为 CaputoΔ型分数阶时间尺度Hamilton 原理为 其满足交换关系 和边界条件 对式(28)进行变分运算,得 根据分数阶时间尺度分部积分公式(26),再由式(30)和式(32),可得 将式(33)代入式(32),则有 由式(22)和式(31),方程(34)可写为 根据引理2,可得 在式(36)两边对t求Δ导数,有 方程(37)则是CaputoΔ型分数阶时间尺度运动微分方程,将它称为分数阶时间尺度Lagrange 方程. 注7:若 α=1,方程(37) 则成为时间尺度Lagrange 方程[31] 注8:若T=R,方程(37)则成为Caputo 型分数阶Lagrange 方程 注9:若 α=1,T=R,方程(37) 则成为经典的Lagrange 方程 引进单参数群的特殊无限小变换 式中 ξk(k=1,2,···,n) 是无限小生成元,ε 是无限小参数. 定义5对任意的 [ta,tb]⊆[a,b],ta,tb∈T,若有 则称Hamilton 作用量式(28)在特殊无限小变换式(41)下是不变的. 判据1若Hamilton 作用量式(28)在特殊无限小变换式(41)下是不变的,则有 证明:由定义5 可知,对任意的子空间[ta,tb]⊆[a,b],条件式(42)都成立,所以有 在式(44)中对 ε 求导,再令 ε=0,利用分数阶时间尺度Caputo 导数的定义和性质,可得 则记 定理1若Hamilton 作用量(28)在定义5 的意义上是不变的,则存在守恒量 证明:对式(48)中的I求Δ导数,则有 由分数阶时间尺度Lagrange 方程(37)可知 将式(50)代入式(43),可得 即IΔ=0,因此可证明式(48)是特殊无限小变换下的Noether 守恒量. 注10:若 α=1,定理1 成为特殊无限小变换下的时间尺度Noether 定理[31] 本节研究一般无限小变换下的分数阶时间尺度Noether 定理.首先,引进单参数 (Δ,T) 可容许投射群[45]的一般无限小变换 式中 ζ,ξk(k=1,2,···,n) 是无限小生成元,ε 是无限小参数. 定义6对任意的 [ta,tb]⊆[a,b],ta,tb∈T,若有 则称Hamilton 作用量式(28)在一般无限小变换式(53)下是不变的. 判据2若Hamilton 作用量式(28)在一般无限小变换式(53)下是不变的,则有 证明:由定义4 和引理3,可得 由定义6 可知 由于 [ta,tb]是 [a,b] 的任意子空间,则方程(57) 等价于 在式(58)中对 ε 求导,再令 ε=0,得 注11:考虑到 不变性的条件(57)可写为 接下来,引进扩展Lagrange 函数L:R×[a,b]×Rn×R∗×Rn→R被定义为 其作用量用SL表示,被定义为 设时间尺度束类路径[45]被定义为 当tΔ=1,则有 在 F 上的不变性条件(57)可写成 在方程(66)中对 ε 求导,再令 ε=0,则有 在 F 上可简化成如下的方程组 将式(69)代入式(67),得 因此,可得到如下的CaputoΔ型分数阶时间尺度Noether 定理. 定理2若Hamilton 作用量(28)在定义6 的意义上是不变的,则存在守恒量 注12:若 α=1,式(73)成为 注13:若T=R,式(73)成为 例1众所周知,Kepler 问题是牛顿力学中最早解决的问题之一,Kepler 系统也是最早发现的可积系统之一.Kepler 问题仍在研究中,并被广泛应用于各个领域.Eleonskiĭ等[50]指出分数阶Kepler 问题中所有有限运动的轨道也是封闭的.Anerot 等[45]研究了平面上的时间尺度Kepler 问题的Noether 定理.在这里,我们考虑定义在上的CaputoΔ型分数阶时间尺度Lagrange 函数 其表示Kepler 问题中两个质量为1 的相互作用粒子的Lagrange 函数.其中,用分数阶导数代替了存在能量耗散的运动的速度.当T=R且α=1时,分数阶时间尺度Lagrange 函数式(79)就是传统的Kepler 问题.根据分数阶时间尺度Lagrange 方程(37),可得 考虑到判据2,可得 这样,我们可以得到两组无限小变换的解 由定理2,可以得到两个守恒量 如果初始条件满足q1(1)=1,q2(1)=0.5,v1(1)=1和v2(1)=0.5,考虑在时间尺度为T=λZ 上研究运动轨迹q1,q2和守恒量I1,I2.此时hα(t,s) 则为 令a=0,则t≥1.首先,当 α=0.5时,分别在 λ=0.1,λ=0.5,λ=1和λ=2的情况下模拟q1,q2,I1,I2的值,得到的结果如图1 所示. 从图1 可以看出,在不同的时间尺度上,轨迹q1和q2各不同,I1的值也不同,但是I2≡0.这表明在这些初始条件下I2是一个平凡守恒量.但在不同的时间尺度上,I1和I2始终是常数,从而验证了定理2 的正确性.I1和I2不仅在不同的时间尺度上是常数,并且在分数阶导数 α 取不同值的情况下也是常数.令λ=0.1,当 α=1/3,α=0.5,α=2/3时q1,q2,I1,I2在时间段 [1,3] 上的值如图2 所示. 图1 α=0.5 时 q1,q2 ,I1 ,I2 的值Fig.1 Simulation of q1,q2 ,I1 ,I2withα=0.5 从图2 可以看出,当在同一时间尺度上而 α 不同时,I1和I2不仅是常数且其值也没发生变化.若α=1,则Kepler 问题的时间尺度Lagrange 方程为 图2 λ=0.1 时 q1,q2 ,I1 ,I2在 [1,3] 上的值Fig.2 Simulation of q1,q2 ,I1 ,I2on [1,3]withλ=0.1 从而守恒量为 图3 证明了当 α=1时,CaputoΔ型分数阶时间尺度Noether 定理可以简化为文献[45]中的时间尺度的Noether 定理. 图3 α=1 时 q1,q2 ,I1 ,I2在 [0,10] 的值Fig.3 Simulation of q1,q2 ,I1 ,I2on [0,10]withα=1 例2由于分数阶导数和积分具有记忆效应,分数阶微积分为描述阻尼材料和黏弹性材料提供了更切实的模型.以单自由度线性分数阶振动系统为例,其Lagrange 函数为 在时间尺度T={tk=a+kh,k∈N} 上求其Noether 守恒量. 由分数阶时间尺度Lagrange 方程(37),得 若T=R,α=1,方程(91)则成为经典的阻尼振子 则可称方程(91)为分数阶时间尺度阻尼振子.由判据2,有 方程(93)有解 由定理2,得到守恒量 令a=0,γ=1,α=0.5,h=1,初始位置为q0=1,初始速度为v0=−0.5.当t=t0时,I0=−0.125,并且 由此可证明式(95)是一守恒量.若 α=1,此时,时间尺度上的Lagrange 方程为 其守恒量为 在上述给出的初始条件下,当h=1和h=0.1 时,分别给出了q和I在时间段 [0,10]和 [0,3.5] 的模拟结果,如图4 所示. 图4 α=1 时 q 和 I 的值Fig.4 Simulation of qand Iwithα=1 将分数阶理论和时间尺度理论应用到动力学问题的研究中,建立的分数阶时间尺度模型更具有广泛的应用性、更切合实际问题.结合分数阶微积分和时间尺度微积分,我们研究了CaputoΔ型分数阶时间尺度Noether 定理.若 α=1,文献[31]在特殊无限小变换下得到的时间尺度Noether 定理与我们的定理1 一致,但其一般无限小变换下的Noether 定理却不能成为文中的定理2.利用文献[45]中的广义Jost 方法得到了一般无限小变换下的分数阶时间尺度Noether 定理,并通过算例验证了用该方法得到的守恒量是常数,验证了定理的正确性.进一步地说明了运用文献[31]中的时间重新参数化技术处理时间尺度Noether 定理是存在一些问题的. 分数阶时间尺度Noether 定理为求解复杂系统的方程提供了一种新方法,当然它还需要被进一步地研究和完善.在今后的工作中,还可考虑以下几个问题. (1) 研究如何将该方法进一步拓展到非完整系统和Birkhoff 系统或其他复杂动力学系统. (2) 本工作只研究了Caputo 型分数阶导数和Δ型时间尺度导数,也可研究其他分数阶导数和时间尺度导数以及它们之间的差异. (3) 在实际问题中,需要讨论分数阶时间尺度模型中Noether 守恒量的物理意义. (4) 值得注意的是,由于分数阶导数具有记忆性,一般算法并不适用于分数阶微积分,算例仅根据分数阶时间尺度积分和导数的定义进行计算的.分数阶时间尺度的保结构算法是一个新的、艰巨的领域,将是我们今后的主要工作.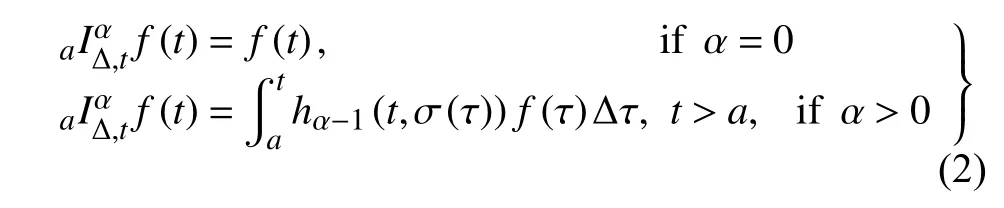
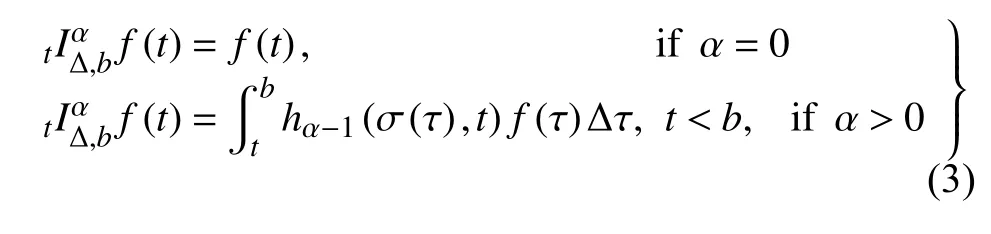
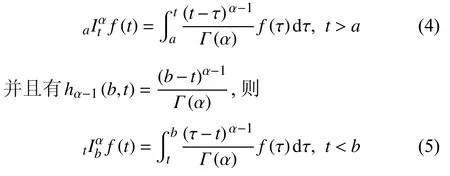


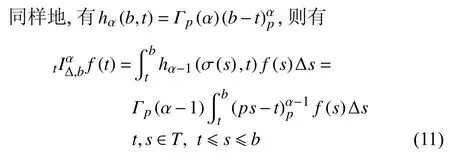
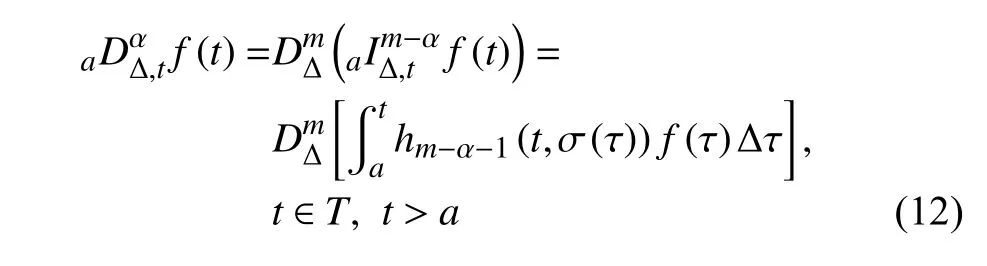

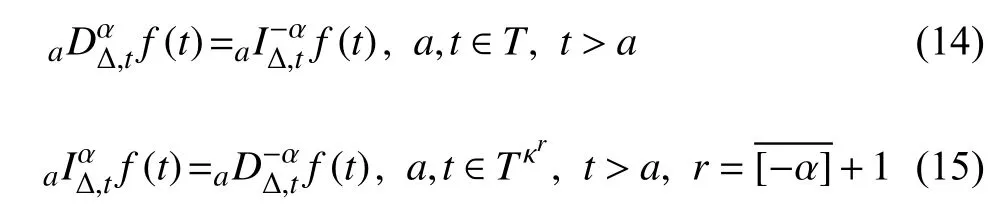
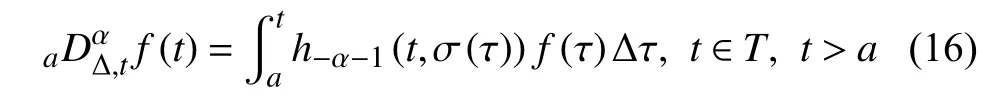
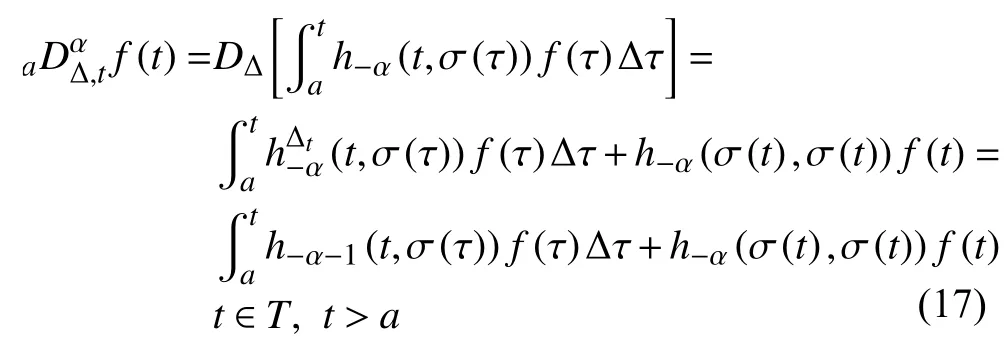
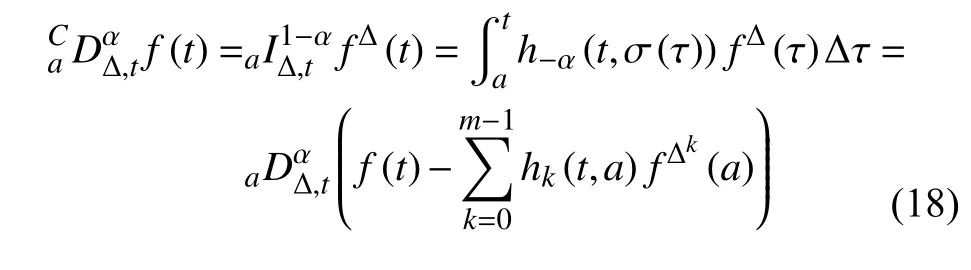
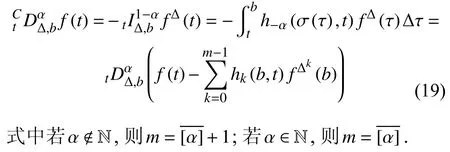


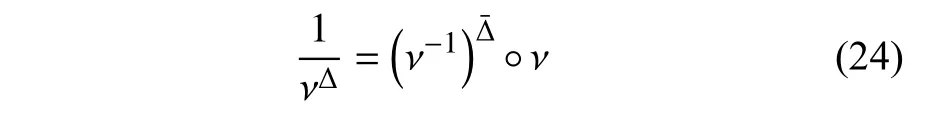


2 CaputoΔ型分数阶时间尺度Lagrange 方程



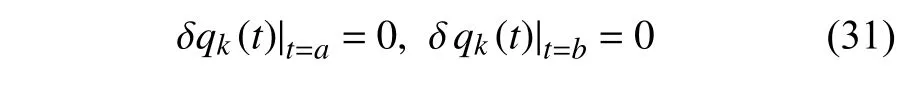
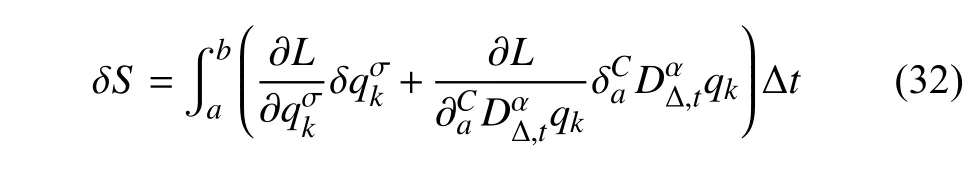

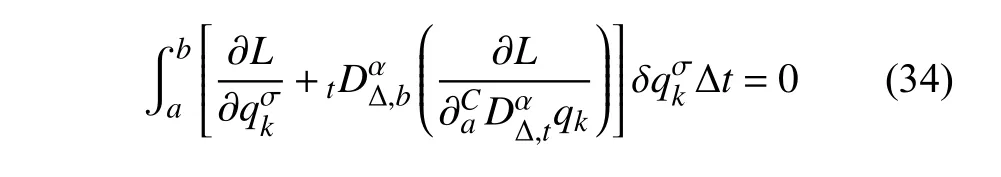

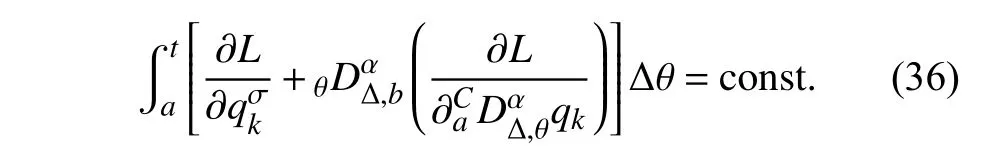
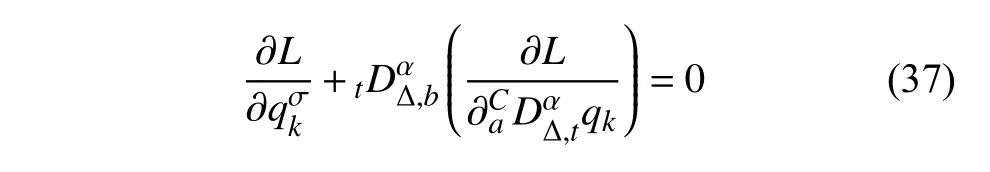
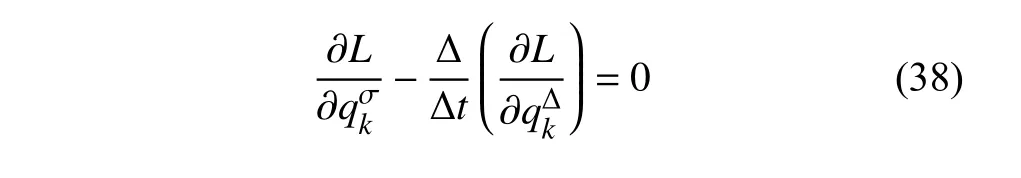


3 特殊无限小变换下的分数阶时间尺度Noether 定理

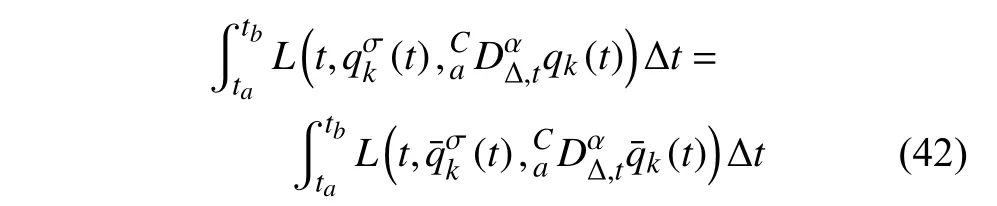
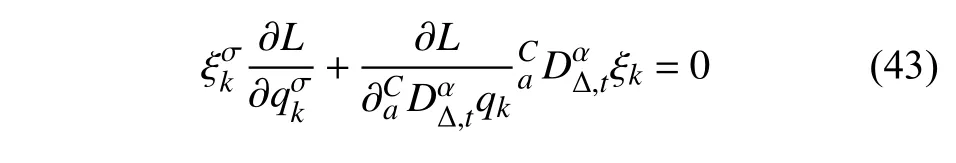
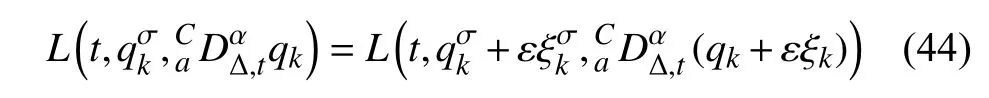



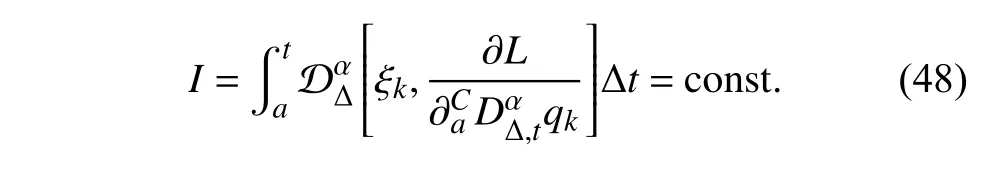

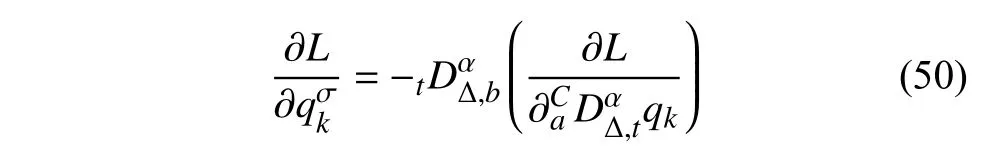
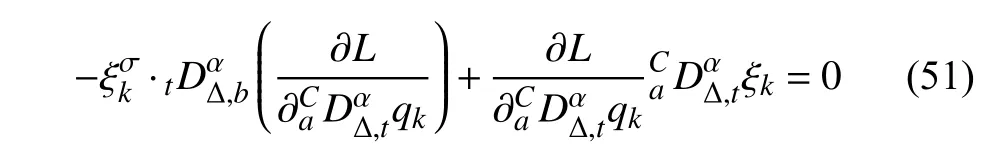
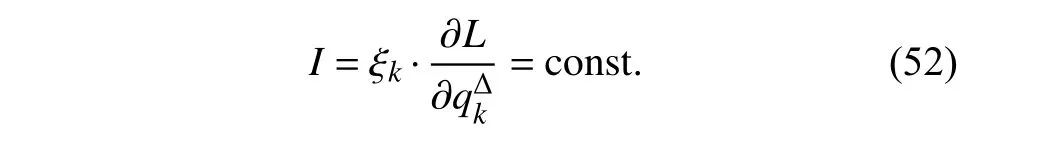
4 一般无限小变换下的分数阶时间尺度Noether 定理
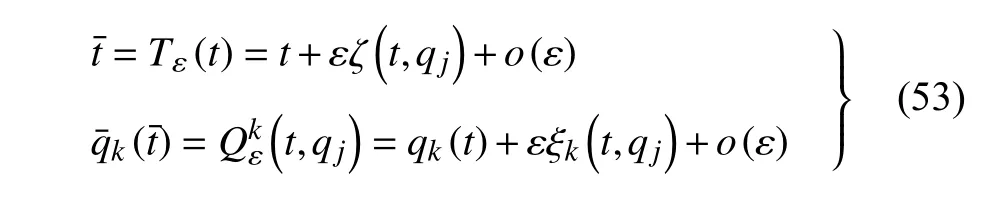

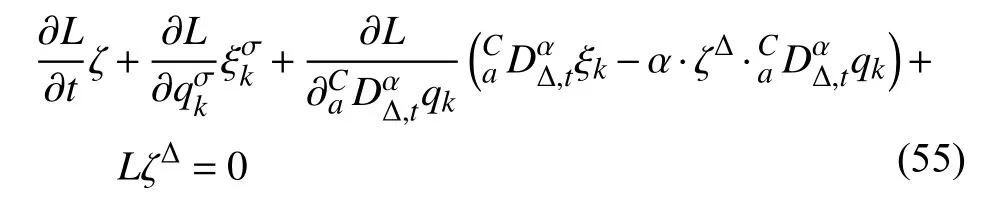


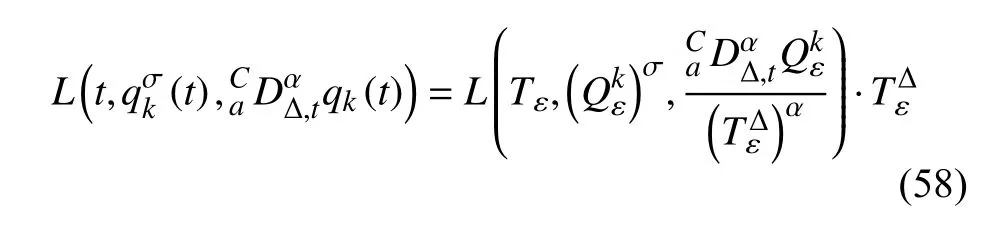
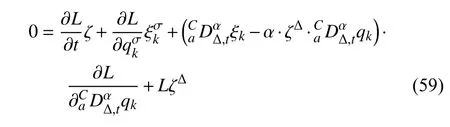


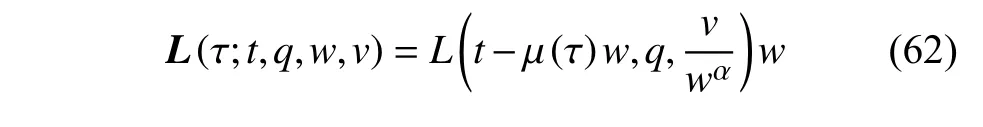
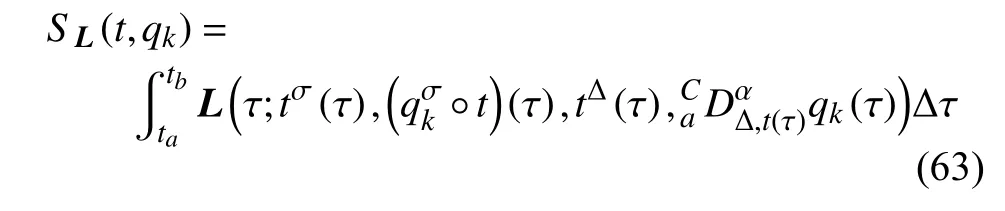
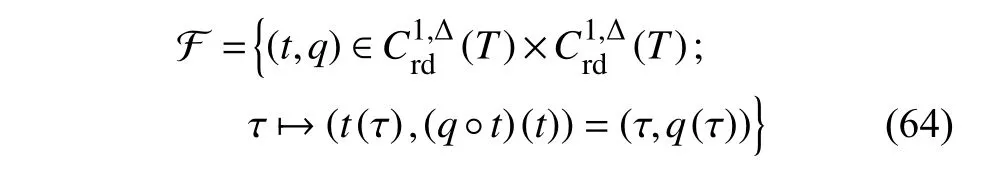
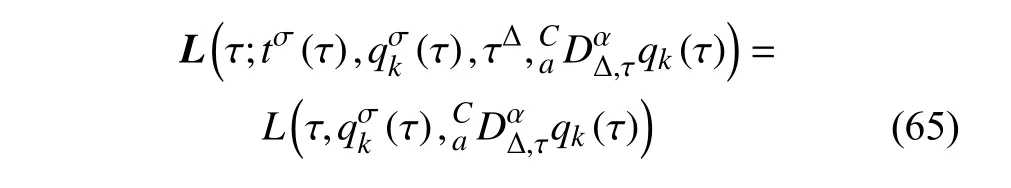



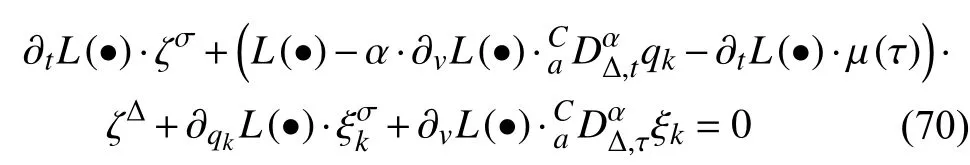



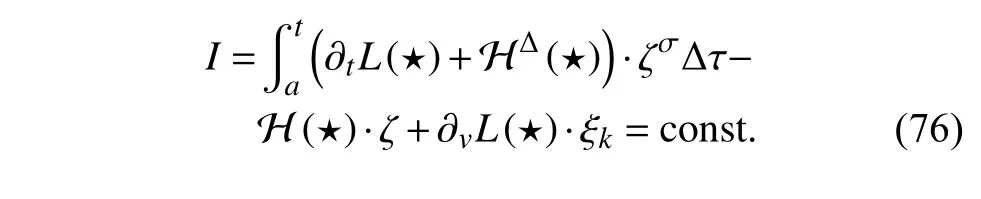
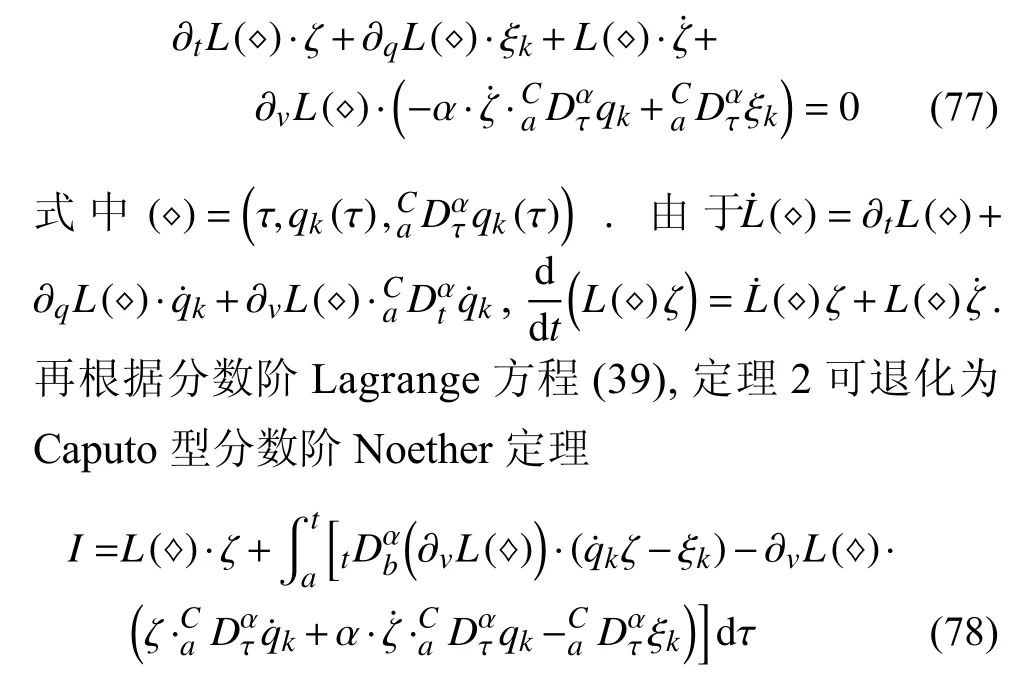
5 算例
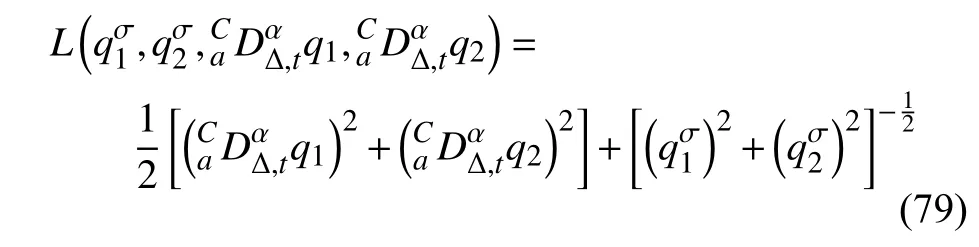
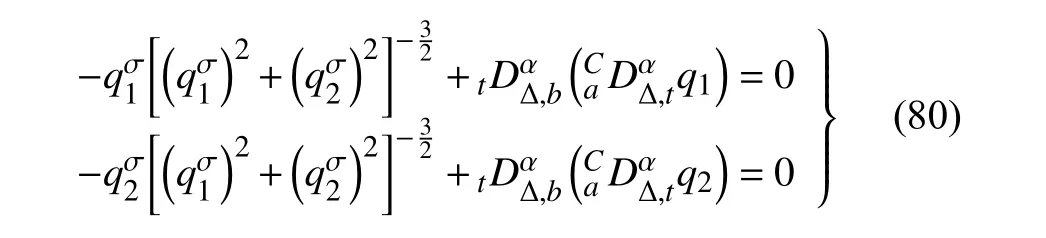


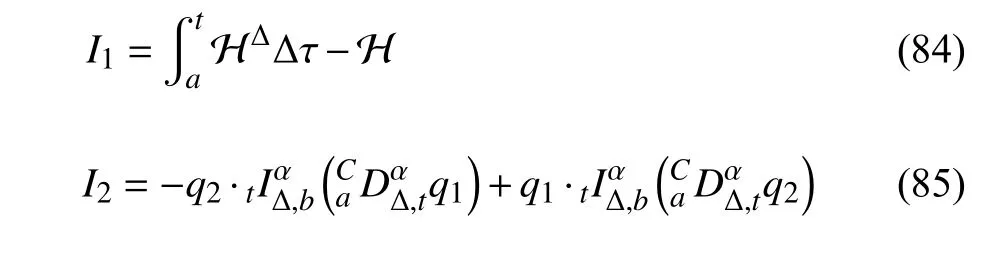
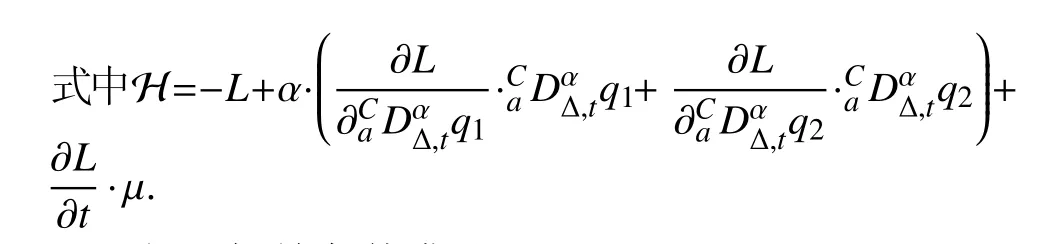
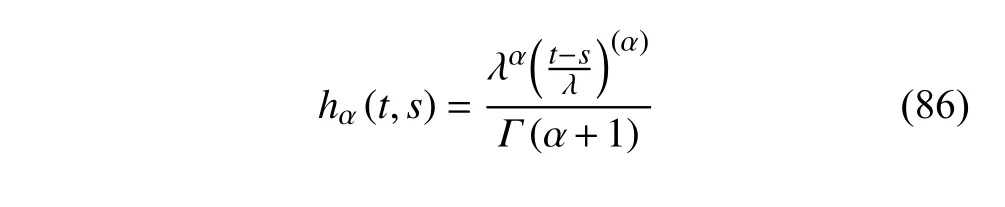

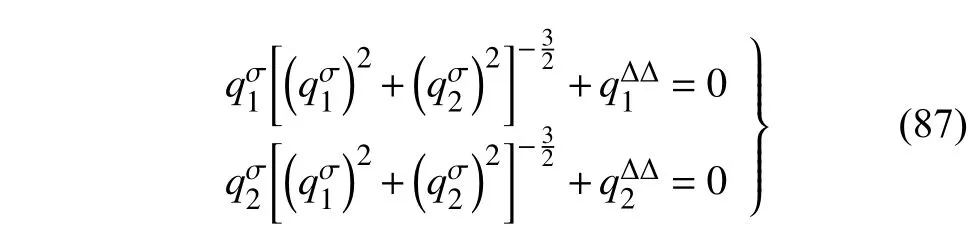
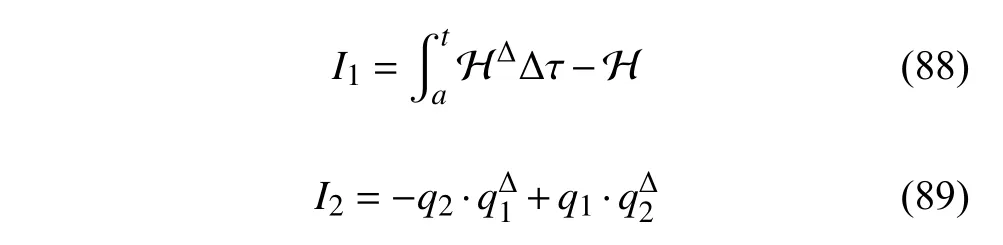


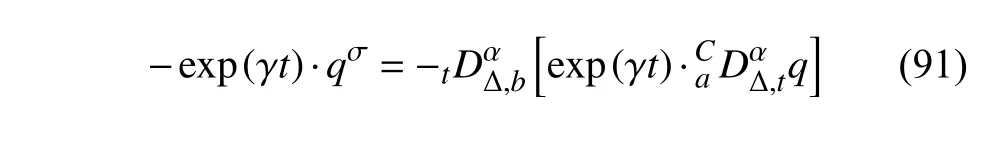
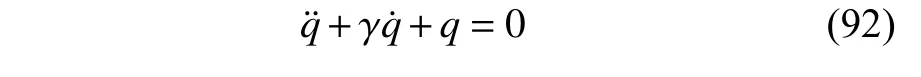

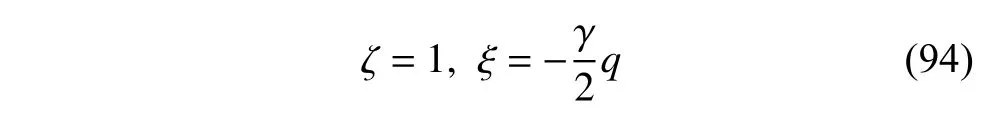
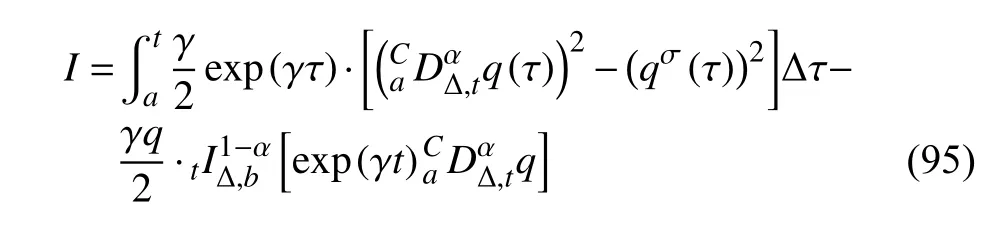
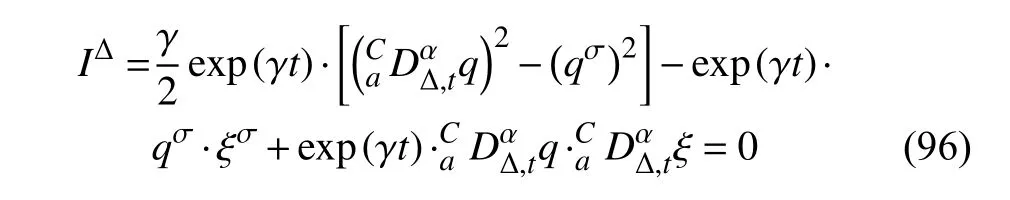
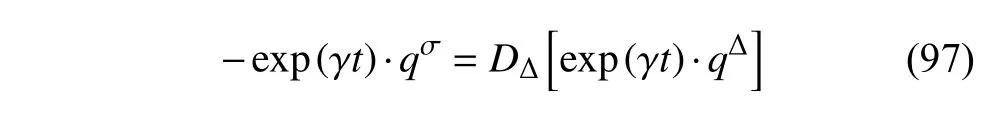

6 结论
