“触礁、穿越、影响”等问题的解法浅析

摘要：数学教学的一个重要任务是教学生数学建模，即如何将实际问题转化为数学问题，从而建立数学模型求解。“触礁、穿越、影响”等问题是生活中典型的实际问题，它们对应的数学实质是什么呢？本文通过实例分析、说明，归纳、介绍了这类问题的解题思路与方法。

关键词：实际问题;数学思想;解法

在学习了勾股定理、直角三角函数等知识后，解题中不时会遇到轮船航行中会不会触礁、修建高速公路会不会穿越保护区及大货车通过某路段时其噪声会不会影响学校教学等实际问题，学生由于不明白实际问题的数学意义，不能将“实际问题”转化为“数学模型”，往往不知所措，不得不依依不舍地放弃。

仔细分析总结触礁、穿越、影响等问题不难发现，虽然这些问题的表达形式不同，解题方法、过程也各有特点，但它们所蕴含的数学实质却是一致的，那就是“两理一法” 即“垂线段最短原理、勾股定理和比较法”的应用。只不过有的侧重于“长度比较”，有的侧重于“长度再应用”而已。同学们只要明白了这个实质，再掌握一些相关知識，如直角三角形性质（包括直角三角函数）、等腰三角形性等，解题时能综合应用，困难就会迎刃而解了。下面举例说明。

一、长度比较问题

这类问题的结论往往是：“会不会怎样？”的问法，如会不会触礁？能不能穿越？或会不会影响？等等实际问题，数学问题就是“长度比较”，即点到线的距离与已知半径比较，本质是求直角三角形的边长。方法一般是：首先，利用“垂线段最短”数学原理，过公园（或海岛）所在位置（点）作前进方向线所在直线的垂线，利用勾股定理及三角函数等性质求出垂线段的长;然后，将垂线段长与公园半径进行比较;第三，根据比较结果问答、解决问题，当垂线段长大于半径时，不会的; 当垂线长不大于半径时，会的。

例1、某地要修建东西走向的一条高速公路，工程行进到点A时，发现北偏东60的方向有一个小公园P，当公路修建向前推进10千米时到达点B时，测得公园正好在东北方向。中途由于资金问题高速公路修建停工了一年多，在此期间，随着人们健康意识提高和当地党委、政府的重视，小公园将扩建成半径为的15千米的圆形“主题健身公园”，试问，复工后高速公路再修建会影响“主题健身公园”吗？为什么？

分析：本题是一个实际问题，解决问题的关键是“会不会影响公园修建”这个实际问题对应的数学问题是什么呢？其实就是公路修建结束后公园还能不能按计划修建，也就是公园中心到高速路的距离是不是比公园的计划半径大的问题。这就转化成了“求点到直线的距离”，也就是求“长度”的数学问题了。

解：过点P作PC ⊥ AB，交AB的延长线于点C，如图，由题意得，∠PCA=90°，

∠PAC=90°-60°=30°，∠PBC=45°，所以，BC=PC，AP=2PC，由勾股定理得：AC=PC.

因为AC-BC=AB，AB=10，所以，PC-PC=10，解得，PC=5（  +1）=13.66，因为13.66<15，所以，会影响公园修建。

二、影响时间问题

这类问题往往是在前面问题基础上的进一步深化，数学实质是长度小于半径时，求公园等目标点为顶点，底边在前进方向线上腰长为公园半径的特殊等腰三角形的底边长，然后，再利用物理知识求时间。

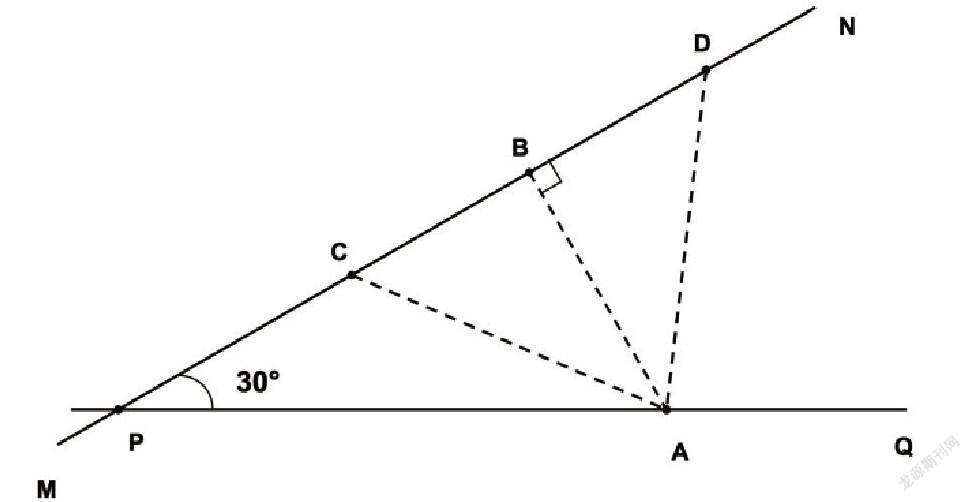
例2、如图，公路MN和PQ在点P处交汇，已知QPN=30，点A处有一所小学，AP=160米，假使拖拉机行驶时，周围100米内会受到噪音影响，那么拖拉机在公路上沿PN方向行驶时，学校是否受到噪音影响？若受影响，已知拖拉机的速度为18千米/小时，那么学校受影响的时间是多少？

分析：学校教学受到影响的条件是点A到公路MN的距离小于100，这个问题的解决首先要求出AB的长，才能作出判断;如果AB<100，就要考虑在直线MN上什么范围内的点到A的距离不大于100.于是，转化为研究特殊的等腰三角形底边计算。

解：过点A作直线MN的垂线AB，垂足为B，如图，由题意知，∠ABP=90°，∠APB=30°，AP=160，所以，AB=80，BP=80，因为80<100，所以学校教学分受到影响。设拖拉机行进至点C时影响开始，到点D时影响结束，如图，连接AC和AD。由题意得，AC=AD=100，而AB=80，所以由等腰三角形性质和勾股定理得BC=BD=60，所以CD=2BC=120，影响时间t=120/18=20/3小时=24秒。因此，学校受影响的时间是24秒。

作者简介：娄金智（1965-）男，贵州余庆人，本科，中学高级教师，研究方向：初中数学教学与解题研究.