数学建模复习教学探析
2021-03-19刘兴安
刘兴安

[摘 要] 概述数学建模的概念与价值,提出数学建模专题复习的教学策略,以使学生在操作体会的基础上,总结数学建模的一般步骤,并迁移应用在其他问题上,进而发展学生的数学核心素养.
[关键词] 数学建模;复习教学;初中数学
数学核心素养包括数学抽象、数学建模、数学运算等六大核心素养. 其中数学建模是中心,其是联系数学与外部世界的桥梁,也是运用数学的思维方式解决实际问题的重要工具.笔者尝试在学生操作体会的基础上,总结数学建模的一般步骤,并迁移应用在其他问题上,进而发展学生的数学核心素养.
数学建模的概念与价值
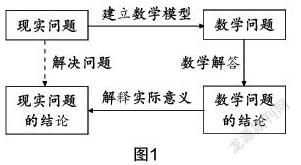
数学建模是指抽象现实问题,用数学语言表达,然后运用解方程、解不等式或函数的性质进行研究,得到数学问题的结论,最后用数学问题的结论解释实际问题,从而得到实际问题的结果[1].
数学建模的操作步骤:(1)分析现实问题;(2)根据现实问题的特征选择合适的数学模型;(3)应用数学中的定理、性质或法则等解答数学模型;(4)以数学模型的答案解释实际问题得到现实问题的解,如图1.
数学建模的价值:学习数学建模,可使学生认识到数学的应用价值,发展学生数学抽象、数学建模、数学运算与数据分析等核心素养,在分析问题与解决问题的过程实现数学的教育价值.
教学目标及解析
(1)教学目标:①通过具体实例,经历建立方程、不等式、函数模型的过程;②总结归纳建立方程、函数、不等式模型的一般过程,得到数学建模的一般步骤,感受数学建模的价值;③应用抽象出的数学建模的方法步骤解决新问题.
(2)教学目标解析:①完成第一个教学目标的标志是:在实际问题中,学生能够通过自主学习,发现方程、不等式、函数模型;②完成第二个教学目标的标志是:学生能够对数学建模解决现实问题的过程进行反思,总结得出数学建模的操作要领,深化学生对数学建模的认识;③完成第三个教学目标的标志是:在巩固训练中,学生能够自主运用数学建模解决问题[2].
教学问题诊断分析
(1)学生原有的基础:学生已经掌握了三种函数的概念、图像及性质,掌握了四种方程的概念、解法及应用,掌握了不等式的概念、解法及应用,对数学建模有了初步理解.
(2)存在困难:学生对数学建模的经验是零散的,没有形成体系,没有掌握其操作要领,没有应用数学建模解决问题的意识,什么情况下选择什么样的数学模型,学生没有认识.
(3)教学难点:根据现实问题选择合适的数学模型解决问题,突破难点的方法是以具体问题为背景,体会数学建模的价值,总结数学建模的方法和步骤,并通过适当的训练加以巩固.
数学建模专题复习的教学策略
1. 反思解决具体问题的过程,感受数学建模的思想和方法
案例1 由于新冠肺炎疫情暴发,某公司根据市场需求代理A,B两种型号的空气净化器,每台A型净化器比每台B型净化器进价多200元,用5万元购进A型净化器与用4.5万元购进B型净化器的数量相等.
(1)求每台A型、B型净化器的进价各是多少元.
(2)公司计划购进A,B两种型号的净化器共50台进行试销,其中A型净化器为m台,购买资金不超过9.8万元. 试销时A型净化器每台售价2500元,B型净化器每台售价2180元. 公司决定从销售A型净化器的利润中按每台捐献75元作为公司帮扶疫区贫困居民,设公司售完50台净化器并捐献扶贫资金后获得的利润为w,求w的最大值.
分析 (1)设每台B型净化器的进價是x元,则每台A型净化器的进价是(x+200)元,依题意得=,解得x=1800.经检验,x=1800是原方程的解,且符合题意,所以x+200=2000. 答:每台A型净化器的进价是2000元,每台B型净化器的进价是1800元.
(2)因为购进A型净化器m台,所以购进B型净化器(50-m)台,又购买资金不超过9.8万元,所以2000m+1800(50-m)≤98000,所以m≤40. 依题意,获得的利润w=(2500-2000-75)m+(2180-1800)(50-m)=45m+19000. 因为45>0,所以w随m的增大而增大,所以当m=40时,w取得最大值,最大值是45×40+19000=20800. 答:w的最大值为20800元.
设计意图 原题叙述中存在等量关系,即“用5万元购进A型净化器与用4.5万元购进B型净化器的数量相等”,应建立方程模型求未知数;在第二小题的题意中有不等关系,即“购买资金不超过9.8万元”,应建立不等式的模型求参数m的取值范围;求利润的最大值,应建立函数关系利用函数的增减性解决,其是建立函数模型的标志性信息.
2. 通过归纳推广,抽象数学建模的一般思想和方法
让学生分别回顾并反思建立方程模型、建立不等式模型、建立函数模型解决问题的过程,如图2、图3、图4所示,引导学生总结归纳共性,最后得到数学建模的一般操作步骤.即首先要分拣出相关的量,分析相关量之间的数量关系;然后选择数学模型,并根据数量关系建立模型,从而转化为数学问题;最后解方程或不等式,化简函数解析式,利用函数性质解答,从而得到实际问题的答案. 其关键步骤是:分析相关量之间的数量关系,选择数学模型[3].
3. 在迁移应用中,巩固数学建模的数学思想
案例2 如图5,在一平直的河岸l同侧有A,B两村. A村位于河流l正南4 km,B村位于A村东8 km南7 km处. 现要在河岸边建一水厂C为两村供水,要求管道长度最少,请你确定选址方案,并求出所需最短管道的长度.
分析 第一步,分析问题的构成要素.即在已知直线l的同侧有两个固定点A,B,其目的是在已知直线上找一点C,使它们构成的单向线段和最小,这里需要把两个村庄抽象为两个点,把河流抽象为直线,这样就把实际问题转化为数学问题了.
第二步,此问题应分成两种情况加以研究,即A,B之间有线段连接时,包括两种情况:第一种,如图6所示,显然图6的第二个图管道长度比较长,应舍去. 图6中第一个图的管道长度计算如下:连接AB,过A作AC1⊥l于C1,则C1即为水厂地址;过B作BD⊥AC1交C1A的延长线于D,则AD=7 km,BD=8 km,AC1=4 km,所以AB==(km),所以所需管道的长度是AC1+AB=(4+) km. 第二种情况是在A,B之间没有线段相连时,如图7所示,作A关于直线l的对称点A′,连接A′B交直线l于C2,则C2即为水厂地址. 过B作BD⊥AA′交A′A的延长线于D,则A′D=15 km,BD=8 km,所以所需管道的长度是A′B==17 km.综上所述,所需最短管道的长度是(4+) km.
设计意图 迁移应用属于高阶思维能力,从方程、不等式、函数模型,应用几何模型解决了现实问题,巩固了数学建模的数学思想.在先分类再整合的过程中,学生积累了分析问题、解决问题的经验,应用总结出的数学建模的思想和方法解决了新问题,实现了数学建模思想的迁移,拓宽了数学建模的应用领域.
总之,培养学生的数学建模素养,能够让学生体会数学的实用价值,激发学生的学习数学的内驱力,提高学生思维的灵活性,提升学生发现问题与解决问题的能力.
参考文献:
[1]邱宗如. 初中数学模型思想的教学实践与思考[J]. 福建中学数学,2020(08).
[2]吴香秀. 培养数学建模能力 落实数学核心素养[J]. 初中数学教与学,2020(10).
[3]王秀秀,董磊,陈棉驹. 初中数学模型思想方法的内涵及教学分析[J]. 中学数学教学参考,2019(11).
3190501908280
