“有理数加法”教学设计与反思

李中阳

[摘  要] 以“有理数加法”为例，立足生活实际，通过探究活动，引导学生总结归纳有理数加法法则，同时，在设计中，渗透分类讨论、数学结合等数学思想，培养学生直观想象、数学抽象、数学运算等核心素养.

[关键词] 有理数;加法;教学设计;反思

教学内容及解析

本节课是人教版七年级上册第1章第三节“有理数加法”第1课时的内容. 有理数的运算是有理数运算的起点，是小学非负数加法的拓展，又是有理数减法、乘法、除法的基础. 对于后面学习实数、代数式运算、解方程或不等式等都有帮助. 其中包含的数学思想方法对后续学习也有作用[1].

有理数加法有较强的生活价值，反映了数学来源于生活又高于生活. 学生应掌握和理解有理数加法运算的思维方式，即先确定结果的符号，再确定结果的绝对值. 鉴于此，本节课的重点应为：理解有理数加法的合理性.

教学目标及解析

教学目标：（1）理解与识记有理数加法法则;（2）能直接运用有理数加法法则进行简单的计算;（3）在探索有理数加法法则的过程中，感受分类讨论、数学归纳和数形结合的数学思想[2].

目标解析：（1）能利用不同的问题情景解释有理数加法的不同情况，如“负数+负数”用物体先向左运动再向左运动来解释;（2）对于两个有理数相加，能依据有理数加法法则进行计算;（3）物体在数轴上运动，根据运动步数与方向写出对应加数，根据终点的位置写出对应结果.

教学问题诊断解析

学生在小学阶段已学习了正数+正数，正数+0的运算，进入初中后学生又学习了负数、数轴与绝对值等知识，这些知识都是学习有理数加法的基础知识. 当数系扩大后，加法的含义发生了变化，相同或相反意义的量都可以相加，这对于学生来说有一定的困难.

七年级学生已具有观察、猜想的能力，还有一定的合作交流能力，但是由于学生的思维水平有限，知识储备不够，所以有理数的加法应分几种情况，如何归纳各种情况，教师需要做适当的引导，特别对于绝对值不等的异号两数相加，学生理解有一定的难度. 基于此，本节课的难点确定为：理解异号两数相加的法则[3].

教学过程设计

1. 创设情境，引出新课

情境1：原来的温度是-4 ℃，上升7 ℃后的温度是多少呢？

情境2：小明中午支出20元，下午又收入90元，那么小明今天结余多少钱呢？

教师：生活中存在具有相反意义的量，我们可以用正数、负数表示，当这些量依次发生变化时，可以用有理数加法表示，如上述两个情境可以分别用-4+7，-20+90表示，这些算式的结果是多少呢？今天让我们一起来探究有理数的加法.

设计意图：根据生活实际，获取有理数加法的数学模型，提出问题：如何计算它们的结果呢？引发学生思考，顺利进入下一个环节.

2. 观察探究，总结法则

教师：在小学已学习了正数+正数，正数+0，当引入负数之后，有理数加法还会有哪些情况出现呢？

学生：正数+负数，负数+正数，负数+负数，负数+0.

追问：上述六种情形，从大的方面可以分成几种类型呢？

师生活动：在教师的引导下，师生将上述六种情况归纳为三种情况：相同符号的两数相加，不同符号的两数相加，一个数与0相加.

设计意图：在引入新数即负数之后，有理数的加法运算也产生了新的变化，学生能列出有理数加法的六种情况，但是把这六种情况归类成三种类型，学生存在一定的困难，需要教师的耐心引导与总结.

探究1：一只蚂蚁在一条直线上向左或向右运动，设定向右为正，向左为负. 如果蚂蚁先向右运动5米，再向右运动3米，那么这只蚂蚁两次运动的结果是向哪个方向，运动了多少米？用算式如何表示呢？

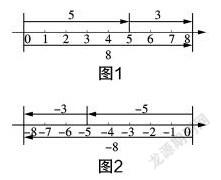
教师首先让学生从数的视角分析运动过程，然后，教师引导学生从形的角度表示蚂蚁的运动过程，如图1所示.

设计意图：七年级学生以形象思维为主，以具体可感的生活问题解释有理数的加法，有理数加法的合理性得到了解释，教师从数与形两个角度加以引导，渗透了从特殊到一般的数学思想.

探究2：一只蚂蚁先向左运动5米，再向左运动3米，那么两次运动后，蚂蚁向哪个方向运动，运动了多少米？用算式如何表示这个过程呢？

师生活动：学生先独立思考，然后，在教師的引导下，学生要明白两次运动的相互关系，如何用算式表示这个过程.

追问1：算式（-5）+（-3）=-8，结果合理吗？其中的负号与绝对值分别代表了什么？

追问2：请从符号与绝对值两个角度考虑，概括相同符号的两个数相加的情形.

设计意图：此探究是为了说明“负数+负数”的情形与“正数+正数”的情形类似，两种情形综合，学生容易得出同号两数相加的有理数加法法则. 教师重在从研究思路上引导学生总结，渗透了从特殊到一般的思想方法.

探究3：（1）一只蚂蚁先向左运动3米，然后向右运动5米，那么这只蚂蚁最终向哪个方向运动，运动了多少米？请用算式表示这个过程.

（2）一只蚂蚁先向右运动3米，然后向左运动5米，那么这只蚂蚁最终向哪个方向运动，运动了多少米？请用算式表示这个过程.

学生：第一只蚂蚁最终运动结果为向右运动了2米，用算式表示为（-3）+（+5）=+2;第二只蚂蚁最终运动结果为向左运动了2米，用算式表示为（+3）+（-5）=-2.

追问1：根据前面的活动经验，从有理数的符号与绝对值两个视角，你能概括符号不同的两个有理数相加的法则吗？

追问2：如是这只蚂蚁先向右运动10米，再向左运动10米，那么这只蚂蚁向哪个方向运动，运动了多少米？如何用算式表示这个过程呢？

设计意图：利用数轴验证有理数加法的意义，体现了数形结合的数学思想，用形象直观的方法验证了有理数加法的合理性，突破了难点. 提高了学生直观想象、数学抽象的核心素养.

教师：如果一只蚂蚁第一段时间向左运动12米，第二段时间原地不动，那么这只蚂蚁最终向哪个方向运动，运动了多少米？用算式如何表示这个过程呢？

设计意图：此实例旨在引出一个数与0相加的情形.

此时，师生共同总结有理数加法法则：（1）同号两数相加，符号取与加数相同的正负号，然后把绝对值相加;（2）绝对值不相等的异号两数相加，符号取绝对值较大加数的符号，然后用较大的绝对值减去较小的绝对值;（3）互为相反数的两个数相加，其和为0;（4）任何一个数与0相加，仍得这个数.

设计意图：在探究过程中，学生会发现这样一种变化，即有理数运算的结果，不仅要考虑结果的符号，而且要考虑结果的绝对值. 这种思维方式在向量运算、力的合成运算中都有体现.

3. 典例演练，巩固新知

例：计算：（1）（-9）+（-7）;（2）（-9.2）+3.8;（3）0+（-2020）;（4）（-100）+100.

学生：（-9）+（-7）=-（9+7）=-16. （同号两数相加，符号取与加数相同的正负号，然后把绝对值相加）

学生：（-9.2）+3.8=-（9.2-3.8）=-5.4. （绝对值不相等的异号两数相加，符号取绝对值较大加数的符号，然后用较大的绝对值减去较小的绝对值）

学生：0+（-2020）=-2020. （任何一个数与0相加，仍得这个数）

学生：（-100）+100=0. （互为相反数的两个数相加，其和为0）

师生活动：总结两个有理数相加的运算步骤，（1）判断是同號、异号、互为相反数，还是其中一个为0;（2）确定结果的正负号;（3）将它们的绝对值实施加减运算.

教学反思.

1. 重建加法概念

按照有理数加法法则进行运算，并不是一件难事，但是让学生理解并接受有理数的加法法则十分困难，为此，本节课引入了蚂蚁在直线爬行的实例，让学生直观感受有理数的加法法则的建立过程.

2. 有理数加法法则实际是将其转化为小学数学的加减法运算

根据有理数的加法法则，不难发现，当结果确定了符号之后，接下来进行的就是小学学过的正数或0的加减法运算，所以确定结果的正负号是本课的重头戏.

3. 数学思想方法的真落实

数学教学不仅要教授学生知识，而且要让学生掌握思想方法，然后用这些思想方法指导今后的学习与生活. 本节课渗透了数形结合思想、转化思想等，培养了学生数学抽象、直观想象等核心素养.

参考文献：

[1]李冰冰，王洁. 渗透数学思想  培养运算能力——以沪科版“有理数的加法”教学为例[J]. 教育文汇，2019（12）.

[2]杨慧园. 有理数加法法则的探索[J]. 中学数学教学参考，2019（23）.

[3]贾京周. 基于初中数学核心素养的有理数加法教学探究[J]. 新教育，2017（34）.

3218501908283