统计与概率在生活中的运用

郭英

我们的生活离不开数学。统计与概率是数学知识的重要组成部分，其在生活中的应用是广泛而有意义的。

一、统计知识的运用

例1 （2020·江苏淮安）为了响应市政府创建文明城市的号召，某校调查学生对市“文明公约十二条”的内容了解情况，随机抽取部分学生进行问卷调查。问卷共设置“非常了解”“比较了解”“一般了解”“不了解”四个选项，分别记为A、B、C、D，根据调查结果绘制了尚不完整的统计图如下。

市“文明公约十二条”了解情况条形统计图

请解答下列问题：

（1）本次问卷共随机调查了学生，扇形统计图中C 选项对应的圆心角为度;

（2）请补全条形统计图;

（3）若该校有1200名学生，试估计该校选择“不了解”的学生有多少人。

解：（1）24÷40%=60（名），360°× 1860=108°。

故答案为60名，108。

（2）60×25%=15（人）。

补全条形统计图如图所示：

市“文明公约十二条”了解情况条形统计图

（3）1200× 360=60（人）。

答：该校1200名学生中选择“不了解”的有60人。

【点评】本题考查了条形统计图和扇形统计图的综合运用，是一种经典题型。解这类问题一般是先从两幅统计图中找出数值都已知的项目，如本题中的B项，B項有24人，占样本总数的40%，用24÷40% 即可求出样本容量，接下来补全条形图就迎刃而解了。最后一问考查的是用样本的情况来估计总体的情况。

例2 （2020·江苏泰州）2020年6月1日起，公安部在全国开展“一盔一带”安全守护行动。某校小交警社团在交警带领下，从5月29日起连续6天，在同一时段对某地区一路口的摩托车和电动自行车骑乘人员佩戴头盔情况进行了调查，并将数据绘制成如下图表：

2020年6月2日骑乘人员头盔佩戴情况统计表

2020年5月29日—6月3日骑乘人员头盔佩戴率折线统计图

（1）根据6月3日的数据，小明认为该地区全天摩托车骑乘人员头盔佩戴率约为95%。你是否同意他的观点？请说明理由。

（2）相比较而言，你认为需要对哪类人员加大宣传引导力度？为什么？

（3）求统计表中m 的值。

解：（1）不同意，虽然通常可用某地区一路口的摩托车骑乘人员佩戴头盔情况来估计该地区的摩托车骑乘人员佩戴头盔情况，但是，这里只用6月3日的来估计，具有片面性，不能代表该地区的真实情况，可用该地区一路口一段时间内的平均值进行估计，就比较客观、具有代表性。

（2）通过观察折线统计图中摩托车和电动自行车骑乘人员佩戴头盔的百分比的变化情况，可以得出：需要对电动自行车骑乘人员加大佩戴头盔宣传引导的力度，因为在这些天，电动自行车骑乘人员佩戴头盔的百分比增长速度较慢，且不足50%。

（3）由题意得7272 + m=45%，

解得m=88。

经检验，m=88是分式方程的解，且符合题意。

答：统计表中的m 的值为88。

【点评】本题考查的是统计表与折线统计图的综合运用，考查了同学们的读图能力。折线统计图是三种常见统计图之一，它的优点是可以反映数据的变化情况和发展趋势。解题时，同学们如果抓住这一特点去分析问题，就能很容易地找到第（2）问的答案。

二、概率知识的运用

例3 （2020·江苏连云港）从2021年起，江苏省高考采用“3+1+2”模式：“3”是指语文、数学、外语3科为必选科目，“1”是指在物理、历史2科中任选1科，“2”是指在化学、生物、思想政治、地理4科中任选2科。

（1）若小丽在“1”中选择了历史，在“2”中已选择了地理，则她选择生物的概率是

;

（2）若小明在“1”中选择了物理，用画树状图的方法求他在“2”中选化学、生物的概率。

解：（1）在“2”中已选择了地理，从剩下的化学、生物、思想政治三科中选一科，因此选择生物的概率为13。

故答案为13。

（2）用画树状图法表示所有可能出现的

结果如下：

共有12种可能出现的结果，它们都是等可能的，其中选中化学、生物的有2种，

∴P（化学生物）= 2/12=1/6。

【点评】用画树状图法求事件发生的概率是中考必考的内容，同学们需要仔细审题，理解题意，画出完整的树状图，才能轻松解决概率题。

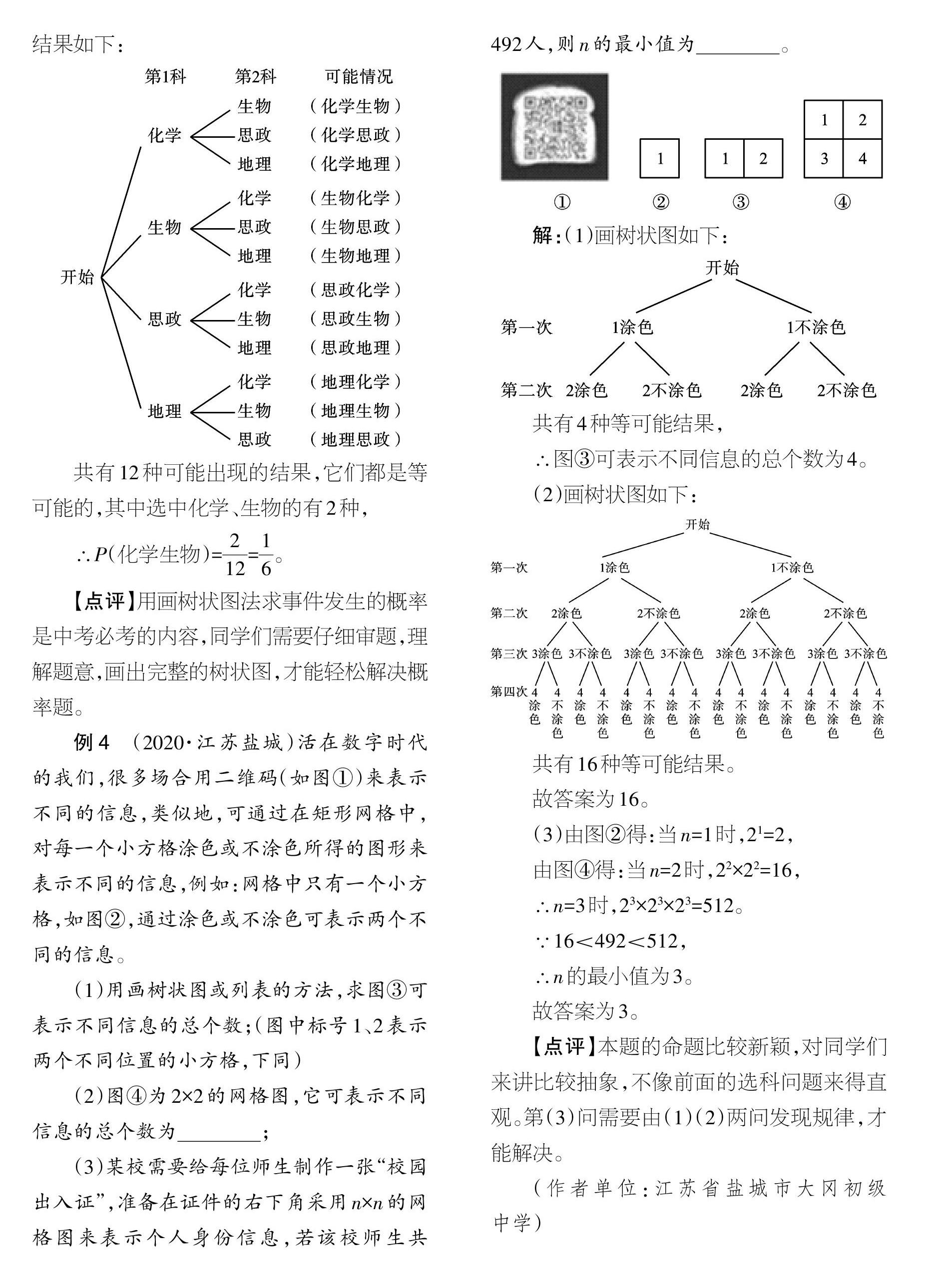
例4 （2020.江苏盐城）活在数字时代的我们，很多场合用二维码（如图①）来表示不同的信息，类似地，可通过在矩形网格中，对每一个小方格涂色或不涂色所得的图形来表示不同的信息，例如：网格中只有一个小方格，如图②，通过涂色或不涂色可表示两个不同的信息。

（1）用画树状图或列表的方法，求图③可表示不同信息的总个数;（图中标号1、2表示两个不同位置的小方格，下同）

（2）图④为2x2的网格图，它可表示不同信息的总个数为____;

（3）某校需要给每位师生制作一张“校园出入证”，准备在证件的右下角采用nXn的网格图来表示个人身份信息，若该校师生共492人，则n的最小值为

。

解：（1）画树状图如下：

共有4种等可能结果，

∴图③可表示不同信息的总个数为4。

（2）画树状图如下：

共有16种等可能结果。

故答案为16。

（3）由图②得：当n=l时，21=2，

由图④得：当n=2时，22x22=16.

∴n=3时，23x23x23=512.

∵16<492<512.

∴n的最小值为3。

故答案为3。

【点评】本题的命题比较新颖，对同学们来讲比较抽象，不像前面的选科问题来得直观。第（3）问需要由（1）（2）两问发现规律，才能解决。

（作者单位：江苏省盐城市大冈初级中学）