核心素养视角下初中数学变式教学

[摘要]在初中数学教学中，教师应积极改变传统“就题论题”等教学理念，秉持不变性、适当性、递进性原则，抓数学问题的本质，引导学生体会知识的发生、发展过程，并鼓励学生自我反思、总结、归纳和提炼，最终达到提高初中数学教育综合质量，培养学生核心素养的目的

[关键词]核心素养;初中数学;变式教学

作者简介：沈云（1981-），本科学历，中小学一级教师，从事初中数学教学工作.

教学初中数学多年，笔者发现相当数量的学生常常陷人题海战术的怪圈在解析数学问题时易受某种框架的束缚，显然，这种现象的存在既不利于学生深度探究，也不利于学生核心素养的培养，而变式教学可以不断调整学生的思维，让学生在变化的情境中综合运用比较、归纳、演绎等方式深化认识，有效归纳、总结出每个知识点之间的内在联系，从而达到培养学生核心素养的目的

核心素养视角下初中数学变式教学策略

1.变化非本质条件，充分调动学生的积极性

为了凸显教学重难点，教师应在不改变原有题目本质的基础上，不断改变题目背景、假设等非本质条件，从而促使学生依照所学数学内容，形成符合自身解题刁惯的数学思维体系.例如，在组织学生探究“利用相似三角形测高”知识时，笔者不断改变原有题目的题设条件和问题呈现方式，引导学生依照三角形相似性质，通过构建不同辅助线的方式展开自主探究，从而达到培养学生数形建模、直观想象、数据分析等核心素養的目的.

2.特殊条件一般化，赋予题目全新表现形式

同类的数学问题具有相似的解题思路，教师应从学生的认知角度出发，不断转变原有题目中的特殊条件，使已知条件更加普遍，并不断归纳与总结解题经验，达到多题归一的目的.例如，在组织学生探究“利用相似三角形测高”知识时，笔者呈现了A同学站立于旗杆影子顶端处的特殊情形，且为使学生的数学思维更加活跃，笔者根据日常生活实际，创设了旗杆的影子恰好落在其他建筑物上、旗杆的影子落到与地面夹角成a的斜坡上等一般化变式场景.显然，这种由特殊到一般的条件变式教学，能促使学生与教师形成高效交互，达到培养学生数学分析、逻辑推理、知识迁移等核心素养的目的

3.数学问题生活化，凸显变化实效性作为变式教学方法的核心，变化应积极与学生学习的需求成正比，并将数学问题生活化，促使学生主动融入学习氛围之中.例如，在组织学生探究“利用相似三角形测高”知识时，教师可以在学习完相关知识后，以测量实际生活中的某一建筑物高度为例，要求学生以小组的形式设计实施方案，并实地测量测算，从而达到培养学生数学应用、创新意识等核心素养的目的

核心素养视角下初中数学变式教学实践

仅有相关理论不能达到培养学生核心素养的目的.“利用相似三角形测高”是初中数学“图形的相似”章节中的主要内容，并且该知识点多次出现在中考中，在一定程度上具有形态各异的变式和丰富的研究价值，因此，为了研究的深入，笔者以“利用相似三角形测高”题多变为例进行探究.

1.原题探析

 如图1，A同学站立于旗杄影子的顶端处，已知同一时刻A同学的身高、A同学的影长、旗杄影长，试求旗杆的高度.

设计意图该题较好地考查了学生应用数学知识的技能和获得数学知识的思维，对初中生而言，此题属于中难度试题，主要考查图形相似等知识.具体解析该问题时，可以将试题抽象为如图2所示的形式，并根据相似性质得到

2.变式拓展

变式1如图3所示，已知具有刻度的某一标杆物，使旗杄顶端、标杆顶端以及A同学的眼睛恰好处于同一条直线上.若能获得A同学脚至旗杆底端、标杆底端的距离，以及A同学眼睛至脚底、标杆的高度等数据，试求旗杆的高度

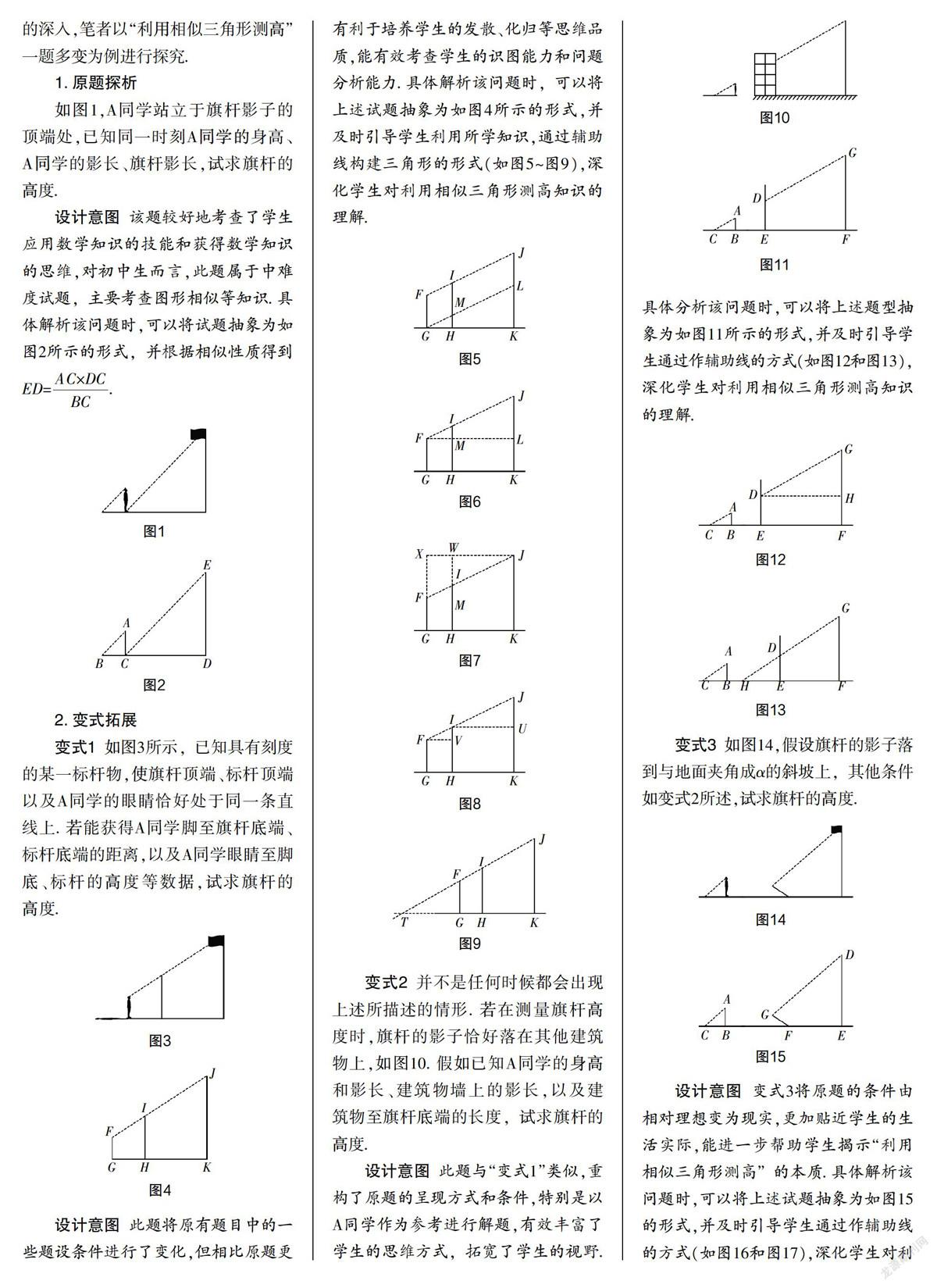
设计意图此题将原有题目中的些题设条件进行了变化，但相比原题更有利于培养学生的发散、化归等思维品质，能有效考查学生的识图能力和问题分析能力.具体解析该问题时，可以将上述试题抽象为如图4所示的形式，并及时引导学生利用所学知识，通过辅助线构建三角形的形式（如图5～图9），深化学生对利用相似三角形测高知识的理解.

变式2并不是任何时候都会出现上述所描述的情形.若在测量旗杄高度时，旗杆的影子恰好落在其他建筑物上，如图10.假如已知A同学的身高和影长、建筑物墙上的影长，以及建筑物至旗杄底端的长度，试求旗杆的高度.

设计意图此题与“变式1”类似，重构了原题的呈现方式和条件，特别是以A同学作为参考进行解题，有效丰富了学生的思维方式，拓宽了学生的视野.

具体分析该问题时，可以将上述题型抽象为如图11所示的形式，并及时引导学生通过作辅助线的方式（如图12和图13），深化学生对利用相似三角形测高知识的理解.

变式3如图14，假设旗杆的影子落到与地面夹角成a的斜坡上，其他条件如变式2所述，试求旗杆的高度.

设计意图变式3将原题的条件由相对理想变为现实，更加贴近学生的生活实际，能进一步帮助学生揭示“利用相似三角形测高”的本质.具体解析该问题时，可以将上述试题抽象为如图15的形式，并及时引导学生通过作辅助线的方式（如图16和图17），深化学生对利用相似三角形测高知识的理解

3.感悟提升

通过以上变式练习，学生熟练掌握了“利用相似三角形测高”的本质，教学时可在此基础上要求学生思考以下问题

（1）原式与变式在解法方面有什么关系？主要应用了哪些所学知识？原式还可以变成哪些题目？

（2）在实际问题中，请你想一想如何求解无法直接测量物体高度的问题.

（3）假设仅有一把测量尺，试利用所学知识设计出求解某一建筑物高度的方案

核心素养视角下初中数学变式教学反思

实质上，一道题目之所以具有变式价值，或许是解决该题目所应用的方式非常巧妙，或许是所涉及的知识点异常重要，而变式教学的目的是“以不变应万变”，让学生在掌握重要知识点的基础上发散思维.在变式教学中，教师应充分利用学生对变式教学的好奇心挖掘题目中的隐含条件和问题本质特征，让学生在非本质特征的变化中认识不变的规律，从而达到举一反三的学习效果.

同时，初中数学变式教学并不是越变”效果越好，不能即兴发挥，随心所欲地变.具体教学时，教师还应注重适当性原则，即知识跨度、难易程度要适当.若变化的复杂程度超出了学生的理解程度，则不仅不能发挥变式教学的作用，反而会削减学生学习的积极性，无法达到提升学生思维能力的目的.设计的变式题以2～4道为宜，附加考査的内容不能偏离课堂主线

此外，简单的题目能让学生获得成

就感和自信心，特殊化的题目方便展示规律，在具体的变式教学中，教师还应按照先易后难、从特殊到一般的原则，为学生提供解题思路或渗透某种思想方法，从而达到培养学生直观想象、逻辑推理等核心素养以及独立思考能力的目的到

总之，核心素养视角下的初中数学变式教学可以让学生在无穷的变化中领略数学知识的魅力.教师应积极改变传统“就题论题”等教学理念，秉持不变性、适当性、递进性原则，抓住数学问题的本质，引导学生体会知识的发生、发展过程，并鼓励学生自我反思、总结、归纳和提炼，最终达到提高初中数学教学综合质量、培养学生核心素养的目的.

参考文献：

[1]童晓杰.核心素养理念下的高中数学变式教学[J].名师在线，2018（7）

[2]姜炜.以变显质，谈初中数学的变式训练[J].数学教学通讯，2019（11）

[3]黄亚奇.以“变”促教，引领高效教学——一例析初中数学变式训练的实施策略[J].数学教学通讯，2019（2）