基于投影的不确定型多属性群决策的Dice相似度法

周文坤

（上海大学 管理学院，上海 200444）

0 引言

随着科学技术的发展和信息技术的推进，决策问题日益成为社会与经济生活的重要内容之一，并且呈现出决策参与者越来越多的群体化特征，以及表达决策的信息具有很大的不确定性。由于客观事物的复杂性和不确定性以及人类思维的模糊性，在群体决策过程中决策者往往不能明确地给出属性的权重信息，而给出的属性值是区间数形式的非实数值。对于这类不确定型群体决策问题的研究具有重要的理论意义和实际应用价值，因为它符合人类思维具有的不确定性特征，对决策者的思维过程刻画比较符合实际状况，因而它描述的决策过程也就更加细致与真实。在不确定型多属性群体决策中，群体决策者面对决策属性时往往使用没有明确偏好信息的区间数作为评价值，首先需要对区间数信息进行集结处理，然后选择最优备选方案或进行方案排序［1］。目前，不确定型多属性群体决策在管理科学、决策理论、系统工程、运筹学等学科研究中都占据十分重要的地位，已经广泛地应用于投资决策、项目评价、方案优选、工厂选址、经济效益综合评价等诸多领域，具有重要的理论价值和应用前景。根据国内外相关文献，把投影模型引入群体决策中用于集成决策者的属性权重获得群体属性权重，并使用Dice模型作为集成决策信息的研究没有报道［2，3］，大多数文献都采用TOPSIS法［4～6］和可能度法［7～20］。本文针对属性权重和决策者权重均为未知的不确定型多属性群体决策问题，利用规范化处理后的属性值，建立各决策者的理想解权重模型并用投影模型集成求得群体属性权重，同时还计算各决策者的权重，进而集成得到群体的综合决策矩阵，并计算各方案与群体理想解的Dice相似度，再根据各方案与群体理想解的Dice相似度值大小对各方案进行优劣排序。最后，通过实例对该算法进行详细验证，结果表明本文提出算法的有效性和实用性。

1 不确定型多属性群体决策模型

1.1 数据规范化

1.2 各决策者的属性权重

1.3 确定决策者的权重

1.4 群体决策的Dice相似度

若方案与群体正理想解的相似度值越大，则对应的方案就越优。因此，以相似度值作为决策标准，相似度值越大则对应的方案就越好，相似度值越小则对应的方案就越差，从而可以确定群体对方案的决策排序。

2 不确定型多属性群体决策的Dice算法

不确定型多属性群体决策的Dice算法，首先分别计算各决策者的理想解权重，再集结成系统属性权重，同时计算各决策者的权重，可以通过系统属性权重和决策者权重集结成群体综合决策矩阵，然后利用群体正理想解作为参照物，计算各方案与群体理想解的Dice相似度，并以Dice相似度值作为排序依据，确定各方案的优劣排序。因此，其详细步骤如下：

步骤1对不确定型多属性群决策，决策者El给出决策矩阵并按照式（3）和（4）对决策矩阵进行规范化处理，得到决策者El的规范化矩阵

步骤2根据式（9）计算属性权重向量W*，并归一化后得到系统属性权重向量W**；

步骤3按式（14）计算决策者El的权重λl（l∈Q）；

步骤4由系统属性权重向量W**和决策者El的权重λl（l∈Q），得到群体综合决策矩阵

步骤5计算备选方案Xi与群体正理想解X*的Dice相似度；

步骤6根据Dice相似度由大到小对方案进行排序，相似度越大则对应的方案就越优。

因此，不确定型多属性群决策的计算流程如图1所示。

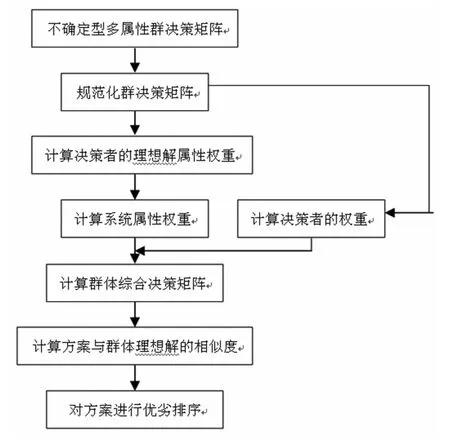
图1 不确定型多属性群决策的Dice算法

3 算例

某投资银行决定对该市3家企业进行投资，由4位专家组成群体考查这3家企业，采用社会效益、环境污染和经济效益等3项指标作为综合评估依据，以便作出重点投资决策，其中社会效益和经济效益为效益型属性指标，而环境污染为成本型属性指标。假设这3家企业的各项指标值均以区间数形式表示，4位专家群体的决策矩阵分别为

（2）根据式（6）计算4位决策者的理想解权重，分别得到：

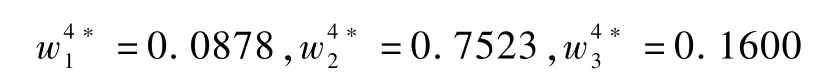
因此，可以得到4组权重组成的向量矩阵：

按照式（7）标准化后，得到：

通过Matlab 6.0软件计算出，式（10）中矩阵STS所对应的最大特征根λmax为0.7212，其对应的特征向量为W**＝（0.3721，0.4929，0.1350）T。

（3）根据式（13），求出4位决策者的系统属性权重为：

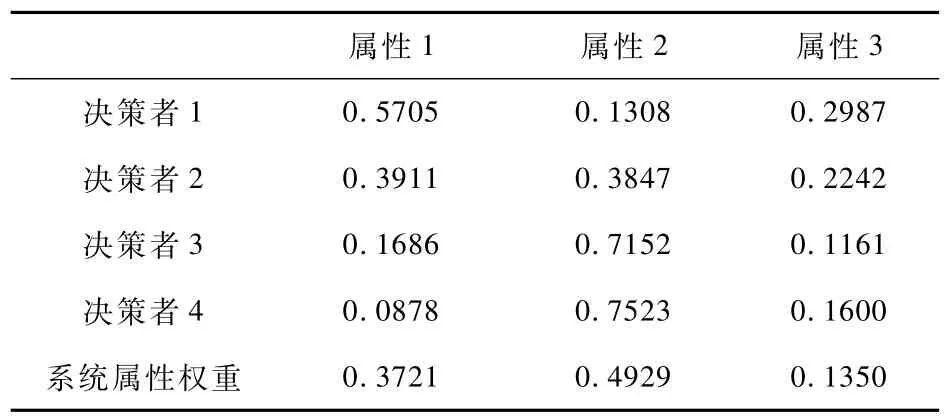
表1 各决策者的属性权重与系统属性权重

（4）计算各决策者权重：

根据定义6，求出群体正、负理想解分别为：

计算各决策者权重，如表2所示：

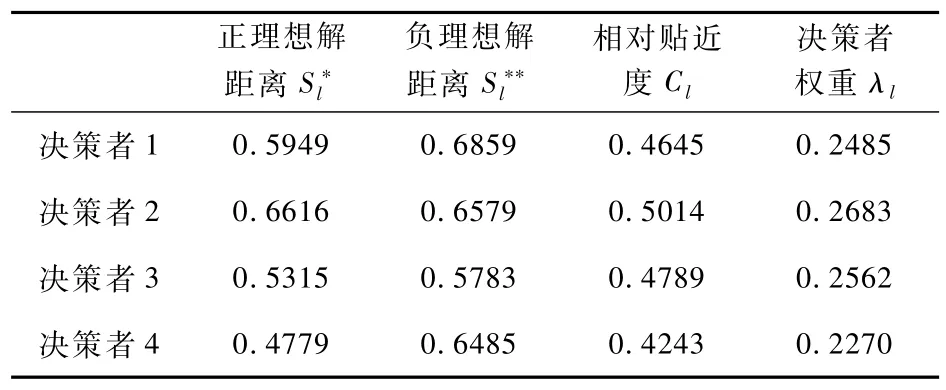
表2 各决策者权重

（5）计算群体综合决策矩阵为：

（6）根据式（18）计算各方案的Dice相似度分别为：D（X*，X1）＝0.9830，D（X*，X2）＝0.9952，D（X*，X3）＝0.9883。

（7）根据Dice相似度的大小对方案优劣排序为：方案2≻方案3≻方案1。

4 结束语

本文针对属性权重和决策者权重均为未知的不确定型多属性群决策，首先建立各决策者的理想解权重优化模型，然后采用投影模型对各决策者的属性权重进行非线性集成，进而得到系统属性权重，同时利用投影模型计算决策者权重，并进一步得到群体综合决策矩阵，由群体综合决策矩阵计算出各方案与群体理想解的Dice相似度，然后根据Dice相似度大小确定各方案的优劣排序。目前，针对区间数不确定型多属性群决策问题，大多数文献采用TOPSIS法和可能度法，而本文的方法更简洁与实用。最后，利用实例验证了整个决策的详细计算过程。本文的计算过程概念简单、思路清晰、操作方便，对处理复杂的不确定型多属性群体决策具有很强的实效性和可操作性。