应用改进混合进化算法求解零空闲置换流水车间调度问题

裴小兵，李依臻

（天津理工大学 管理学院，天津 300384）

0 引言

置换流水车间调度问题（Permutation Flowshop Scheduling Problem，PFSP）是典型的NP难问题，已经成为学术界研究的热点。在该问题的几个不同的评价指标中，最大完工时间最小化是文献中最常用的评价指标［1］，总拖期时间最小化也是常用指标，在现实生产中具有重要的意义。在约束条件方面，零空闲约束已经成为置换流水车间调度问题的重要约束条件，在实际生产过程中，对于节约成本、降低能耗具有重要的研究意义。基于此，本文以总拖期时间最小化为目标来研究零空闲约束条件下的置换流水车间调度问题。

零空闲置换流水车间调度问题（No-idle Permutation Flow-shop Scheduling Problem，NIPFSP）是经典置换流水车年调度问题的扩展。零空闲约束是指在实际生产过程中使用高耗能、贵重机器的情况下，空载运行通常会造成巨大的资源浪费。

目前，国内外对零空闲约束置换流水车间调度问题的研究相对较少。Tasgetiren M F等［2］以总流程时间最小为目标，提出了一种变量迭代贪婪算法求解零空闲置换流水车间调度问题，实例验证结果显示该算法具有较好的求解效果。武磊等［3］以总流经时间和最大完工时间为目标求解NIPFSP问题，提出了和声搜索调度算法，由于采用局部搜索算法，难以保证解的多样性。Shao W 等［4］运用混合节点和边缘直方图的随机样本交叉方式，提出了文化基因算法求解NIPFSP问题，该算法采用随机样本交叉操作，难以保证交叉结果的有效性。刘长平等［5］以完工时间最小化为目标求解零空闲置换流水车间调度问题，提出了离散萤火虫优化算法，并通过典型算例验证了算法的稳定性和高效性。Ying K C等［6］以最小化完工时间为目标，提出了迭代引用贪心算法，首次研究了分布式零空闲置换流水车间调度问题。Sun Z等［7］以总拖期时间最小化为目标，提出了基于分布估计算法和布谷鸟搜索的混合算法求解NIPFSP，该算法虽然取得了较好的求解结果，但分布估计算法的概率矩阵包含信息不足，无法保证知识学习的有效性。Shao W等［8］基于元启发式算法，提出了混合离散教与学算法求解总拖期时间最小化的零空闲置换流水车间调度问题，该算法由三个阶段组成，在离散教学阶段，采用共识置换的思想代替平均个体，并通过标准算例验证了算法的求解效率和算法的有效性。刘翱等［9］针对NIPFSP提出了带有局部搜索的离散烟花算法，虽取得了较好的结果，但采用反转交叉操作重新定义爆炸算子和变异算子的能力相对较弱。Nagano M S等［10］以总拖期时间最小化为目标，提出了两阶段启发式算法求解NIPFSP，该算法采用成组插入的方式，对序列产生较大破坏，但对于优势序列，成组插入具有盲目性，对序列产生较大破坏，不利于增加种群的多样性。Shen J N等［11］为提高搜索效率和种群多样性，将双种群应用于分布估计算法，并以总拖期时间最小为目标求解NIPFSP。Tasgetiren M F等［12］首次提出离散人工蜂群算法求解NIPFSP，该算法参数控制少，具有较强的鲁棒性，但容易陷入局部最优，由于防止该缺陷的最好方法是增加种群多样性，会延长算法计算时间，收敛速度较慢。

近年来，片段或关键块的概念在降低问题复杂度，提高算法求解质量和求解速度方面取得了明显的成效。Chang P C等［13］运用二元变量概率模型，依据概率矩阵并结合轮盘赌法，挖掘优势关键块，提出了基于关键块的进化算法求解PFSP问题。由于具有竞争优势的基因有时不具连续性，Hsu C Y等［14］提出了利用关联规则挖掘不具连续性的基因组合，避免关键块组合方式的单调性而导致种群多样性不足，但该算法完全采用随机方式进行初始化，无法保证初始解的质量。

本文针对NIPFSP的特点提出了一种基于关键块的混合进化算法（Hybrid Evolutionary Algorithm Based on Key Blocks，HEABKB），该算法首先采用NEH（Nawza-Enscore-Ham）启发式产生一个较优的初始解，然后依据关联规则组合连续或不连续的优势关键块，结合优势关键块组合人工染色体。同时，引入双精英进化机制［15代替传统的交叉变异方式，避免相似度较高的染色体之间的无效交叉，增加种群的多样性，加快收敛速度，以获得更优的解。

1 零空闲置换流水车间调度问题模型

NIPFSP问题定义如下：一个工件的集合J＝｛J1，J2，…，Jn｝，需要在m台机器M＝｛M1，M2，…，Mm｝上进行加工。每个工件Jj连续在m台机器上进行加工，每个工件的第i项作业必须在Mi上进行加工，直到加工作业完成。在加工过程没有中断的情况下，工件Jj的加工时间为p（j，i）。设一个加工序列为π＝｛π1，π2，…，πn｝。序列πe（1）＝｛π1｝，序列πe（2）＝｛π1，π2｝，…，序列πe（n）＝π。令F（πe（k），i，i+1）为序列πe（k）完工后，机器i和i+1的完工时间之差。则其数学模型表示如下：

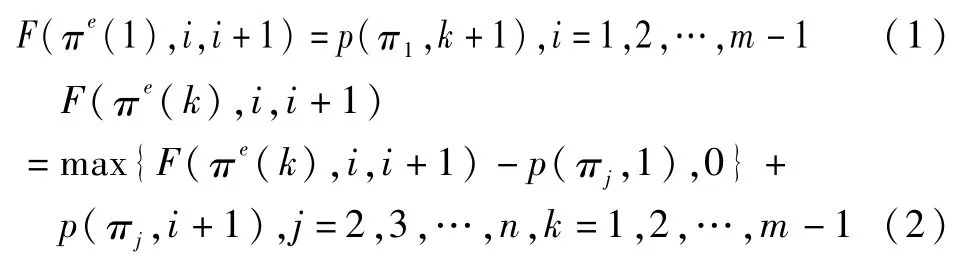
则第n个工件在机器m上的完工时间为：

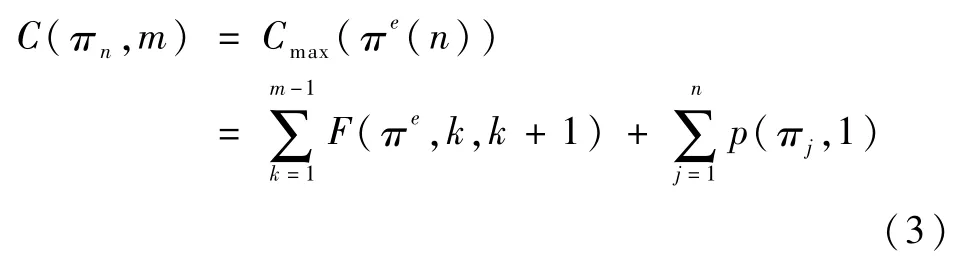
式（3）表示工件πn在最后一台机器m上的完工时间。因此，在最后一台机器m上，工件πj的完工时间为：

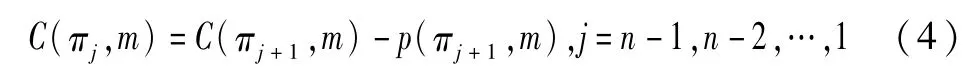
总拖期时间计算公式为：

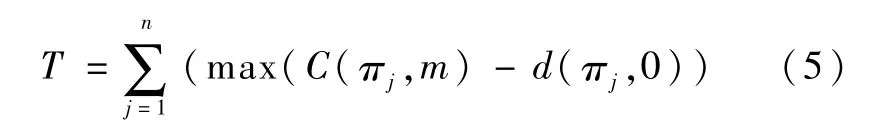
式（1）、式（2）表明了加工过程的零空闲约束。当考虑零空闲约束时，从第二个机器开始必须延迟第一个工件的开始加工时间，保证当一个工件完成时，下一个工件可即刻进行加工。求解NIPFSP的目标值由可行解的总拖期时间T最小来确定。

2 求解NIPFSP的混合进化算法设计

HEABKB算法以遗传算法为框架。考虑到NIPFSP是典型的NP难问题，通过关联规则挖掘关键块，降低问题的复杂度，加快算法的求解效率。由于遗传算法易于陷入局部最优，且传统的交叉变异方式效率较低，本文采用双精英协同进化机制，通过种群分割，将种群分为优势种群与普通种群，对两个种群分别采用不同的进化机制，避免进化过程中的无效交叉，提高算法的进化效率。局部搜索策略，依据关联规则挖掘精英进化子代中的关键块，提取出非关键块；基于染色体的邻域结构，结合NEH算法的思想，对非关键块进行破坏重组，更新子代最优解。

HEABKB算法主要由六部分组成，第一部分运用NEH算法进行种群初始化；第二部分采用关联规则挖掘关键块，通过关键块之间的竞争，保留优势关键块；第三部分组合人工染色体，产生具有较优个体的种群；第四部分，运用双精英进化机制对人工染色体种群进行遗传操作，增加种群的多样性，以获得较优的解，提高算法收敛速度；第五部分，局部搜索策略，进一步提高算法求解质量；第六部分，保留优势种群。各部分具体操作如下。

2.1 种群初始化

初始化种群质量的好坏对于算法后续操作具有重要的影响，好的初始种群可以极大提高算法的搜索效率。NEH算法是最常用的初始化方法之一，其核心是总加工时间最大的工件具有优先权［16］。本文利用NEH算法产生一个具有较好适应度值的解，剩余解以随机方式产生。具体步骤如下：

步骤1计算每个工件在m台机器上的总加工时间：式中，p（j，k）表示工件j在机器k上的加工时间。

步骤2将计算结果dj按降序进行排列。

步骤3从第2步的排序中选择加工时间最大的两个工件，通过计算两个可能序列的拖期时间来找到这两个工件的最佳排序。保持两个工件的相对位置，令j＝3。

步骤4在步骤2降序排列的结果中选择第j个工件，并通过将其放置在上一步骤中找到的部分序列中的所有可能的j个位置来查找最佳序列，不更改已分配作业的相对位置。此步骤中的枚举数为j。

步骤5如果n＝i，则停止操作；否则，令j＝j+1，继续第4步操作。

2.2 基于关联规则的关键块选取

通过基因结构来组合关键块对于降低问题的复杂度、提高算法求解效率具有明显的优势。针对调度问题，本文利用关联规则，分析染色体的结构，通过寻找基因间的相关性，找到优势基因组合形成关键块。

2.2.1 关联规则

关联规则［17］在数据挖掘技术中具有重要的作用，对于提高算法求解效率具有重要意义。本文则引入关联规则来挖掘优势染色体上的优势基因，组成关键块，加快算法的收敛速率。

在表示x→y的关联规则时，主要有两个重要的参照指标，即支持度与信心水平［18］。支持度是指x与y两个数据集同时出现在数据记录里的频率，信心水平是指x与y两个数据集之间的关联强度。另外，还有一个评价指标增益值，它用来判定关联强度，若增益值大于1则为强关联性。

定义如下符号：

N：染色体总数；

ρ（x∪y）：基因集x与基因集y同时出现在合个总体的总次数；

ρ（x）：基因集出现在各个体的总次数；

s（x→y）：基因集x和基因集y之间的关联支持强度；

c（x→y）：基因集x和基因集y之间的关联信心强度；

lift：评价指标增益值，判断基因集x和基因集y之间是否存在强烈的关联度。

计算公式如下：

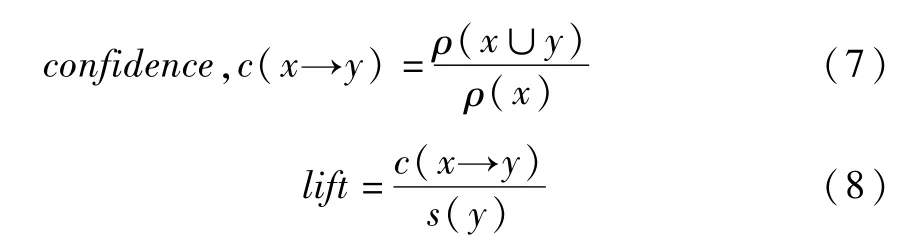
为使关联法则成立且有意义，需设立最小支持度和最小信心水平，当运用关联规则进行挖掘时，超过所设立的阈值，才能认定为有意义的信息。

2.2.2 构建与挖掘区块

关键块是一个具有高度竞争优势的基因结构，对于降低所求问题的复杂度具有显著的效果。本研究通过关联规则构建关键块。挖掘优势的基因结构并组合成关键块，首先将各代群体中的数据依照适应度值的升幂进行排列，并选出前i条染色体，将所选染色体的工件顺序转化为工件加工记录数据集，如图1所示，将染色体的5个工件的解转化为工件加工记录数据集。

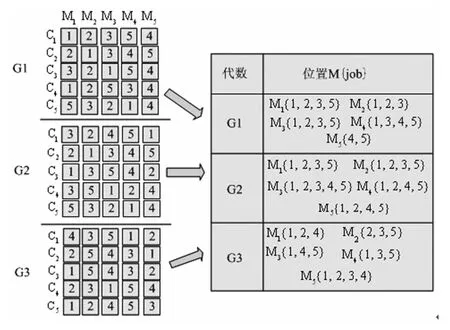
图1 数据编码

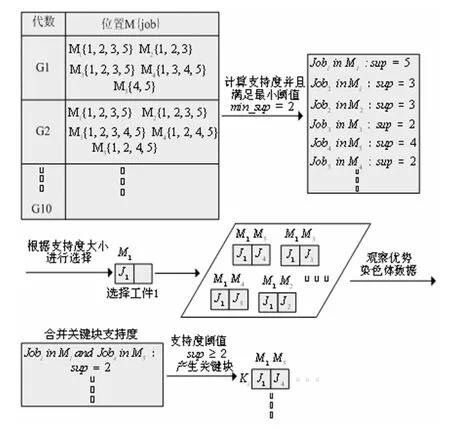
图2 关键块构建过程

在得到工件加工记录数据集后，需设立最小支持度阈值（sup）和关键块的最大长度，根据所得数据找出大于sup的工件与所对应的机器。关键块的产生步骤如下：

步骤1从所得工件加工记录数据集中找出大于所设阈值的部分基因并放入频繁项目集H中；

步骤2把频繁项目集联结为基因关键块组合的候选项目集L；

步骤3在候选项目集L中找出大于阈值的基因关键块，并将其作为新的频繁项目集H′，直到穷尽所有大于阈值的基因关键块。

图2给出上述步骤关键块挖掘构建的过程。

2.2.3 关键块筛选

本研究运用关联规则数据分析方法产生关键块，将单个基因作为候选项目集向外延伸。将关键块的长度设置为2，对关键块暂存器中的关键块的工件与机器进行对比，若关键块之间出现重复的工件或涵盖的机器出现重复，具有重复的关键块将对其增益值进行比较［19］，如果增益值大于1且数值较大，则说明该关键块组合有更强的关联度并进行保留，不满足规则的关键块则被删除。区块筛选过程如图3所示，通过竞争后保留下来的关键块将进一步组合人工染色体。

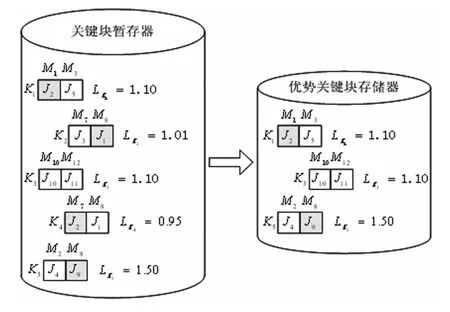
图3 关键块筛选

2.3 构建人工染色体种群

本研究期望获得具有高度竞争优势的人工染色体［20］，以此来提高算法的求解质量和收敛速度。本研究在构建人工染色体的过程中，先将关键块数据中的所有优势块复制到人工染色体上，人工染色体中尚未放入工件的空位置，将由非关键块的工件以随机的方式放入人工染色体中，直到产生完整的人工染色体。步骤如下所示：首先，将挖掘和筛选后的优势关键块直接复制到人工染色体的相应位置，把关键块中相对应的工件和机器位置直接放入人工染色体的相应位置；然后，挑选出尚未分配的工件集合，以随机方式从中选择工件将其放入未安排的机器位置，直到人工染色体完成组合。

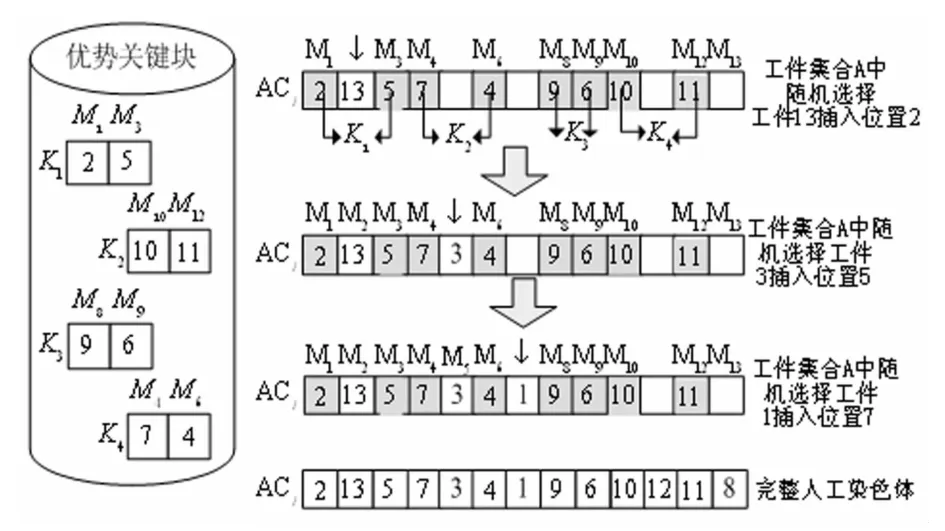
图4 人工染色体组合机制

2.4 双精英协同进化

2.4.1 协作变异机制

协同进化是改善进化算法性能的有效途径［21］，它将个体拆分成多个子集，每个子集对应一类决策，子集独立进化，将进化后的子集组合成完整的解，对完整的解进行评价，实现子集种群的选择。为了避免算法陷入局部最优解，研究过程采用协作交叉变异操作机制，选择两个相异且具有高适应度的个体作为进化的中心，组合各自的进化子种群［14］。为避免相似个体间的无效交叉，将水平集概念应用于该操作机制，进行种群分割，通过协作交叉机制提高算法的搜索能力。

定义1二进制编码空间为｛0，1｝L，种群规模为n，种群的集合AC＝｛AC1，AC2，…，ACn｝，个体ACi和ACj之间的差异度为ACsj），i，j＝1，2，…，n，式中和ACsj分别表示第i和第j个个体上第s位的值，若个体上的每一位都相异，则差异度DD（i，j）＝1；若每一位都相同，则差异度DD（i，j）＝0。

定义2设群体所包含的个体染色体集合AC＝｛AC1，AC2，…，ACn｝，染色体种群规模为n，适应度函数为，令集合称为T关于AC的水平集。

定义3（种群分割）将所得优势个体染色体的集合AC，按照适应度函数的升序进行排列，根据定义1水平集的概念，记下大于等于的最小个体位置，将整个染色体集合分割成两部分，大于等于的记为UAC，小于记为LAC。

利用定义3种群分割的思想，将种群分割为两部分，对这两部分分别采用不同的进化策略。种群人工染色体的组合方式如图4所示。分割可以充分利用种群信息，有效提高算法方向性和适应性。对LAC采用协作交叉机制，本文采用两种交叉操作的协作机制，即单点交叉和翻转交叉。设置差异度值μ＝0.75，当DD（i，j）＞μ时，采用翻转交叉机制产生新个体；DD（i，j）≤μ时，采用单点交叉机制产生新个体。如图5所示。

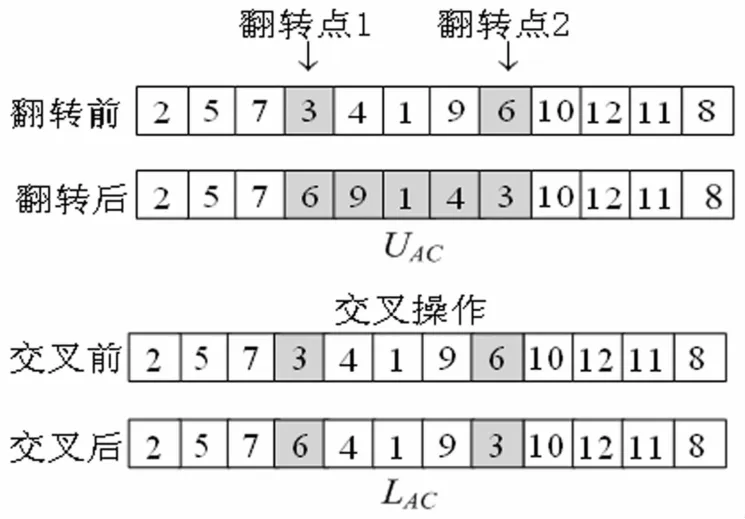
图5 协作变异操作示意图

2.4.2 双精英进化机制

精英个体对种群进化具有重要的作用，本文采用双精英进化策略，以加快算法的全局收敛，将精英染色体作为进化的核心，运用精英染色体推动进化过程，引导其他染色体朝着好的方向进化。在形成的人工染色体集合中，两个适应度最优的精英个体EA和EB分别作为协同进化的中心，共同完成算法的进化过程。

以EA作为进化的中心，提高算法的收敛速度，EA代表每一代人工染色体中适应度值最优的个体。首先，通过种群分割将人工染色体集合分割成两部分：优势种群（LAC）和普通种群（UAC）。根据种群属性，分别采用不同的交叉策略，避免因种群个体过于相似而导致的无效交叉，以提高算法进化效率。EA进化模型如图6所示。

图6 精英A进化图

以EB作为进化中心，避免算法由于选择压力出现过早收敛，在以EB为中心的进化过程中，采用翻转交叉机制，同时，结合个体差异度的概念，避免过度依赖适应度值的大小使算法陷入局部最优，降低种群的多样性。代数增加，种群多样性会降低，此时引入初始种群，以维持种群的多样性。子种群进化模型如图7所示。

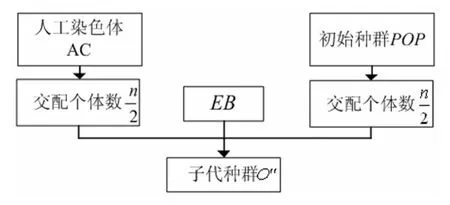
图7 精英B进化图

2.5 局部搜索策略

产生的子代通过执行局部搜索，进一步提高求解质量，加快收敛速度。NIPFSP的解是工件自然数序列的排序，其常用邻域类型主要有插入邻域和交换邻域结构。插入邻域结构是将当前解中的一个工件剔除，并将它依次插入到解中的其他位置。交换邻域结构是指选定一个工件进行交换，对所有工件都执行这样的操作，然后选取最好的解作为该邻域的最优解。

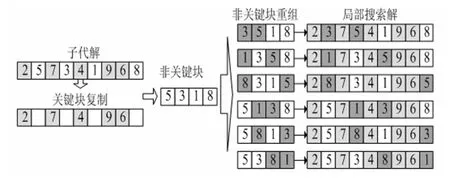
图8 局部搜索方法

首先，根据关联规则，挖掘子代中的优势关键块，保持子代中优势关键块的位置不变。基于交换邻域结构，结合NEH算法的思想，对每一条子代解非关键块实施破坏和重组构造，互换非关键块上的两个工件之间的位置，直到所有非关键块均完成一次交换重组，将重组后的非关键块依序插入到关键块剩余基因位置，得到局部搜索解，如图8所示。计算局部搜索解的适应度函数值，并与子代解的适应度函数值进行比较，如果局部搜索解优于子代解，则替换子代解，否则保留子代解。

2.6 优势种群保留

通过种群重组生成新的子种群，子种群与此世代的原始种群进行比较筛选，结合二元竞赛法［22］，选择新的种群进行下一世代的演化。符号表示及步骤如下所示：

AC：代表人工染色体种群，AC＝｛AC1，AC2，…，ACn｝；

O：代表精英进化染色体种群，O＝｛O1，O2，…，On｝。

步骤1将人工染色体种群AC及所产生的精英进化染色体种群O混合放入选择池中；

步骤2从选择池中随机选择两条解，将适应度函数值高的解放入新的母体中，另一条则放回选择池继续筛选；

步骤3重复步骤2，直到得到新的种群与原始种群同等大小为止。

假设染色体长度为5，种群筛选过程如图9所示。

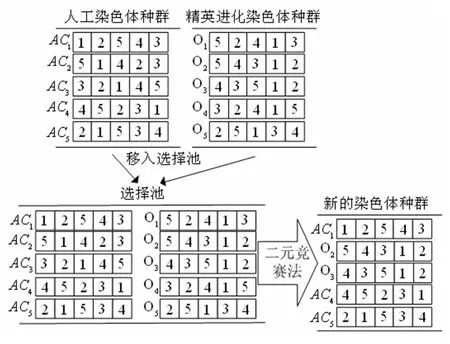
图9 优势种群保留

3 仿真实验

3.1 参数设置

本文所提出的算法程序采用C++语言进行编写，在Windows10（64位）操作系统，Intel（R）Core（TM）i5-4200M CPU@2.50GHz 2.50GHz，内存为8G的环境下运行。本文算例采用Taillard［23］提出的标准例题检验算法的有效性，并与其他算法进行对比。本研究的部分参数通过实验进行确定，进化算法的种群规模设置为NP＝100，交叉概率和变异概率分别为0.75和0.09。计算相对于NEH算法所得结果的平均相对偏差，每个问题的案例运行5次，将每次运行的结果与NEH算法求解NIPFS问题所得的结果进行比较。

记录五次运行中的最小值、最大值、平均值和标准偏差相对于NEH所得解的平均相对百分比偏差，公式如下：

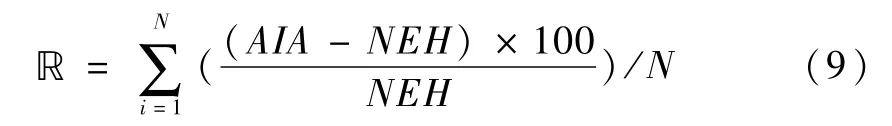
其中，AIA、NEH和N分别表示每次运行某个启发式算法所产生的目标函数值、NEH初始化所产生的值和运行次数。如果ℝ 小于0，则表示算法比NEH所得解更好；ℝ 的值越小，表明解的结果越好。为便于获得本文算法、BEDA算法［21］和DABC算法［12］的收敛图，并进行比较，将终止时间设置为t＝0.1×n秒。达到最大运行时间t＝0.1×n秒时，得到基于交货期紧度因子的三个水平的最优解。在研究拖期准则问题时，交货期的确定是一个主要问题。本文采用文献［24］提出的TWK规则计算交货期。工件j的交货期公式如下所示：

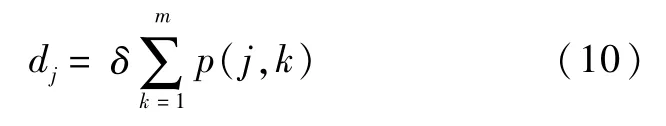
3.2 运算结果分析与比较

为验证本文提出的HEABKB算法的求解性能，分别与文献［11］中的BEDA算法和文献［12］中的DABC算法进行比较，对每一个算例独立运行五次，分别记录五次运行中的最小值（最优值）、平均值、最大值（最差值）和标准偏差。对于交货期宽裕度的每种情况，运行结果按n和m的组合分组。比较的结果在表1到表3中列出，进化曲线如图10到图12所示。

表1 运行结果（δ=1）

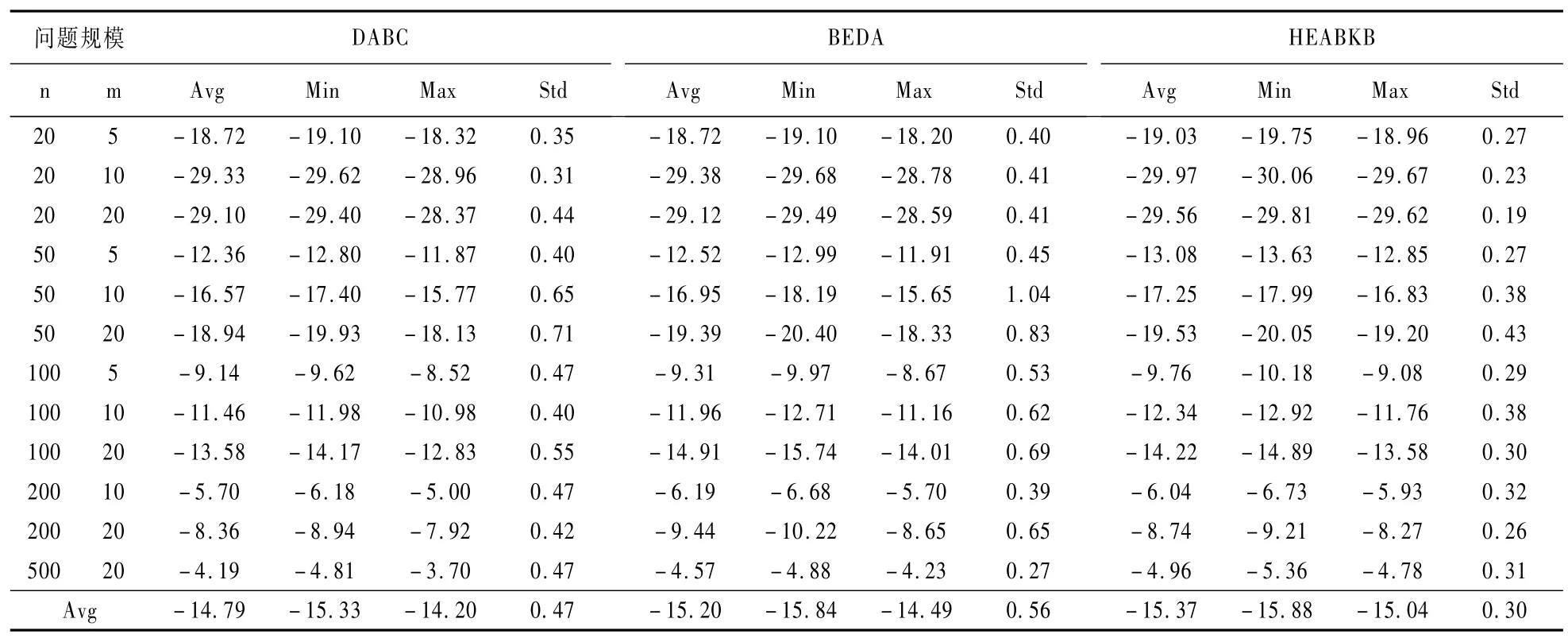
表2 运行结果（δ=2）

表3 运行结果（δ=3）

由表1到表3的结果可知，在求解NIPFSP问题时，针对三个不同的交货期宽裕度系数δ，本文提出的HEABKB算法优于DABC和BEDA算法。当达到终止准则，算法运行所得结果的最小值、平均值和最大值可明显看出HEABKB算法可以获得更优的解。图10至图12表示交货期宽裕度系数分别为1、2、3时，三种算法的平均相对偏差收敛曲线图，进一步表明HEABKB算法收敛速度更快，求解效率更高，能够得到更好质量的解。

图10 算法仿真收敛图（δ＝1）

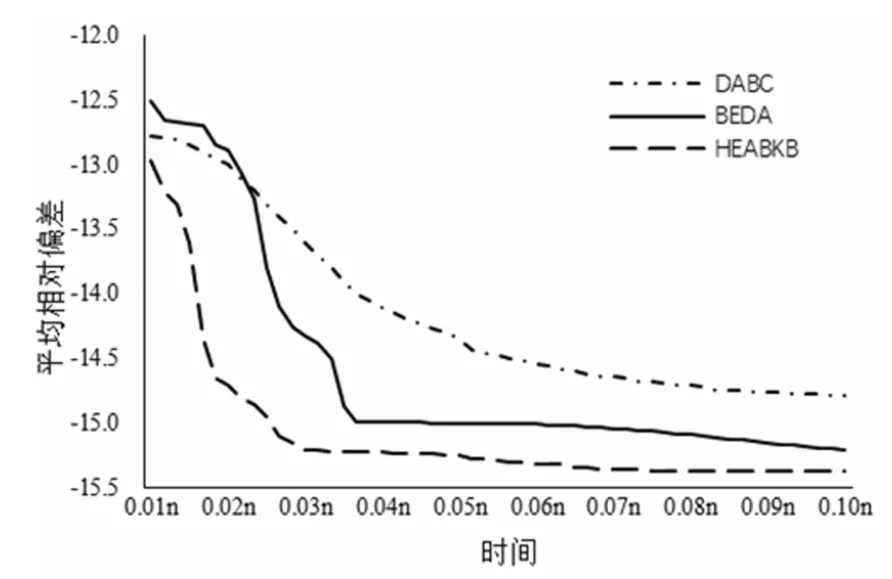
图11 算法仿真收敛图（δ＝2）

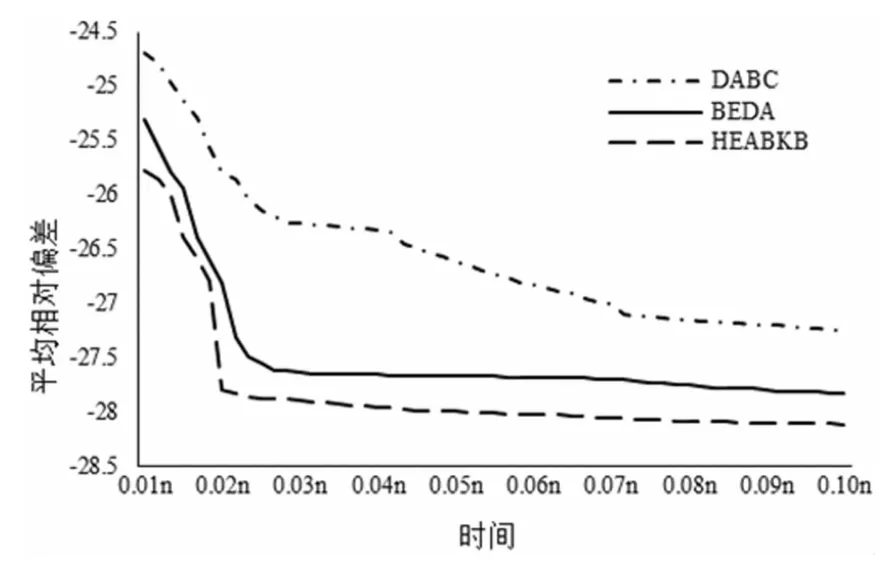
图12 算法仿真收敛图（δ＝3）

为进一步分析数据，运行HEABKB算法，对每个算例计算20次，通过t检验来表示HEABKB算法相对于DABC和BEDA算法所得结果在统计学上的显著性。统计检验结果如表4所示。

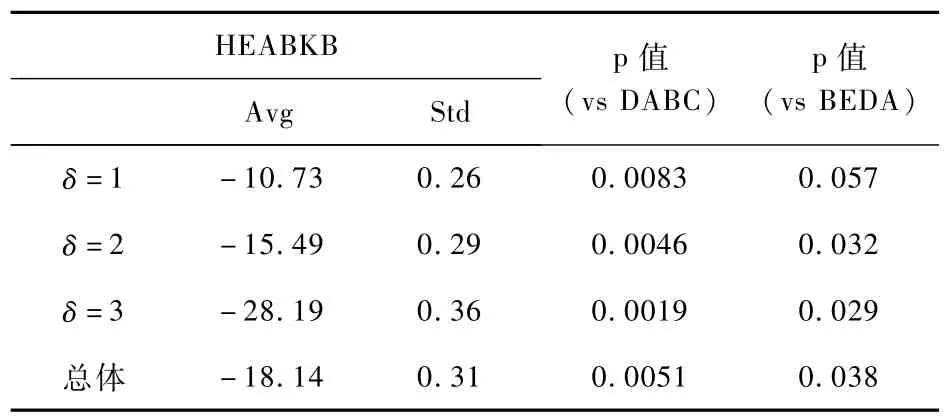
表4 统计检验结果

t检验统计结果显示，HEABKB算法与DABC算法相比，三种交货期宽裕度系数情况下的p值均远小于0.05。对于所有的案例，在置信水平为0.95的情况下，HEABKB算法与DABC算法的运行结果具有统计显著性。HEABKB算法与BEDA算法相比，交货期宽裕度系数为2和3时，t检验的p值分别为0.03和0.02，表明置信水平为0.95时，两种算法的结果偏差具有显著性。当交货期宽裕度系数为1时，p值为0.57，但是考虑所有案例的平均值，p值的平均值为0.03＜0.05，表明在置信水平为0.95的情况下，HEABKB算法运行结果仍然比BEDA算法运行结果具有更优的显著性。以上统计检验结果表明，在求解NIPFSP时，HEABKB算法求解效果更好。该算法的优越性主要表现在两个方面：（1）运用关联规则挖掘关键块，提高了算法的求解效率和解的质量；（2）使用双精英进化策略，增加了解的多样性，避免进化算法的无效交叉，具有更优的全局搜索能力。

4 结束语

本文提出一种基于关键块的混合进化算法（HEABKB）。算法采用NEH和随机方式产生初始种群，并运用关联规则数据挖掘机制，从优势染色体上找出优势基因，组成优势关键块，借助优势关键块进行基因重组，降低求解问题的复杂度，加快算法运行效率。引入双精英进化操作，采用种群分割机制和差异度的概念，避免算法进化过程中的无效交叉和变异，提高种群的多样性和求解质量，产生更具优势的子代种群。局部搜索策略，依据关联规则挖掘精英进化子代中的关键块，提取出非关键块；基于染色体的邻域结构，结合NEH 算法的思想，对非关键块进行破坏重组，更新子代最优解。数据测试结果表明，本文所提算法具有较快的收敛速率，求解效果更好，能够得到更高质量的解。本文算法仅针对单目标问题进行求解，为进一步提高算法的适用性，今后将尝试研究具有多目标的组合优化问题。