考虑有限缓存区的Job Shop加工与搬运集成调度
2021-01-07张维存左天帅张博涵
张维存,左天帅,张博涵
(河北工业大学 经济管理学院,天津 300401)
0 引言
在Job Shop环境下,搬运设备的调度和缓存区容量的设置是影响车间调度优化方案的两个重要因素,将搬运设备和有限缓存区在Job Shop调度问题中集成考虑可以减少生产总成本,缩短产品生产周期,提高资源利用率。因此,如何将两方面同时考虑,将成为本文研究的重点。
近年来,国内外很多学习者在两方面分别做了大量研究。在仅考虑搬运设备的情况下,Egbelu[1]等首次提出了在Job Shop环境下,搬运设备调度的一些启发式规则。Hurink[2]等将单搬运设备调度问题看作具有时间窗的旅行推销员问题,通过禁忌搜索算法解决了 Job Shop排产问题。之后,Hurink[3]等又针对单搬运设备,同时考虑了工件运输时间和空载时间,提出了基于邻域结构的局部搜索算法。何之洲[4]等同样仅针对带单搬运设备的Job Shop调度问题,提出了一种并行禁忌搜索算法,其优点在于调度任务中包括了加工工序的排序和搬运工序的指派。不同于前人,Deroussi[5]等提出了基于搬运设备而非加工设备的解决方案,虽有创新但针对对象仍局限于单搬运设备。
区别于单搬运设备,多个搬运设备的Job Shop问题则不仅需要为各加工工序指派加工设备,同时还需指派搬运设备。如:Driss[6]等首先应用基于邻域搜索的遗传算法进行搜索,其次使用禁忌搜索算法进行工序排序。Lacomme[7]等采用析取图求解多搬运设备的Job Shop问题。Zheng[8]等提出了针对同时调度加工设备和搬运设备的混合整数线性规划模型,该模型由加工设备调度和搬运设备调度子问题组成,采用禁忌搜索算法求解近似最优解。Umar[9]等提出使用模糊专家系统控制遗传算子的混合遗传算法求解加工和搬运调度问题。此外,孔继利[10]等研究了加工与搬运时间、搬运车辆调度和工件移动方式决策等问题,Bekkar[11]等、Karimi[12]等考虑了加工设备间的搬运时间,采用迭代插入操作精确的解决工序排序问题。也有学者综合考虑了多个方面的内容,如:搬运设备和搬运时间[13]、加工与搬运集成调度[14]。以上研究都是在Job Shop调度问题基础上考虑了搬运设备。将搬运设备引入生产系统中,提高生产效率的同时,也产生了更多的瓶颈资源。
另一方面,在Job Shop调度问题中,仅考虑有限缓存区的研究也有很多。如:Rer M[15]等研究了在运输约束和加工设备前后存在缓存区的条件下Job Shop调度问题,Escamilla[16]研究了在非瓶颈区的加工设备存在有限缓存区的Job Shop调度问题,Zhang[17]研究了加工设备可能存在的输入/输出有限缓存区的Job Shop调度问题。除此之外,也有学者对缓存区容量优化问题进行了研究。如:王政球[18]等研究了基于生产调度方案下的缓存区容量优化问题。曹振新[19]等研究了缓存区容量参数,搬运设备数量等性能指标。吕洁[20]等考虑面向多个加工任务同时进行加工时瓶颈资源问题,以减少生产波动对瓶颈资源的影响来针对缓冲区容量问题进行研究,以最优缓冲区容量为目标建立目标函数模型。陈冠中[21]等对智能制造系统中的缓存区最大容量进行配置优化。郭丽[22]等提出了在工件排序方案既定情况下,所优化的目标值与缓存区容量增长不成正比。任晓莉[23]等在考虑调度总时间的同时将库存容量目标进行优化。
综上,国内外学者既对考虑单搬运设备和多搬运设备的Job Shop调度问题进行了深入研究,又对Job Shop制造环境下,缓存区容量优化配置问题进行了广泛研究。然而,作业车间环境下同时考虑搬运设备和有限缓存区的作业排序优化问题却未得到充分研究。该问题的研究,可以同时提高缓存区、搬运设备以及加工设备的资源利用效率,使各类资源进行更好的匹配。此外,由于搬运设备数量和缓存区容量影响着调度方案的效率及可行性,该问题较相应的JSP更具复杂性,所需要搜索的解空间更大。为了解决在缓存容量受限的情况下,加工设备和搬运设备的作业排序问题,本文以最小化最大完工时间为优化目标,设计了一种带启发式信息的具有角色互换机制的人工蜂群算法(G-ABC),求解有限缓存区下Job Shop加工与搬运集成调度问题。
1 考虑有限缓存区的Job Shop加工与搬运集成调度问题的数学模型
1.1 问题描述
带有限缓存区的Job Shop加工与搬运集成调度问题可描述为:n个工件{J1,J2,…,Jn}在m台加工设备M∈{M1,M2,…,Mm}上加工,调度开始前所有工件均在装载区M0处,每台加工设备Mb(b∈[1,m])都有一个输入缓存区IBb(b∈[1,m])和一个输出缓存区OBb(b∈[1,m]),且所有输入/输出缓存区容量均为K。每个工件Ji包括ni道工序Oij(i∈[1,n],j∈[1,ni]),每道工序Oij仅对应一台加工设备Mb。工序Oij作为加工任务,在加工前需由1台搬运设备Hc(c∈[1,h])将工件Ji从上工序Oi(j-1)对应的加工设备Mb′的输出缓存区OBb′搬运到加工设备Mb的输入缓存区IBb中,工序Oij加工完成后工件Ji进入到加工设备Mb的输出缓存区OBb中,等待下次搬运和加工。因此,考虑搬运环节后,工序Oij既是加工任务也是搬运任务。当所有工件{J1,J2,…,Jn}都加工完成且被搬运到卸载区Mm+1时,调度过程结束。调度目标是求出最大完工时间Cmax最小的调度方案。
假设条件:(1)同一时刻一台加工设备只能加工一个工件,每个工件在某一时刻只能在一台加工设备上加工,且操作不可中断;(2)同一时刻一台搬运设备只能搬运一个工件,每个工件在某一时刻只能由一台搬运设备搬运,且搬运不可中断;(3)同一工件工序之间有先后约束,不同工件工序之间没有先后约束,且不同工件具有相同的优先级;(4)零时刻,所有工件放在装载区M0,所有加工/搬运设备可用;(5)不考虑搬运设备的装卸时间和工件在加工设备上的切换时间;(6)所有工件的搬运时间只与加工设备间距离有关。
1.2 数学模型

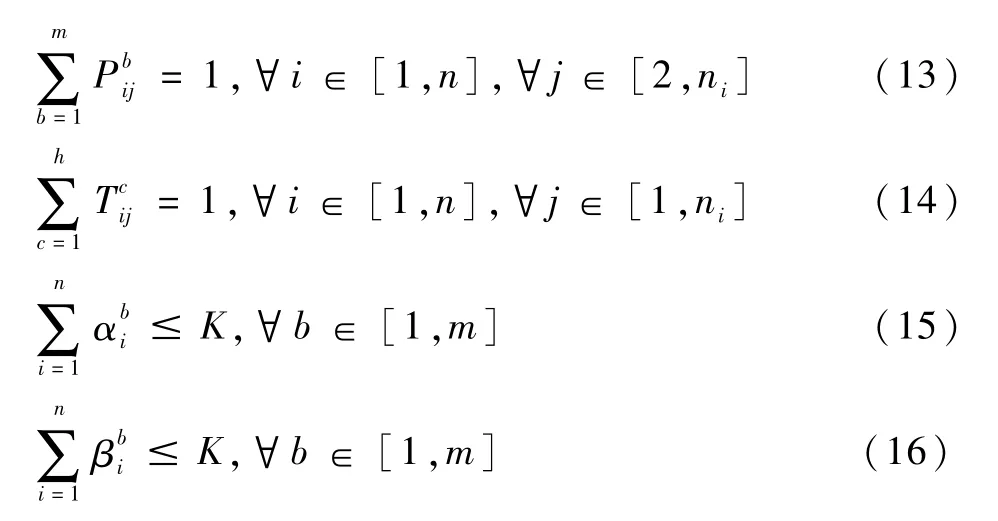
(1)表示优化目标为最大完工时间最小化。(2)表示最小化最大完工时间大于等于各工件尾工序搬运到卸载区时的结束时间。(3)表示工件搬运之后需进入加工设备的输入缓存区,且不允许工件在搬运设备上等待。(4)表示工件进入加工设备的输入缓存区之后才能加工。(5)表示工件加工完成后需进入加工设备的输出缓存区。(6)表示工件进入加工设备的输出缓存区之后才可搬运。(7)表示一个加工设备一次只能加工一个工件。(8)表示一个搬运设备一次只能搬运一个工件。(9)和(10)分别表示同一加工设备上的两个工序之间满足先后顺序关系。(11)和(12)分别表示由同一搬运设备完成的两个工序之间满足先后顺序关系。(13)表示一个工件一次只能分配到一台加工设备加工。(14)表示一个工件一次只能由一台搬运设备搬运。(15)和(16)分别表示输入/输出缓存区内存在的工件数量不可以超过最大容量。
2 改进人工蜂群算法及启发式信息设计
2.1 算法改进设计
标准人工蜂群算法将蜜源位置作为可行解,跟随蜂在引领蜂附近进行局部搜索,侦察蜂可以跳出局部最优进行全局搜索,因此,标准人工蜂群算法在求解问题时存在两个问题:(1)引领蜂与跟随蜂之间如何更加高效的进行位置共享及种群更新;(2)人工蜂群算法在求解问题时容易陷入局部最优解,如何跳出局部最优解,更加充分有效地搜索解空间中的可行解。
由于标准人工蜂群算法的不足,本文既要改进引领蜂与跟随蜂的协作方式,同时也要改进跟随蜂的局部寻优方式,使其随优化问题的寻优状态自适应调整寻优方向。改进思路:首先,由于引领蜂侧重全局搜索,跟随蜂侧重局部搜索,故令两者根据寻优状态可互换角色,以便充分且精细地搜索解空间;其次,以引领蜂位置为中心跟随蜂进行局部搜索,且搜索结果作为引领蜂寻优(觅食)的依据,指引其更好地全局搜索;最后,跟随蜂应根据优化问题的寻优状态,既能高效地局部搜索,又能照顾到更大范围,跳出局部最优。
本文问题不同于传统的JSP,其特殊性在于工序Oij既是加工任务又是搬运任务,且在此调度过程中还需考虑是否超出输入/出缓存区的容量;其复杂性在于不仅需要对加工任务排序,还需为搬运任务分配搬运设备后再对搬运任务排序。基于此问题的特殊性和复杂性,算法的设计思路如图1所示,具体体现为如下四点:(1)算法采用基于工序的编码方式(详见2.2小节)。(2)基于工序的解码状态,设计了工序作为加工任务或搬运任务被选为可解码对象的启发式信息(详见2.3小节)。(3)在解空间中,引领蜂对全局解空间广泛搜索,跟随蜂以其引领蜂位置为中心对局部解空间精细搜索。每只引领蜂和跟随蜂的位置信息都是一个调度方案,调度方案的解码过程详见2.4小节。(4)引领蜂和跟随蜂可根据寻优的具体情况,判断引领蜂位置是否更新以及角色是否转换,以便于自适应调整寻优方向,直到引领蜂数量为1时,寻优过程结束,输出最优调度方案,算法的详细改进步骤见2.5小节。
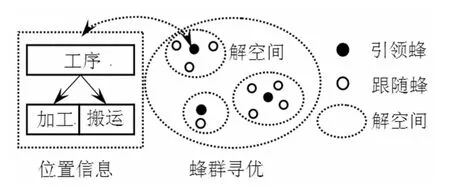
图1 算法设计思路
2.2 编码设计
算法采用基于工序的编码方式,这种编码方式的好处在于,便于算法运行过程中的进化计算,更好的处理离散组合优化问题,进而提高搜索效率。个体中的每个基因位代表工序Oij,包含了工件编号i、工序编号j、加工设备编号b、搬运设备编号c、加工时间、加工优先权值qij、搬运优先权值pij等与工序有关的信息。每一个基因位既包含了加工信息也包含了搬运信息,如图2所示:
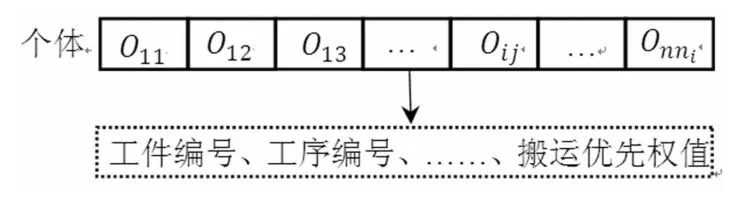
图2 基因编码设计
其中,工件编号i和工序编号j共同作为标识来确定基因位Oij。加工开始时间和搬运开始时间在解码过程中得出,加工优先权值qij和搬运优先权值pij随机赋值,加工优先权值qij作为解码过程中判断工序Oij是否优先加工的依据,同样,搬运优先权值pij作为解码过程中判断工序Oij是否优先搬运的依据。同时,加工优先权值qij和搬运优先权值pij也是蜂群操作的对象,个体通过进化获得新的加工、搬运优先权值后再次进入解码过程。
2.3 启发式信息设计
为提高算法运行效率,并使最大完工时间最小化,在解码过程中设计了工序Oij进入输入缓存区时间、加工优先权值qij、工序Oij进入输出缓存区时间、搬运优先权值pij作为可参照的局部启发式信息。
(1)工序Oij作为加工任务被选为解码对象的依据是,首先按照公式(17)选择进入输入缓存区IBb时间最早的工序,在此基础上按公式(18)选择加工优先权值qij最小的工序。
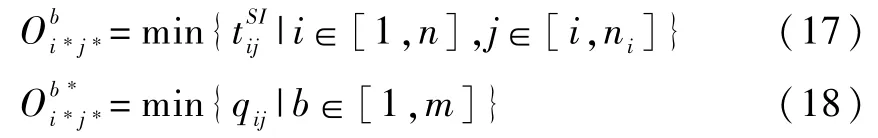
(2)工序Oij作为搬运任务被选为解码对象的依据是,首先按照公式(19)选择进入输出缓存区OBb时间最早的工序,在此基础上按公式(20)选择搬运优先权值pij最小的工序。
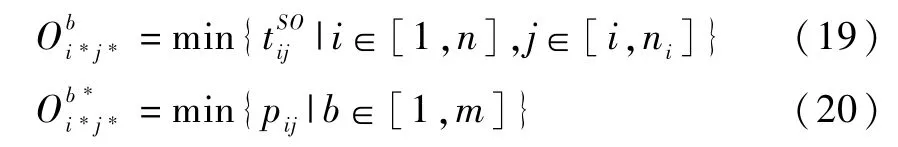
2.4 解码过程
解码过程依据工序的加工和搬运约束条件、加工优先权值qij、搬运优先权值pij,在满足资源约束的条件下,逐步安排各工件工序Oij加工和搬运的先后次序,依次得到工序Oij的开始加工时间、开始搬运时间、进入输入缓存区时间、进入输出缓存区时间、结束加工时间、结束搬运时间,最终得到加工时间最小的排序方案。
本文研究的问题考虑了装载区M0和卸载区Mm+1,假设装载区M0和卸载区Mm+1的容量无限大,并将装载区M0对应的虚拟工序Oi1设为所有工件的首工序,将卸载区Mm+1对应的虚拟工序设为所有工件的尾工序。因此,所有工件的首序Oi1不需要加工只需要搬运,尾工序既不需要加工也不需要搬运。零时刻,所有工件的首工序Oi1可搬运,所有搬运设备H和加工设备M可用,且所有搬运设备H位于装载区M0处。
工序Oij作为加工任务被选为解码对象,需要满足四个条件:(1)工序Oij未被加工(2)上工序Oi(j-1)已被解码;(3)工序Oij已放于对应加工设备Mb的输入缓存区IBb中(4)对应的加工设备Mb空闲。满足以上条件的工序Oij构成可解码加工集合Φ。
工序Oij作为搬运任务被选为解码对象,需要满足四个条件:(1)工序Oij已被加工;(2)工序Oij未被搬运;(3)工序Oij已放于对应加工设备Mb的输出缓存区OBb中;(4)下工序Oi(j+1)对应加工设备Mb′的输入缓存区IBb′有空位。满足以上条件的工序Oij和所有工件的首工序构成可解码搬运集合Ω。具体解码步骤如下:
步骤1逐步遍历各个工序Oij,依据上述条件确定可解码加工集合Φ 和可解码搬运集合Ω。判断集合Φ 和Ω是否均为空,若均为空,则转入步骤5;否则,转入步骤2。
步骤2首先,依据启发式信息,分别选出作为加工任务优先解码的工序和作为搬运任务优先解码的工序,再比较工序的加工优先权值qij和工序的搬运优先权值pij,选出两者优先权值中最小的工序Oij作为当下唯一解码对象。若选中加工优先权值qij最小的工序Oij解码,则令Φ=Φ-{Oij},并转入步骤3;若选中搬运优先权值pij最小的工序Oij解码,则令Ω =Ω-{Oij},并转入步骤4。
步骤3将加工任务Oij对应的工件Ji从输入缓存区IBb中取出,令输入缓存区IBb的计数器ub=ub-1,根据公式(21)计算工序Oij的开始加工时间并判断此时ub是否为K-1,若ub=K-1,根据公式(22)更新输入缓存区IBb最早有空位的时间,否则不变。根据公式(23)计算工序Oij的结束加工时间。判断加工设备Mb的输出缓存区OBb是否有空位,若输出缓存区OBb的计数器vb<K,则将工件Ji放入输出缓存区OBb,令输出缓存区OBb的计数器vb=vb+1,根据公式(24)更新工序Oij进入输出缓存区OBb的时间,根据公式(25)更新加工设备Mb的最早可用时间;否则,加工设备Mb被占用,即不变,直到输出缓存区OBb有空位,即vb=K-1时,再根据公式(28)、公式(29)更新根据可解码条件更新可解码搬运集合Ω,转入步骤1。

其中,加工设备Mb的最早可用时间,根据紧前先于工序Oij在加工设备Mb上加工的工序的具体完工情况,选择公式(2.9)或者公式(2.13)计算得出。
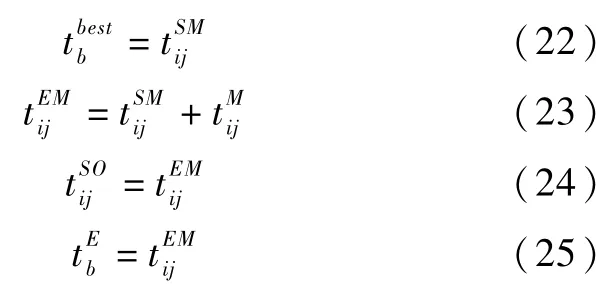
步骤4将搬运任务Oij对应的工件Ji从输出缓存区OBb中取出,输出缓存区OBb的计数器vb=vb-1,依据公式(26)计算可最早到达输出缓存区OBb搬运设备Hc的到达时间并由搬运设备Hc承担此项搬运任务Oij,再根据公式(27)计算工序Oij开始搬运时间。若此时vb≤K且其加工设备Mb上有工件Ji′等待进入输出缓存区OBb,则根据公式(28)和公式(29)更新该工序Oi′j′进入输出缓存区OBb的时间和加工设备Mb的最早可用时间;否则不变。根据公式(30)计算工序Oij结束搬运时间,同时更新下工序Oi(j+1)对应加工设备Mb′输入缓存区IBb′的计数器=,根据公式(31)更新工序Oi(j+1)进入输入缓存区IBb′的时间,根据公式(32)更新搬运设备Hc的最早可用时间及当前位置。根据可解码条件更新可解码加工集合Φ,转入步骤1。
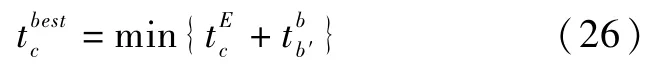
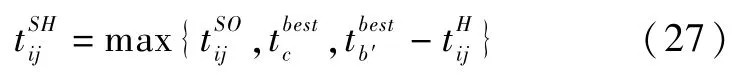
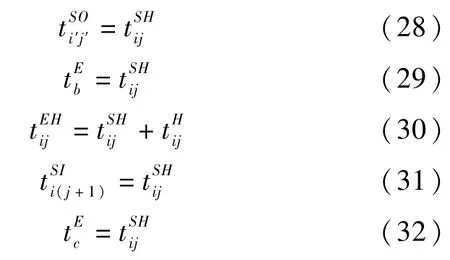
步骤5若集合Φ 和Ω均为空,表示所有工序Oij均已解码,即解码过程结束,根据公式(1)和(2)计算最小完工时间,否则,转入步骤1。
2.5 算法步骤
算法运行前,只需要设定唯一的参数种群规模N,并令引领蜂规模Ne和跟随蜂规模Nu均为N/2。之后进入以下过程:
步骤2初始化蜂群。采用二维蜂群数组,第一维数组作为种群规模,第二维数组存储工序节点。对每个引领蜂个体中工序Oij的加工优先权值qij、搬运优先权值pij随机赋值。
步骤2对每只引领蜂个体位置进行解码,根据解码结果得出对应的目标函数值fe,并由公式(33)计算出每只引领蜂对应的适应值fite。

步骤3由公式(34)计算每只引领蜂可分配跟随蜂规模的概率pe,进而由公式(35)计算其跟随蜂数量,其中,fite表示每只引领蜂的适应值。

步骤4通过对相应的跟随蜂种群寻优,更新相应的引领蜂适应值。具体过程如下:
步骤4.1选定一只引领蜂xe,将位置信息共享给其跟随蜂,即第e只引领蜂的第u只跟随蜂按照公式(36)在其周围搜索更新位置信息。
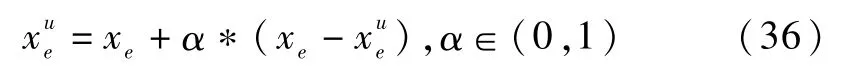
步骤4.2对跟随蜂位置进行解码,得出适应值fitu,若适应值fitu优于引领蜂xe的当前适应值fite,即fitu>fite,则令fite=fitu,引领蜂xe位置得到更新;否则,引领蜂xe适应值不变。
步骤4.3若u=,即引领蜂xe的跟随蜂全部搜索完成,转入步骤4.4;否则,u=u+1,转入步骤4.1。
步骤4.4若e=Ne,即引领蜂全部更新完成,转入步骤5;否则,e=e+1,转入步骤4.1。
步骤5通过引领蜂种群寻优进化,得出最优解,具体过程如下:
步骤5.1Ne只引领蜂的位置以及适应值都得到更新后,将所有引领蜂适应值进行排序,得出最优适应值f′;
步骤5.2根据公式(37)、公式(38),将当前引领蜂位置与最优引领蜂位置进行差分计算,调整当前引领蜂向最优引领蜂位置靠近。其中,pij:当前引领蜂的搬运优先权值:最优引领蜂的搬运优先权值;qij:当前引领蜂的加工优先权值:最优引领蜂的加工优先权值。
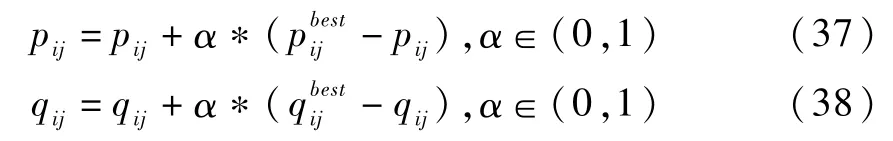
步骤5.3比较最优适应值f′与全局最优适应值f。若f′>f,将适应值最差的引领蜂转化为跟随蜂,即Ne=Ne-1,并令Nu=Nu+1,转入步骤5.4;若f′<f,令f=f′,引领蜂、跟随蜂分别恢复为原来的规模Ne=Nu=N/2,转入步骤2。
步骤5.4若Ne=1,则算法结束,得出最优结果和最优调度方案;否则,转入步骤2。
3 实验分析
3.1 G-ABC算法主要参数实验分析
为提高算法搜索效率,在改进人工蜂群算法中加入启发式信息,形成带启发式信息的具有角色互换的人工蜂群算法(G-ABC)。在G-ABC中,唯一需要确定的只有种群规模。因此,在Windows 10 64操作系统,处理器2.5GHz,内存8GB的计算机上以Visualstudio 2010为实验环境,以EX94测例为例,固定缓存区容量K=1,搬运设备数h=2不变,在不同种群规模N(N=“50”,“100”,“150”,…,1000)下进行求解,每一种群规模均运行20次计算最优均值,得出不同种群规模N下最优均值及最优值的方差,并绘制出随种群规模N变化的最优均值变化图及方差变化图。
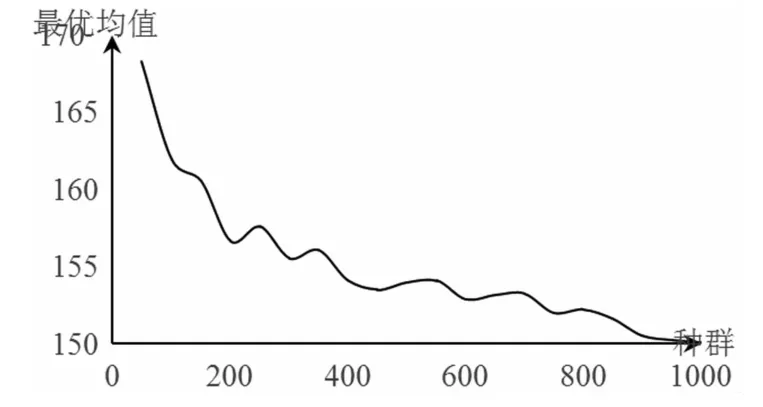
图3 最优均值变化

图4 方差变化过程
从图3可知,种群规模N达到900时,G-ABC求解出的最优均值曲线趋于平缓,说明当种群规模N达到900时,G-ABC算法的寻优能力接近最大极限;从图4可知,种群规模N达到850时,算法每次运行的结果趋于稳定。结合图3、图4可知,种群规模建议设置在900~1000之间较为合理。
3.2 G-ABC算法有效性实验分析
为验证G-ABC算法的寻优能力,引入Bilige等人[24]提出的40个标准EX测例,每个EX测例由工件加工要求(Jobset)和车间布局(layout)两部分组成。例如,测例“EX23”,2表示Jobset 2,3表示layout3。表1中,MAS列表示文献[25]在缓存区容量无限、搬运设备为2的情况下,提出的算法运行结果;GAHA表示文献[26]在缓存区容量无限、搬运设备为2的情况下,提出的算法运行结果。本文考虑了缓存区容量限制条件,所以将G-ABC算法种群规模N设为1000,搬运设备数量h设为2,分别将缓存区容量K设为1,2,3,每种情况均运行20次,取最优值记入A列、B列、C列。GAP1列表示G-ABC算法和文献[25]中MAS的差值比,计算方式:GAP1=(MAS-C)/MAS*100%,若GAP1>0,说明G-ABC优于文献[25]的MAS运行结果。GAP2列表示G-ABC算法和文献[26]中GAHA运行结果的差值比,计算方式:GAP2=(GAHA-C)/GAHA*100%,若GAP2>0,说明G-ABC算法优于文献[26]的GAHA运行结果。
表2中结果的得出方法与表1相同,不同之处在于搬运设备数量h设为3,其中,GAHA3列表示文献[26]中GAHA3的运行结果,GAP3的计算方式:GAP3=(GAHA3-D)/GAHA3*100%,若GAP3>0,说明G-ABC优于文献[26]的GAHA3的运行结果。
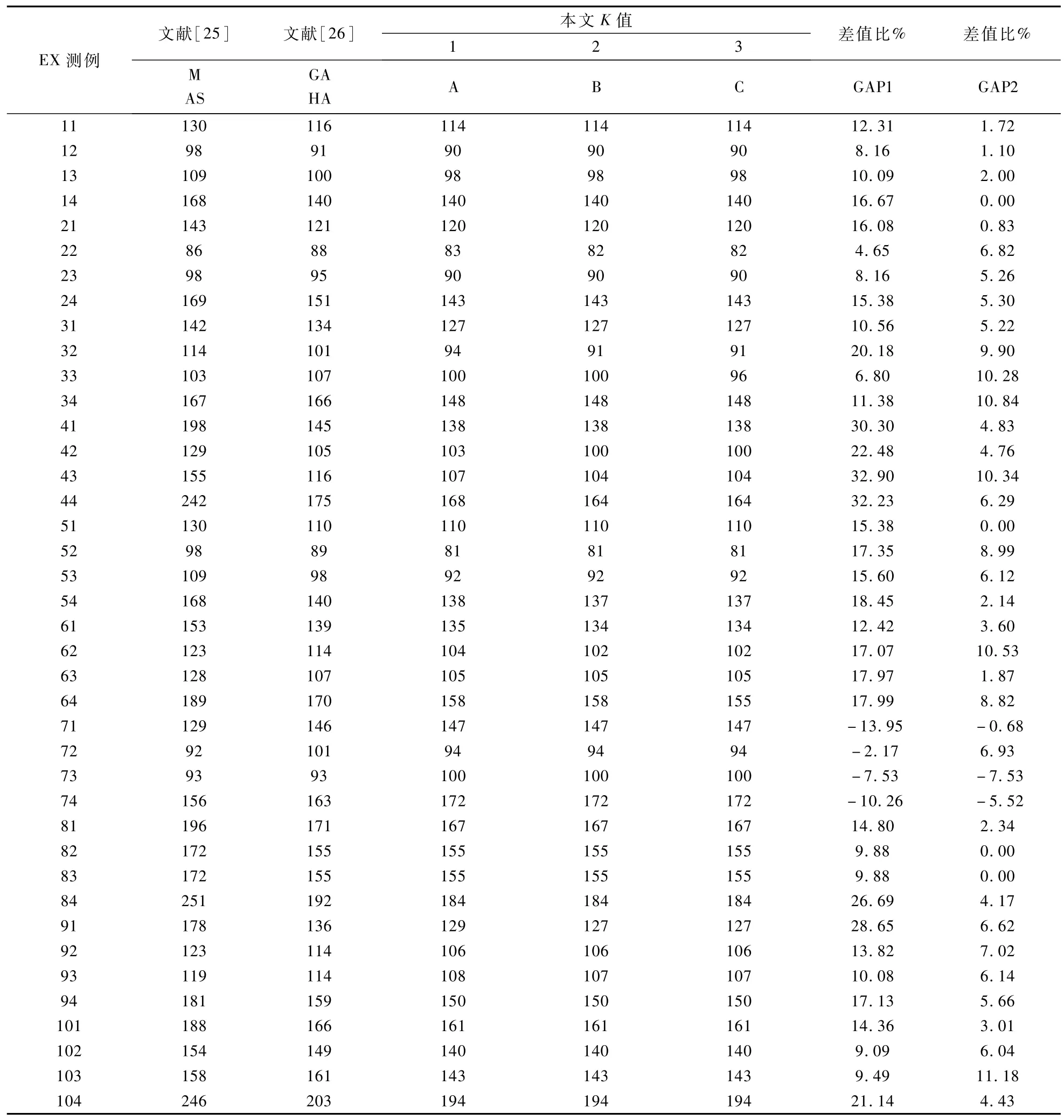
表1 实验及对比结果(h=2)
从表1中的数据可知,G-ABC算法90%的运行结果优于MAS的最优解,最大差值比为32.9%,平均差值比为13.54%,G-ABC算法92.5%的运行结果不差于GAHA 的最优解,最大差值比为11.18%,平均差值比为4.43%,可见G-ABC算法的寻优能力更强,优于MAS和GAHA的寻优能力。
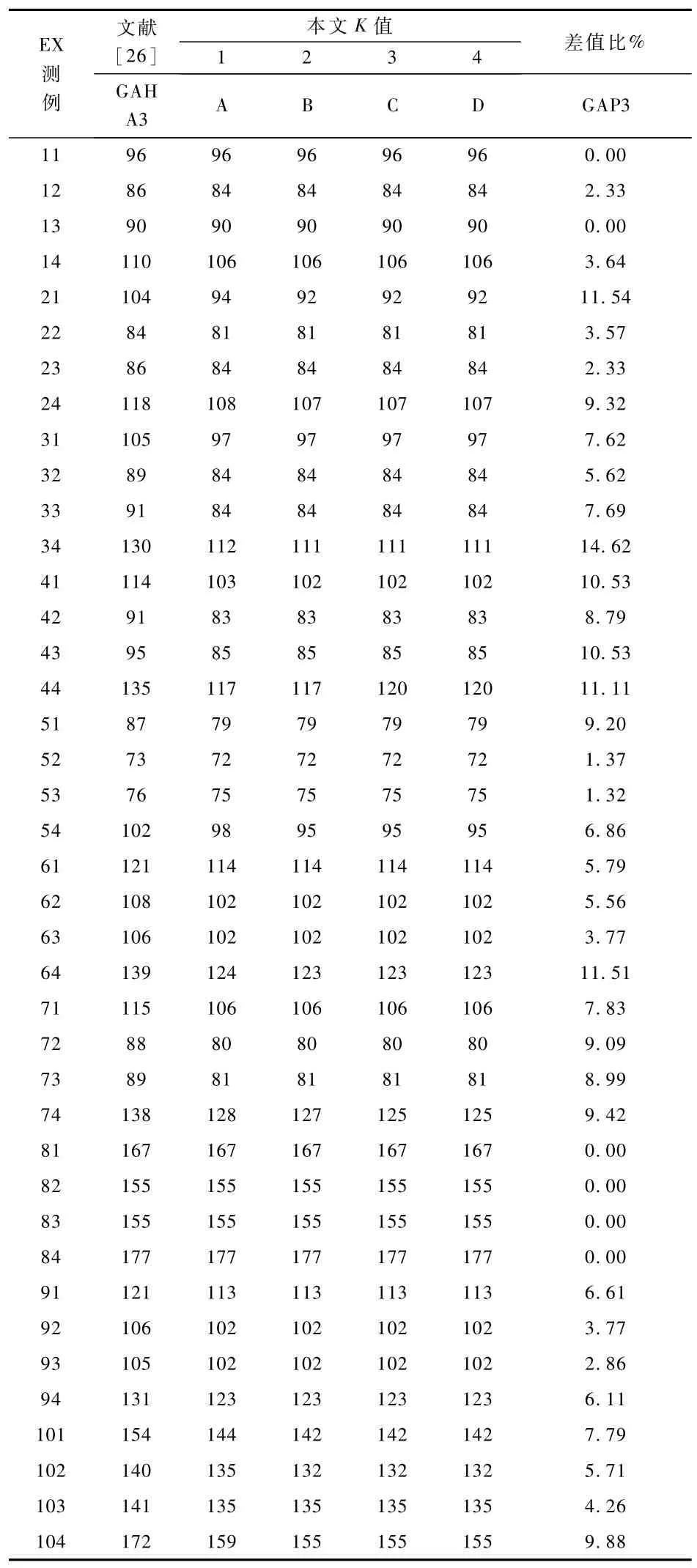
表2 实验及对比结果(h=3)
从表2中的数据可知,G-ABC算法100%的运行结果不差于GAHA3的最优解,85%的运行结果优于GAHA3的最优解,由此进一步说明了G-ABC算法的有效性。综合表1和表2的运行结果,分析其产生原因如下:
(1)G-ABC算法在选择搬运设备时,选择最早可到达的搬运设备,这有利于已加工完成的工件尽早被搬运,缓存区和加工设备尽早可用,提高了加工与搬运效率。
(2)启发式信息的设计,避免了G-ABC算法在增加输入/输出缓存区容量时,因解空间的扩大导致算法在解码过程中盲目搜索而降低运行效率的问题。
(3)采用角色互换机制的人工蜂群算法,在搜索过程中,将当前搜索结果最差的引领蜂转换为跟随蜂,加强了局部搜索能力。当有优于当前全局最优的结果出现时,恢复初始引领蜂的设置数量,可避免陷入局部最优。这不仅克服了标准人工蜂群算法中参数设置过多和搜索效果差的问题,而且兼顾了全局广泛寻优和局部精确寻优。
3.3 缓存区灵敏度分析
从表1和表2中,不难发现,部分测例随着缓存区容量增大,最优值减小。以EX74测例为例,为了排除种群规模N设置过小,而导致未能全局充分搜索的影响,进一步将种群规模N 增大为5000,重复表2的实验过程,发现EX74测例的运行结果仍为表2中所示,并以此绘制出如图5所示的随缓存区容量K变化的最优值变化图。
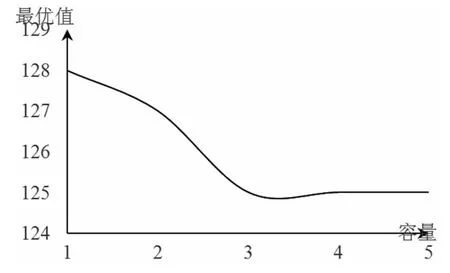
图5 不同K值下的最优值变化
从图5中可以看出,随着缓存区容量的增大,最优值在逐步减小,在缓存区容量为从1逐渐变为3的过程中,最优值在逐渐减小,当缓存区容量设为4和5时最优值不再减小。这说明缓存区容量在一定范围内影响调度过程,当缓存区容量达到一定数量时,不再是调度过程的制约因素。对于工序数量多的测例,缓存区的容量在调度过程中的影响更为明显。
3.4 启发式信息有效性分析
为验证启发式信息的有效性,设计了去掉启发式信息的具有角色互换的人工蜂群算法(P-ABC)。以EX14等5个测例为例,将搬运设备设置h=2,缓存区设置h=1,每组测例运行20次,取其结果平均值,比较P-ABC和G-ABC的运行结果。算法运行环境参照3.1节,种群规模N均为1000,运行结果见表3。其中,A列和B列分别表示P-ABC和G-ABC20次运行结果的平均值;GAP4列表示P-ABC和G-ABC的差值比,计算方式:GAP4=(A-B)/A*100%,若GAP4>0,说明G-ABC优于P-ABC。
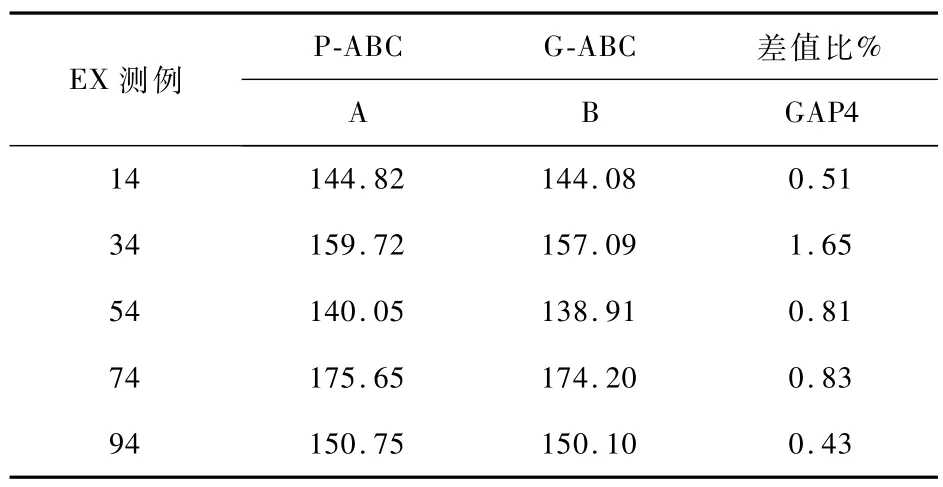
表3 启发式信息对运行结果影响对比
从表3中可以看出,5个测例的差值比最大为1.65%,最小为0.43%,平均差值比为1.04%,说明G-ABC的平均运行结果优于P-ABC,即说明了启发式信息的有效性。
4 结束语
考虑有限缓存区的Job Shop加工与搬运集成调度问题是对传统作业车间调度问题(JSP)的扩充,更是对仅考虑搬运设备和仅考虑有限缓存区JSP的完善,并且更具复杂性和实践应用性。本文的研究表明:
(1)采用角色互换的人工蜂群算法,克服了标准人工蜂群算法中参数设置过多和搜索效果差的问题,引入引领蜂和跟随蜂角色互换机制可以更好的兼顾全局广泛搜索和局部精确搜索。
(2)在一定范围内,缓存区容量设置在调度过程中会影响调度结果,尤其对于工序数多的测例影响更为明显。
(3)在缓存区容量一定的条件下,如何优先解码加工任务和搬运任务是优化该问题的关键。而针对此设计的启发式信息,可以提高算法的寻优效率。
(4)通过仿真实验,算法参数取值具有一定范围。进一步,通过与其他算法比较,验证了该算法有较好的求解能力。
这类问题的解决能够为企业提供更多灵活实用的调度方案,进而提高企业生产力。
