无线传输中短码长喷泉码的度分布优化算法*
2016-11-02李杰
李 杰
无线传输中短码长喷泉码的度分布优化算法*
李 杰**
(上海工程技术大学高等职业技术学院,上海 200437)
数字喷泉码是针对大规模网络数据分发而提出的一种新的信道编码方式。度分布是决定数字喷泉码译码性能的关键因素。为提高译码性能,针对应用于无线信道的喷泉码提出了一种度分布优化的算法。首先,根据理想孤子分布和鲁棒孤子分布产生度值序列,然后将该度值序列截短,在此基础上根据优化算法求解该序列中每个度值的最优概率,最后得到优化的度分布。仿真结果表明,本算法产生的度分布进行编译码产生的误码率低于鲁棒孤子分布和固定度分布,提高了译码性能。
无线传输;信道编码;数字喷泉码;LT码;度分布;优化算法
1 引 言
无线传输中为了对抗噪声干扰和信道变化,通常采用自动重传请求(Automatic Repeat Request,ARQ)来实现数据在无线通信网络中的可靠传输。然而ARQ技术要求系统中有反馈信道,在很多情况下系统中不存在反馈信道,比如广播信道。即使存在反馈信道,当用户数量较多时,大量用户的反馈数据将形成“反馈风暴”,甚至导致网络瘫痪。
喷泉码是一种新型的前向信道编码[1]。对于给定的输入信号,发送端可以按照接收端的需要生成任意数量的编码包,接收端只要接收到其中任意足够的编码包就能译码得出源数据包,并且不用考虑接收顺序问题,因此喷泉码也被称为无码率编码。喷泉码只要接收到充足的数据,即便数据的顺序是混乱的,接收机也可以正确地解码恢复源数据。喷泉码不依赖反馈信息的特点很适合在无线信道中传输。
2002年,Luby[2]提出了第一个实用数字喷泉码LT码(Luby Transform Codes)。该编码算法简单,具有较低的运算复杂度,编码性能主要由度分布决定。在文献[2]中Luby也提出了构造度分布的方法并且设计了两种实用的度分布,即理想孤子分布(Ideal Soliton Distribution)和鲁棒孤子分布(Robust Soliton Distribution)。这两种度分布在数据包较大时译码性能较好,当数据包长度趋于无穷时,译码性能也接近最优;数据包长度较小时,由于实际度分布常常不满足度分布函数,因而译码失败概率较高,译码性能下降。针对这一问题通常可以通过接收更多的码字来完成译码,但增加码字需要较多的内存和CPU资源,在一些资源受限的场合并不适用,比如无线多媒体传输中移动设备的内存和CPU资源就相对有限[3-4]。针对这一问题,本文对短数据包应用环境下度分布的优化进行了研究。
度分布的优化方面已有一些研究成果。文献[5]提出了利用马尔科夫链优化度分布的算法,通过递归算法对最大长度达到20个块的信息包推导出了最优的度分布;该算法复杂度较高。文献[6]提出了改进的鲁棒孤子分布,通过调整度分布中1度值和2度值的选择概率,降低方差,增加译码成功概率;该算法只对度值1和度值2的选择概率进行了调整,没有优化其他度值的选择概率。文献[7]中采用斐波那契数列作为度值序列,将度值的选取概率看作是判决变量,将译码性能看作是优化目标,求解能够使译码性能最优的度分布。文献[8]提出了对不同码长的输入源进行度分布优化的实际架构。文献[9]提出了一种适用于反馈喷泉码的基于部分信息度分布构造方法。针对无线传输,本文研究了短喷泉码的度分布优化算法,通过缩小度值的取值范围和优化度值的选择概率得到适合短喷泉码的度分布。
2 LT码
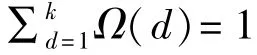
当译码器接收到N个码字y1,y2,…,yN后开始译码,N≈k。首先在接收到的码字中寻找度为1的码字yi,令译码器输出xi=yi,然后对所有与xi相接的yi进行异或运算,yj=yj⊕xi并与xi相接的节点度值减1。重复上述步骤直到所有xi都恢复。如果没有度值为1的码字或存在未被恢复的码字,则说明接收端必须接收更多的码字才能完成译码。LT码编码或译码k个码字大概需要进行klgk次异或运算。
3 度分布
喷泉码的度分布设计是决定译码性能的关键,在编码过程中度值的选择至关重要,它决定了有多少输入码字用于产生一个输出码字。一旦度值被确定,相应的个数的输入符号被随机挑选出来进行异或。一个好的度分布能使接收端用尽可能少的接收符号和尽可能小的复杂度恢复出原始信息。喷泉码译码的开始取决于接收信息中d=1节点的分布,之后如果在迭代过程中可持续产生d=1节点,译码就可以顺利开展。通常大部分的节点的度值应该较小,以减少译码整体的冗余运算并保证译码过程的持续进行;少量节点应该度值较大,以增加迭代更新提高正确性。
3.1理想孤子分布
Luby提出的理想孤子分布是喷泉码最理想的度分布。每次迭代译码都保证恢复出一个符号,并产生一个新的d=1的节点,这样既保证了译码的顺利进行又使得译码运算次数最少。该分布定义如下:

式中:d表示度值;ρ(d)表示度值d的选择概率。
但是在实际应用中,由于数据长度有限,编码时度分布无法精确符合理想分布,因此在解码过程中很容易丢失d=1的节点,导致译码无法开始,或是在后续迭代中无法产生新的d=1的节点导致译码失败。因此,Soliton分布实际性能并不够理想。
3.2鲁棒孤子分布
由于理想孤子分布的不足,Luby提出了改进的度分布,也就是鲁棒孤子分布。鲁棒孤子分布定义如下:

式中:参数c和δ是两个大于0的参数,用来保证在译码过程中d=1的节点数量能够达到期望值。该分布有效地结合理想孤子分布的的优点,只需k+个编码码字就可以以至少1-δ(δ∈(0,1])的概率正确恢复出原码字[2]。
4 无线信道中的度优化
Luby提出的理想孤子分布和鲁棒孤子分布采用随机方式进行编码,通常在数据包达到104或更高量级时才能取得良好的编译码性能,而在无线信道中数据包较短,使得编码符号的实际度分布与设定的度分布很可能不一致,从而导致译码的失败。针对这一问题,本文提出了针对短喷泉码的度分布优化算法,通过缩小度值的取值范围和优化短数据输入条件下度值的选择概率得到适合短喷泉码的度分布。
为了确保接收端接收到最少的数据后就可以成功解码,需要每个编码码字携带的信息对接收端而言都是有用的,因此要求度值较高;而在译码中BP算法中需要度值为1的编码码字,因此度值越低,度为1的码字出现概率也就越大,译码成功率越大,因此要求度值越低越好。这两个条件对度的要求相互矛盾,因此度分布的设计需要均衡这两者的要求,寻找折衷的方案[10]。本文提出了一个适合于不同输入信号的度值选择算法,以获得更好的译码性能。
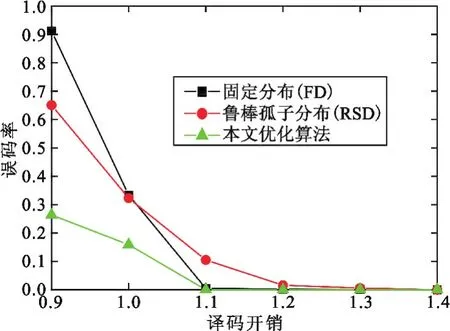
理想孤子分布或鲁棒孤子分布中度值的取值范围从1到k,dI∈DI,DI={1,2,…,k},其中k是输入数据长度,DI是度值的集合。当数据较长时,就会产生较大的度值,同时该度值的选择概率很小。以k= 2 000为例,大于500的度值对应的概率只有10-6量级,该度值被选择用来编码的可能性很小,可以忽略不计。因而需要缩小度值的范围,截短度值序列。定义概率门限p1将理想孤子分布或鲁棒孤子分布的每个度值对应的选择概率和门限相比较,如果一个度值dI的选择概率大于门限,即ΩI(dI)>p1,其中Ω表示概率,ΩI(dI)表示度值dI被选择概率,那么该度值被保留,否则将该度值从DI中删除。由于这两种分布在度值较大区域是递减函数,因此当某个度值的选择概率小于给定门限后,比该度值大的其余度值对应的概率也一定小于门限,这些度值都将删除,度值集合也被截短。将截短的度值集合表示为dt∈Dt,Dt={1,2,…,m},m 综上所述,度值选择算法的主要步骤如下: 第1步 初始化参数p1,p2,w,累加概率s=0和目标度值集合D={}; 第2步 对给定的数据长度产生理想孤子分布(或鲁棒孤子分布)ΩI(dI),dI∈DI; 第3步 根据门限p1对度值集合进行截短,得到Dt; 第4步 将Dt中的度值所对应的概率ΩI(dt),dt∈Dt和门限p2相比较,如果概率大于门限,跳至第5步;如果概率小于门限,则 (1)计算加权概率和s=s+ΩI(dt)×w,将s和门限p2比较; (2)如果大于门限,将dt加入目标度值集合;否则,检查下一个度值dt+1; (3)重复上两步直到s≈p2; 第5步 将当前的度值加入到目标度值集合中并置概率和s=0; 第6步 重复第4~5步,检查Dt中其余的度值,直到所有度值都检查完毕。 在该算法中p1用来截短度值序列。如果p1=0,那么所有初始的度值都会被保留下来Dt=DI。p1越大,被删除的度值越多,保留的度值越少。同时由于去除了部分度值,因此截短后的度值集合Dt中所有度值的概率和小于1。但是,由于删除度值的概率非常小,因此Dt中所有度值的概率和可以近似为1。比如当k=1 000、p1=0.000 1时,所有保留的度值的概率和为0.991;k=4 000、p1=0.000 1时,所有保留的度值的概率和为0.990 2。门限p2的选择同样影响最终的度值集合,p2越大,被删除的度值越多,保留的度值越少,目标度值集合越小。 根据上述算法确定度值后,每个度值的选择概率也相应确定,但此时的概率一定不是最优的,还要进一步对概率分布进行优化。在无线信道传输中,由于传输错误,LT译码端通常不能将所有码字正确译码。因此度概率分布的设计目标是获得一组最优的概率分布,使得接收端可以以最小的开销恢复出最多的码字。这个问题可以转化为在给定开销OB的条件下,求解能够使译码码字最多的概率分布: 式中:ber(Ω,d)是该概率分布条件下的误码率;O是开销。上式所表示的最优化问题可以通过全局搜索求解,例如可以使用进化策略搜索最优的概率分布。 度分布优化算法的实验分为两步。首先,根据度值算法确定合理的度值,以输入数据k=300为例进行实验,选取不同的门限时,得到的度值不同: 确定度值后再对度值的概率分布进行优化,就能够得到在该度值集合下最优的译码性能。 第二步,求解度值集合中度值的最优选择概率,得到优化的度分布。将本算法优化得到的度分布的译码性能和固定度值分布以及鲁棒孤子分布的性能进行了比较。其中固定度值分布是一种使用较为广泛的度分布[12],相应的多项式为 该度值分布具有较好的译码性能。 本文分别在固定数据包长度和固定译码开销的条件下对算法的译码性能进行了测试。根据Luby的算法,鲁棒孤子分布中的参数c和δ分别取0.5和0.03[2]。设定度值的最优选择概率算法迭代200次。由于无线信道上数据包较短,不失一般性的定义固定数据包的比特长度为1 000。不同开销条件下的译码性能如图1所示,其中横坐标的译码开销表示发送端实际发送的数据包与源数据包的比值,纵坐标表示此条件下的误码率。从图1可以看出随着译码开销的增大,误码率减小,同时在相同开销下,本算法得到的度分布编码后的误码率低于鲁棒孤子分布和固定度分布,具有最好的译码性能。图2还在译码开销为1的条件下对不同长度的编码包进行了测试,从图中可以看出此时本算法得到的度分布编码优于鲁棒孤子分布和固定度分布。由于误码率随着译码开销的增大而减小,当译码开销较大时,本算法的优势不明显;在开销较小时,短码长喷泉码使用本文的优化算法能够得到更好的译码性能。 图1 不同开销条件下译码性能比较Fig.1 BER of different algorithms versus decoding overhead 图2 不同数据长度条件下译码性能比较Fig.2 BER of different algorithms versus data length 通常传输的信息不具有同等的重要性,比如无线网络中控制信号要比用户数据更重要。而无线通信是一个噪声信道,因此为了保护传输数据中更重要的那部分信息通常采用不等差错保护的传输方式。本文也测试了在不等差错保护的传输模式下优化后的度分布的译码性能。不等差错保护采用的是基于喷泉码的扩展窗方案[13],根据该保护方案,按照重要性将数据分为两个等级,重要数据和非重要数据,其中重要数据占总数据的25%。在此平台上对固定分布、鲁棒孤子分布和本文所提的优化分布的译码性能分别进行了测试,如图3所示,可以看出在不等差错保护的编码平台下本文的算法同样具有最好的译码性能。图4显示了不等差错保护条件下,重要数据在不同开销条件下译码后的误码率,可以看出由于得到了更多的保护,这部分数据的误码率较低,同时本文的算法得到的误码率也是所比较算法中最低的。 图3 不等差错保护条件下译码性能比较Fig.3 BER of different algorithms versus decoding overhead under unequal error protection 图4 不等差错保护条件下重要数据译码性能比较Fig.4 BER of important data versus decoding overhead under unequal error protection 本算法由度值的确定和度分布的优化两部分组成,其中度值的确定计算量很小,度分布的优化计算量较大,算法的复杂度主要集中在度分布的优化部分。当数据包长度为1 000 b时在2.7 GHz Intel i5处理器的计算机上对不同迭代次数的耗时和误码率进行测试,结果见表1。可以看出度值选择算法的复杂度和迭代次数无关,并且计算量很小;度分布优化算法的计算量和迭代次数成正比,但是误码率并不会随迭代次数的增加有明显降低。 表1 迭代次数和耗时的比较Tab.1 Number of iterations versus computing time 喷泉码是一种新型的低密度无码率信道编码码字,并得到了广泛应用。但喷泉码在短码长编码时性能不佳,成为了喷泉码在无线通信中应用的瓶颈。针对这一问题,本文在通过分析度分布对无线传输中喷泉码编译码的影响,提出了一种数字喷泉码中度分布的优化算法。该算法先根据设定的门限值确定度值的集合,然后通过优化算法求解每个度值的最优概率。仿真结果表明,在相同数据包长度下,使用本算法产生的度分布进行LT编码得到的误码率低于鲁棒孤子分布和固定度分布,同时当数据包长度改变时,本算法产生的度分布仍然具有最优的译码性能。本算法能够提高短码长喷泉码的译码性能,对喷泉码在无线传输上的应用具有参考价值。算法有一定复杂度,未来还可进一步研究降低复杂度的方法。 [1] BYERS J W,LUBY M,MITZENMACHER M,et al.A digital fountain approach to reliable distribution of bulk data[C]//Proceedings of the ACM SIGCOMM′98 Conference on Applications,Technologies,Architectures,and Protocols for Computer Communication.New York:ACM,1998:56-67. [2] LUBY M.LT codes[C]//Proceedings of 2002 IEEE Symposium on Foundations of Computer Science.Vancouver,Canada:IEEE,2002:271-280. [3] 于国海,王呈贵,张哲.采用喷泉码的无线协同多跳信息累积广播协议[J].电讯技术,2011,51(3):84-88. YU Guohai,WANG Chenggui,ZHANG Zhe.Cooperative multi-hop broadcast protocols using fountain codes for wireless networks[J].Telecommunication Engineering,2011,51(3):84-88.(in Chinese) [4] 姚渭箐,易本顺.喷泉码在认知无线电网络中的应用[J].电讯技术,2015,55(8):935-941. YAO Weiqing,YI Benshun.Application of fountain code in cognitive radio network[J].Telecommunication Engineering,2015,55(8):935-941.(in Chinese) [5] HYYTIA E,TIRRONEN T,VIRTAMO J.Optimal degree distribution for LT codes with small message length[C]// Proceedings of 2007 26th IEEE International Conference on Computer Communications.Anchorage,AK:IEEE,2007:2576-2580. [6] TSAI P C,CHEN C M,CHEN Y P.A novel evaluation function for LT codes degree distribution optimization[C]//Proceedings of 2014 IEEE Congress on Evolutionary Computation(CEC).Beijing:IEEE,2014:3030-3035. [7] CHEN C M,CHEN Y P,SHEN T C,et al.On the optimization of degree distributions in LT code with covariance matrix adaptation evolution strategy[C]//Proceedings of 2010 IEEE Congress on Evolutionary Computation.Barcelona:IEEE,2010:1-8. [8] CHEN C M,CHEN Y P,SHEN T C.A practical optimization framework for the degree distribution in LT codes[J].IEICE Transactions on Communications,2013,96(2):2807-2815. [9] 牛芳琳,李宝明,陈付亮,等.一种改进的基于部分信息喷泉码度分布设计[J].电子学报,2016,44(2):295-299. NIU Fanglin,LI Baoming,CHEN Fuliang,et al.The improved degree distribution for rateless code under partial information[J].ACTA Electronica Sinica,2016,44(2):295-299.(in Chinese) [10] 邹衍芳.无线多媒体传输中喷泉码技术研究[D].北京:北京邮电大学,2013. ZOU Yanfang.Research on fountain codes technology in wireless multimedia transmission[D].Beijing:Beijing University ofPostsandTelecommunications,2013.(in Chinese) [11] TSAI P C,CHEN C M,CHEN Y P.Sparse degrees analysis for LT codes optimization[C]//Proceedings of 2012 IEEE World Congress on Computational Intelligence. Brisbane,Queensland,Australia:IEEE,2012:1-6. [12] SHOKROLLAHIM A.Raptor codes[J].IEEE Transactions on Information Theory,2003,52(6):2551-2567. [13] BOGINO M,CATALDI P,GRANGETTO M,et al.Expanding window fountain codes for unequal error protection[C]//Proceedings of 41st Asilomar Conference.Pacific Grove:IEEE,2007:1020-1024. 李 杰(1975—),女,吉林白山人,2001年于长春理工大学获硕士学位,现为上海工程技术大学高级工程师,主要从事无线通信网络、光通信网络等方面的研究。 LI Jie was born in Baishan,Jilin Province,in 1975.She received the M.S.degree from Changchun University of Science and Technology in 2001.She is now a senior engineer.Her research concerns wireless communication network and optical communications. Email:stslijie@163.com A Degree Distribution Optimization Algorithm for Small Size Fountain Codes in Wireless Transmission LI Jie Digital fountain code is a popular class of erasure code,which is often used in the case of large network data transmission.The performance of Luby Transform(LT)code is mainly decided by the degree distribution.To improve the decoding performance,a degree distribution optimization algorithm is designed for wireless transmission.Firstly,based on classical soliton distribution and robust soliton distribution,the set of degree values is determined.Then the degree distribution that minimizes the number of un-recovered source symbols is found.The optimal degree distribution can be solved by evolutionary strategy.The experimental results show that compared with LT code with robust soliton distribution and the fixed degree distribution,the proposed algorithm improves the number of the recovered symbols obviously with the same overhead. wireless transmission;channel coding;digital fountain code;LT code;degree distribution;optimization algorithm **通信作者:stslijie@163.com stslijie@163.com TN911.2 A 1001-893X(2016)08-0900-06 10.3969/j.issn.1001-893x.2016.08.012 2016-01-19; 2016-05-10 date:2016-01-19;Revised date:2016-05-10 引用格式:李杰.无线传输中短码长喷泉码的度分布优化算法[J].电讯技术,2016,56(8):900-905.[LI Jie.A degree distribution optimization algorithm for small size fountain codes in wireless transmission[J].Telecommunication Engineering,2016,56(8):900-905.]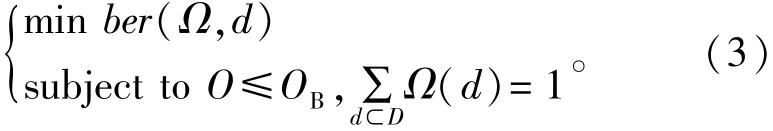
5 实验结果






6 结束语

(Advanced Vocational Technical College,Shanghai University of Engineering Science,Shanghai 200437,China)
