粒子射流喷射钻塞流场特性及参数优化

赵 健, 徐依吉, 孙宝京, 常方瑞, 韩晓强

(1.中国石油大学(华东)东营科学技术研究院,山东东营 257061; 2.中国石油大学(华东)石油工程学院, 山东青岛 266580; 3.中国石化胜利油田分公司油气井下作业中心,山东东营 257000)

随着油田开发的不断深入,为满足开发井网需求,打塞封层、水泥堵炮眼、油水井眼窜封堵、长停井恢复生产等工艺技术是老井恢复产能、挖掘剩余油潜力、提高储量动用程度的重要措施[1-3]。这些开发工艺将产生水泥塞面,需要通过钻塞作业钻除。目前常规钻塞采用转盘或螺杆钻带动钻头钻进,但存在着钻塞进尺慢、浅层钻塞加压困难、套损井无法施工、小井眼井易卡钻、易造成井下复杂事故等问题[4-5]。近年来发展的粒子射流技术是提高破岩效率的有效途径之一,该技术通过在高压水射流中加入一定比例的粒子,形成高速粒子射流冲击到岩石表面,在冲击区域形成瞬时极大的冲击应力,可实现岩石的高效破碎[6-13]。因此针对常规钻塞方法存在的难题,提出一种粒子射流喷射钻塞技术,该技术具有工具尺寸小、喷射井眼规则、钻进速度快等优势,其中如何充分利用粒子射流能量,实现井底粒子射流全覆盖,并避免对套管壁的冲蚀是目前该技术面临的最大难题。笔者基于计算流体力学欧拉-拉格朗日方法,建立粒子射流喷射钻塞数值模型,阐明井底流场结构特性,优化设计钻塞参数,并进行全尺寸试验验证。

1 计算流体力学模型

粒子射流喷射钻塞技术通过固液两相粒子射流高速喷射钻进水泥塞,粒子为固相,体积分数小于10%,流体为液相。采用固液两相流离散相(discrete phase model,DPM)模型,通过Fluent软件求解[14-15],将流体假设为连续流动介质,粒子为离散、不连续的固体颗粒介质,即流体为连续相,粒子为分散相;对连续相求解采用Euler方法,对分散相描述采用Lagrange方法[16-18]。

1.1 控制方程

1.1.1 液 相

定义液相为不可压缩流体,其流动方程用连续性方程和N-S方程[17-19]表示为

(1)

(2)

式中,ux、uy和uz分别为流体在x、y、z方向上的速度;fX、fY和fZ分别为流体在x、y、z方向上的质量力;t为流过单元体的时间;p为静压力;μ为流体黏度。

流体流动模型选择常用的k-ε标准模型[17-19],即:

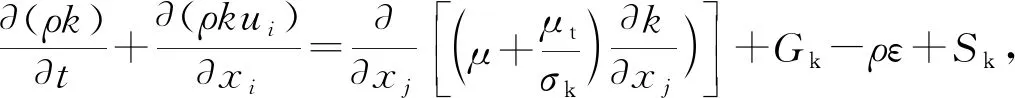
(3)

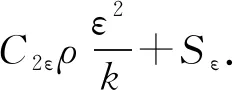
(4)

其中

式中,k为湍动能;ui为i方向上的速度分量;Gk为平均速度梯度产生的湍动能;ε为湍动耗散率,m2/s3;xi和xj为空间坐标;σk和σε分别为k和ε的湍流普朗特数;μt为湍动黏度,mPa·s;C1ε和C2ε为常数;Cμ和σε为源项。

1.1.2 离散相

通过在Lagrange坐标系求解粒子的运动方程可得到粒子运动轨迹,粒子运动由牛顿第二定律控制,这里仅列出颗粒在x方向的受力控制方程为

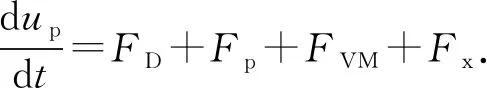
(5)

其中

式中,FD、Fp、FVM和Fx分别为粒子单位质量拽力、压力梯度力、附加质量力和其他外力之和;μf为流体动力黏度;ρp为粒子密度;dp为粒子直径;CD为阻力系数;Rep为粒子雷诺数;up为粒子速度;a1、a2和a3分别为和雷诺数有关的光滑球形粒子常数,由Morsi和Alexander[20]得出。

Fx为其他外力之和,主要包括Basset力、Saffman 升力、Magnus升力等作用力。由于横向速度梯度(剪切层流动)使粒子产生旋转引致的Saffman升力和Magnus升力,仅对亚观颗粒(直径为1～10 μm)有效,由于本文中粒子粒径(约1 mm)较大,在进行数值模拟时近似忽略了粒子的自身旋转效应[22]。单位质量粒子所受的Basset力为

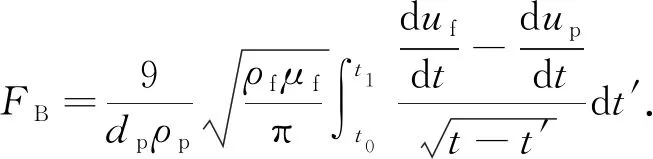
(6)

1.1.3 磨损方程

影响固液两相流冲蚀磨损速率的主要参数包括水力参数、材料性质、粒子性质和流体特性。Huser和Kvernvold等[23-24]提出的入射角磨损方程已经被计算流体力学广泛采用,来计算固液两相流的冲蚀磨损速率:

(7)

其中

f(θ)=2.69θ+1.61θ2-8.84θ3+7.33θ4-1.85θ5,

C(dp)=0.434B-0.59×10-7.

式中,Rerosion为磨损速率;N为冲击到壁面的粒子数;mp为粒子质量流量;C(dp)为粒子直径的函数;θ为粒子冲击壁面的冲击角度;f(θ)为冲击角度的函数;b(v)为粒子的速度指数函数;Aface给定区域的壁面面积;θ为颗粒对壁面的冲击角(入侵角);B为被冲击材料的布氏硬度,本研究中水泥石布氏硬度取0.6[25]。

1.2 几何建模及边界条件

依据油田常用的139.7 mm套管尺寸,利用三维绘图软件SolidWorks 2015建立粒子射流喷射钻塞三维模型,套管内径为121 mm,长度为200 mm,喷嘴高度为10 mm,如图1(a)所示。粒子射流钻塞工具实物模型如图1(b)所示,工具外径90 mm。将建立的物理模型导入到Gambit 2.4.6软件中完成网格划分,如图1(c)所示。将网格划分模型再导入ANSYS Fluent 15.0软件中,温度设为25 ℃,湍流强度设为3%,壁面粗糙度设为10 μm[24],粗糙度常数设为默认值0.5,壁面边界设为“反射(reflect)”,出口边界设为“逃脱(escape)”。为了改善拟合收敛性,压力场和速度场计算采用SIMPLEC算法,每个方程的控制量残差为小于10-5,或者迭代次数小于5 000,压力项采用标准化离散方法,对流和扩散项采用二阶迎风离散方法。设定入口流速为115 m/s,粒子质量流量为0.8 kg/s,粒子入射速度为115 m/s。

图1 粒子射流喷射钻塞模型Fig.1 Model of drilling cement plug with particle waterjet

2 井底流场特性

通过对粒子射流喷射钻塞过程的模拟分析,分析粒子在流场中的运动轨迹,揭示井底速度场、压力场的分布规律,阐明井底流场结构特性。模拟条件为粒子体积分数5%、粒径0.5 mm。

2.1 粒子运动轨迹

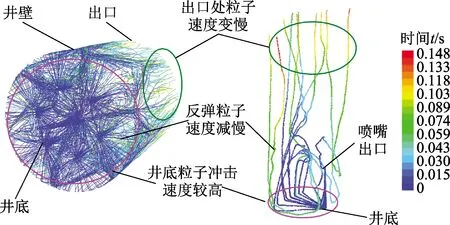
图2 井底流场中粒子运动轨迹Fig.2 Particle traces in bottom hole flow field

粒子射流由喷嘴高速喷出后,冲击破碎水泥塞面并反弹,最终从环空返出,运动轨迹如图2所示。0 s时粒子从喷嘴入口进入喷嘴内流道,在流体携带下由喷嘴出口高速喷出,进入井底环空中,以极高的速度冲击破碎井底水泥塞面,粒子速度逐渐降低,粒子冲击动能转化为水泥塞的破碎能,其速度降为零后粒子开始反弹[17-18],反弹粒子速度明显降低,最后反弹粒子在流体的携带下从环空返出。

2.2 井底速度场

井底速度矢量剖面如图3所示。由图3可得,粒子射流的井底流场分为自由射流区、冲击区、漫流区、上返区和漩涡区。粒子射流从喷嘴高速喷出,形成自由射流区;在冲击区,粒子射流以入口速度冲击到水泥塞面,在塞面产生极大的冲击应力,并在接触区域下部形成拉伸应力[7,13],由于水泥石的抗拉应力远小于抗压应力,当拉伸应力超过水泥石的抗拉应力后,水泥内部产生一系列拉伸裂纹,并在水射流“水楔”作用下,水泥石碎块逐渐剥离本体,实现了水泥石的高效破碎[11,13];冲击后的反弹粒子和流体沿着井底由冲击区中心向井壁流动,形成漫流区,漫流区有利于钻屑和粒子及时离开井底并上返;在漫流区上部由于反向粒子射流交汇和喷头阻挡作用,形成了漩涡区,漩涡区不利于水泥屑、粒子的及时上返,易导致水泥屑的重复破碎,影响粒子射流能量的有效利用;水泥屑和粒子不断运动,最终在流体的携带下由上返区离开井底。

图3 井底速度矢量剖面Fig.3 Velocity vector profile in bottom hole

2.3 井底压力场

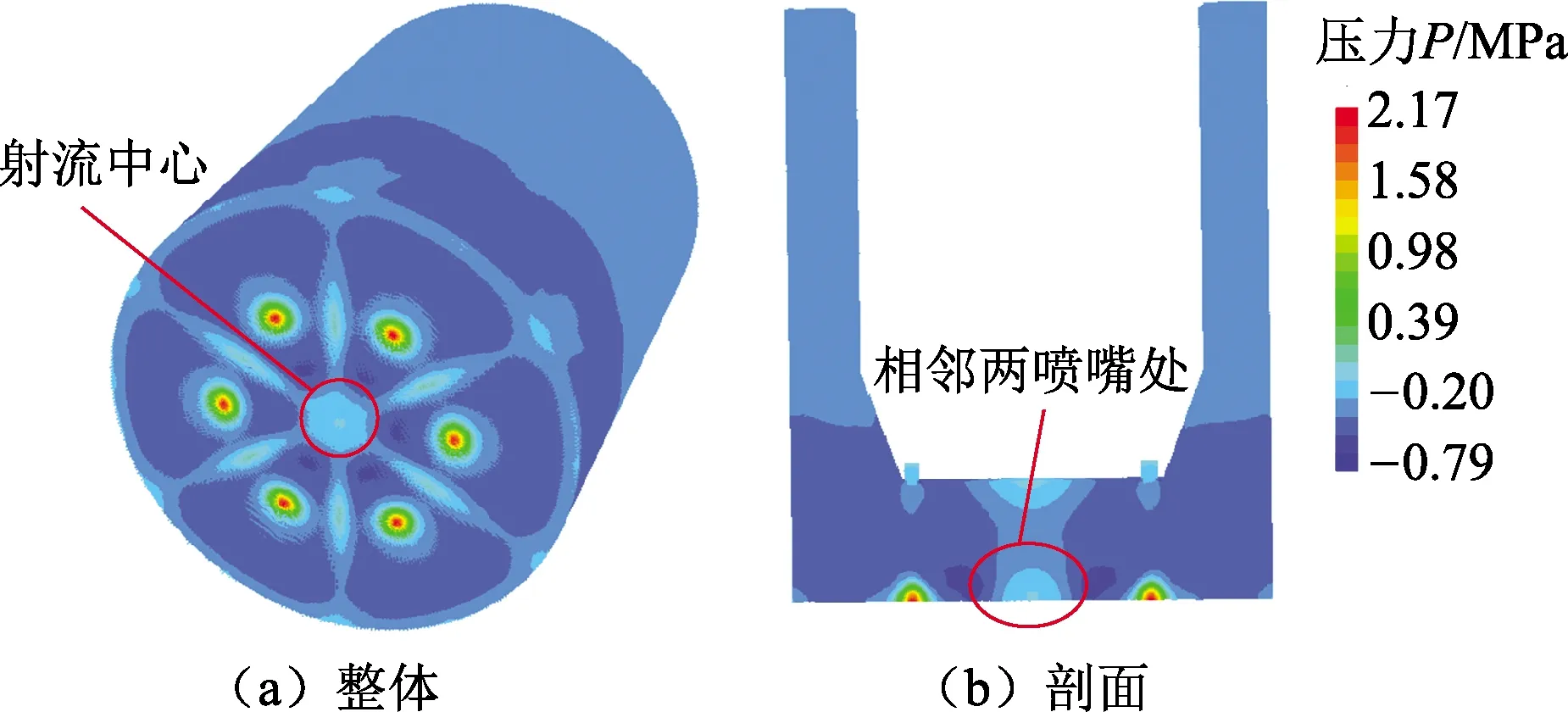
图4 井底压力云图Fig.4 Pressure nephogram in bottom hole

图4为粒子射流井底压力云图。井底最高压力分布在冲击区,即粒子射流冲击塞面的区域,该区域高速粒子射流冲击到塞面后,射流速度迅速降低,流体的动能转化为压能,此时流体压力最高,与伯努利原理吻合[16]。喷嘴位置对称井底压力场也对称(图4(a)),井底压力由射流中心处的最高值向四周减小,在两相邻喷嘴中心处,压力又逐渐升高,分析是由于两股方向相反的井底漫流撞击导致的压力升高(图4(b))。

3 钻塞参数优化设计

分析周向喷嘴个数、中心喷嘴、喷嘴倾斜角、喷距对水泥塞面冲蚀速率、井壁冲击力的影响,优化钻塞参数。

3.1 周向喷嘴个数

周向喷嘴个数是指粒子射流钻塞工具底面四周布置的喷嘴数量,喷嘴当量直径一定,不同周向喷嘴个数下粒子运动轨迹的分布如图5所示。随着周向喷嘴个数的增加,粒子射流在井底的覆盖范围逐渐增大,周向喷嘴增加至6个后,粒子射流即可覆盖至整个井底;但随着周向喷嘴个数的继续增加,相邻两喷嘴之间的距离减小,粒子射流之间的干涉碰撞增加[27],粒子轨迹变得紊乱,不利于粒子射流能量的充分利用,8个周向喷嘴时粒子轨迹已非常紊乱(图5(e)),因此从均匀覆盖井底和充分利用粒子射流能量两个方面来讲,6～7个周向喷嘴时效果较好。

平均冲蚀速率和最大单位面积冲蚀速率随周向喷嘴个数的变化如图6所示。随着周向喷嘴个数的增加,水泥塞的平均冲蚀速率先逐渐增加后减小,6个周向喷嘴时平均冲蚀速率最大。当周向喷嘴小于6个时,随着周向喷嘴个数的增加,粒子射流在井底的覆盖面积逐渐增加,粒子射流与塞面的冲击面积增加,因此冲蚀速率增加,喷嘴个数为6个时,水泥塞平均冲蚀率最大;当周向喷嘴数量超过6个后,两两喷嘴之间的距离过小,喷嘴间两股粒子射流之间发生相互干涉碰撞[10,12],减小了冲击到水泥塞面的粒子射流冲击总能量,因此水泥塞的平均冲蚀速率减小。8个周向喷嘴时由于喷嘴间距过近,射流间干涉严重,粒子轨迹非常紊乱(图5(e)),因此冲蚀速率受到严重影响。随着周向喷嘴个数的增加,水泥塞的最大单位面积冲蚀率先逐渐增加后减小,6个周向喷嘴时平均冲蚀速率最大,原因与平均冲蚀速率的变化一致。

图5 不同周向喷嘴个数下粒子运动轨迹分布Fig.5 Particles trajectory distribution with different circumferential nozzle number

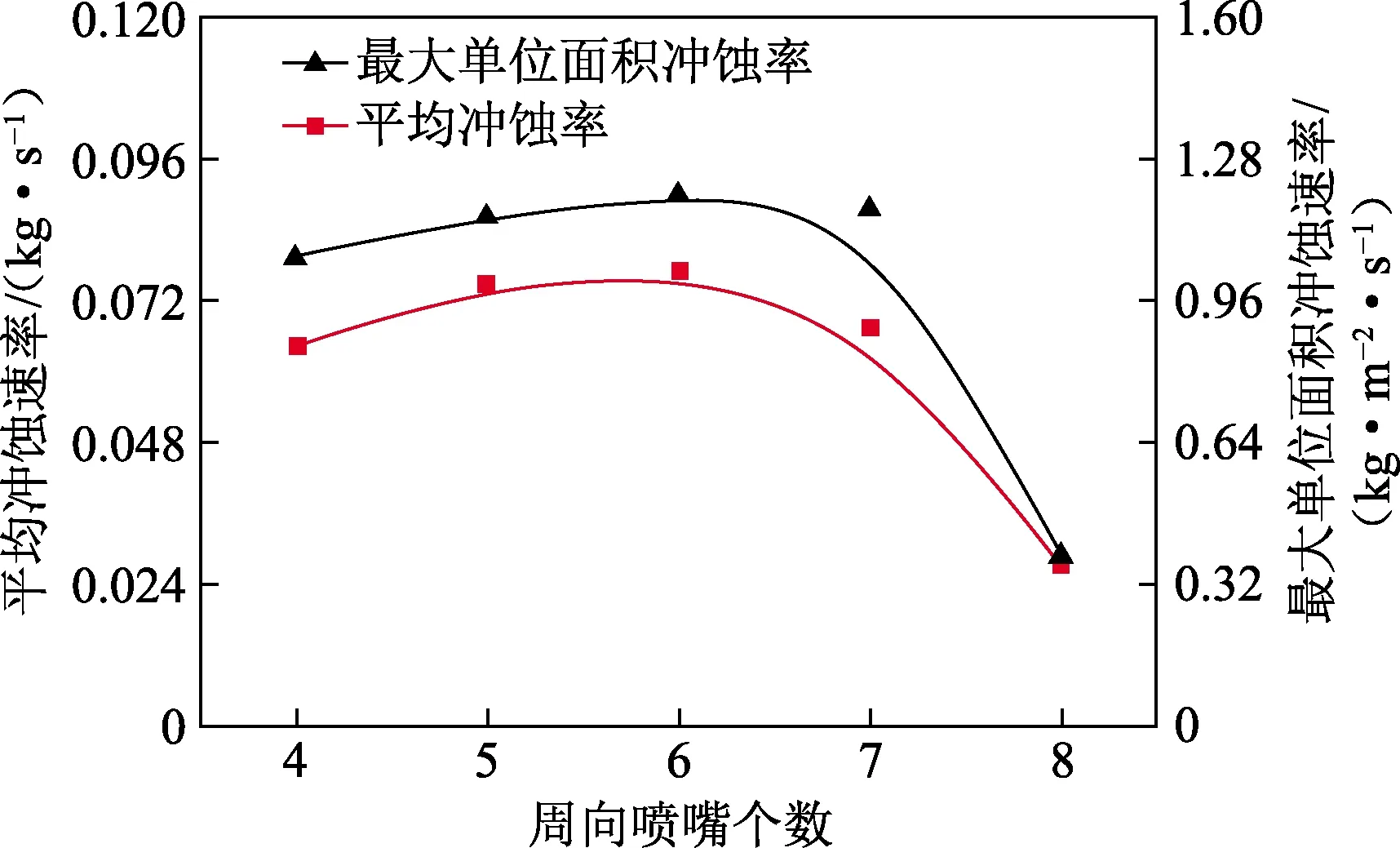
图6 平均冲蚀速率和最大单位面积冲蚀速率 随周向喷嘴个数的变化Fig.6 Average erosion rate and maximum unit erosion rate as a function of circumferential nozzle number

喷嘴当量直径一定,粒子射流对井壁冲击力随周向喷嘴个数的变化如表1所示。Xn和Zn分别是井筒水平面上相互垂直的两个坐标轴方向,冲击力通过ANSYS Fluent软件模拟结果的后处理分析得到,分别为两个方向上对壁面冲击力的合力。由表1可知,周向喷嘴为6～7个时,对井壁的冲击力最小。总排量和当量直径一定、周向喷嘴个数较少时,单个喷嘴直径变大,每个周向喷嘴喷出的粒子射流流量大,因此冲击到井壁的粒子概率较大,因此冲击力较大;当喷嘴个数增加后,单个喷嘴喷出的粒子射流流量减小,冲击到井壁的粒子减少,周向喷嘴6～7个时,冲击到井壁的粒子数量少,而且井底粒子射流相互之间干扰少,射流流动比较规律,粒子冲击破碎水泥塞后,能及时离开井底[17-18],因此对井壁的冲击小;但是当周向喷嘴数量继续增加,喷嘴间距过小,井底粒子射流运动规律变的非常紊乱,导致冲击到井壁的粒子量和冲击速度均增加,因此对井壁冲击力变大。综上分析,从井底覆盖率、冲蚀速率和对井壁冲击力3个方面考虑,周向喷嘴6～7个时钻塞效果最好。

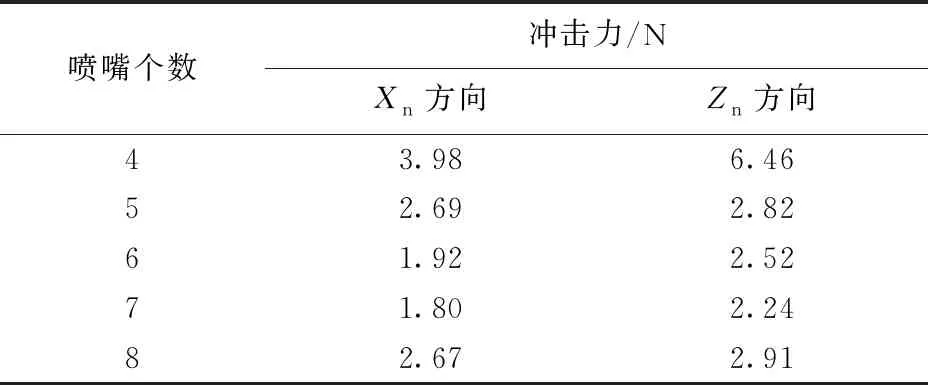
表1 粒子射流对井壁的冲击力随周向喷嘴个数的变化Table 1 Variation of impact force acted on well wall with circumferential nozzle number

3.2 中心喷嘴

无中心喷嘴速度分布云图及矢量图如图7(a)、(b)所示,可以看出当没有中心喷嘴时井底中心存在冲击速度较低区域,该区域粒子冲击速度较小,不利于中心水泥塞的破碎;而且无中心喷嘴时,井底中心的漩涡区域较大,易导致水泥屑的重复破碎,不利于水泥屑的及时上返,两方面均将导致钻塞速率减慢。增加中心喷嘴后,如图7(c)、(d)所示,井底中心处的低速区消除,粒子冲击速度均较高,井底中心的漩涡也明显减小减弱,更利于粒子射流能量的有效利用和水泥屑的及时离开井底[26],因此有助于钻塞速率的提高。

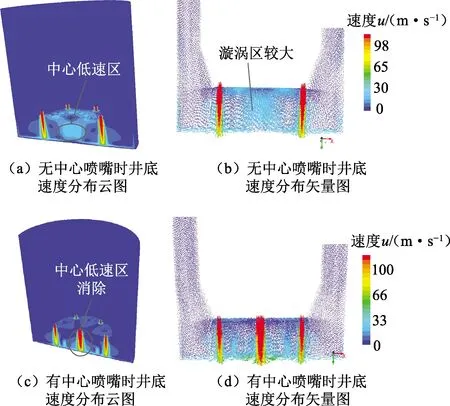
图7 有无中心喷嘴的速度分布Fig.7 Velocity profile with and without central nozzle in bottom hole

无中心喷嘴时,水泥塞平均冲蚀速率为0.076kg·s-1,最大单位面积冲蚀速率为1.2kg·m-2·s-1;有中心喷嘴时,水泥塞平均冲蚀速率为0.082kg·s-1,最大单位面积冲蚀速率为1.3kg·m-2·s-1。中心喷嘴加入后,水泥塞的最大单位面积冲蚀速率和平均冲蚀速率均增加,中心喷嘴加入后,消除了粒子射流井底流场中心的低速区,实现了井底中心处水泥塞的快速钻进,同时中心喷嘴减小减弱了井底中心处漩涡,更利于水泥屑及时离开井底,因此冲蚀速率增加。

无中心喷嘴时,粒子射流对井壁冲击力Xn方向上为1.95N,Zn方向上为2.83N;有中心喷嘴时,粒子射流对井壁冲击力Xn方向上为1.76N,Zn方向上为2.24N。中心喷嘴加入后,粒子射流对井壁的冲击力减小,当量直径一定时,中心喷嘴的增加,使粒子射流在井底中心处的喷射流量增加,而在四周喷嘴的流量减小,因此直接冲击到井壁上的粒子量减小,对井壁冲击力减小;同时由于中心漩涡的减小,岩屑更容易及时离开井底,减小了对井壁的冲击力。

3.3 喷嘴倾斜角

喷嘴倾斜角为工具中心轴线和喷嘴轴线之间夹角。倾斜角对于水泥塞的冲蚀速率和对井壁的冲击力影响较大。

平均冲蚀速率和最大单位面积冲蚀速率随倾斜角的变化如图8所示。随着喷嘴倾斜角α增加,平均冲蚀率先增加后减小,当倾斜角为5°时,平均冲蚀率最高。喷嘴倾斜角较小时,入射流体与反弹粒子之间碰撞干涉[27],射流垂直作用于井底,每个喷嘴射流也会相互干扰,影响粒子运移,不利于粒子射流冲击能量的充分利用;随着倾斜角的不断增加,入射粒子和反弹粒子两个方向的夹角增加,入射流体与反弹粒子之间碰撞减弱,同时由于向外倾斜角的增加,周向喷嘴之间、周向喷嘴和中心喷嘴之间的每股射流的干扰减小,粒子射流能量利用率提高[8,10,18],因此水泥塞的冲蚀速率增加;当倾斜角大于5°后,垂直作用到塞面的粒子速度分量迅速降低,导致对塞面冲击力降低,也不利于破碎塞面,因此冲蚀速率减小。最大单位面积冲蚀速率和平均冲蚀速率的变化趋势相同,当倾斜角为2.5°时最大单位面积冲蚀速率最大,分析是由于此时倾斜角小,在垂向方向的速度分量较高,对塞面同一位置的冲击力较大,此时粒子干涉也不严重,因此最大单位面积冲蚀速率最大。

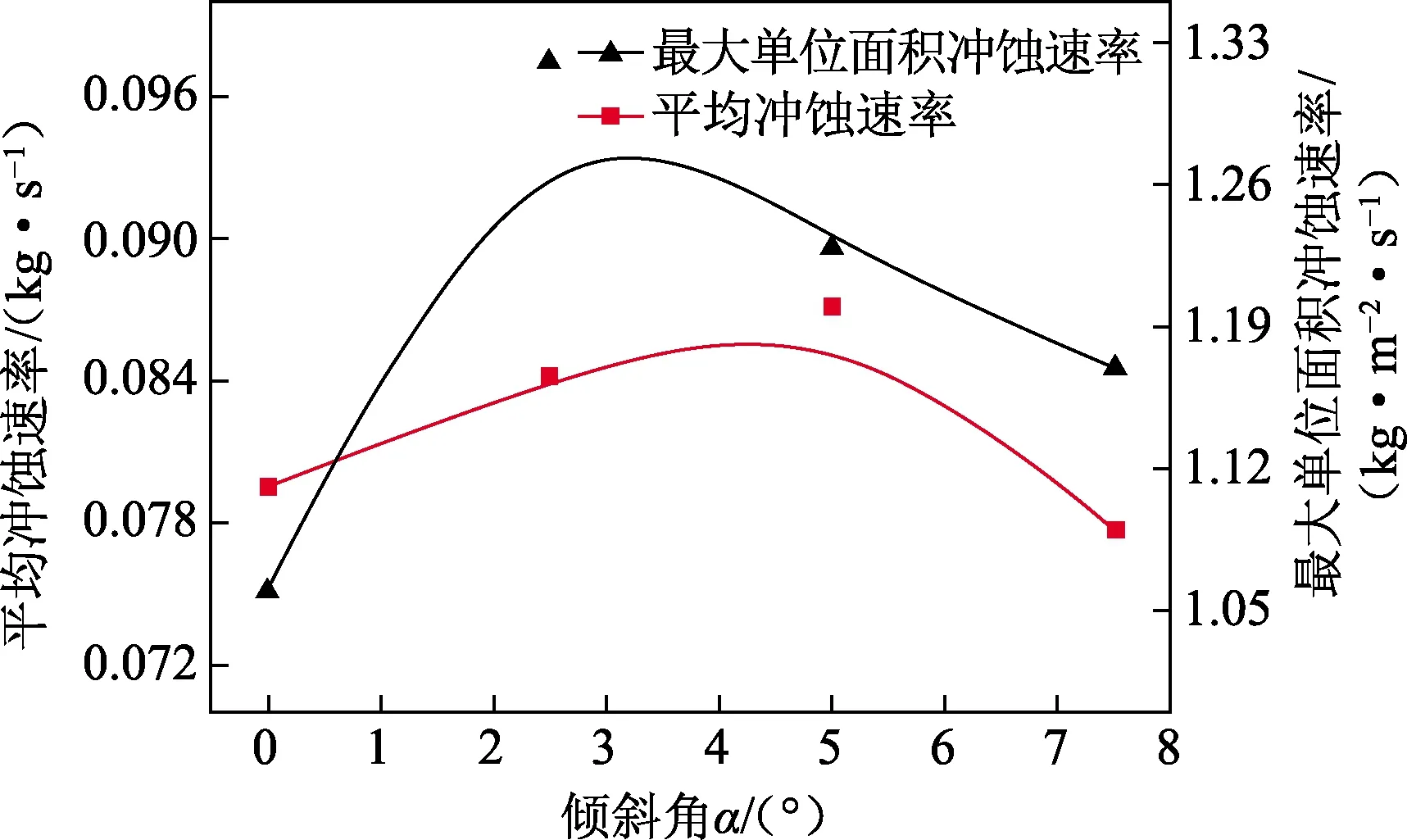
图8 平均冲蚀速率和最大单位面积冲蚀速率 随倾斜角的变化Fig.8 Average erosion rate and maximum unit erosion rate as a function of inclination angle

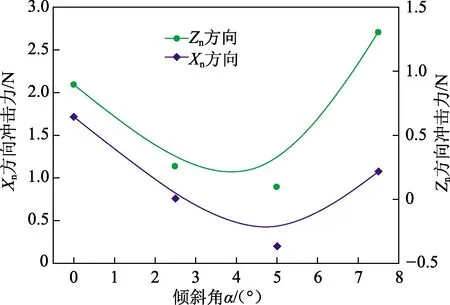
图9 粒子射流对井壁冲击力随喷嘴倾斜角的变化Fig.9 Impact force acted on the well wall as a function of inclination angle

粒子射流对井壁冲击力随喷嘴倾斜角的变化如图9所示。随着喷嘴倾斜角的增加,对井壁的冲击力先减小后增加。随着周向喷嘴角度增加,粒子射流以一定角度倾斜冲击水泥塞面,入射粒子射流和反弹粒子射流之间存在一定角度,相互之间的碰撞减弱[27],更利于粒子和水泥屑及时离开井底,因此对井壁的碰撞减弱。当倾斜角为5°时,对井壁冲击力最小,但是当倾斜角继续增加,反弹粒子倾斜角也增加,此时反弹粒子可能会直接冲击到井壁上,因此对井壁的冲击力增加。

3.4 喷 距

不同喷距下速度矢量剖面如图10所示。喷距为2～3cm时,粒子射流等速核能够作用到井底,而当喷距为4cm时,由于粒子射流运动距离的增加,射流等速核难以作用到井底(图10(c)),此时不利于粒子射流能量的充分利用;但当喷距为2cm时,井底漩涡区明显(图10(a)),井底流场运动复杂,易造成对井壁的高速冲击。

平均冲蚀率和最大单位面积冲蚀速率随喷距的变化如图11所示。随着喷距的增加,水泥塞的平均冲蚀速率和最大单位面积冲蚀速率均逐渐降低,随着喷距增加,粒子射流冲击到塞面的运动距离增加,由于流体阻力等原因,粒子射流在运动过程中能量损失增加[10,16],作用到水泥塞面的冲击能量减小,因此水泥塞的冲蚀速率减小。

图10 不同喷距下速度矢量剖面Fig.10 Velocity vector profile as a function of standoff distance

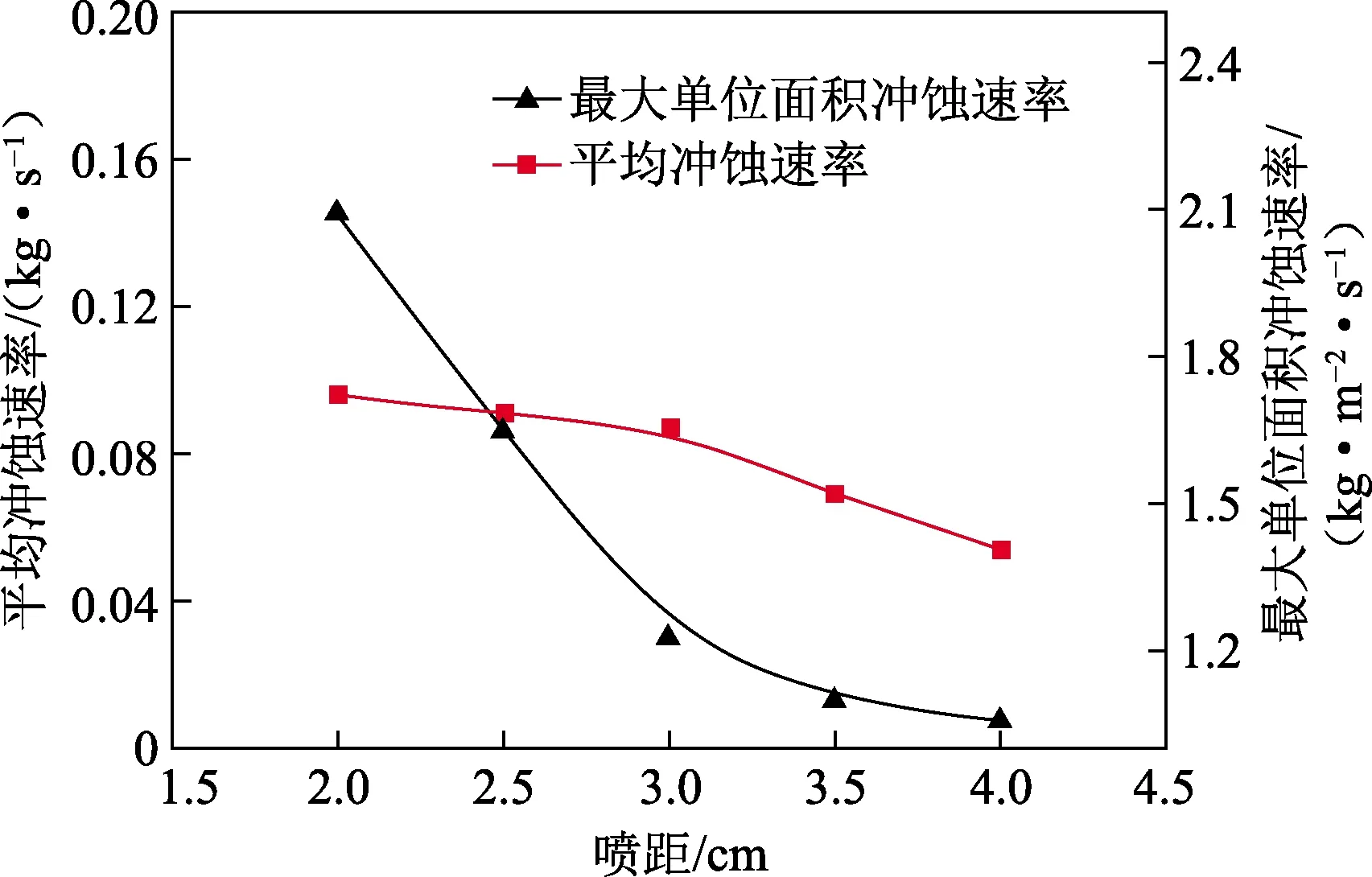
图11 平均冲蚀率和最大单位面积冲蚀速率 随喷距的变化Fig.11 Average erosion rate and maximum unit erosion rate as a function of standoff distance

粒子射流对井壁冲击力随喷距的变化如图12所示。随着喷距的增加,粒子射流对井壁的冲击力先减小后增加,喷距为3cm时对井壁的冲击力最小。喷距为2cm时,粒子射流运动至塞面距离较小,粒子射流以较高的速度冲击塞面,并以较高速度反弹,粒子射流漫流区的漫流速度较高,冲击到井壁上的粒子速度高,因此冲击力较高[28];喷距继续增加到4cm后,粒子射流运动距离增加,增大了粒子射流在井底运动空间,导致粒子射流在井底运动变得紊乱,加大了粒子冲击到井壁的几率,因此对井壁的冲击力增加。综合以上分析,喷距为3cm时钻塞效果较好。

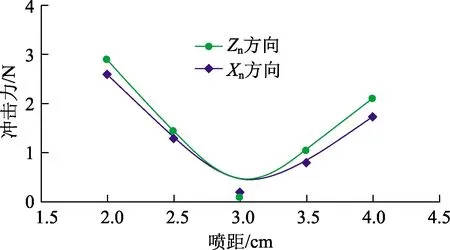
图12 粒子射流对井壁冲击力随喷距的变化Fig.12 Impact force acted on well wall as a function of standoff distance

4 全尺寸地面试验

开展139.7mm套管全尺寸粒子射流喷射钻塞地面试验。

4.1 试验设备

试验装置如图13所示。搅拌罐将石英砂粒与自来水搅拌均匀后,通过固井泵高压泵出,经高压管线输送至油管,从油管下部喷头喷出粒子射流,粒子以极高的速度冲击破碎水泥塞面,破碎的水泥屑经过上返环空、返出管线,存储到返出液罐中。其中水泥塞和上返环空外筒材质为有机玻璃,可直观清晰观测水泥塞钻进和上返情况。

图13 全尺寸粒子射流喷射钻塞地面试验装置Fig.13 Full scale ground test unit of drilling cement plug with particle waterjet

4.2 试验喷嘴

喷嘴结构和材质是影响粒子射流效率和钻塞工具寿命的关键。本研究喷嘴采用常用的圆弧-圆锥-圆柱三段式结构,喷嘴材质为YG6,如图14所示。

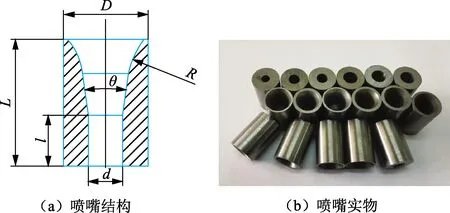
图14 硬质合金喷嘴Fig.14 Picture of carbide nozzles

4.3 试验材料及参数

水泥塞水灰质量比为44∶100;水泥塞外部为有机玻璃筒,外径为140mm,内径为121mm;水泥采用油田常用固井水泥;粒子为油田常用0.425～0.850mm石英砂。试验参数为泵压10MPa、排量500L/min、水泥塞长度1m、喷嘴压降7.5MPa、粒子喷速115m/s、喷嘴当量直径10.5mm、粒子体积分数5%。

4.4 结果分析

粒子射流钻塞地面试验如图15所示。试验过程中,粒子射流钻塞工具喷射高速粒子射流冲击水泥塞面,高效破碎水泥塞面,工具不断喷射钻进,破碎的水泥碎屑可在流体携带下顺利上返。

试验完水泥塞面实物如图16所示。可以看出粒子射流钻塞塞面平整,表明粒子射流可有效覆盖整个井底,实现了水泥塞的快速钻进。数值模拟时水泥塞平均冲蚀速率为0.087kg·s-1,地面试验冲蚀中30、60、90、120、150、180s对应的平均冲蚀速率分别为0.070、0.075、0.070、0.068、0.073和0.075kg·s-1。数值模拟与试验结果基本吻合,验证了数值模型的有效性,试验得到的冲蚀速率小于模拟冲蚀速率,是由于试验过程中实际粒子混合不均等条件和模拟条件不同导致的。

图15 粒子射流钻塞地面试验Fig.15 Ground test of drilling cement plug with particle waterjet

图16 试验完水泥塞面Fig.16 Cement plug surface after test

5 结 论

(1)粒子冲击破碎塞面后开始反弹,粒子速度明显降低,漫流区有利于钻屑及粒子及时离开井底并上返,而漩涡区不利于上返,易导致水泥屑重复破碎,井底最高压力分布在冲击区。

(2)喷嘴当量直径一定,水泥塞的平均冲蚀速率和最大单位面积冲蚀速率随周向喷嘴个数的增加先逐渐增加后减小,6个周向喷嘴时冲蚀速率最大,6～7个周向喷嘴时粒子射流能够均匀覆盖井底,对井壁的冲击力也较小;中心喷嘴消除了井底中心处的低速区,使中心漩涡也明显减弱,更利于粒子冲击能量有效利用和水泥屑及时离开井底,中心喷嘴使塞面冲蚀速率增加,对井壁冲击力减小。

(3)随着喷嘴倾斜角的增加,塞面平均冲蚀率先增加后减小,倾斜角为5°时,平均冲蚀率最大,对井壁冲击力最小,倾斜角为2.5°时最大单位面积冲蚀速率最大;随着喷距增加,水泥塞平均冲蚀速率和最大单位面积冲蚀速率均逐渐降低,对井壁的冲击力先减小后增加,喷距为3cm(约5倍喷嘴直径)钻塞效果较好。

(4)粒子射流可有效覆盖整个井底,实现了水泥塞的快速钻进,水泥碎屑可顺利上返;数值模拟与试验结果基本吻合,验证了数值模型的有效性。