基于反射振幅傅里叶系数的裂缝弱度反演方法

李 林， 张广智， 张佳佳， 李恒新， 郭彦民

(1.中国石油大学(华东)地球科学与技术学院,山东青岛 266580； 2.辽河油田勘探开发研究院，辽宁盘锦 124010)

“两宽一高”地震采集处理技术的发展，使得获取高品质“五维”(即空间三维坐标+炮检距+方位角)地震数据成为可能，如何充分挖掘五维地震数据中蕴藏的方位各向异性信息进行裂缝储层描述、流体识别和地应力预测逐渐成为研究热点[1-4]。发育有定向排列的高角度裂缝的储层在长波长假设条件下可等效为HTI介质，HTI介质中传播的地震波的物理性质表现出显著的方位各向异性。地震反射振幅随偏移距/入射角和方位角变化(AVOA/AVAZ)技术具有较高垂直分辨率，是进行裂缝检测的有效手段[5-7]。许多学者在推导HTI介质纵波反射系数方面作出了重要贡献[8-10]。法向和切向裂缝弱度是表征裂缝型储层特征的重要参数[11]。Shaw等[12]利用AVOA数据估算裂缝弱度和流体指示因子。陈怀震等[13-14]基于裂缝岩石物理模型先后开展了AVAZ反演和方位弹性阻抗反演。潘新朋等[15]研究了非均质HTI介质裂缝弱度参数地震散射反演方法。然而由于待反演参数较多，各向同性参数对反射系数的贡献远大于裂缝弱度参数对反射系数的贡献，且各参数之间通常存在耦合作用，这使得反演变得不稳定[16-17]。许多学者提出利用方位地震数据差异和方位弹性阻抗差异反演裂缝弱度[18-20]。Downton等[21-22]利用傅里叶系数重写方位纵波反射系数并实现了各向异性梯度估测。张繁昌等[23]探索了利用方位傅里叶反射系数预测正交介质裂缝密度的方法并进行了模型测试。笔者推导非均匀HTI介质纵波反射系数的傅里叶系数表达式，分析傅里叶系数对各向同性参数及裂缝弱度参数的敏感性，提出一种基于反射振幅傅里叶系数的裂缝弱度反演方法，通过分别进行各向同性参数反演和裂缝弱度参数反演来提高参数估计的准确性和鲁棒性。

1 纵波反射系数傅里叶系数表达式

在弱反射假设条件下，潘新朋等[15]基于Born近似和稳相法推导非均质各向异性HTI介质纵波反射系数方程如下：

RPP(φ,θ)=a(θ)RM+b(θ)Rμ+c(θ)Rρ+d(θ,φ)RΔN+

e(θ,φ)RΔT.

(1)

其中

e(θ,φ)=g0(sin2θcos2φ-sin2θtan2θsin2φcos2φ)，

式中，RPP(φ,θ)为HTI介质纵波反射系数;g0为上、下地层横波速度vS的均值平方与纵波速度vP的均值平方之比；RM、Rμ和Rρ分别为纵波模量、横波模量和密度的反射系数；RΔN和RΔT分别为界面上、下两侧地层的法向裂缝弱度反射系数和切向裂缝弱度反射系数；θ为入射角；φ为地震测线方位φ与裂缝对称轴方位φsym之间的夹角。

通过推导，方程(1)可以变为如下方程：

RPP(φ,θ)=r0(θ)+r2(θ)cos[2(φ-φsym)]+

r4(θ)cos[4(φ-φsym)].

(2)

其中rn(θ)(n=0,2,4)称为傅里叶系数，其与各向同性参数及裂缝弱度参数之间的关系为

r0(θ)=a(θ)RM+b(θ)Rμ+c(θ)Rρ+f(θ)RΔN+g(θ)RΔT,

(3)

r2(θ)=h(θ)RΔN+i(θ)RΔT,

(4)

r4(θ)=j(θ)RΔN+k(θ)RΔT.

(5)

其中

将方程(2)进一步展开，可得到由傅里叶系数正、余弦分量表征的纵波反射系数方程：

RPP(φ,θ)=a0(θ)+a2(θ)cos(2φ)+b2(θ)sin(2φ)+

a4(θ)cos(4φ)+b4(θ)sin(4φ).

(6)

式中，an(θ)和bn(θ)(n=0,2,4)分别为傅里叶系数余弦分量和正弦分量。

在某一固定入射角处，对于X个规则方位采样的情况，各阶傅里叶系数正、余弦分量可根据离散傅里叶变换得到：

(7)

(8)

式中，RPPk(φ,θ)为某一固定入射角处的第k个方位的反射系数；dφ为方位角的微分形式。各阶傅里叶系数正、余弦分量与各向同性参数及裂缝弱度参数之间的关系可通过推导方程(2)得到：

a0(θ)=a(θ)RM+b(θ)Rμ+c(θ)Rρ+f(θ)RΔN+g(θ)RΔT,

(9)

a2(θ)=h(θ)cos(2φsym)RΔN+i(θ)cos(2φsym)RΔT,

(10)

b2(θ)=h(θ)sin(2φsym)RΔN+i(θ)sin(2φsym)RΔT,

(11)

a4(θ)=j(θ)cos(4φsym)RΔN+k(θ)cos(4φsym)RΔT,

(12)

b4(θ)=j(θ)sin(4φsym)RΔN+k(θ)sin(4φsym)RΔT.

(13)

2 傅里叶系数敏感性

为了分析傅里叶系数对各参数的敏感性，设计双层模型，第一层为各向同性介质，第二层为HTI介质，模型参数设置如表1所示，其中法向弱度ΔN和切向弱度ΔT均为无量纲参数。

表1 模型参数Table 1 Model parameter

分别变化纵、横波模量反射系数、密度反射系数以及裂缝弱度反射系数，利用公式(3)～(5)分别计算各阶傅里叶系数，分析各阶傅里叶系数对纵、横波模量反射系数、密度反射系数以及裂缝弱度反射系数的敏感性。其中纵、横波模量反射系数、密度反射系数的变化范围为-0.2～0，裂缝弱度反射系数的变化范围为0～0.2，变化步长均为0.05。图1(a)～(e)分别为零阶傅里叶系数对纵、横波模量反射系数、密度反射系数以及裂缝弱度反射系数的敏感性，图2(a)～(b)分别为二阶傅里叶系数对裂缝弱度反射系数的敏感性，图3(a)～(b)分别为四阶傅里叶系数对裂缝弱度反射系数的敏感性。可以看出零阶傅里叶系数对纵、横波模量反射系数、密度反射系数的变化较为敏感，而对裂缝弱度反射系数的变化不敏感；二阶傅里叶系数对裂缝弱度反射系数的变化较为敏感；四阶傅里叶系数对裂缝弱度反射系数的变化不敏感。当入射角小于30°时，由于法向和切向裂缝对零阶傅里叶系数的贡献相对于纵、横波模量及密度对零阶傅里叶系数的贡献太小，可以忽略不计。因此可以将零阶傅里叶系数中的法向和切向裂缝弱度项省略，直接利用零阶傅里叶系数反演纵、横波模量及密度。由于法向和切向裂缝对四阶傅里叶系数的贡献远小于其对二阶傅里叶系数的贡献，且四阶傅里叶系数在地震数据含噪声情况下难以准确估测，因此后续仅利用二阶傅里叶系数反演裂缝弱度参数。

图1 零阶傅里叶系数r0(θ)对各参数的敏感性分析Fig.1 Sensitivity analysis of zero order Fourier coefficient r0(θ) to various parameters

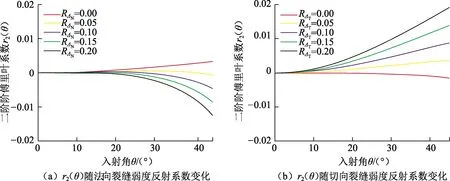
图2 二阶傅里叶系数r2(θ)对裂缝弱度反射系数敏感性分析Fig.2 Sensitivity analysis of the second order Fourier coefficient r2(θ) to fracture weakness reflectivity

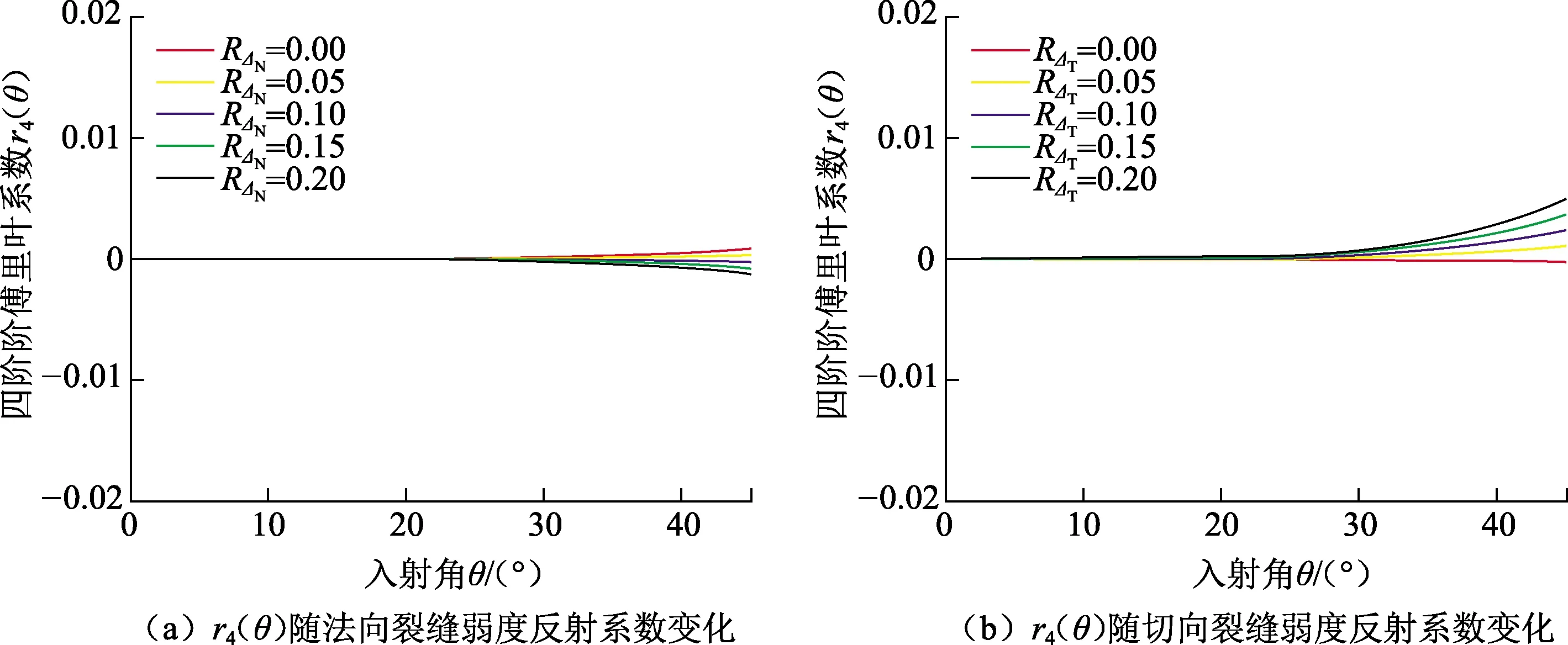
图3 四阶傅里叶系数r4(θ)对裂缝弱度反射系数敏感性分析Fig.3 Sensitivity analysis of the fourth order Fourier coefficient r4(θ) to fracture weakness reflectivity

3 反演流程

根据褶积定理，地震记录由地震子波和反射系数褶积得到：

S(φ,θ)=w(φ,θ)*RPP(φ,θ).

(14)

式中，S(φ,θ)为地震记录;w(φ,θ)为方位角度子波。在某一固定入射角处，对于X个规则方位采样的情况，含子波影响的各阶傅里叶系数正、余弦分量可根据离散傅里叶变换得到：

(15)

(16)

式中，An(θ)和Bn(θ)分别为包含有子波影响的傅里叶系数余弦分量和正弦分量；Sk(φ,θ)为某一固定入射角处的第k个方位的地震数据。

由于a0(θ)与零阶傅里叶系数表达式完全一致，而之前的分析表明当入射角小于30°时，零阶傅里叶系数r0(θ)对裂缝弱度反射系数的变化不敏感，因此可以将方程(9)中的裂缝弱度项省略，得到：

a0(θ)≈a(θ)RM+b(θ)Rμ+c(θ)Rρ.

(17)

方程(17)表明，利用零阶傅里叶系数可实现纵、横波模量及密度参数的反演。

对于纵、横波模量及密度的反演，假设时间采样点为N个，入射角为M个，根据方程(17)，并考虑到子波的影响，则可得如下矩阵表达式：

(18)

其中

a(θm)=diag[a1(θm),…,aN(θm)],

b(θm)=diag[b1(θm),…,bN(θm)],

c(θm)=diag[c1(θm),…,cN(θm)],

式中，diag表示对角矩阵；下标m表示第m个入射角；W(θm) 为角度子波矩阵。由于含子波影响的傅里叶系数仅与入射角有关，因此这里使用的子波仅为入射角的函数，而与方位角无关。

采用宗兆云等[24]提出的纵、横波模量及密度的贝叶斯线性化AVO反演方法，不同之处在于宗兆云等提出的方法的输入为AVO道集，而这里的输入为零阶傅里叶系数，在得到纵、横波模量反射系数及密度反射系数后，可利用道积分求取纵、横波模量及密度。

由于a2(θ)和b2(θ)分别为二阶傅里叶系数的余弦分量和正弦分量，而二阶傅里叶系数r2(θ)对裂缝弱度参数较为敏感，因此a2(θ)和b2(θ)对裂缝弱度参数也较为敏感。联立方程(10)和(11)，可利用二阶傅里叶系数正、余弦分量a2(θ)和b2(θ)反演裂缝弱度参数。AVAZ同步反演方法需输入X个方位和M个入射角下的地震数据，本文中提出的方法仅需输入M个入射角下的二阶正、余弦傅里叶系数，可减少数据占用内存空间，提高反演效率。

对于裂缝弱度参数的反演，联立方程(10)和(11)，并考虑到子波的影响，可得如下矩阵表达式：

d=Gm.

(19)

其中

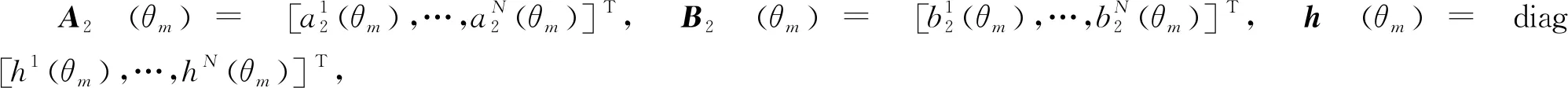
贝叶斯公式建立了模型参数后验概率分布与先验分布和似然函数间的量化关系，待反演模型参数的后验概率密度函数可表示为

(20)

其中似然函数p(d|m)描述了合成地震记录与观测地震记录差异的概率分布，假设似然函数p(d|m)服从均值为零的高斯分布：

(21)

根据实际情况的需要，先验分布可选择Huber分布、柯西(Cauchy)分布、高斯(Gauss)分布等[25]。研究表明，柯西分布为长尾分布函数，可以最大限度地提高垂直分辨率，保护弱小反射。假设模型参数先验概率分布p(m)服从柯西分布：

(22)

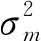
结合方程(20)～(22)，求解得到最大后验概率初始目标函数如下：

(23)

由于地震数据的带限性质，导致反演结果低频成分缺失或极不稳定[26]，因而需结合从裂缝岩石物理建模估测得到裂缝弱度低频信息，得到最终的反演目标函数：

(24)

式中，λΔN和λΔT分别为法向和切向裂缝弱度的加权系数；ΔN0和ΔT0为法向和切向裂缝弱度的初始模型，可以通过各向异性裂缝岩石物理模型的估算结果得到[27]；P为下三角积分矩阵。利用迭代重加权最小二乘法求解方程(24)以估测法向和切向裂缝弱度反射系数，然后利用积分求得法向和切向裂缝弱度：

ΔN=PRΔN.

(25)

ΔT=PRΔT.

(26)

4 模型测试

利用单口井数据进行模型试算，以验证所提出方法的可行性和稳定性。井数据中包括纵、横波模量、密度曲线及通过各向异性裂缝岩石物理建模估测得到的法向和切向裂缝弱度曲线。选取主频为35 Hz的雷克子波，利用测井数据结合方程(1)合成4个方位(0°、45°、90°和135°)下的地震记录，并向合成地震记录中分别添加信噪比为5和2的随机噪声，以验证该方法的抗噪性和稳定性。无噪声和含不同噪声的合成地震记录见图4。相应的反演结果见图5。可以看出无噪声情况下反演结果与真实模型基本一致；信噪比为5和2情况下的反演结果与真实值趋势大体相同，验证了所提方法的抗噪性和稳定性。

图4 无噪声和含不同噪声情况下的合成地震记录Fig.4 Synthetic seismic data without noise and with different noise levels

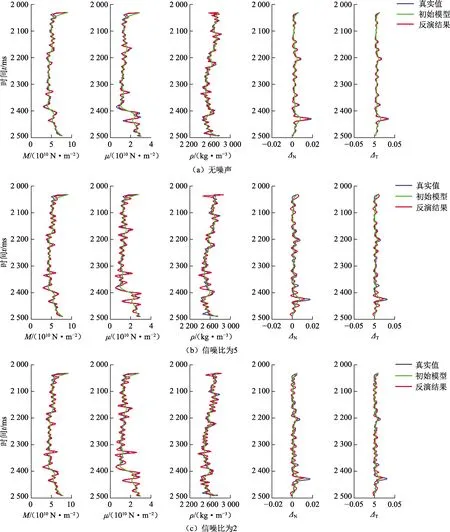
图5 不同信噪比情况下的反演结果Fig.5 Inversion results for synthetic data with different signal-to-noise ratios

5 实际资料试处理

实际资料来自于中国西南某研究区，目的层段砂体厚度大，分布范围广，储层物性差，孔隙度多小于5%，渗透率主峰位多小于0.1×10-3μm2。气藏埋藏深度大，地层压力高，而且单井产能差异大，主要受裂缝控制，裂缝发育程度主要与断层相关。方位叠前地震数据已事先经过去噪保幅等处理。考虑到地震数据的偏移距和方位分布及信噪比的影响，将方位叠前地震数据划分为4个方位，分别为22.5°(0°～45°)、67.5°(45°～90°)、112.5°(90°～135°)和157.5°(135°～180°)，入射角划分为3个，分别为小角度18°(15°～21°)、中角度22°(19°～25°)和大角度26°(23°～29°)，共得到12个方位部分角度叠加地震剖面(图6)。首先利用方位部分角度叠加地震数据提取零阶和二阶傅里叶系数正、余弦分量，然后利用零阶傅里叶系数反演得到纵、横波模量及密度，利用二阶傅里叶系数正、余弦分量反演得到法向和切向裂缝弱度，相应的反演结果见图7和8，同时在反演结果剖面中绘制了相应的井曲线。可以看出纵、横波模量、密度及法向和切向裂缝弱度的反演结果与测井曲线较为吻合，且反演剖面呈现出较好的连续性。图6中标注的白色椭圆表示裂缝发育区域，该区域的法向和切向裂缝弱度反演结果呈现出高值，有助于识别裂缝发育的横向展布情况。

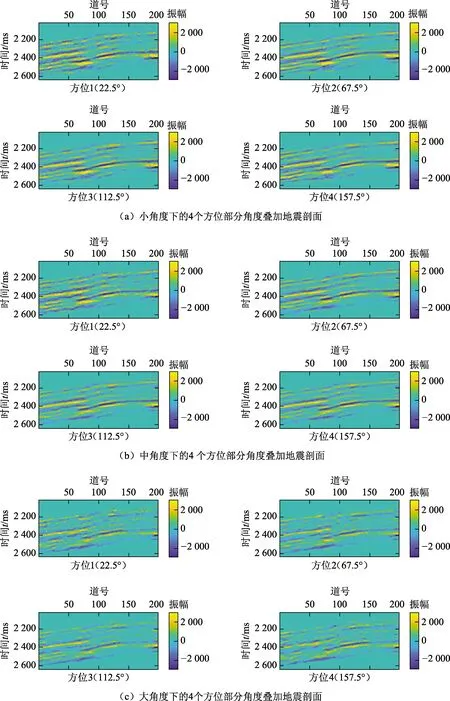
图6 方位部分角度叠加地震剖面Fig.6 Azimuthal angle stack profiles

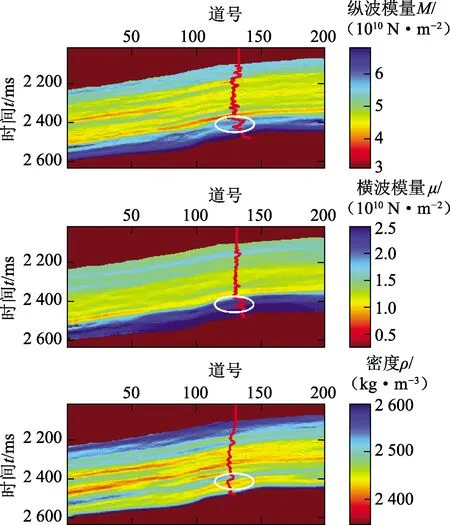
图7 纵、横波模量、密度反演剖面Fig.7 Inverted P-wave modulus, S-wave modulus and density profiles

图8 法向和切向裂缝弱度反演剖面Fig.8 Inverted normal and tangential fracture weakness profiles

6 结束语

首先推导了非均匀HTI介质纵波反射系数的傅里叶系数表达式，利用傅里叶级数分解方法分别进行各向同性参数反演和裂缝弱度参数反演，零阶傅里叶系数对各向同性参数变化较敏感，可用于反演各向同性参数，而二阶傅里叶系数对裂缝弱度参数变化较敏感，可用于反演裂缝弱度参数。利用该方法可提高裂缝弱度参数估计的准确性和鲁棒性，模型测试和实际应用结果证明了该方法的稳定性和有效性。此外，不同于常规AVAZ同步反演需输入不同方位不同入射角下的地震数据，提出的新方法只需输入不同入射角下的二阶傅里叶系数正、余弦分量，可有效地减少数据占用存储空间，提高裂缝弱度参数反演的效率。