时变子波提取及其在地震资料智能处理中的应用

戴永寿, 张 鹏, 万 勇, 孙伟峰, 张彧豪, 韩浩宇, 吴莎莎

(1.中国石油大学(华东)海洋与空间信息学院,山东青岛 266580; 2.中国石油大学(华东)控制科学与工程学院,山东青岛 266580)

近年来,中国在塔里木盆地库车等地区发现了具有相当规模的油气藏资源,但主体目的层位于深层或超深层,且地表地形起伏大、地下构造异常复杂,导致反射信号能量弱、地震资料品质差、成像精度低[1]。常规地震数据处理方法已无法满足新形势下高分辨率地震勘探的需求[2-3],亟需融合智能信息处理新技术为深层油气藏的勘探与开发提供新思路。地震子波是影响地震资料分辨率的关键因素,也是地震正反演、速度建模和偏移成像的重要基础。早期研究通常假设地震子波时不变,但该假设仅适用于中浅层及简单构造资料的处理;而对于深层复杂构造,地层的吸收与频散作用导致子波在传播过程中出现高频衰减和相位畸变,因此具有时变性[4]。时变地震子波的准确提取对于提高地震资料处理和解释精度具有重要的意义。笔者将采用智能信息处理技术通过分别估计振幅谱与相位谱提取时变地震子波,并应用于反褶积、偏移等地震数据处理主要环节,提出基于稀疏表示的叠后非平稳反褶积方法以及利用时变子波提高叠前偏移成像精度的方法。

1 时变子波提取方法

非平稳褶积模型[5]可表示为

x(t)=w(t,τ)*r(t)+n(t).

(1)

式中,x(t)为非平稳地震记录;w(t,τ)为时变子波;r(t)为反射系数序列;n(t)为噪声干扰,实际资料中既包含高斯噪声,也包含非高斯噪声。采用改进的广义S变换[6]对式(1)进行时频变换和滤波处理,则x(t)、w(t,τ)和r(t)在时频域的关系可以表示为

X(t,f)=W(t,f)·R(t,f).

(2)

式中，X(t,f) 、W(t,f)和R(t,f)分别为地震记录、时变子波和反射系数序列的时频谱。

再对等式两边进行对数变换,则地震记录、子波和反射系数的对数谱之间的关系如下:

ln|X(t,f)|=ln|W(t,f)|+ln|R(t,f)|.

(3)

式中,ln|R(t,f)|为高频信号,具有振荡剧烈的特点;ln|W(t,f)|为低频信号,具有光滑连续的特点。因此时变子波振幅谱的提取问题即可转化为信号去噪问题。互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)是目前应用效果最好的智能去噪方法[7],本文中利用CEEMD将不同时刻地震记录的对数振幅谱分解为一组具有不同振荡尺度的分量,滤除振荡剧烈分量,重构光滑连续分量,即实现了时变子波振幅谱的准确提取。

在子波振幅谱提取的基础上,研究采用智能寻优方法提取时变子波相位谱。对子波振幅谱进行希尔伯特变换即可估计时变最小相位子波[8]。应用极零点模型描述最小相位子波Z域的系统函数:

(4)

式中,a、b为待估计的参数;m、n为模型的阶次。针对式(4)所示的线性差分系统,采用递推最小二乘法辨识模型中的参数,然后令分子和分母分别等于零,能够估计得到最小相位子波Z域的极零点;再根据不同相位特征的子波极零点分布的规律及差异,对最小相位子波的极零点关于单位圆进行对称变换,并在局部相似度准则的约束下确定最优的组合,实现时变混合相位子波的准确提取[9]。具体实现流程如下:

(1) 计算地震记录的包络。

(2) 利用不同极零点组合所对应的子波相位谱对地震记录进行相位校正。

(3) 分别计算相位校正后地震记录的局部包络h(t)与原地震记录的局部包络s(t)的相似系数。计算公式为

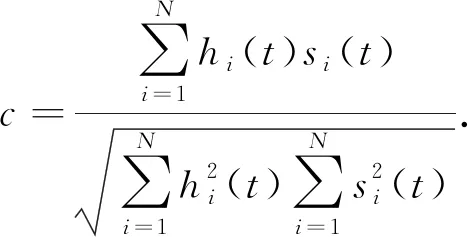
(5)

式中，c为相似系数。

(4) 当相似系数的倒数取最大时,对应的极零点分布为最优组合,对应的子波即为最优的时变子波。

2 叠后非平稳反褶积

反褶积是压缩地震子波、提高地震资料分辨率最为直接有效的处理技术。叠后水平层状介质中的反射系数序列具有稀疏性,而人工智能领域的稀疏表示理论与方法正是解决稀疏反演问题的有效手段。

式(1)的矩阵形式可以表示为

x=Wr+n.

(6)

式中，x为地震记录向量;W为时变子波矩阵;r为反射系数序列向量;n为噪声向量。

针对现有方法难以在高斯与非高斯噪声共同干扰下准确反演反射系数序列的问题,利用L2范数能够压制高斯噪声、L1范数对非高斯噪声具有较好抑制能力的特性,建立混合范数约束的反演目标函数[10]:

(7)

式中,μ为正则化参数;λ1和λ2为权重系数,用来调节L1和L2范数约束的拟合误差项的权值,取值范围为[0, 1],且λ1+λ2=1。分裂Bregman迭代是对包含L1范数约束项的目标函数进行最小化求解最为快速有效的算法,其主要思想是利用中间变量将L1范数约束中的表达式分离出来,从而将单变量单目标函数分裂为多变量多目标函数的交替迭代,使其更容易求解。令d1=Wr-x,d2=r,反演目标函数[11]可以分裂为

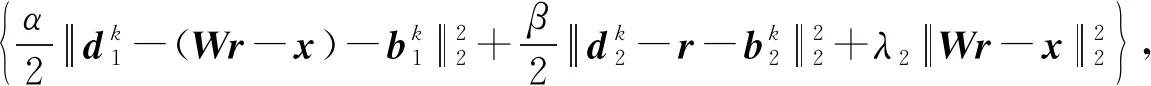
(8)

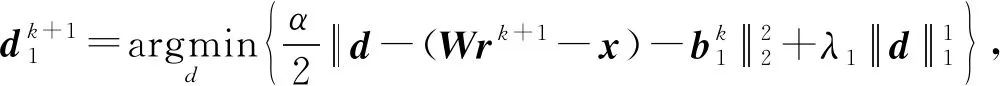
(9)

(10)

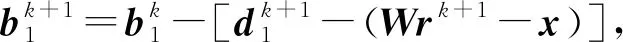
(11)

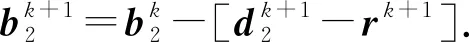
(12)

对式(8)直接求导,再令导数等于0,即可估计每次迭代中的反射系数序列

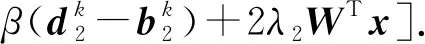
(13)

式(9)和(10)均满足邻近算子的定义式[11-12],可分别改写为

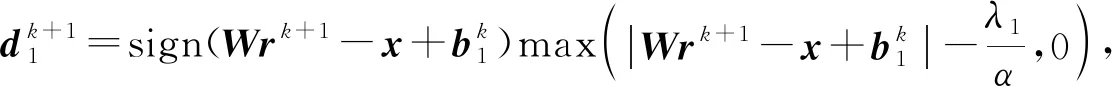
(14)

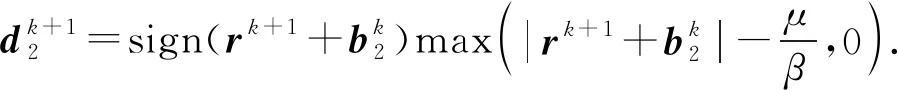
(15)

式中,sign(y)为符号函数,y>0时取值为1,反之取值为-1。综上所述,利用式(13)～(15)、(11)和(12)的交替迭代即可在高斯与非高斯噪声共同干扰下实现反射系数序列的准确反演。

3 叠前偏移成像方法

叠前资料的偏移成像方法由于包含丰富的波形信息近年来得到广泛关注,而震源子波的估计精度不佳以及地震记录频带较窄是影响偏移成像效果的主要因素[13]。理想的震源子波为尖脉冲,但实际上震源子波为能量集中在前端、具有一定延续长度的波形,符合最小相位特征[11]。对于叠前炮数据,零偏移距地震道是最先接收到地震波的地震记录,则该道地震记录中初始时刻的子波最接近震源子波。因此本文中首先从零偏移距地震记录中提取时变子波,然后对初始时刻的子波振幅谱进行希尔伯特变换即可实现具有最小相位特征的震源子波估计。

由于叠前地震资料具有低信噪比、强衰减的特点,地震资料高低频缺失严重、频带较窄,直接对叠前资料进行偏移会导致虚假成像和模糊成像,不能准确反映地下构造真实的位置和形态,进而影响后续处理和解释精度。本文中采用反Q滤波结合维纳反褶积的方法对叠前地震资料进行拓频处理。地层品质因子Q是描述介质的非完全弹性特征,表征地层吸收衰减的重要参数。研究者们先后提出了多种Q值估计方法,其中频率域的谱比法是最常用且效果最好的方法[14]:

(16)

式中，A(t0,f)和A(t1,f)为不同时刻提取的子波振幅谱。式(16)是关于f的线性函数,其斜率为-2π(t1-t0)/Q。对不同时刻提取的子波振幅谱A(t0,f)和A(t1,f)作差并在有效频带内进行线性拟合求得斜率后,即可估计得到品质因子Q[15]。在Q值估计的基础上,利用下列公式可实现对地震资料的反Q滤波处理[16]:

XQ(t,f)=X(t,f)Λ(t,f),

(17)

Λ(t,f)=[β(t,f)+σ2]/[β2(t,f)+σ2],

(18)

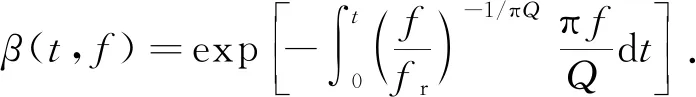
(19)

式中,X(t,f)和XQ(t,f)分别为反Q滤波处理前后地震记录的时频谱;β(t,f)为滤波因子;σ2为稳定因子;fr为参考频率;Λ(t,f)为振幅补偿因子。反Q滤波能够对叠前资料中的高频衰减进行有效补偿,使得深层部分的能量得到提升。完成反Q滤波处理后,继续对地震资料进行维纳反褶积[17]:

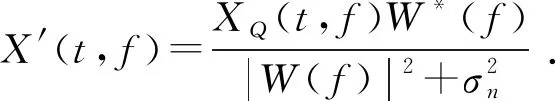
(20)

4 数值仿真验证

为了验证时变子波提取方法的有效性,本文中采用ARMA模型描述原始子波,并利用下式构造时变子波[21]:

w(t,τ)=

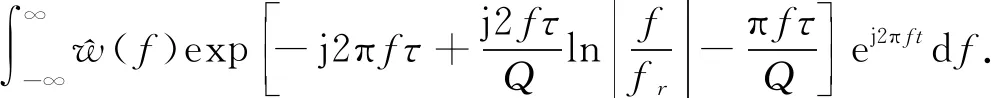
(21)

图1 合成地震记录Fig.1 Synthetic seismogram

采用振幅谱与相位谱分别估计的时变子波提取方法从图1(c)中估计不同时刻的子波,结果如图2所示,图2(a)～(d)分别为111、381、619及892 ms的提取结果。

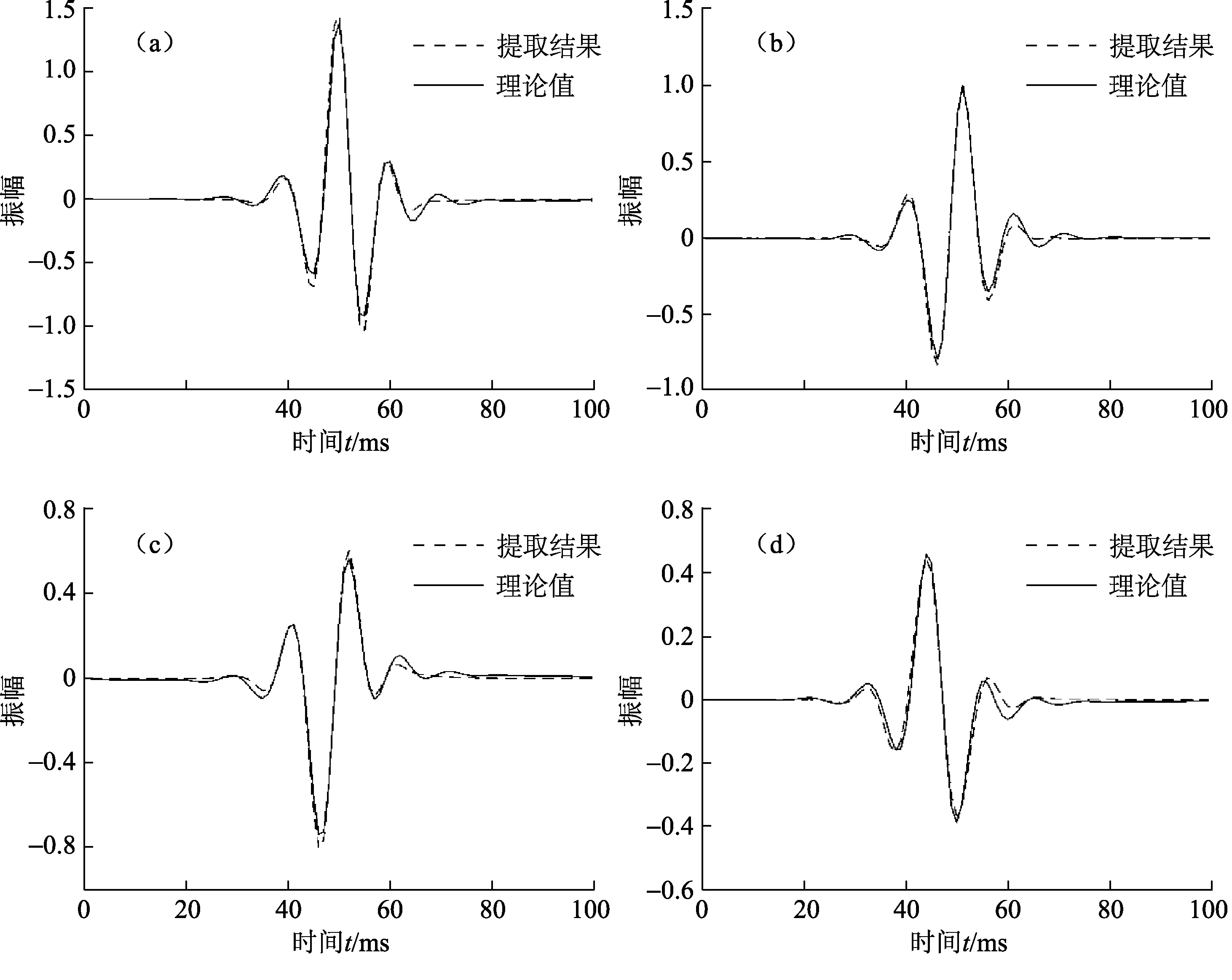
图2 时变地震子波提取结果Fig.2 Time-varying wavelet extraction results

从图2中可以看出本文方法能够准确提取不同时刻的子波,且能真实反映动态衰减特征。利用提取的子波对图1(c)进行反褶积处理,应用基于稀疏表示的非平稳反褶积方法反演反射系数序列,结果如图3所示,在一定强度的高斯与非高斯噪声共同干扰下,本文方法也能有效压缩地震子波,较为准确地估计反射系数序列。

图3 反射系数序列反演结果Fig.3 Results of reflection coefficient inversion

震源子波估计不准及地震资料频带较窄是造成叠前偏移成像效果不佳的主要原因。本文中通过正演模拟合成40炮记录,每炮记录包括901道,采样点3 750个,以第20炮为例(图5(a))。首先采用本文方法从零偏移距地震道(图5第401道)中估计不同时刻的子波,然后对初始时刻子波的振幅谱进行希尔伯特变换,实现震源子波估计。基于式(16)进行品质因子Q值估计,并利用式(17)～(19)对地震资料进行反Q滤波处理,以补偿地层衰减。再采用式(20)对地震资料进行维纳反褶积,以压缩子波、拓宽地震记录频带。从图4可以看出利用本文方法能够准确提取震源子波,有效解决震源子波估计的难题。

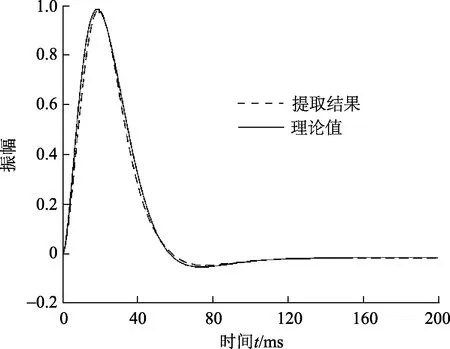
图4 震源子波估计结果Fig.4 Estimation of source wavelet

图5 模拟单炮记录Fig.5 Simulated single shot record

图5表明利用提取的子波进行拓频处理后地震资料的深层能量得到了提升,边界更加清晰。最后应用最小二乘逆时偏移方法对地震资料进行成像,结果如图6所示。对比图6(a)和(b)可以看出,在不经过处理的情况下直接进行偏移成像,地下构造出现了虚假的双重边界,而利用本文方法估计震源子波并实现高频延拓,再进行偏移处理能够有效提高成像精度。

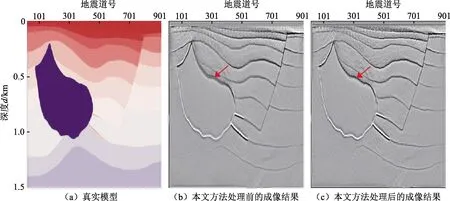
图6 偏移成像结果Fig.6 Migration imaging results

5 实际资料处理

为了验证基于时变子波的地震资料智能处理技术在实际地震数据处理方面的有效性,首先选取胜利油田某区块叠后地震剖面(图7(a))并提取时变地震子波,然后利用分裂Bregman迭代法对地震剖面进行反褶积处理,结果如图7(b)所示。对比图7(a)和(b)可以得出,经本文方法处理后叠后地震剖面的分辨率更高,同相轴更细,能够为地震资料的解释提供重要的参考。图8为图7反褶积结果的频谱,从中可以看出经处理后地震资料的频带宽度得到了明显的提升。

图7 实际叠后地震资料反褶积结果Fig.7 Deconvolution result of actual poststack seismic data

图8 反褶积前后频谱的对比Fig.8 Comparison of average normalized amplitude spectra of images shown

为了进一步验证本文方法在叠前偏移成像中的重要作用,从图9(a)所示叠前炮数据中估计震源子波,再利用反Q滤波与维纳反褶积相结合的方法对地震资料进行拓频处理,结果如图9(b)所示。可以看出，深层能量得到了有效补偿,同相轴更细。在此基础上应用最小二乘逆时偏移方法进行成像,结果如图10所示。

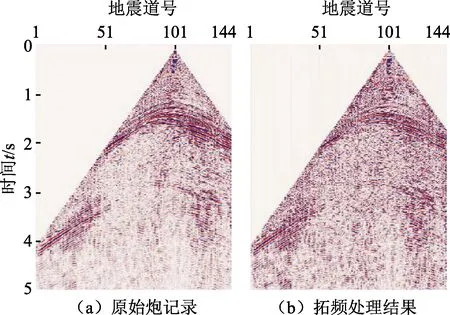
图9 叠前炮数据的拓频处理Fig.9 Frequency expanding of prestack seismic data

图10 叠前地震资料的偏移成像结果Fig.10 Migration imaging results of prestack seismic data

从椭圆标记处可以看出经处理后的成像结果所受的干扰更少,对层位的反映更清晰。将虚线框标记的区域进行放大,表明本文方法能够使同相轴连续性更好,振幅能量更均衡。

6 结束语

初步探究了时变子波提取及其在地震资料智能处理中的应用。利用智能信息处理技术通过分别估计不同时刻子波的振幅谱和相位谱实现了时变地震子波提取;提出了基于稀疏表示的叠后非平稳反褶积方法,在复杂噪声干扰下反演反射系数序列,提高地震资料的分辨率;研究了时变子波在叠前偏移中的应用方法,通过震源子波估计与地震记录的拓频处理,进一步提高了成像精度。今后将继续研究利用随机共振方法的低信噪比地震资料无损降噪技术、基于卷积神经网络的叠前子波提取方法以及基于压缩感知的地震数据低频补偿方法,最终有效应用于塔里木深层地震资料的处理,实现高精度全波形反演与偏移成像。