石墨烯薄膜与半导体界面热输运规律

2020-12-24徐伟华王照亮

中国石油大学学报（自然科学版） 2020年6期

刘明, 徐伟华, 许康, 王照亮

(1.中国石化胜利油田分公司石油工程技术研究院,山东省稠油开采技术重点实验室,山东东营 257000; 2.中国石油大学(华东)新能源学院,山东青岛 266580)

随着电子器件的集成化程度不断提高,其特征长度接近甚至达到纳米量级。纳米设备的行为和可靠性强烈依赖于散热方式。微/纳米尺度的电子设备将不可避免地带来热稳定性问题,进而导致设备损坏[1-2]。石墨烯具有比炭黑和碳纳米管更大的比表面积[3],其电荷载流子表现出巨大的本征迁移率,有效质量为零,在室温下可以传播几微米的距离而不被散射[4]。由于石墨烯的优异性能,其在电子器件热管理应用材料方面具有极大潜力。当把石墨烯集成到电子器件内部时,石墨烯会与其他的材料之间产生许多的界面,此时影响热输运过程的是界面热阻。Alvarez等[5]用3ω方法测量在30～300 K范围内,厚度为20～150 nm的非晶Ge薄膜的热导率。并观察到随着薄膜厚度减小,膜的有效热导率降低。Yu等[6]采用经典的非平衡分子动力学模拟研究石墨烯-硅界面的界面热阻。Diao等[7]用分子动力学计算了在不同压力下,碳纳米管和硅的界面热导。在受到压力时,不论是封口的还是不封口的碳纳米管,界面热导都会增大。Zhan等[8]研究了Si/Ge界面热阻与温度的关系,界面热阻随温度的升高而降低。Fan等[9]利用分子动力学模拟研究功能化的单壁碳纳米管和硅之间的界面热导,随着碳纳米管和硅表面的成键数增加,界面热导增加。对于现在广泛使用的半导体材料(硅、氮化镓与石墨烯)的界面传热研究有欠缺。笔者从石墨烯与硅和氮化镓的界面热输运出发,研究石墨烯与硅、石墨烯与氮化镓界面间的传热规律;同时考虑器件工作温度、石墨烯层数对界面热导的影响;并从声子态密度和声子能量层面对引起界面热导变化的原因进行分析。

1 理论基础

界面热阻也叫Kapitza热阻,定义为界面温差与通过界面的热流密度的比值,界面热阻的倒数为界面热导。

RBD=ΔT/Q或G=Q/ΔT.

(1)

式中,Q为界面的热流密度,eV/(ps·Å2);RBD为界面热阻,m2·K/W;ΔT为界面温差,K;G为界面热导,W/(m2·K)。

在分子动力学模拟中通过牛顿运动方程描述粒子运动,通过将系统的微观粒子(原子或分子)视为宏观粒子,建立分子的牛顿运动方程;通过求解所有粒子的运动方程,记录各个时刻的粒子动量等信息;最后根据统计理论,得到温度、压力等各种宏观信息。势函数用来描述粒子间的相互作用,势函数的选取直接决定粒子间的作用力,因此势函数的选取至关重要。描述分子间作用力的势函数有很多,主要分为対势和多体势,常用的对势是Lennard-Jones势,表示为

(2)

式中,εij为力的强度,eV;σij为原子的平衡间距,Å。

Lennard-Jones势适合于惰性气体和简单液体的分子相互作用。常用的多体势函数有EAM势、Stillinger-Weber(SW)势、Tersoff势、Airebo势,所以计算过程中对于不同的材料及性质应选取适合的势函数。

根据对北部湾经济区区域一体化现状的定量分析结果可以看出，当前全区区域经济发展滞后的影响因素确实存在，主要包括以下几类问题：市场、贸易、产业、城乡结合方面发展不合理。市场方面的问题主要集中在市场的分割、市场无序发展、恶性竞争等等，贸易方面的问题主要集中在区内区域间的贸易壁垒、贸易失衡等等，产业方面的问题主要集中在产业结构不合理、新型产业发展受到阻碍等等。城乡结合方面的问题主要集中在城乡发展不均衡，城市分工不明确等等。另外，其他一些客观因素也阻碍了北部湾经济区区域经济的发展。

2 石墨烯薄膜与硅的界面热输运

2.1 物理模型

用Materials Studio构建模型,为了保证晶胞的完整性以及确保统计的准确性,模型两侧选用6×6×10个硅晶胞所组成的硅基体,截面积为32.58 Å×32.58 Å,共计5 760个硅原子;中间是31.84 Å×31.84 Å的石墨烯片,共363个碳原子。此外,在周期性边界条件下,该模型中石墨烯与其镜像之间由C—C键连接,统计面积尺寸时,以原子位置为基准,并未考虑键的位置;在此尺寸搭配下,可以避免出现空穴,晶格的失配对于结果的影响可以忽略不计。

2.2 模拟过程

采用LAMMPS并行软件包模拟,用NEMD研究界面热输运问题。在x和y方向均采用周期性边界条件。石墨烯中的碳原子间相互作用选用AIREBO势[10-11];硅基体中原子间作用选用Tersoff势[12];而硅和碳之间的作用,只考虑范德华力,选用Lennard-Jones势能,其中取εC-Si=0.008 909 eV,σC-Si=3.326 Å[6]。

模拟首先采用NVT系综,运行1×106步,使系统达到设置的初始温度,然后再在NVE系综下运行,时间步长取为0.25 fs。把模型沿z方向分成20层,将每层温度输出,便可得到温度分布。在模拟过程中,为了避免产生能量漂移,提高计算效率,选用改进的非对称热交换算法,设定热流为3.0 eV/ps。由于分子动力学模拟具有随机性,模拟次数较少不能准确说明问题;对于同一种条件需要多次模拟求平均才可具备一定的可信度,所以模拟过程的随机性将会导致一定的不确定度。为了减小模拟的随机性对结果的影响,在计算各参量时均模拟8次。

2.3 模拟结果

图1为系统的温度分布。从图1中可以看出,在中间位置有一个明显的温差,因此中间存在界面的区域有一个较大的温降,这是因为存在界面热阻。由于所施加的热流Q已知,再将界面处的温降记录下来,即可以求得石墨烯片和硅基体之间的界面热导。

图1 系统温度为300 K时的温度分布Fig.1 Temperature distribution when system temperature being 300 K

2.3.1 界面热导的温度效应

图2为界面热导与温度的关系。由图2可知,温度越高,石墨烯与硅基体的界面热导越大。这是由于随着温度升高,声子的非弹性散射增强,声子的透射系数增加,从而导致界面热导增加。

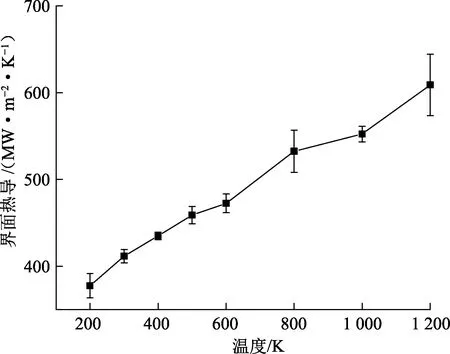
图2 硅和石墨烯之间的界面热导随温度变化Fig.2 Temperature dependence of thermal conductivity at interface between silicon and graphene

图3为不同温度下界面处的碳原子和硅原子的声子态密度曲线。由图3可以看出,界面处的硅原子的截止频率约为20 THz,而碳原子的截止频率为60 THz。VDOS的匹配程度是产生界面声子散射的主要机制,在5 THz时,随着温度升高,硅原子的声子态密度降低,从而增大了硅原子和碳原子的耦合程度,从而使得界面热导增加。而在频率大于20 THz时,由于硅原子的态密度为零,即使碳原子的态密度较大,对界面热导的影响也很小。

将硅原子和碳原子之间的态密度曲线的耦合程度进行量化[13-14],表示为

(3)

式中,E为VDOS重叠区域的声子能量,eV;h为普朗克常数,eV·s;ν为振动频率,Hz;T为系统温度,K;ωc为截止频率,Hz;g0(ν)为重叠区域的VDOS。

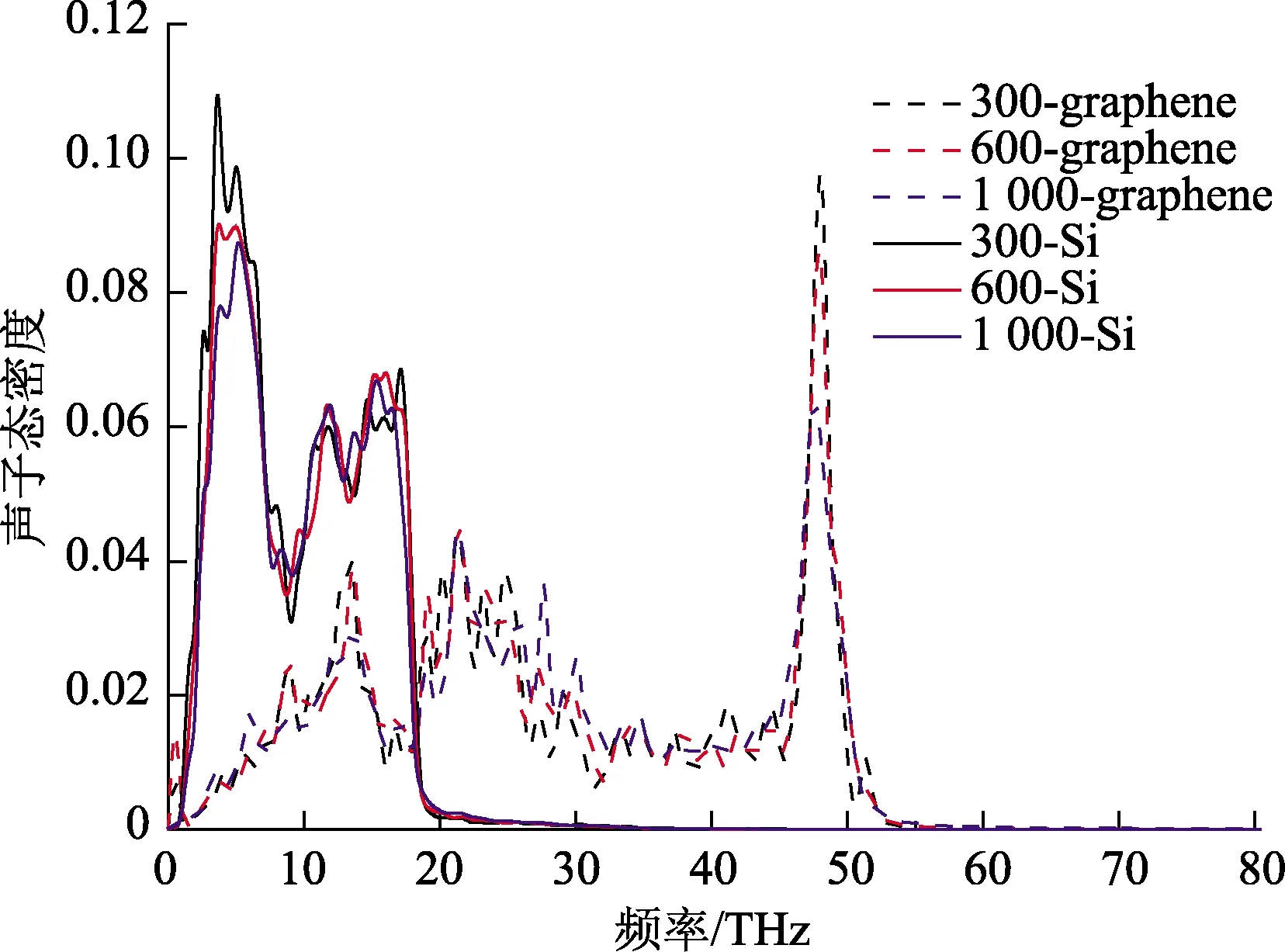
图3 温度为300、600和1 000 K时界面处的C和Si的声子态密度曲线Fig.3 Vibration density of states of C and Si at interface when temperature being 300、 600 and 1 000 K

图4为碳原子和硅原子VDOS重叠区域的声子能量。从图4中可以看出,VDOS重叠区域的声子能量随温度的变化与界面热导随温度的变化趋势一致。

图4 不同温度下Si和C的声子态密度重叠区域的声子能量Fig.4 Overlapped phonon energy of VDOS between Si and C at different temperature

2.3.2 石墨烯层数对界面热导影响

图5为不同层数的石墨烯与硅之间的界面热导,为了更好地反映器件在室温条件下工作的情况,将模拟的环境温度设定为300 K。从图5中可以看出,随着石墨烯层数增加,界面热导降低,并且从一层增加到两层时,有明显的降低,而后界面变化不大。这是由于多层石墨烯层间的粒子会与声子发生碰撞,从而导致声子散射,因此穿过界面的声子会减小,从而使得界面热导降低。而随着石墨烯层数增加,其性质接近于石墨,此时界面热导也不再变化。

图5 不同石墨烯层数下硅基体和石墨烯之间的界面热导Fig.5 Interfacial thermal conductivity between silicon and graphene with different graphene layers

在不同石墨烯层数下,界面处的碳原子和硅原子的声子态密度曲线如图6所示。从图6中可以看出,当石墨烯层数为二、三、四层时,碳原子和硅原子的态密度变化不大;而当石墨烯为单层时,硅原子的截止频率有所增大,并且在5 和15 THz时,硅原子的态密度较多层石墨烯的降低;在13 THz时,碳原子的态密度比多层石墨烯的有所增大,这些情况都增大了碳原子和硅原子的声子态密度重叠区域振动模式,从而使得碳原子和硅原子声子谱的匹配程度大大提高,这都利于界面热传导。即单层石墨烯情况下,界面热导较大。

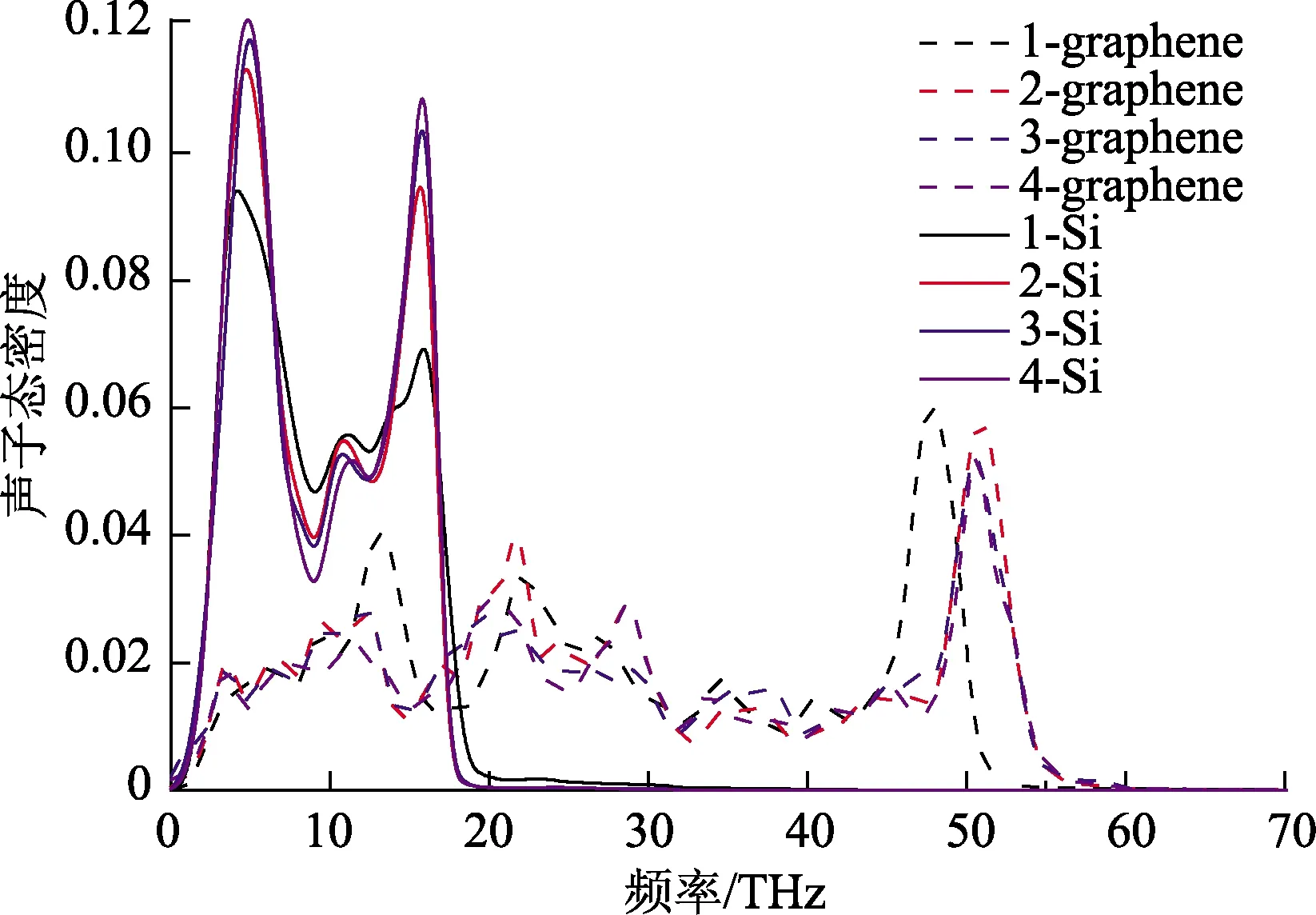
图6 石墨烯层数为1～4时界面处的C和Si的声子态密度曲线Fig.6 VDOS of C and Si at interface when layers of graphene being 1～4

3 石墨烯薄膜与氮化镓的界面热输运

3.1 物理模型

用MS构建模型,为了避免出现空穴,防止晶格失配对于计算结果的影响,两侧选用6×6×10个氮化镓晶体组成基体,截面积为38.27 Å×38.27 Å,共计14 000个原子;中间是约38.34 Å×38.34 Å的石墨烯片,共574个碳原子。

3.2 模拟过程

在模拟过程中Ga、N、C原子之间的相互作用选用Tersoff势能[12],x和y方向采用周期性边界条件,时间步长取0.25 fs[13]。首先在NVT系综下运行0.25 ns,使系统达到设定温度,然后在NVE系综下运行;平衡后,同样为了防止能量的漂移,仍然采用改进的非对称热交换算法,设定的热流为2.0 eV/ps,得到所需要的温度梯度。

3.3 模拟结果

系统的温度分布如图7所示。

图7 系统温度分布Fig.7 Temperature profile of system

氮化镓与石墨烯之间的界面热导随温度的变化关系如图8所示。

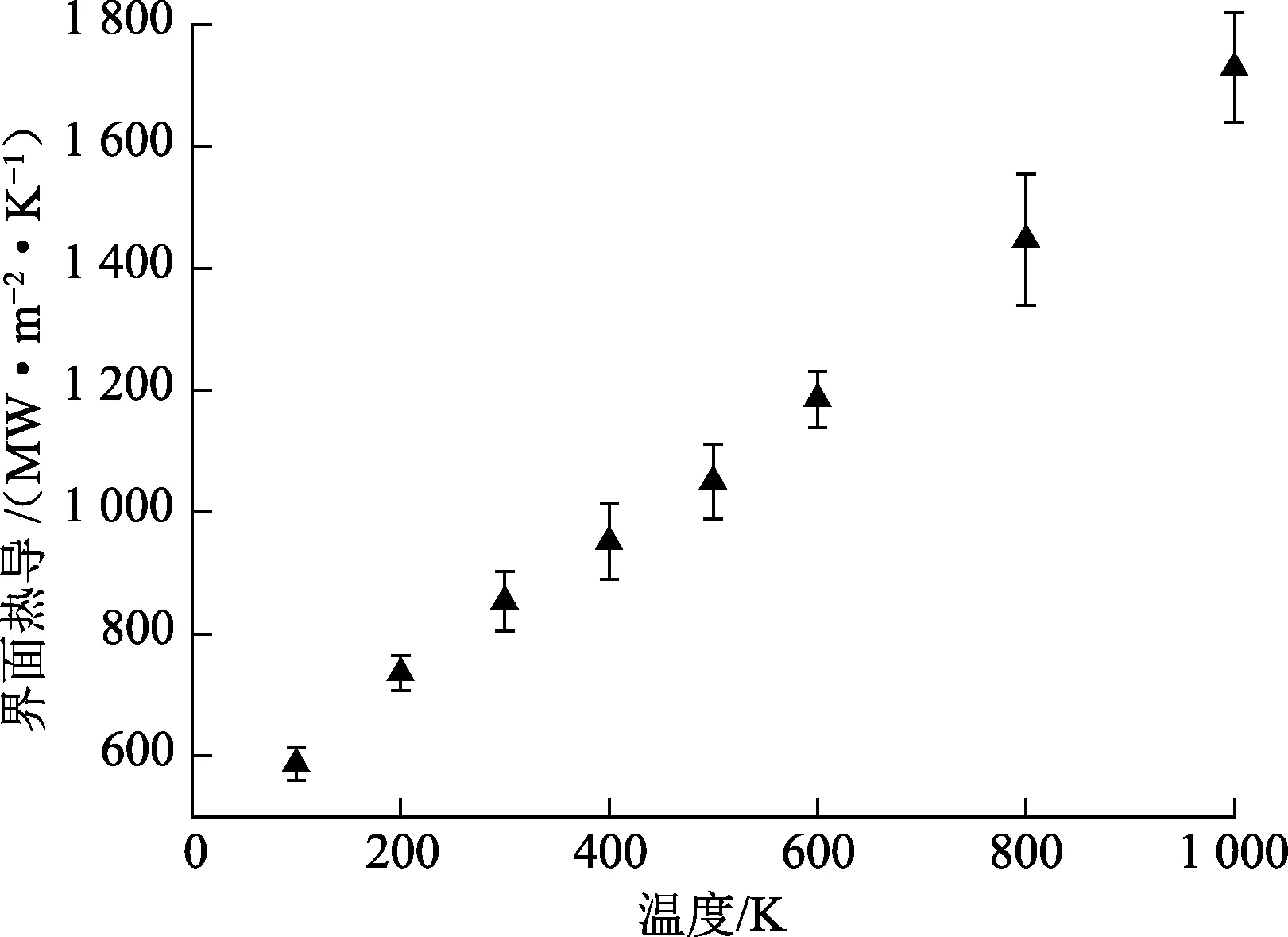
图8 氮化镓和石墨烯的界面热导随温度变化Fig.8 Changes of interfacial thermal conductivity of gallium nitride and graphene with temperature

由图8可以看出,随着温度升高,氮化镓和石墨烯之间的界面热导增大。图9为界面处的N、Ga、C原子的声子态密度曲线。由图9可以看出,频率在0～10 THz时,随温度升高,Ga的声子态密度降低,增大了其与碳原子的耦合程度,从而增大了界面热导。

图9 不同温度时界面处的Ga、N、C原子的声子态密度Fig.9 Vibration density of states of Ga, N, C at interface under different temperatures

4 石墨烯界面热输运对比

图10为氮化镓和硅基体与石墨烯界面热导的温度效应。从图10可以看出,硅与石墨烯之间的界面热导小于氮化镓和石墨烯之间的界面热导;且随着温度升高,氮化镓基体与石墨烯之间界面热导增大的趋势比硅基体要大;这是由于在高温下氮化镓的能量载流子主要是光学声子,且氮化镓中光学声子所占的比例很高,因此高温下的氮化镓热导率很高,这种情况下,意味着声子的散射率很低,在氮化镓中的输运效率很高。这样,作为能量载流子的声子更加容易通过界面;同时高的热导率意味着在同样的热流下具有更小的温度梯度,在界面处将有更小的温差,所以界面处会拥有更大的界面热导。

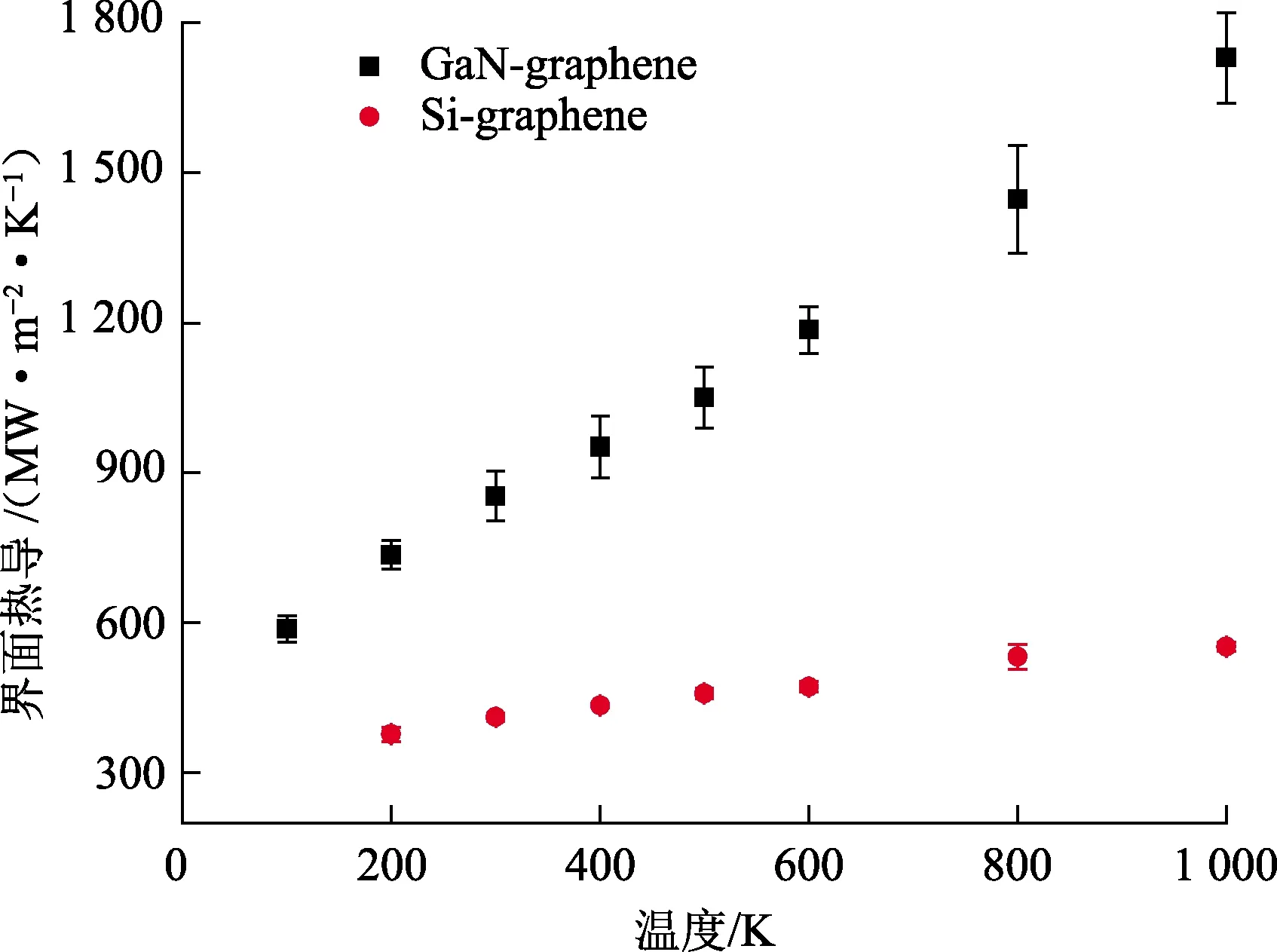
图10 氮化镓和硅基体与石墨烯的界面热导的温度效应Fig.10 Temperature effect of interfacial thermal conductivity of gallium nitride and silicon matrix and graphene

从图3中可以看出,硅原子的截止频率仅为20 THz,因此只在0～20 THz处两种原子发生耦合。而从图9中可以看出,镓原子的截止频率为40 THz,氮原子的截止频率更是达到60 THz,这大大增加了其与碳原子的VDOS重叠区域的耦合程度,提高了声子谱的匹配程度,从而利于界面热传递,即氮化镓基体与石墨烯之间的界面热导要大于硅基体与石墨烯之间的界面热导。