接触式机械密封端面的分形磨损模型*
2020-12-08李小彭杨泽敏潘五九王琳琳徐金池闻邦椿
李小彭, 杨泽敏, 潘五九, 王琳琳, 徐金池, 闻邦椿
(东北大学机械工程与自动化学院 沈阳,110819)
引 言
机械密封最主要的性能就是其密封性能,而引起接触式机械密封失效的最直接原因就是磨损,磨损速率在很大程度上影响着接触式机械密封的使用寿命和运转精度[1-2]。机械密封广泛应用于军工、航天以及化工领域的轴端密封中,因此,为了防止接触式机械密封磨损造成密封失效而引起巨大损失,从理论上揭示影响接触式机械密封磨损的因素,以此来指导生产中对磨损率的控制是十分必要的。
1961年,Mayer[3]利用圆环理论对密封端面的变形及摩擦磨损进行了研究,且Mayer的圆环理论对机械密封端面的研究奠定了基础。后来,Summers-Simith[4]研究了机械密封的磨损类型和影响磨损的因素等。王汝美[5]通过实验研究了各因素对机械密封磨损的影响。文献[6-7]介绍了如何利用实验统计数据来计算接触式机械密封磨损率,并给出了一种计算接触式机械密封磨损率的简易方法。房桂芳等[8]根据Archard磨损理论,建立了机械密封端面的分形黏着磨损模型。但运用的机械密封端面形貌是用余弦函数表示的,这与实际表面形貌还存在着一定误差。赵帅等[9]从材料角度研究了材料及表面织构对机械密封磨损的影响。文献[10]也从材料角度研究了丁腈橡胶材料的机械密封的微动磨损特性。
以上所有研究虽然都对机械密封的磨损进行了研究,但他们对机械密封端面的表面形貌的描述都存在一定的误差,因此最后得到的机械密封的磨损率也是有一定误差的。而分形理论的出现为准确描述机械密封的端面形貌提供了理论依据。因此笔者旨在基于分形理论对机械密封的磨损率进行计算,推导出计算模型,以期得到一个更准确的机械密封的磨损模型,并可以此来指导生产。
1 接触式机械密封端面分形磨损模型的建立
从微观角度来看,接触式机械密封的动静环接触端面是粗糙的,并且具有分形特性[11-12],可用W-M函数来描述接触式机械密封的端面形貌[13]。
1.1 接触式机械密封端面形貌的分形表征
根据修改后的M-B分形模型,可以把接触式机械密封的软质环与硬质环的接触简化为粗糙平面与理想刚性光滑平面的接触[14]。因此,接触式机械密封软质环端面轮廓曲线可用W-M函数来表示,即
(1)
其中:Z(x)为接触面轮廓随机高度;G为表面的特征长度尺度参数;D为接触粗糙表面的分形维数;γn为随机轮廓的空间频率;nl为轮廓结构的最低截止频率相对应的序数;γ为大于1的常数,对于服从正态分布的随机表面,通常取γ=1.5[15],且γnl=1/l;l为样本长度。
从微观角度看,接触式机械密封补偿环与非补偿环的接触实质上是接触式机械密封端面的微凸体的相互接触,如图1所示。接触式机械密封端面的接触部分承受轴向闭合力,且接触部分会产生磨损。
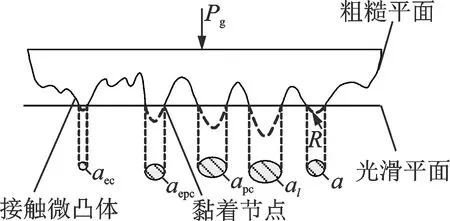
图1 接触式机械密封端面的分形表征Fig.1 Fractal characterization of mechanical seal face
图1中,pg为接触式机械密封的端面比载荷;aec为弹性变形转化为弹塑性变形的临界接触面积;aepc为第1弹塑性变形区与第2弹塑性变形区的临界接触面积;apc为第2弹塑性变形区与塑性变形区的临界接触面积;a为接触面微接触点的接触面积;al为接触面微接触点的最大接触面积;R为微凸体顶端曲率半径。
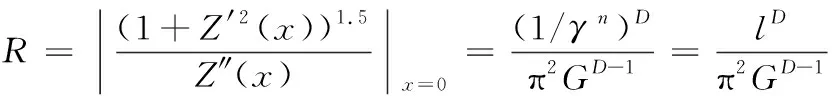
(2)
(3)
根据文献[16],可得到接触面微接触点的面积大小分布函数为
(4)
1.2 接触式机械密封的端面比载荷与实际接触面积
接触式机械密封端面的承载能力与其微接触点的变形承载能力有很大关系。研究表明[17],当对接触式机械密封施加轴向载荷时,软质环密封端面曲率半径较小的微凸体先发生弹性变形,然后随着载荷的增大,软质环的微凸体与硬质环的接触面积增大,并发生弹塑性变形,直至最后发生塑性变形。弹性变形转化为弹塑性变形的临界接触面积为
(5)
其中:K为较软材料的硬度系数,与材料的泊松比有关(K=0.454+0.410ν);H为较软材料的硬度;E为接触面综合弹性模量。
接触面的综合弹性模量可以表示为
(6)
其中:E1和E2分别为接触式机械密封硬质环和软质环的弹性模量;v1和v2分别为接触式机械密封硬质环和软质环的泊松比。
第1弹塑性变形区与第2弹塑性变形区的临界接触面积为
aepc=7.119 7aec
(7)
第2弹塑性变形区与塑性变形区的临界接触面积为
apc=205.382 7aec
(8)
根据文献[17],在各个变形区域,微凸体接触点负载与微凸体接触点接触面积之间的关系是不同的,具体如下
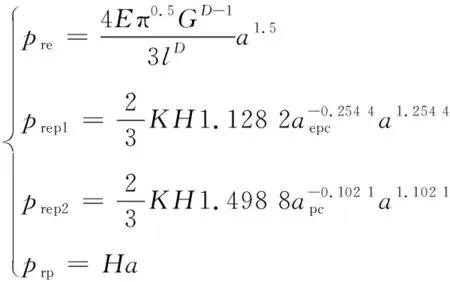
(9)
其中:pre为发生弹性变形的微接触点的承受载荷;prep1为在第1弹塑性变形区发生弹塑性变形的微接触点的承受载荷;prep2为在第2弹塑性变形区发生弹塑性变形的微接触点的承受载荷;prp为发生塑性变形的微接触点的承受载荷。
根据式(9)求出接触式机械密封端面总载荷与真实接触面积之间的关系为
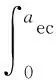
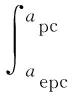
(10)
接触式机械密封的端面比载荷则为

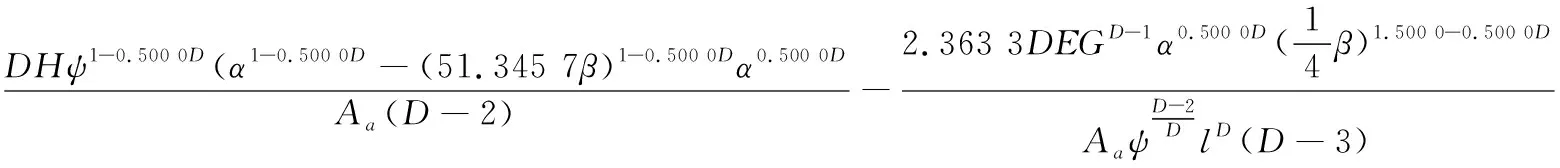
(11)
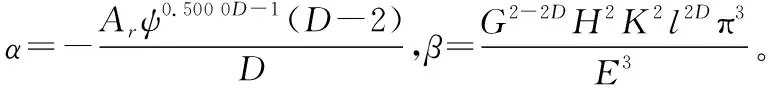
根据式(11)可以求出Ar,即
Ar=f(Aa,pg,H,K,E,l,D,G)
(12)
1.3 接触式机械密封的黏着磨损分形模型
根据经典黏着磨损理论[18],接触式机械密封的磨损主要体现以黏着磨损的形式。机械密封的软质环上的微凸体在外载荷作用下会黏结在硬质环表面上,当受到切向载荷作用时,相互作用微凸体中较弱的一方就会被剪断脱落,从而形成端面磨损。
接触式机械密封端面微凸体的形状一般近似为半球体,其底边圆直径为L,则单个微凸体的体积可以表示为
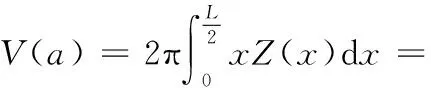
(13)
其中:L=a0.5[19]。
在接触式机械密封的两接触端面相对滑移L的距离时,黏着节点彻底切断,此时微凸体的黏着节点处就会形成一个磨屑,而这个磨屑的体积就近似这个微凸体的体积,即式(13)。那么,整个接触端面的磨屑体积可以表示为
(14)
整个接触端面产生ΔV体积的磨屑,所需接触式机械密封动静环的相对滑移时间t可表示为
(15)
其中:v为接触式机械密封接触端面的平均线速度,v=πrmn/30;n为接触式机械密封动环转速;rm为接触式机械密封接触端面的平均半径。
由文献[8]可知,实际上并不是所有黏着微凸体均会形成磨屑,固此处引入磨损系数KF(KF<1)来表示黏着微凸体形成磨屑的概率。因此根据Archard磨损理论,可得到接触式机械密封端面的磨损率为
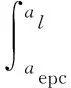
(16)
在计算式(13)时,因为W-M函数的核心是无数个余弦函数的叠加,因此为了方便计算,并表现出W-M函数的特征,取n从14叠加到15。
2 仿真分析
对式(16)所表示的接触式机械密封的磨损模型进行影响因素分析,分析分形参数、材料参数以及工作参数对接触式机械密封磨损的影响。在分析时,考虑接触式机械密封的常用材料以及加工方法,选用磨削加工的SiC-浸渍石墨组对的机械密封副进行研究[20],其材料参数与工况参数如表1所示。

表1 机械密封副材料参数与工况参数Tab.1 Material parameters and working condition parameters of mechanical seal
2.1 分形维数D对磨损率γ的影响
在研究分形维数D对接触式机械密封的磨损率的影响时,选取G=10-8m。
如图2所示,随着分形维数D的增大,接触式机械密封的磨损率γ先减小后增大,曲线形状呈浴盆曲线。即存在一个理论上的分形维数使得接触式机械密封的磨损率的最小,这个分形维数就是最优分形维数。这是因为分形维数D是反映表面具体细节、精细程度的参数,表面粗糙度随着分形维数的增大而减小。当D较小时,随着D的增大,表面粗糙度减小,接触区处于塑性接触的区域迅速减少,黏着磨损现象也大幅减少,因此磨损率减小;随着D的增大,该效果逐渐减弱,磨损率减小速度减缓;而当D增大到较大值时,表面精细程度太高,导致微接触面积大于临界变形面积aec的比例增大,从而使得黏着磨损现象增加,磨损率增大。
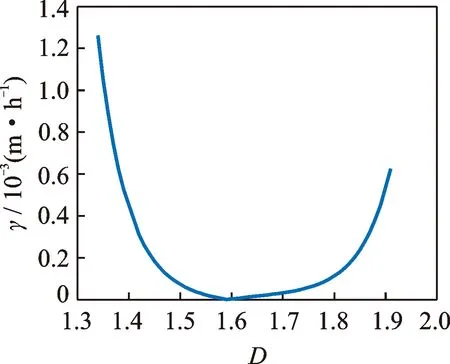
图2 分形维数D对磨损率γ的影响Fig.2 The influence of fractal dimension D on wear rate γ
2.2 特征长度尺度参数G对磨损率γ的影响
在研究特征长度尺度参数G对接触式机械密封的磨损率γ的影响时,取分形维数D=1.45。
如图3所示,随着特征长度尺度参数G的增大,接触式机械密封的磨损率γ也在增大,但是增大速率在逐渐减小。这是因为特征长度尺度参数G越大,表示端面就越粗糙,因此,初期随着特征长度尺度参数G的增大,接触式机械密封的磨损率γ会增大的比较多;而当G增大到一定值后,机械密封端面已经很粗糙了,再使其增加对磨损率γ的影响也就不那么明显了,增大速率也就会越来越小了。

图3 特征长度尺度参数G对磨损率γ的影响Fig.3 The lnfluence of characteristic length scale parameters G on wear rate γ
2.3 综合弹性模量E对磨损率γ的影响
在研究综合弹性模量E对接触式机械密封的磨损率γ的影响时,取分形维数D=1.45。
如图4所示,随着综合弹性模量E的减小,接触式机械密封的磨损率γ有所增加,尤其是在特征长度尺度参数G比较大时,即接触端面比较粗糙时。这是因为综合弹性模量E的减小,不是因为硬质环弹性模量E1的减小,就是软质环弹性模量E2的减小,而把硬质环假设为了刚体,因此只需考虑软质环弹性模量E2的减小。随着弹性模量的减小,材料会越来越容易发生塑性变形,这就使得黏着磨损现象增加,因此磨损率γ也就会增大。
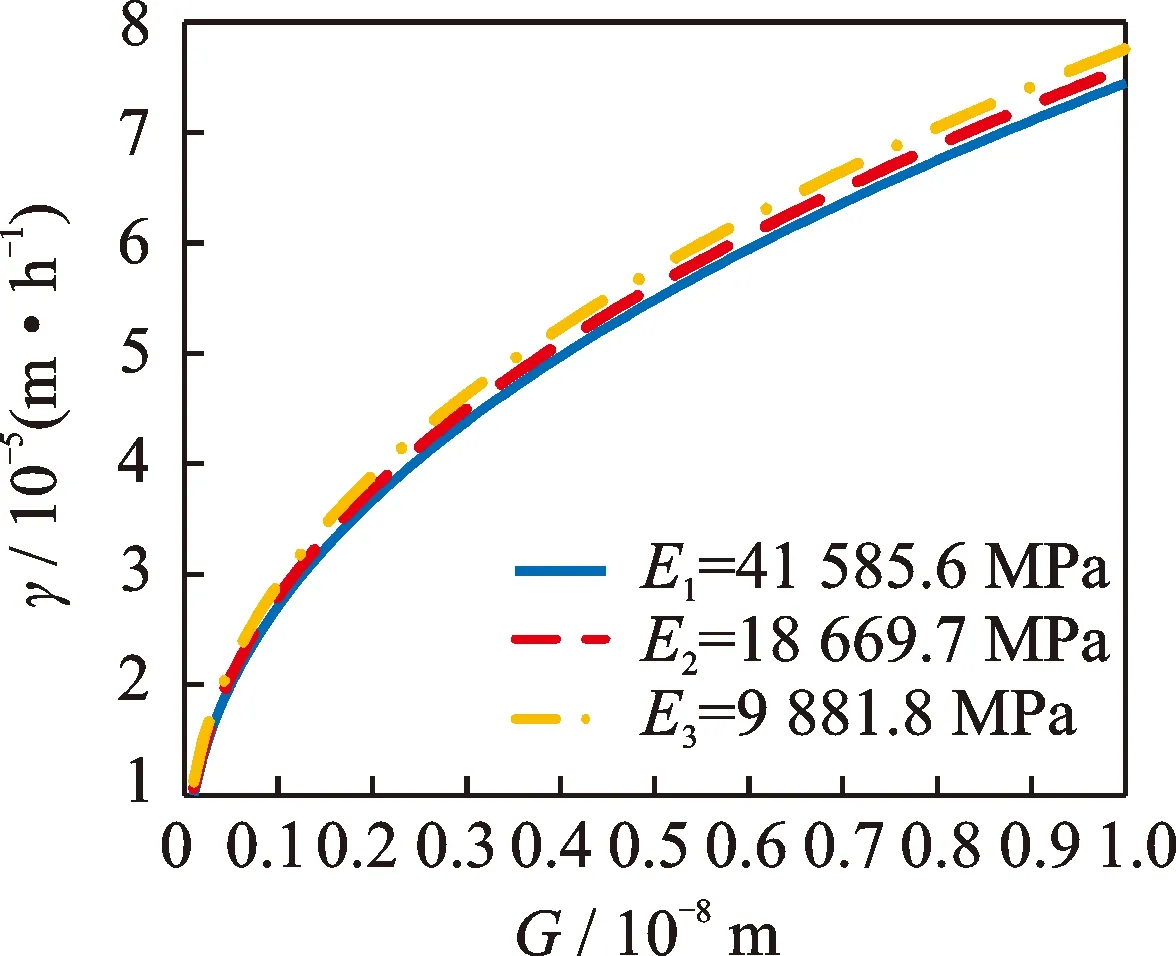
图4 综合弹性模量E对磨损率γ的影响Fig.4 The influence of integrated modulus E of elasticity on wear rate γ
2.4 端面比载荷pg对磨损率γ的影响
在研究端面比载荷pg对接触式机械密封的磨损率γ的影响时,取分形维数D=1.45。
如图5所示,在相同的特征长度尺度参数G下,随着端面比载荷pg的逐渐增大,接触式机械密封的磨损率γ也会逐渐增大。这是因为随着端面比载荷pg的逐渐增大,接触式机械密封微凸体的塑性变形会逐渐增多,从而使得黏着磨损现象增多,它的磨损率也就随之增大。
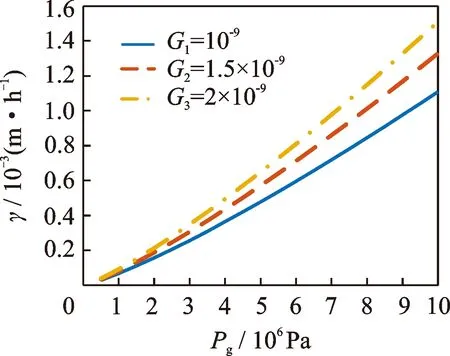
图5 端面比载荷pg对磨损率γ的影响Fig.5 The influence of the end surface specific load pg on wear rate γ
2.5 转速n对磨损率γ的影响
在研究接触式机械密封的转速n对磨损率γ的影响时,取分形维数D=1.45。
如图6所示,在相同的特征长度尺度参数G下,随着转速n的增大,接触式机械密封的磨损率γ也在增大,而且是近似于线性的增大。这是因为随着转速n的增大,相同时间内,接触式机械密封的软质环与硬质环的相对滑移距离增大,微凸体的摩擦次数增多,磨损率γ也就随之增大。
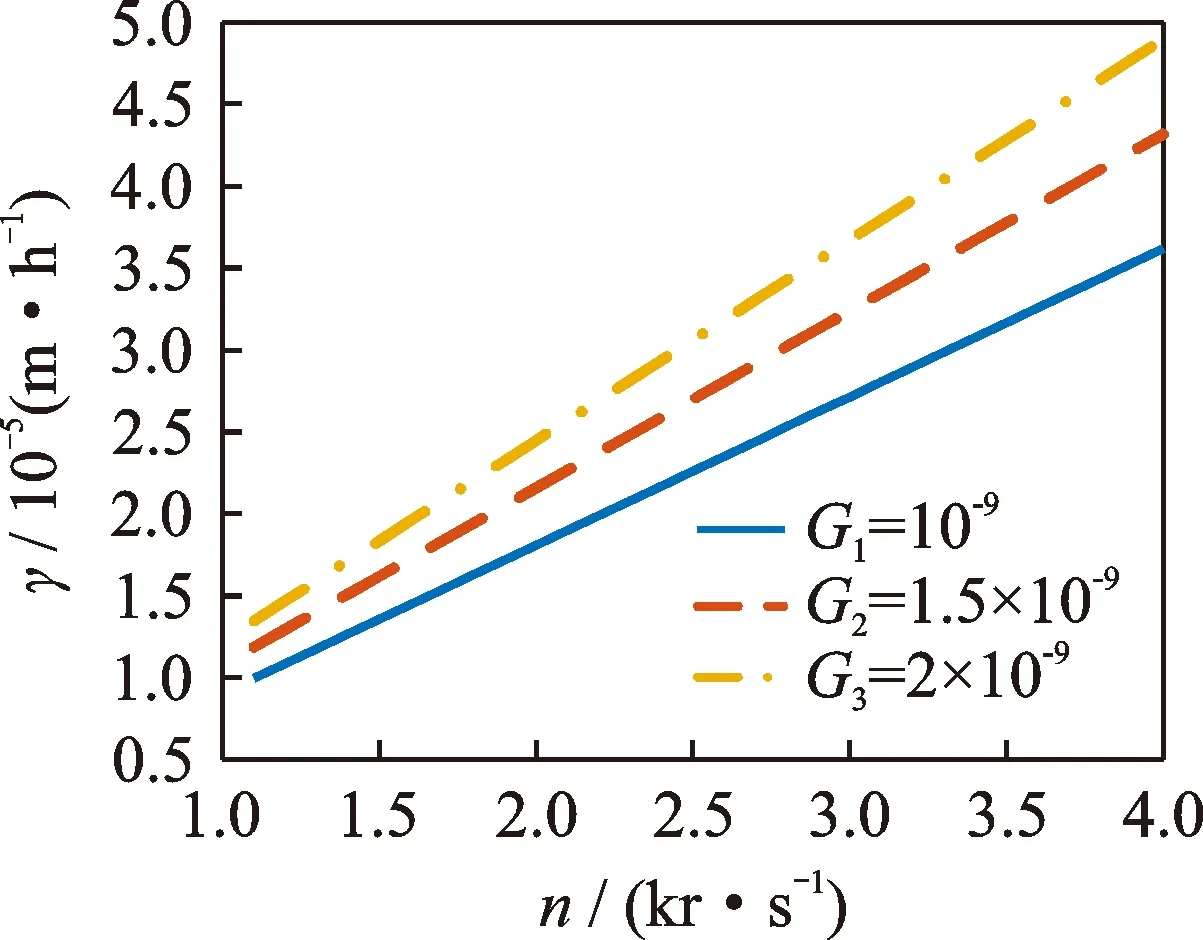
图6 转速n对磨损率γ的影响Fig.6 The influence of rotational speed n on wear rate γ
3 实验对比
笔者引用文献[20]实验中对磨损量的测量与文中所建模型进行对比,结果如图7所示。从图7中可知,本模型较好地模拟了接触式机械密封端面的磨损率,与实验数据的误差相对较小。模型计算值与实验测量值存在误差的主要原因有:忽略了机械密封端面各微凸体变形时它们之间的相互影响;由于所建模型的W-M函数为了方便计算,只用了两项余弦函数相叠加;分形磨损系数KF应该是随着时间变化的,而文中选择的是一个定值。
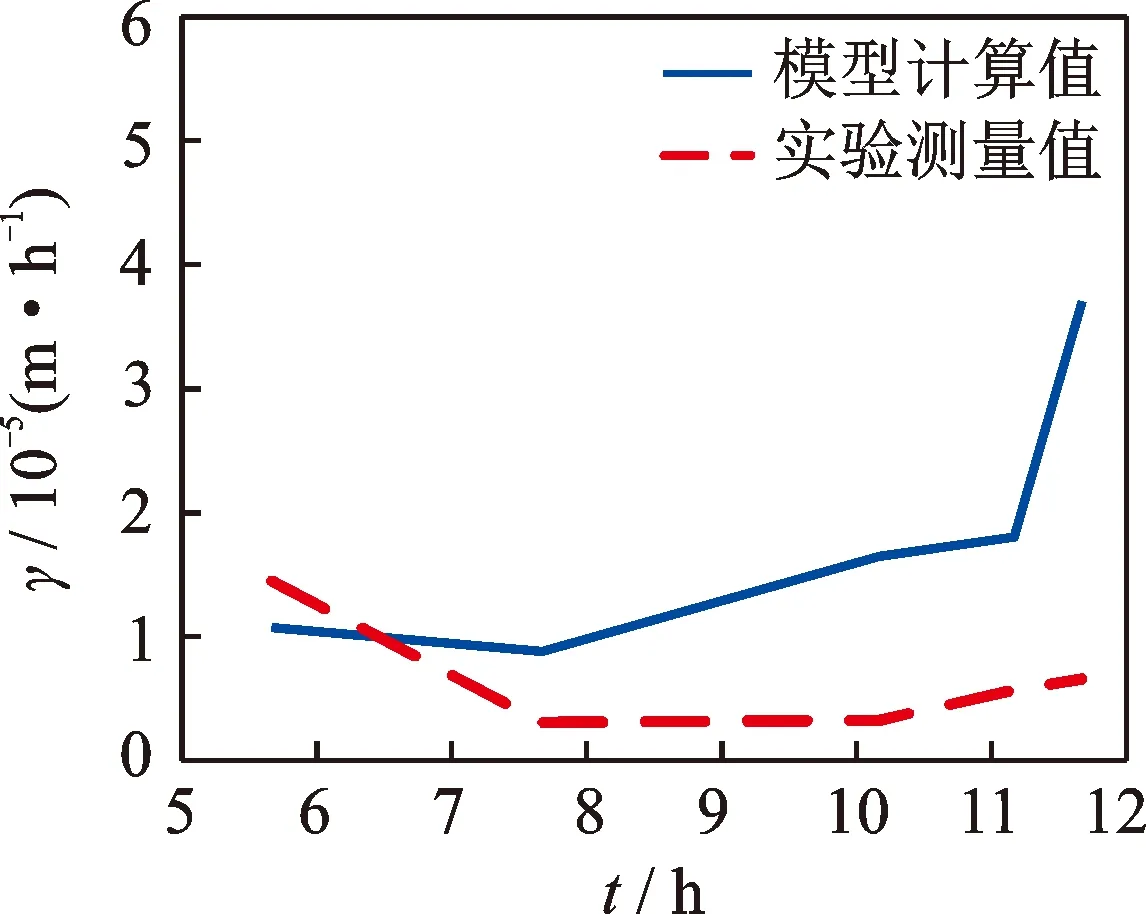
图7 实验对比Fig.7 Experimental comparison
4 结 论
1) 本研究基于分形理论建立了接触式机械密封端面磨损模型,研究了机械密封端面微观形貌、工作参数及材料性能与磨损的关系,为磨损预测提供了理论指导。
2) 接触式机械密封分形维数D与其磨损率γ的关系呈浴盆曲线,即存在最优分形维数使得磨损率最小(D=1.55附近);而特征长度尺度参数G与其磨损率γ成正比。因此在制造过程当中,应尽量使接触式机械密封的分形维数D靠近最优分形维数,并减小特征长度尺度参数G。
3) 通过数值分析,接触式机械密封的端面比载荷pg、转速n均与其磨损率γ成正比,而综合弹性模量E与磨损率成反比,这可验证接触式机械密封端面的分形磨损模型的正确性。
