离心泵负载下的电机定子电流特性研究*
2020-12-08袁寿其韩岳江
龚 波, 袁寿其, 骆 寅, 韩岳江, 董 健
(江苏大学国家水泵及系统工程技术研究中心 镇江,212013)
引 言
离心泵被广泛应用于生产和生活中,监测离心泵运行状态,保证离心泵的安全可靠运行一直是众多学者研究的焦点。陈长盛等[1]研究了利用了振动信号来监测离心泵运行状态。Pavesi等[2]利用压力脉动信号来监测离心泵内部不稳定流动。这些方法使用的传感器普遍成本高、安装难度大;使用的数据采集、传输、分析系统一般较复杂,信号采集容易受到干扰,结构可靠性较低[3]。
基于电机定子电流的监测技术兴起于20世纪70年代,其原理是将感应电动机作为转矩传感器,通过监测电机定子电流信号来监测电机负载的运行状态。国内多用此技术来诊断电机本体的机械部件的故障,而鲜有将其运用于离心泵状态监测上。
由电机驱动的离心泵在运行过程中,叶轮叶片会受到输送介质的反作用力[4],形成水力负载转矩。水力负载转矩在轴上传递,最终传递到电机转子轴端,并在电机的定子电流上形成响应,因此监测和分析电机定子电流即可实现离心泵的状态监测。Siegler等[5]就将这种监测方法应用于海水淡化泵叶轮腐蚀程度的监测上,其准确率高达90%。此后,美国橡树岭国家实验室(oak ridge national laboratory,简称ORNL)对此方法进行了深入研究,ORNL主要是利用电机定子电流监测法诊断泵部件的结构故障。Casada[6]研究了离心泵各工况下转子不对中时的定子电流和瞬时功率的时频特征。Ahonen等[7-8]建立了一种通过变频器来实现离心泵运行工况监测的方法,通过从变频器中读出当前电流值和电机的转速,根据已知的泵特性,计算出当前泵的运行工况。
相比于振动信号监测法[9]和压力脉动监测法等,利用电机定子电流信号分析(motor current signature analysis,简称MCSA)方法监测离心泵运行状态具有以下优点:①非接触式测量,无需直接在监测设备上安装传感器;②采集的信息集成度高,电机及其负载的几乎全部信息都通过电机定、转子绕组间的气隙磁场变化反映在定子电流中;③能用于振动噪声分析法等不能应用的场合,如潜水泵等[10]。
在离心泵与电机组成的系统中,当前关于定子电流的研究工作集中于故障特征频率的提取和故障信号能量变化的计算[11],却很少有关于离心泵运行在多工况下电机定子电流信号特征的研究。文中以IS-65-50-160型单级单吸离心泵和Y160M-2 B3型电机组成的系统为对象,研究离心泵不同工况下的电机定子电流特性,从定子电流中提取与离心泵运行相关的信息,为实现用定子电流监测离心泵运行和分析离心泵内部流动状态提供参考。
1 数值模拟与理论分析
在水泵中,转子轴系上的叶轮叶片会受到输送流体介质的反作用力,产生反向扭转力矩。泵在不同工况、流态下运行会产生不同的扭转力矩[12-14]。扭转力矩经过转子轴系传递后会在电机转子上产生扭转响应,电机的转子与定子之间存在磁耦合现象,可以通过提取、分析电机定子电流来分析离心泵运行工况。如图1所示,若能获得不同流态下水力负载转矩特征及其经过泵转子轴系传递后的在电机定子电流中响应特性,就可依据电机输出信号实现流态诊断。因此基于计算流体动力学(computational fluid dynamics,简称CFD)技术模拟了不同工况下的离心泵水力负载转矩特征,通过理论分析电机定子电流与离心泵负载转矩的关系,并用试验提取了离心泵不同运行状态下电机定子电流的特征。

图1 基于电机电流信号监测泵状态原理Fig.1 Condition monitoring principle of pump based on MCSA
1.1 离心泵非定常水力负载矩分析
文中选用IS-65-50-160型单级单吸离心泵的设计参数为:设计流量Qd为50 m3/h,扬程为37 m,转速为2 900 r/min,比转速为81.5,叶片数为6。对离心泵进行3维建模,对过流部件进行网格划分,所有网格均为6面体网格,网格质量均满足非定常计算要求,并对网格无关性进行了验证,最终确定全流场网格总数为2 926 876。图2为离心泵流道网格划分图。对全流场进行模拟计算,可获得离心泵在各个工况点下的水力矩特征。图3为不同工况下的水力矩时域图。可见,在不同工况下水力矩均成周期性变化,且水力矩整体值随流量Q增大而增大。水力矩的脉动分量强度随运行工况点偏离设计点的距离增大而增大,水力矩脉动分量强度的RMS值如图4所示。

图2 离心泵流道网格划分图Fig.2 Mesh of model pump flow field
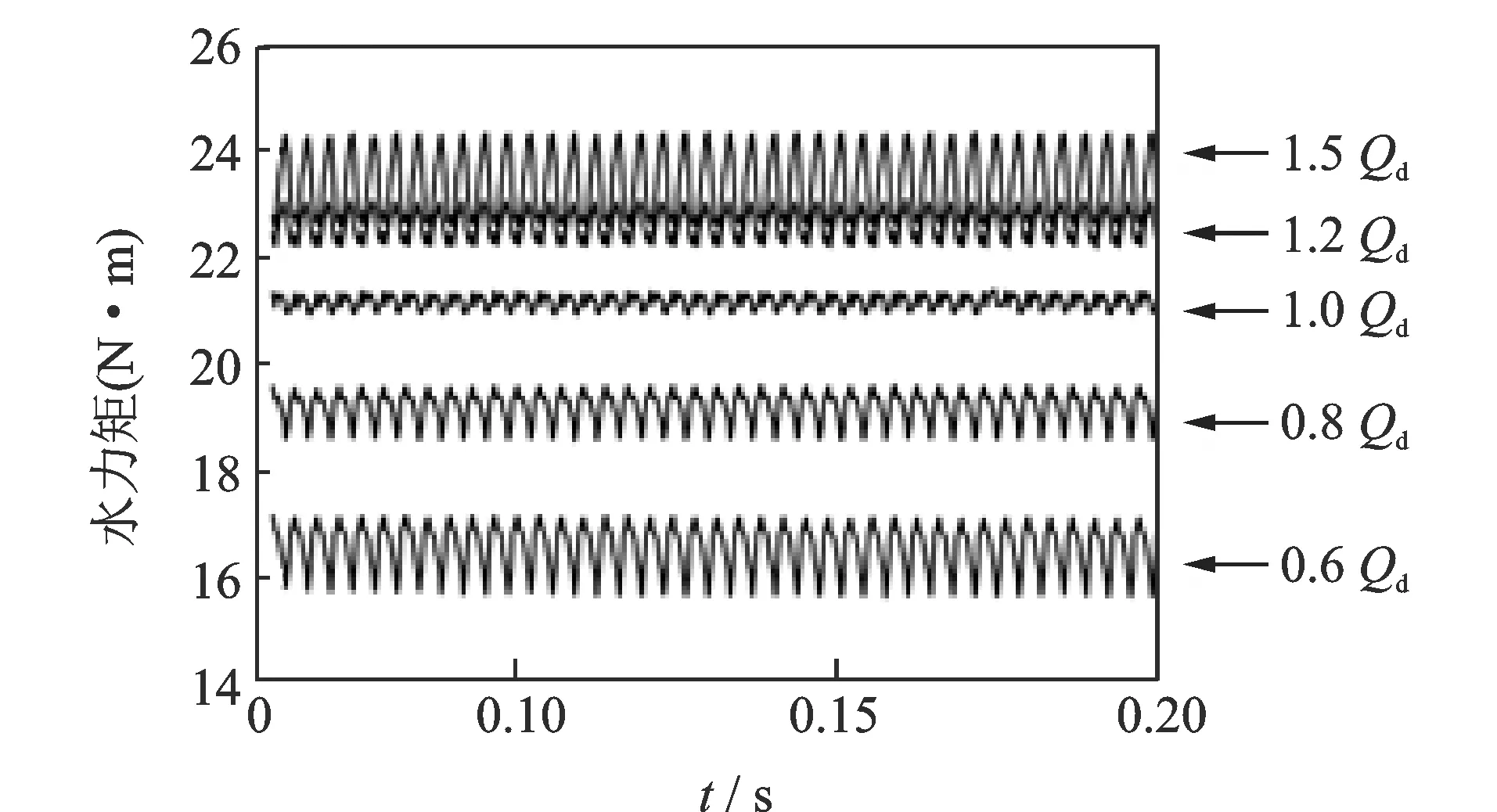
图3 不同工况下的水力矩时域图Fig.3 Time domain of hydraulic moment fluctuation under different operating conditions
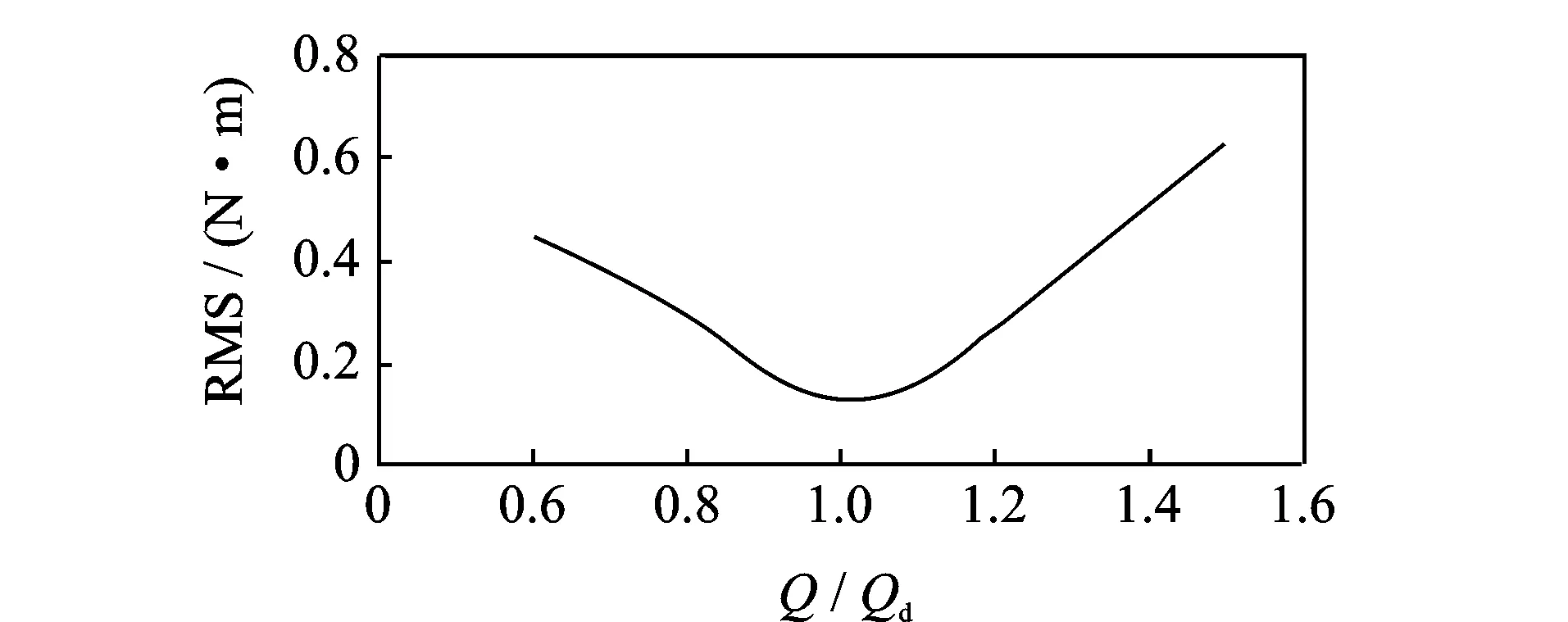
图4 不同工况下的离心泵水力矩脉动的RMS值Fig.4 RMS of hydraulic moment under different operating conditions
对水力矩时域信号进行快速傅里叶变换(fast Fourier transform,简称FFT)得到水力矩脉动分量的频谱图。在水力矩频谱图中,叶频分量f2在水力矩脉动强度变化中居于主导地位,如图5所示,其中:f2为叶频;f为频率变量。
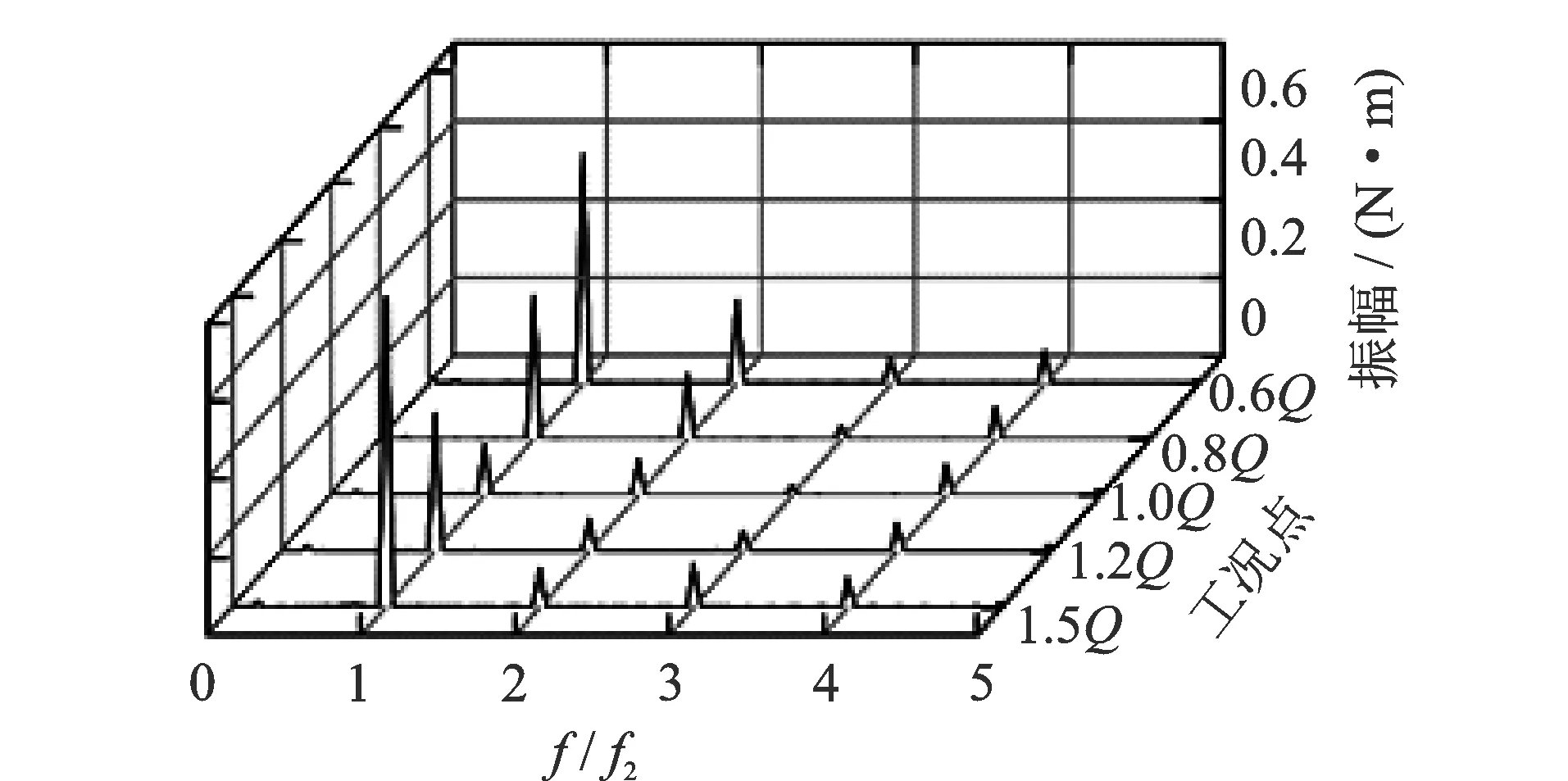
图5 不同工况下离心泵水力矩脉动分量频谱图Fig.5 Frequency domain of hydraulic moment fluctuation under different operating conditions
水力矩经过转子轴系传递后会在离心泵轴端产生对应的扭矩响应,并最终作为负载施加到电机上。通过水-机-电的联合仿真,即通过Fluent进行水力矩非定常计算,通过Workbench进行轴系扭矩的提取,运用神经网络进行水力矩到电机负载转矩的辨识,通过Simulink进行电机建模,并用Fluent中的自定义函数功能(user defined function,简称UDF)与Matlab脚本文件的编写实现Fluent与Simulink的数据传递,水力矩与轴端矩在稳态时相等,在瞬态时相关性也极高,总体上可视为相等[15]。湍流、边界层旋涡脱落等不稳定流动现象及不平衡的旋转质量等机械因素也会一定程度上造成轴端扭矩的波动,但这些比水力矩脉动作用要小很多。
1.2 交流感应电动机数学模型
交流感应电动机系统数学模型[16]可以表示为

(1)
其中:第1个式子是传动系统的转矩平衡方程式,Te,TL,J,pn,ω分别为电磁转矩、离心泵负载引起的轴端扭矩、机组的转动惯量、电机极对数及旋转角速度。
由第1个式子可见,TL存在扰动时会引起ω发生变化。第2个式子为电机电压平衡方程。式中u,R,i,L分别为电机定子电压、电阻、电流和电感参数,θ为机械扭转角。式中的第2项和第3项为电磁感应电动势,Ldi/dt是由于电流变化引起的感应电动势,ωidL/dθ为转子和定子之间的相对位置变化引起的感应电动势。
由于电网容量较大,u可视为不随负荷变化。结合转矩平衡方程可知,当轴端扭矩TL存在扰动时会导致ω变化,会导致i发生变化,i的改变最终会改变Te,从而形成新的转矩平衡。
可以看出,电流、磁通、扭矩之间的关系较复杂,不能直接由电流的变化情况反映扭矩波动情况。在此采用M-T坐标变换[17]法将问题简化得到各向电流与产生Te的电流分量isT和产生恒定的有效磁通的励磁电流分量isM的关系。
(2)
简化后的电磁扭矩、磁场、电流的关系可用下式表示
(3)
其中:P为电机的结构常数;λs为定子磁通,与电机输入电压、电机结构和负载相关,在泵与电机组成的系统中离心泵可视为稳定负载,扰动转矩对电流的影响很小,所以λs可视为常数。
因此,可认为Te与其电流分量isT线性相关。由此可见,虽然isT不能直接测量,但通过坐标变换,isM,isT与相电流之间有着定量关系,因此电磁转矩可以间接反映在定子电流中。
假设转轴扭矩的扰动频率是f0,则感应电动机的气隙扭矩T包括平均转矩T0和轴转矩波动T1之和
T=T0+T1cos(2πf0t+φ)
(4)
其中:φ为电机转轴可能产生的扭振相位。
定子电流由isM和isT组成。isM和isT可分解为平均部分和波动部分
Is M=Is M0+As Msin(2πf0t+φM)
(5)
IsT=IsT0+AsTsin(2πf0t+φT)
(6)
因此,各相电流可分解成isM和isT的组成形式,如A相
Is a=Is Msin(2πfet)+IsTcos(2πfet)
(7)
化简可得
(8)
其中:IsM0=I0cosφ0;IsT0=I0sinφ0;φ0=tan-1(IsT0/IsM0)
由式(8)可看出,扭矩的波动频率f0会对电网工频形成调制;定子电流主要由平均电流分量和波动电流分量组成,平均电流对应的频率为fe,波动电流在f0-fe和f0+fe处会有对应的分量,且f0-fe处的幅值要大于f0+fe处。由前面分析知水力矩与轴端扭矩可认为近似相等,水力矩脉动是造成轴端扭矩波动的最主要原因,因此水力矩脉动的频率对应的为轴端扭矩的波动频率f0,以调制的方式反应在定子电流信号中。
其他因素,如湍流、边界层旋涡脱落等不稳定流动现象以及不平衡的旋转质量等机械因素,也会一定程度上导致扭矩的波动,但是其影响会远远小于水力矩的影响,并最终也反映在定子电流谐波中。
仔虾期饵料投喂用配合饲料(虾片)与大卤虫轮投,每2~3h一次,并随时观察仔虾胃肠饱满情况适时加以调整,以满足仔虾摄食量的要求。此阶段水温控制在25~26℃,出池前5d逐渐将水温降至自然温。日换水量为1/2左右,换水网箱网目为40目。充气量呈翻腾状,以防止饵料沉积,败坏水质。适度保持水中大卤虫数量(每升水1~2个),避免仔虾期出现残食现象。
2 试验与数据采集
在江苏大学国家水泵及系统工程技术研究中心实验室的闭式试验台上对离心泵进行测试。试验装置由储水罐、真空泵、进出水管阀、电机、测试泵、涡轮流量计、压力传感器、扭矩仪、轴编码器、直流稳压电源等组成。试验装置示意图如图6所示,装置现场布置图如图7所示。试验采集的数据有流量、进、出口压力等,采集频率为10 kHz。其中涡轮流量计安装在排出管路上,基本误差限为;进口阀门为手动式蝶阀,出口阀门为电动阀门,阀门控制器的精度可达0.1%;进出口压力传感器均为WIKA S-10型,精度为0.25%,安装在进口法兰上游和出口法兰下游2倍的管径处;采集的数据通过采集板卡NI-USB6343传输到计算机,由计算机完成数据的处理和运行的控制;通过霍尔传感器测得电机定子电流。
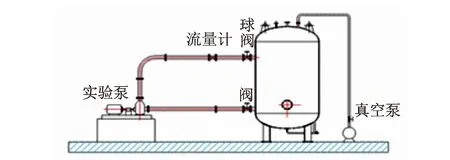
图6 试验装置示意图Fig.6 Schematic of experimental rig

图7 试验台Fig.7 The test platform
整个测试系统是基于NI公司的虚拟仪器技术,结合了PXI系统和多功能动态数据采集卡组成的硬件测试系统与由LabVIEW开发的软件系统,最终形成的一套自动采集数据的系统。其测试原理如图8所示。
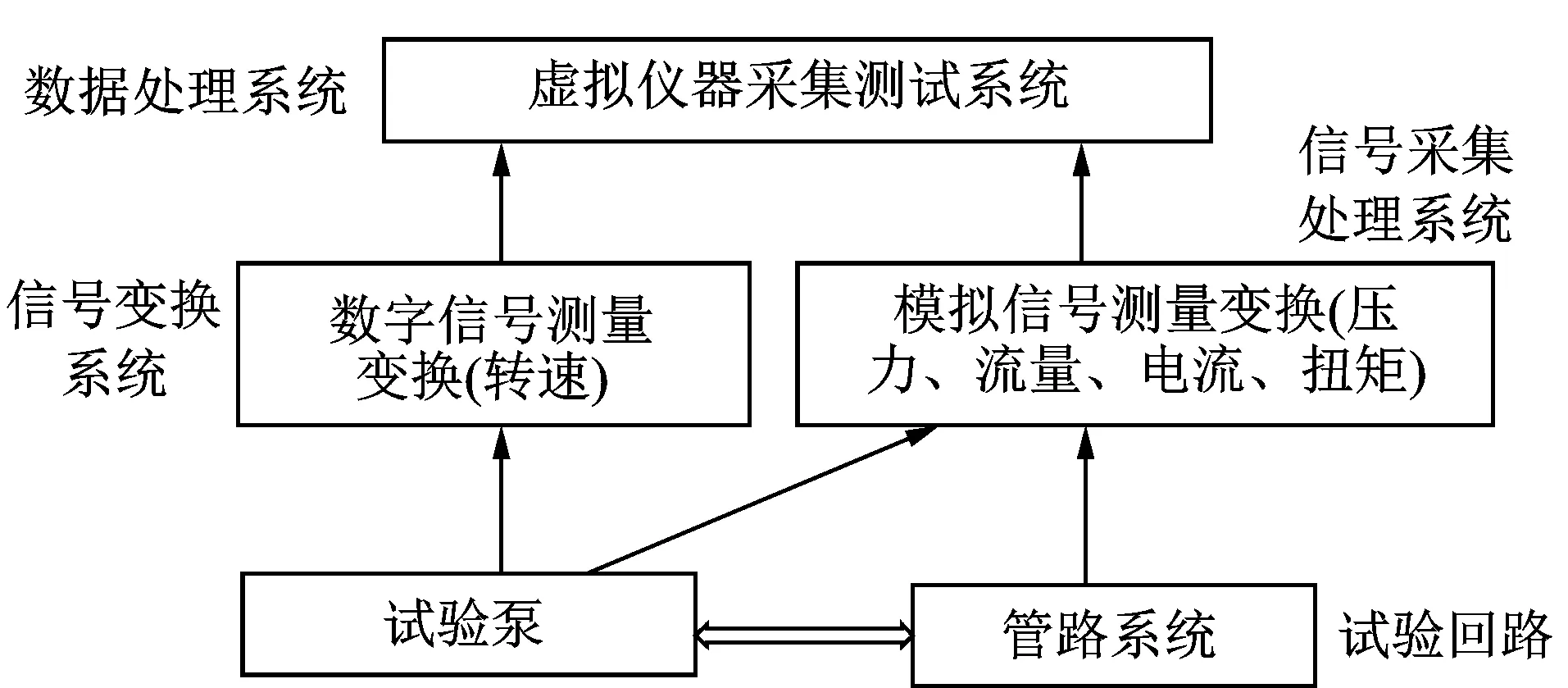
图8 测试原理Fig.8 The principle of test system
通过调节出口电动阀门来改变离心泵运行工况,调节阀门后静待2 min至工况稳定,开始记录采集到的数据,采样频率为10 kHz,连续采集10 s并保存。再次调节阀门,重复上述操作。直至采集到0.1Qd, 0.2Qd,0.3Qd, 0.4Qd, 0.5Qd, 0.6Qd, 0.7Qd, 0.8Qd, 0.9Qd, 1.0Qd, 1.1Qd, 1.2Qd和1.3Qd工况下的试验数据,结束试验。
3 试验结果与信号预处理
为了使得试验数据更加可靠,对每个工况点的试验数据持续采集10 s,取10 s内的平均值,计算得到相关的扬程功率等。根据3次外特性试验中采集到的数据绘制该泵的外特性曲线,如图9所示。
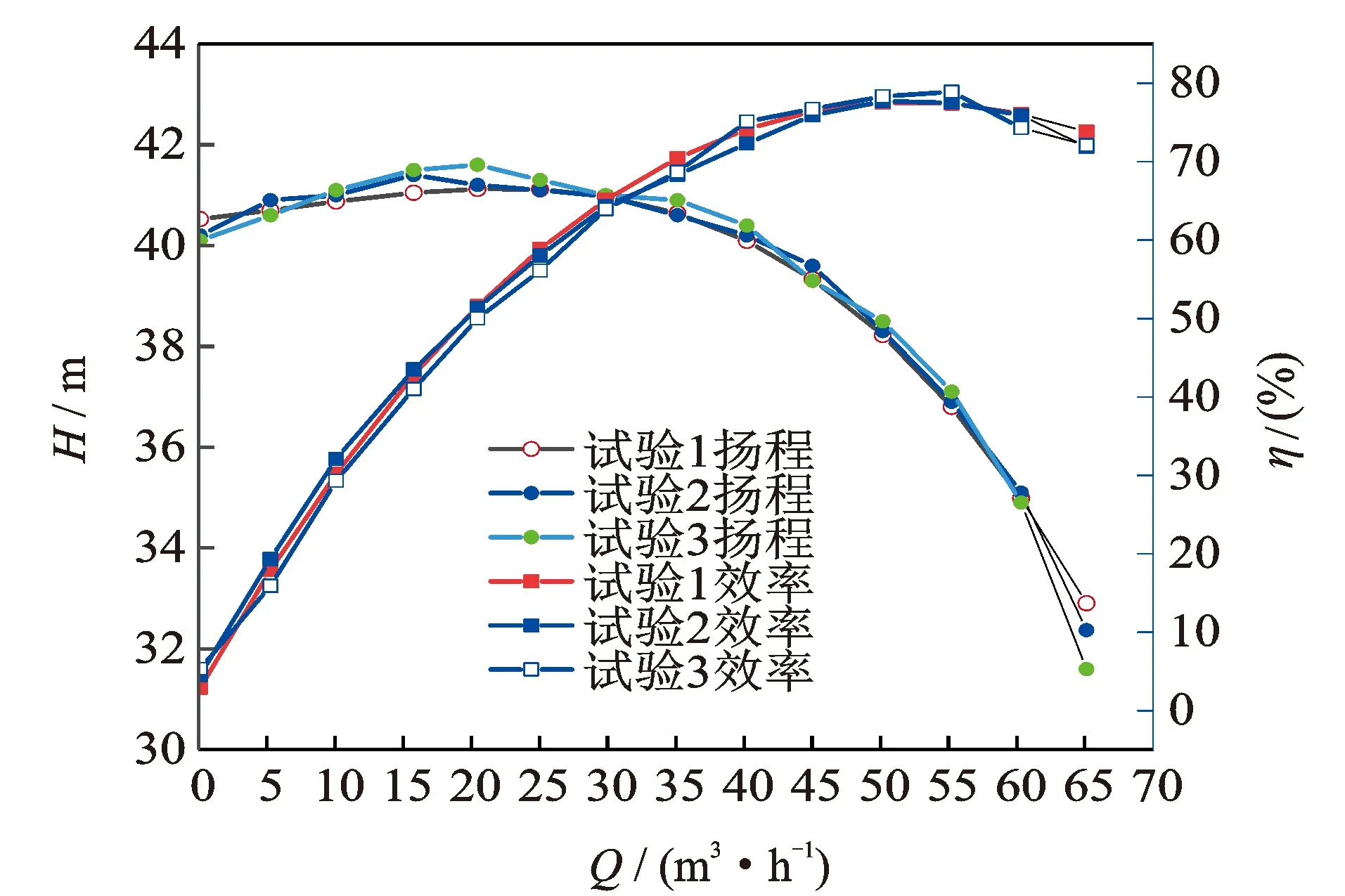
图9 测试泵外特性曲线Fig.9 Performance characteristics of the test pump
从图9中可以看出,3次试验曲线基本一致,可见试验数据可靠性较高。由扬程特性曲线看出,该泵的扬程性能曲线存在着驼峰现象,当流量在0~20 m3/h时,扬程随流量的增加呈小幅增加趋势,当流量大于20 m3/h时扬程随流量增加呈下降趋势。小流量(0~20 m3/h)下离心泵内部流动不稳定,流动损失较大,此时离心泵内部流体的流动不稳定可能会使得泵产生较大振动,也会造成泵轴上扭矩的波动,产生更多的谐波。由效率曲线可以看出,当离心泵运行在设计工况附近时效率较高,因为当离心泵运行在设计工况附近时流动更稳定,水力损失较小;当离心泵运行偏离设计工况时,因为离心泵偏离设计工况运行时水力损失较大,导致效率降低。
3.1 定子电流信号时域分析
定子电流的时域图如图10所示。由图10可知,定子电流总体上符合正弦交流信号特征,频率为与电网工频相同的50 Hz,可见电网工频信号在定子电流中占据着主导地位,而离心泵负载转矩波动导致的定子电流波动则较弱。对比标准工况下的电机定子电流信号与电源电流发现,其与电源电流正弦交流信号波形有些许偏差,这种偏差可能与离心泵负载有关。定子电流信号的平均大小随着离心泵运行工况而改变,可采用RMS来衡量定子电流的平均大小。定子电流的均方根随流量的变化趋势如图11所示。
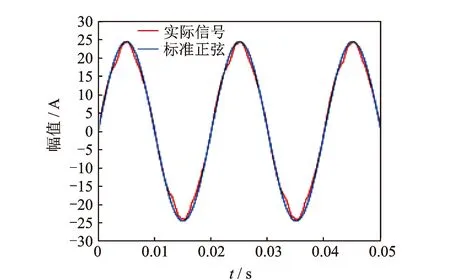
图10 设计工况下的定子电流时域信号Fig.10 Stator current time domain signal at the design point
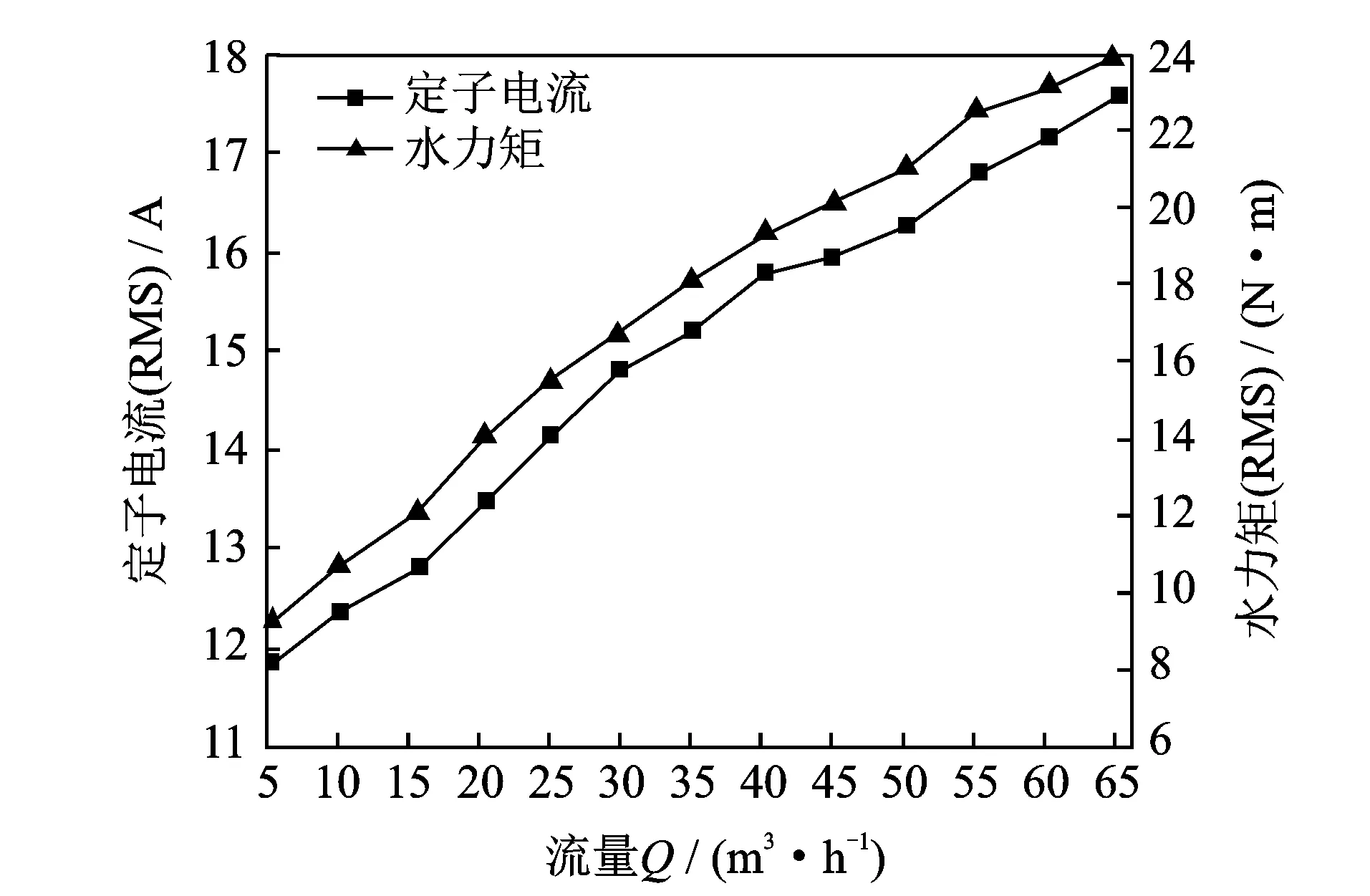
图11 定子电流和水力矩随流量变化图Fig.11 Stator current value and hydraulic torque versus operation point
从图11中可见,定子电流与离心泵水力矩随运行工况变化的规律相似,这主要是因为流量的增大流体对叶片的反作用增大导致水力矩增大,水力矩增大使得轴端扭矩增大,电机的输出功率增大,反应在定子电流中为定子电流的增大。因此,定子电流在一定程度上可作为运行工况监测的参考指标。
3.2 定子电流信号的频域分析
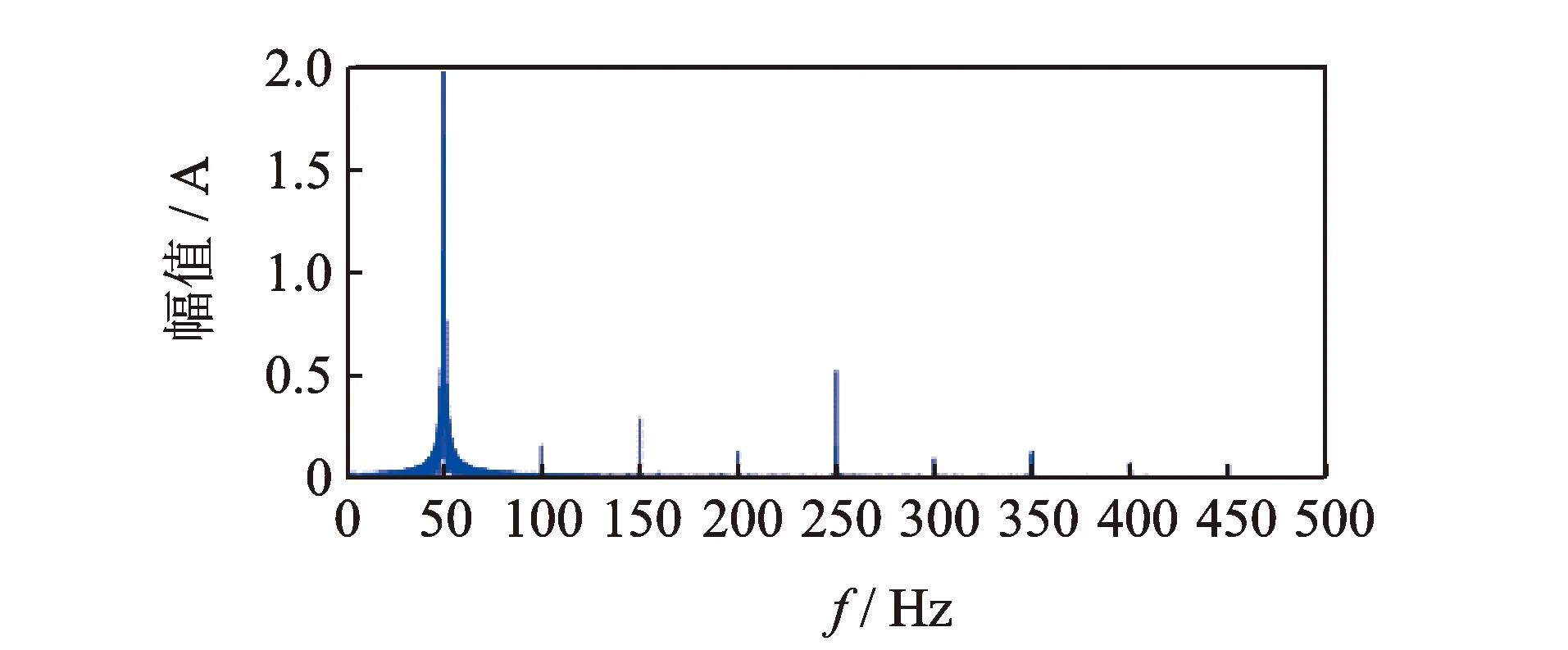
图12 设计工况下定子电流频谱图Fig.12 Frequency characteristic component of the stator current at the design point
3.2.1 定子电流信号的预处理
为了更好地比较不同工况下的定子电流特征,将定子电流按照式(9)作归一化处理,以便在相同的幅值区间内比较不同工况下的定子电流特征。
I1=(I-Imin)/(Imax-Imin)
(9)
奇异值分解法(singular value decomposition,简称SVD)[18]是一种消除电网工频干扰获得弱信号的有效方法。SVD是一种起源于线性代数的矩阵分解法,其基本原理在于通过SVD处理后信号中的特征成分被分解到不同的正交子空间,在定子电流中,电网工频在定子电流信号中占据着主分量地位,因此电网工频会被分解到第1主分量对应的相空间中,这样就可以剔除电网工频对应的电流分量。
奇异值分解法首先需将一组离散的定子电流信号重构成一个N×M的矩阵A,其中M为一个周期的信号长度[19]。
(10)
然后,将矩阵A分解成U,Λ,V相乘的形式[10]
(11)
取U中第1列u1,Λ中第1个元素σ1,V的第1列v1转置相乘构成矩阵,即为基频对应的奇异矩阵
(12)
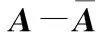
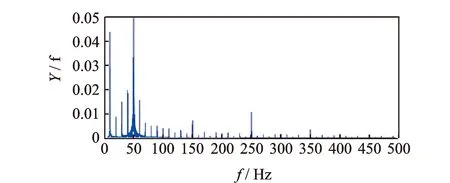
图13 消除电网工频后设计流量下定子电流频谱图Fig.13 Current spectrum after elimination of power frequency at the design point
对比图12,13可知,经过SVD处理后,50 Hz轴频是主要频率,之前被淹没在电网电流信息中的与离心泵运行状况相关的弱信号开始显现出来,信噪比得以提升。
3.2.2 谐波分析
轴端扭矩的波动会以谐波的形式反映在电机定子电流中[20]。总谐波失真(total harmonic distortion,简称THD)是指所有高次谐波幅值均方根与基频幅值之比。THD反映的是谐波成分的大小,高的谐波失真值意味着高次谐波成分越多,扭矩波动愈强烈,因此计算定子电流的总谐波失真值可用来判断扭矩波动情况,进而反映泵内的流动状态的稳定性。
运用LabVIEW程序测得SVD处理后的定子电流,得到处理后的定子电流的总谐波失真。各工况下的总谐波失真值如图14所示。
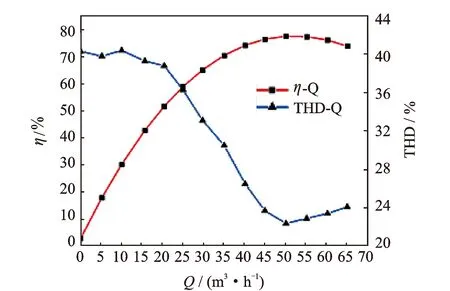
图14 消除电网工频后不同工况下定子电流THD值Fig.14 THD of the current at the operation point after elimination of power frequency
结合图4、图9及图14分析可知,当离心泵运行在小流量(0~20 m3/h)时,离心泵运行效率低,扬程随着流量的增加而增加,此时对应的定子电流的THD较大。小流量时离心泵内部流动的不稳定性较强,水力矩脉动也较大,导致了轴端扭矩的波动较为强烈,反映在定子电流中为THD较大,但是小流量时THD随流量变化不敏感。随着流量从20 m3/h增加到设计流量附近时,定子电流的THD减小,因为随着流量的增加水力矩脉动减弱,泵内部流动趋于稳定。当离心泵运行在高效区(45~55 m3/h),水力矩脉动较弱,泵内部流动较为稳定,定子电流THD较低。可见,定子电流的总谐波失真在一定程度上可以反映离心泵内部流动的稳定性。
4 结束语
基于CFD数值模拟和理论分析了不同工况下离心泵的水力负载转矩特征及其在电机定子电流上的响应。搭建了试验台,借助于霍尔电流传感器及虚拟仪器技术,测得离心泵在不同运行工况下电机定子电流并对其特征进行了分析。离心泵运行状态改变会引起水力负载转矩的变化,最终通过转子轴系传递到电机定子电流中。分析定子电流特征可实现离心泵运行工况的监测。定子电流均方根与离心泵水力矩随着流量的变化有着相似的变化趋势,可用定子电流均方根实现工况监测。水力矩脉动的频率和强度会以信号调制的方式反映在定子电流中。通过SVD分解可实现消除电网工频提取弱信号的目的。消除电网工频后的定子电流THD值可为离心泵运行工况和内部流动状态识别提供参考依据。
