动静干涉下低压涡轮非定常气动载荷研究*
2020-12-08杨成浩冯和英彭叶辉李鸿光
杨成浩, 冯和英, 彭叶辉, 李鸿光,3
(1.湖南科技大学机械设备健康维护湖南省重点实验室 湘潭,411201)
(2.湖南科技大学数学与计算科学学院 湘潭,411201)
(3.上海交通大学机械系统与振动国家重点实验室 上海,200240)
引 言
随着航空叶轮机械的飞速发展,为了减轻涡轮的质量和追求更高的经济性,设计人员在减少涡轮级叶片数量的同时更倾向于将涡轮设计得更加紧凑[1-2],这样能减小发动机尺寸,降低发动机质量,但是轴向间距的变化必然会导致涡轮级间的尾迹、激波等非定常激励发生明显变化[3]。这种气动激励会使涡轮叶片承受由流体诱发的极大的非定常气动载荷,是叶片产生高周疲劳的主要振动源,会直接影响叶片的疲劳强度[4-7]。因此,开展动静干涉下非定常气动载荷控制方法的研究,对于改善涡轮叶片的疲劳强度和可靠性具有重要意义。
涡轮轴向间距对于非定常气动载荷的影响重大。文献[8-9]研究表明,动静干涉产生的扰动波对下游的非定常作用与动静叶间的距离有很大关系。Dring等[10]研究表明,当某型涡轮轴向间距为15%动叶轴向弦长时,尾迹对动叶前缘的非定常压力脉动可达相对动压的80%,其在叶片表面上会产生极大的非定常载荷,严重影响叶轮机的性能和叶片强度等。对于传统的涡轮,Doorly等[11]认为,当轴向间距超过5%静叶弦长时,尾迹在动静干涉中将起主导作用。王仲奇等[12]通过数值仿真的方法对吸附式压气机轴向间距进行了研究,发现轴向间距缩短后,转子与静子之间的非定常干涉加强,压力波动幅值增加,尾迹亏损加剧。文献[13-16]研究了不同轴向间距下气动阻尼的变化,总结了动静干涉作用对叶片非定常压力的影响规律。焦峻峰等[17]研究发现,随着轴向间距的减小,叶排间的非定常性增强,对下游动叶的影响主要体现在前端部分。杨文军等[18]数值仿真表明,叶片表面非定常压力脉动的主要影响因素为相邻叶片排的尾迹扰动。
随着人们对仿生学的深入认识,仿生结构被越来越广泛地应用于航空叶片的结构设计中,而上游静叶结构的微小改变对下游动叶表面所受非定常气动载荷的影响不容忽视。仝帆等[19]研究发现,模仿猫头鹰的尾缘锯齿结构可以显著降低叶片表面的压力脉动幅值,尾缘附近压力脉动幅值最多可降50%左右。文献[20-21]认为,锯齿尾缘可以将尾缘处的展向涡结构进行破碎,大涡变成小涡,从而降低下游叶片的非定常压力脉动,反映到噪声频谱中就是降低动静干涉噪声。Wechmuller等[22]研究发现,尾缘锯齿可以降低尾迹速度亏损,使尾迹沿径向方向发生相位偏移,与下游转子前缘产生破坏性干涉效应,进而降低下游动叶所受的非定常压力脉动。
综上可知,涡轮轴向间距的变化、上游静叶的微改型都会对下游叶片表面的非定常气动载荷产生极大的影响,引起一系列的非定常干涉效应,进而影响整个航空发动机的工作性能。为此,笔者以E3低压涡轮最后一级叶片为研究对象,通过数值仿真其内部三维非定常旋转流场,研究了不同轴向间距和尾缘锯齿结构对动叶表面非定常气动载荷的影响规律,从不同角度分析了两种方法对下游叶片非定常气动载荷的控制效果。
1 研究对象及数值计算方法
1.1 研究对象
E3计划是美国国家航空航天局飞机能源效率(aircraft energy efficiency,简称ACEE)项目中的一个主要内容[23],该项目发动机属于典型的大涵道比民用涡扇发动机。笔者选取美国普惠公司PW-E3低压涡轮最后一级叶片作为研究对象,为降低计算难度,根据文献[17]的方法,对计算区域进行了约化,将静叶、动叶都调整为120,按照1∶1通道建立几何模型,其详细几何参数见表1。
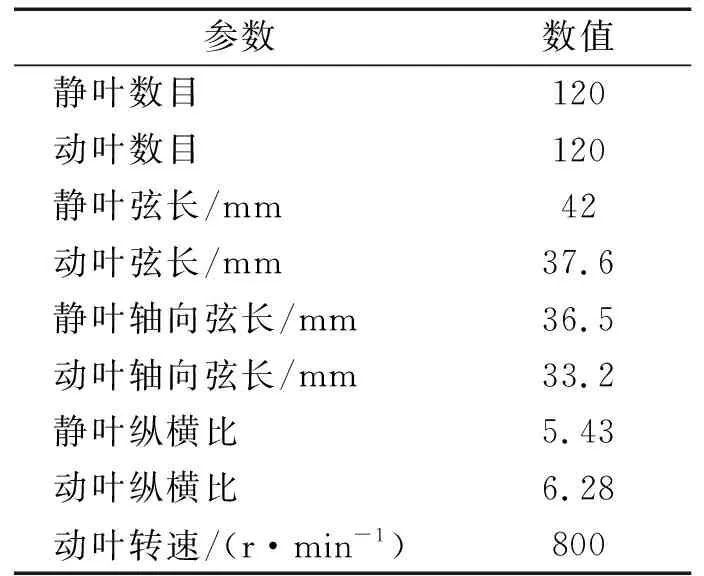
表1 涡轮几何参数Tab.1 Turbine geometry parameters
笔者所考虑的几种物理模型及其级间轴向间距参数如表2所示。静叶所采用的锯齿尾缘结构及其参数如图1所示,其中:C为叶片弦长;H为锯齿高度,H=2Xr;W为锯齿宽度;Z为叶片展向高度;b为叶片尾缘钝度;ε为锯齿顶角。表2中方案1~方案4的物理模型中的静叶叶片均为原型直尾缘叶片,其级间轴向间距分别为40%,50%,60%和70%静叶弦长。方案S所表示物理模型中的静叶叶片则为锯齿尾缘叶片。为便于比较,方案S的轴向间距选为40%静叶弦长,与方案1相同。
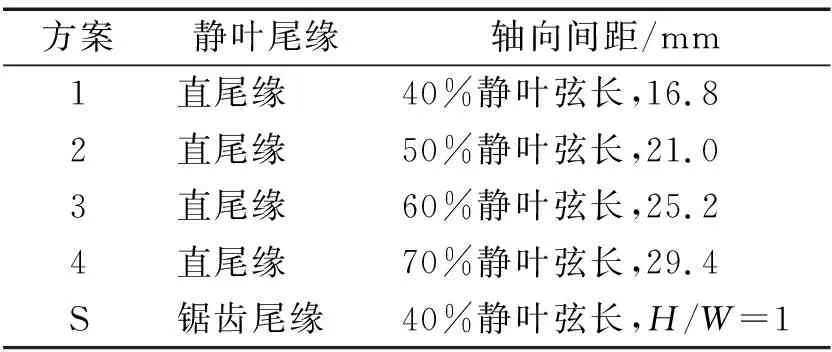
表2 模型方案Tab.2 Physical model scheme
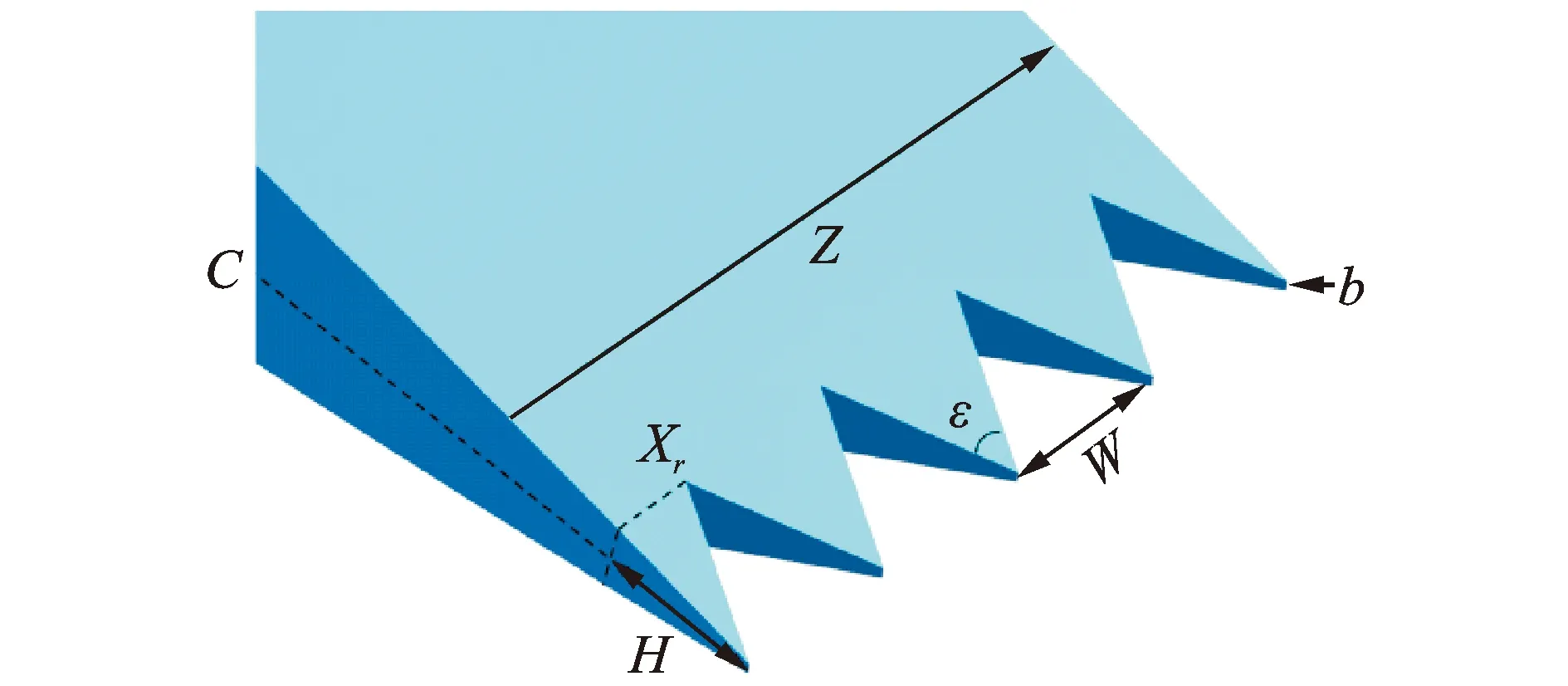
图1 尾缘锯齿的结构参数Fig.1 Structural parameters of trailing edge serrations
1.2 数值计算方法
计算域及网格设置如图2所示,其中:x,y,z方向分别为轴向、展向和径向。计算域入口边界距叶片前缘1.5Cx(Cx为静叶轴向弦长),给定总温、总压、来流湍流度及气流角;出口边界距叶片尾缘3.0Cx,给定静压出口,壁面采用无滑移边界,周向方向采用旋转周期性边界条件。定常、非定常计算分别采用了多重参考系方法(moving reference frame,简称MRF)和滑移网格方法(sliding mesh,简称SM)。
网格划分由ICEM软件完成,为保证网格质量,采用了全六面体结构网格,动静叶均采用H-O-H的拓扑结构:在进口、出口区域和叶栅通道内采用H型网格;在叶片周围采用O型网格。第1层网格高度为0.001mm,网格增长率为1.1。整体网格保证了叶片壁面、轮毂和机匣壁面上的y+<1。
1.3 网格无关性验证
为了排除网格数对数值仿真结果的影响,准备了4套网格(网格数分别为350万、480万、600万和730万)。图3对比了不同网格数下非定常计算得到的方案1涡轮级时均效率,由图可知,当网格数小于600万时,涡轮级的效率随着网格的增加而增加,但网格数从600万增加到730万时,涡轮级效率不再变化,因此对方案1模型而言,600万网格已经符合网格无关性要求。按照同样的方法对方案2、方案3、方案4和方案S进行网格无关性验证,最终这些物理模型的网格数分别选取为630万、654万、670万和710万。
1.4 数值方法可靠性验证
为了验证本研究采用的数值方法的计算精度和可靠性,根据文献[24]中的实验条件对翼型Aerospatiale-A进行了仿真,获得了该翼型在马赫数Ma=0.15、攻角α=13.1°时的压力系数值,并与文献中的实验值进行比较,如图4所示。其中:横坐标为翼型的相对弦长(C为翼型弦长),纵坐标为翼型表面压力系数,两者都为无量纲量。图中压力系数的定义为
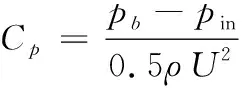
(1)
其中:pb为翼型表面的压力;pin为进口压力;ρ为空气密度;U为来流速度。
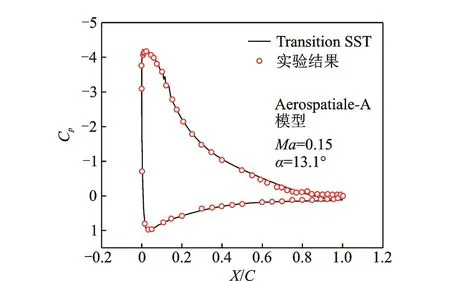
图4 Aerospatiale-A翼型压力系数仿真值与实验值的比较Fig.4 Comparison of pressure coefficient between simulation results and experiment results for Aerospatiale-A airfoil
仿真值和实验值沿翼型弦长方向整体吻合程度较高,表明笔者采用的数值仿真方法具有较高的可靠度。
2 计算结果与分析
非定常计算以收敛的定常结果作为初始值,取转子扫过10个通道为1个周期,其时间步长为3.125×10-5,每周期推进200个物理时间步,计算若干个周期后监测的压力呈现稳定周期性,即达到收敛,然后对非定常流场的结果进行统计分析。
2.1 型面气动载荷分布
对某一时刻叶片表面的压强进行积分可以得到气动激振力,即
F(t)=∮ΩP(t)ds
(2)
其中:Ω为沿着整个叶片外表面的矢量积分;P(t)为t时刻叶片的气动压强分布。
由于动叶外表面恒定不变,因此其表面压强P(t)的变化可以反映动叶表面所受到的气动载荷的变化。
图5描述了不同轴向间距下动叶的10%,50%和90%叶高截面的气动压强分布情况,横坐标为叶片的相对弦长(C为动叶弦长),纵坐标为动叶表面气动压强。由图5可知:①吸力面前缘最低压强随着轴向间距的增加而提高,这使得前缘的逆压梯度降低,吸力面载荷沿弦长方向的分布变得更加均匀,压力面的载荷值则随着轴向间距的增加而降低,因此,轴向间距的增加有利于减小下游叶片表面的气动载荷;②压力面和吸力面之间的压差也随着轴向间距的增加而降低,这有利于降低横向压力梯度,减弱横向二次流,改善能量损失沿叶高的分布,因此,轴向间距的增加有利于改善涡轮的性能;③当上游静叶采用锯齿尾缘结构时,即使轴向间距只有40%静叶弦长,其对下游动叶吸力面前缘最低压强、吸力面载荷沿弦长方向的分布、压力面的有效载荷值、压力面和吸力面之间压差的控制效果都较直尾缘静叶+70%静叶弦长间距(方案4)的组合更好。
与方案1相比,方案S模型吸力面最低载荷可提高34.3%,叶片表面的气动载荷减小约10 kPa。因此,上游静叶采用锯齿尾缘结构对下游叶片非定常气动载荷的控制效果较增加轴向间距的方式更好。
图6展示了不同模型的动叶表面最大气动载荷值,同样截取了10%,50%和90%叶高的数据进行分析。由图可知,当上游静叶为直尾缘静叶时,下游动叶表面最大气动载荷随着轴向间距的增加而降低,但这种降低存在极限,当轴向间距由60%静叶弦长增到70%静叶弦长时,最大载荷值几乎不再减小。从图5也可以看出,方案3与方案4模型的表面气动载荷曲线基本重合。由此可预测,对于方案3模型,尾迹与主流之间的掺混已基本完成,轴向气流的不均匀性也已消除,因此再增加间距也无法进一步降低下游叶片的非定常气动载荷。
从图6还可以看出,当静叶采用尾缘锯齿结构时,动叶表面最大气动载荷还有极大的下降空间。方案S模型的表面最大载荷比方案4降低了5 kPa;与方案1相比,更是降低了约10 kPa。因此,静叶尾缘锯齿结构在控制下游叶片非定常气动载荷方面效果十分明显。
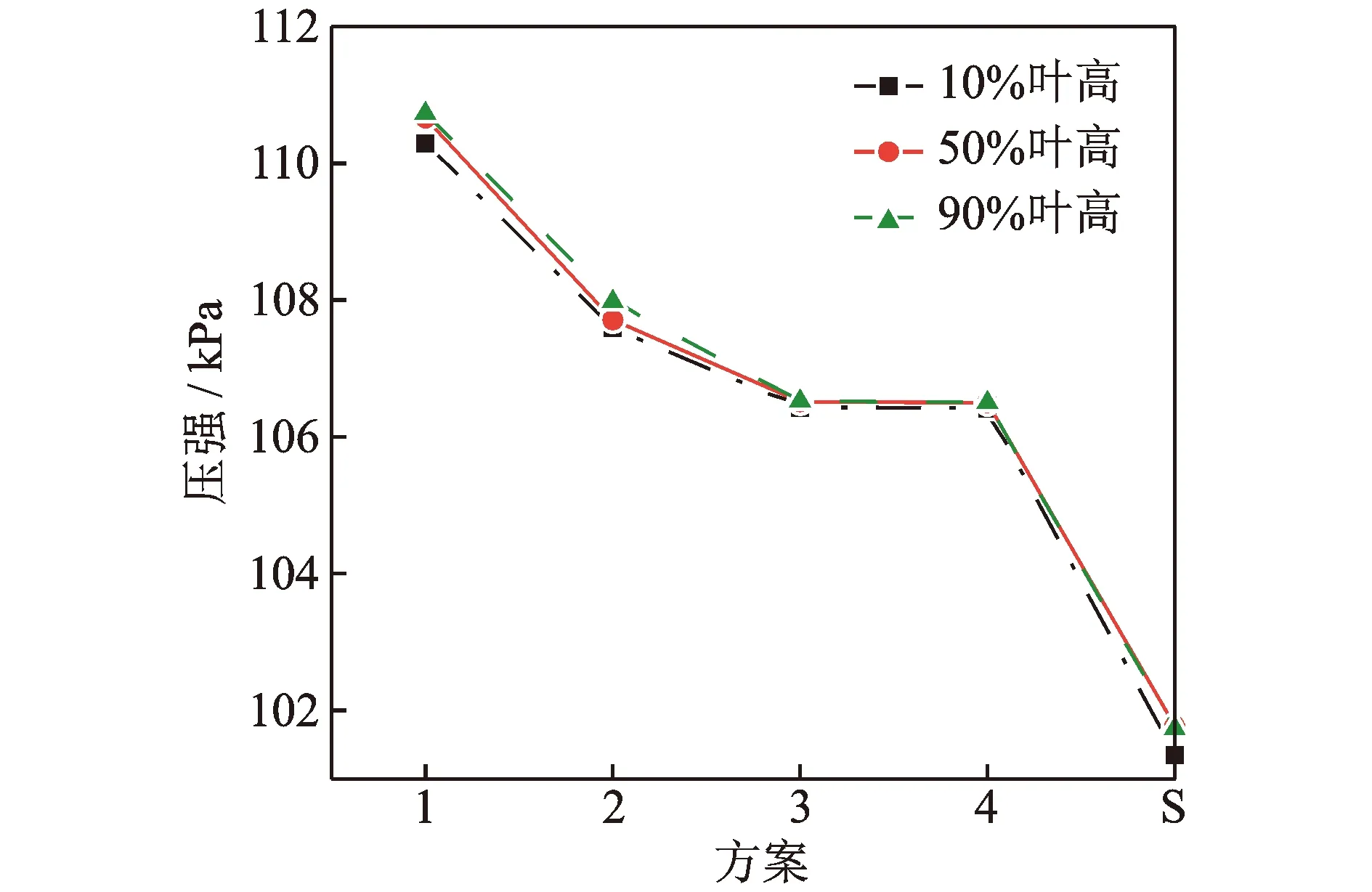
图6 动叶表面最大气动载荷Fig.6 Maximum aerodynamic load on rotor surface
2.2 非定常气动载荷波动
图7显示了1个周期内动叶表面(10%,50%和90%叶高处)气动载荷的波动情况,其中:SS为动叶吸力面;PS为压力面;纵坐标为叶片表面非定常气动载荷波动无量纲幅值。其计算公式为
10lg(Δp/pref)=10lg((pmax-pmin)/2pref)
(3)
其中:pref为参考压力,大小为10-5Pa;pmax和pmin为1个周期内压力的最大值和最小值。
从图7可以看出,3种不同叶高截面处的气动载荷波动在同一轴向间距下的变化规律基本一致。但对于同一截面:①当上游静叶为直尾缘静叶时,动叶表面非定常载荷波动幅值在整个弦长范围内都随着轴向间距的增加而减小,而静叶采用尾缘锯齿结构可以进一步降低动叶表面的气动载荷脉动,与方案1相比,方案S模型的最大载荷波动可降低约30%;②所有模型下的动叶表面载荷波动幅值最大值都发生在距离动静交界面较近的前缘处,这也是上游尾迹对下游叶片非定常干涉影响最大的地方,且轴向距离越小,这种非定常干涉的影响越大;③所有模型下动叶吸力面(SS面)载荷波动从前缘到尾缘都呈正弦状分布,这是尾迹和边界层相互作用的结果[25],而压力面(PS面)载荷波动在整个弦长范围内分布都很均匀,可见上游尾迹对压力面影响较小。
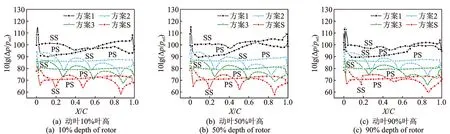
图7 动叶表面气动载荷波动幅值分布Fig.7 Aerodynamic load fluctuation amplitude on rotor surface
上游静叶采用尾缘锯齿结构能显著降低下游动叶表面非定常压力脉动的原因为:尾缘锯齿结构不仅可以加强尾迹与通道内主流的掺混,减少气流的不均匀性,使尾迹对下游动叶的扰动减小,还可以显著改变尾缘处的涡结构,将展向尺度较大的涡破碎成尺度较小的涡,从而降低涡的展向相关性,进而降低非定常压力脉动[20]。
方案1模型下,由于轴向间距较小,尾迹轴向气流来不及调匀就冲击到下游动叶上,形成集中涡系,导致动叶前缘处非定常载荷波动幅值显著上升。在此间距的基础上,上游静叶采用尾缘锯齿结构后(方案S模型),借助锯齿结构对气流的调匀功效及对涡结构的破坏作用,上游尾迹对下游叶片的非定常干涉效应将被极大地削弱。因而,动叶表面的非定常载荷波动也得到了控制。
2.3 非定常气动载荷频谱特性
图8显示了不同模型下动叶表面非定常气动载荷频谱特性。图中横坐标为频率值,纵坐标为功率谱密度。功率谱密度峰值对应的是叶片的通过频率f0及其倍频,其物理意义为单位频带所具有的能量。f0可以表示为
f0=N0n/60
(4)
其中:N0为动叶叶片数;n为动叶转速。
由图8可知:①上游尾迹是下游转子叶片表面气动力的主要激励源,在叶片通过频率的1倍频时占主导地位,高倍频时影响变小;②增加轴向间距有利于降低尾迹对下游叶片表面的非定常干涉作用,如方案1模型时,尾迹还未与主流完全掺混就进入了下游通道,导致动叶表面能量集中,功率谱密度较大,增大轴向间距后,功率谱密度则随之减小;③当静叶采用尾缘锯齿结构后(方案S),尾迹特征得到进一步改善,耗散加快,下游动叶表面边界层的扰动降低,其1倍频和2倍频功率谱密度值均低于所有直尾缘静叶模型。因此,静叶尾缘采用锯齿结构对尾迹干涉效应的控制效果优于增加轴向间距的方式。
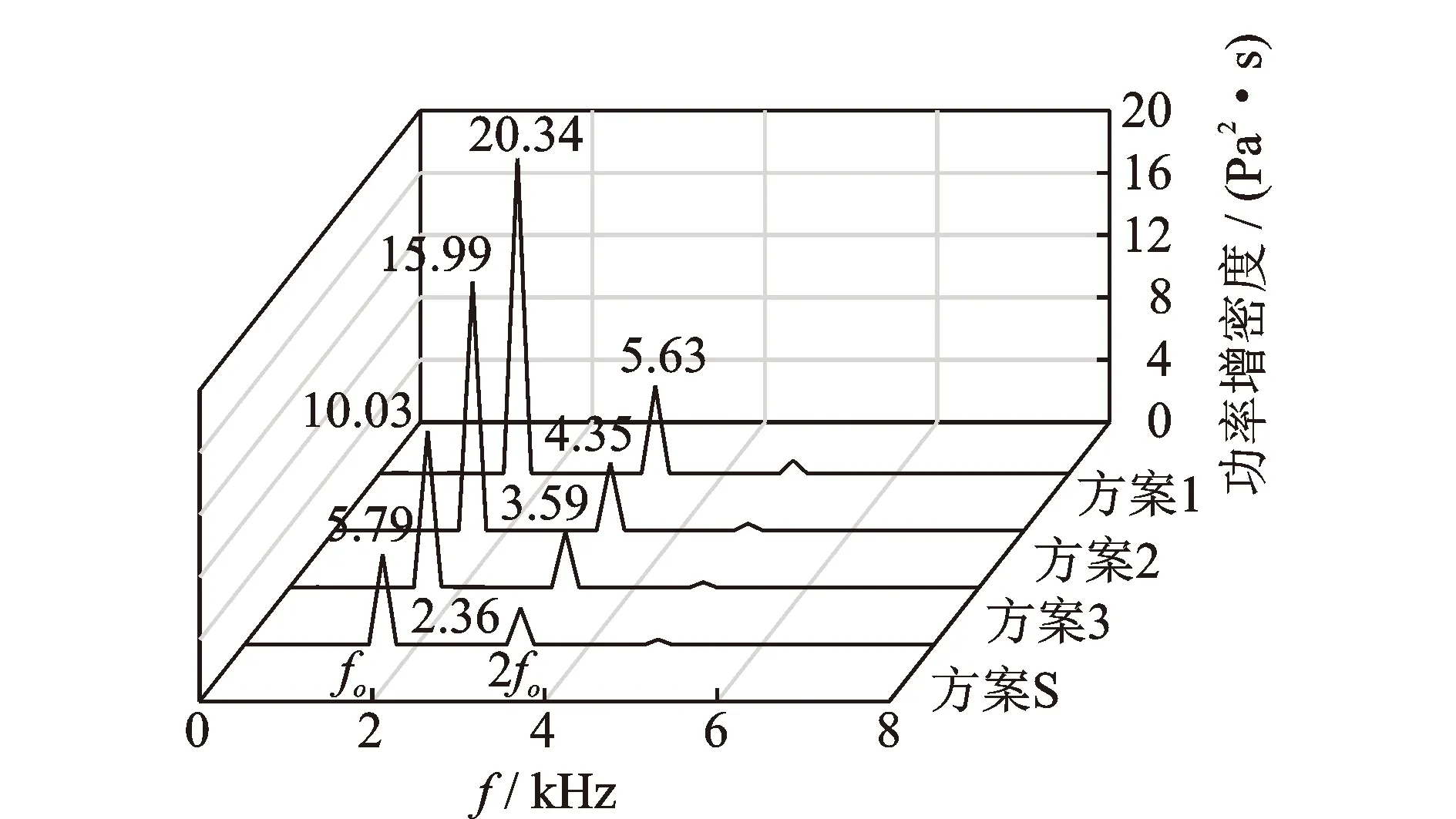
图8 非定常气动载荷频谱分布Fig.8 Frequency distribution of unsteady aerodynamic load
2.4 涡轮级效率分析
图9对比了方案S模型和方案1模型在相同位置处(x=2.5Cx,y=50%叶高)的尾迹型面沿径向的分布。该位置位于方案S模型锯齿尾缘齿根处,因为此展向位置尾迹亏损最大。图中:横坐标z为垂直尾迹的径向方向;SS为吸力面;PS为压力面。由图9可知,在方案1基础上采用尾缘锯齿结构后(方案S),尾迹耗散加快,速度沿径向成振荡分布,且速度亏损明显降低。方案1的速度亏损约为124.6 m/s,而方案S的速度亏损约为48.9 m/s,减少了75.7 m/s。由此可知,当静叶采用尾缘锯齿结构后,极大地加强了尾迹与主流之间的掺混,减少了速度亏损。从图中还可以看出,与原型叶片相比,锯齿尾缘叶片的尾迹沿径向发生了相位偏移,文献[22]也发现了相似的现象。
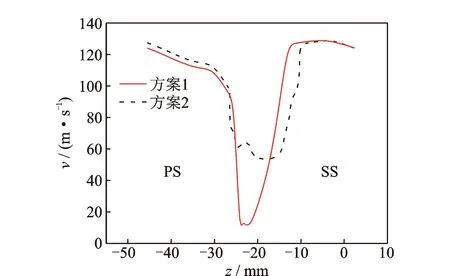
图9 直尾缘与锯齿尾缘相同展向位置处的尾迹型面Fig.9 The cascades of wake profile for straight trailing edge and serrated trailing edge atthe same spanwise location
图10对比了不同模型下低压涡轮的质量流量。由图可知:当上游静叶为直尾缘静叶时(方案1~方案3),轴向间距对质量流量的改善能力有限,增值在1%以内;而当上游静叶采用锯齿尾缘结构后(方案S),质量流量可显著提升。质量流量的提升有利于改善涡轮的流通能力。
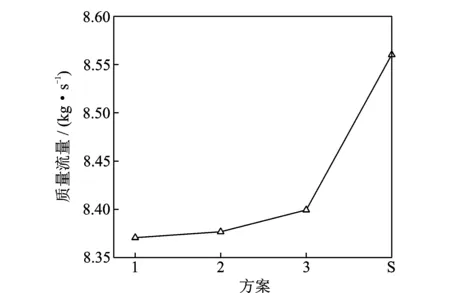
图10 不同模型下涡轮的质量流量Fig.10 The mass flow of turbine under different model scheme
图11显示了不同模型下静叶通道内的总压恢复系数σ和涡轮级时均效率η,σ和η分别表示为
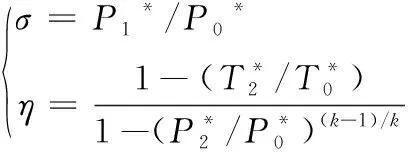
(4)
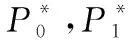
由图11可以看出:①当上游静叶为直尾缘静叶时,涡轮的总压恢复系数和时均效率均随着轴向间距的增大而逐渐提升,轴向间距的增加有利于改善涡轮的气动性能;②当静叶采用尾缘锯齿结构时,涡轮的总压恢复系数能得到进一步的改善。时均效率的提升虽然不明显,但相同轴向间距下,尾缘锯齿静叶涡轮的时均效率比直尾缘静叶略有优势。例如,锯齿尾缘静叶+40%静叶弦长间距(方案S)比直尾缘静叶+40%静叶弦长间距(方案1)的总压恢复系数高0.69%,效率也能提升0.22%,其效率值与方案2模型的涡轮效率相当。因此,在不影响涡轮效率的前提下,采用锯齿尾缘静叶,涡轮轴向间距可比采用直尾缘静叶时缩短10%。
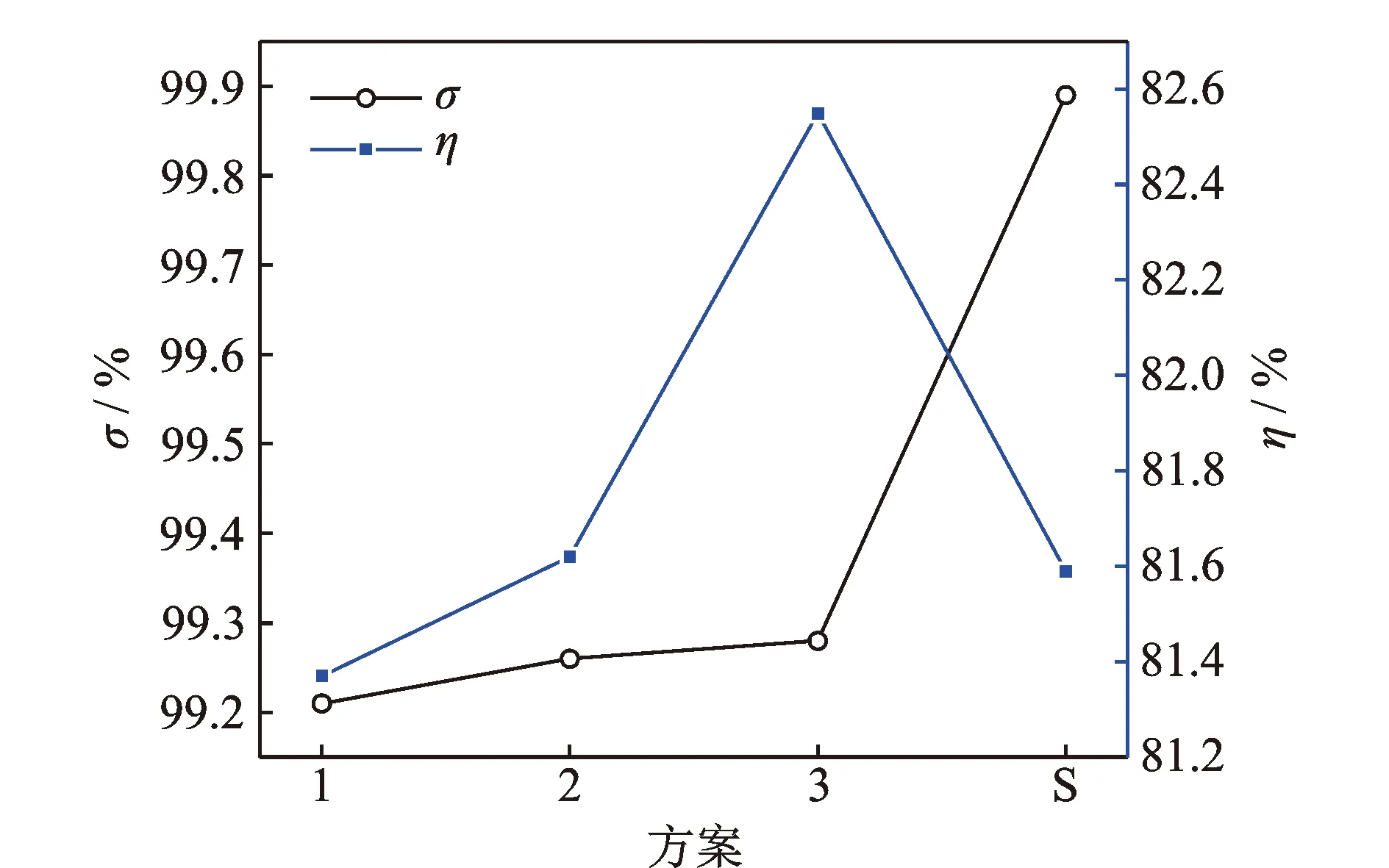
图11 总压恢复系数和时均效率Fig.11 Total pressure recovery coefficient and time-averaged efficiency
3 结 论
1) 当上游静叶为直尾缘静叶时,下游动叶表面的气动载荷及非定常载荷波动幅值都随着轴向间距的增加而减小,而涡轮的流通能力、总压恢复系数及时均效率则随着轴向间距的增加而增大。因此,涡轮的转静干涉效应、气动性能都随着轴向间距的增加而得到改善,但这种单纯的增加轴向间距的方式对涡轮性能的改善能力有限。
2) 静叶采用尾缘锯齿结构则能进一步改善涡轮的转静干涉效应及其气动性能。就所研究的各方面指标而言,方案S模型都明显优于方案4模型。与方案1模型相比,方案S模型更能降低下游动叶表面的气动载荷约10 kPa,减少尾迹速度亏损75.7 m/s。
3) 从整体上来看,锯齿尾缘静叶模型对下游动叶非定常气动载荷的控制效果比仅改变轴向间距方式的效果要好。在涡轮的转静干涉效应、气动性能得到大幅改善且不影响涡轮效率的前提下,采用锯齿尾缘静叶,涡轮轴向间距可比采用直尾缘静叶时缩短10%,这更符合现代航空发动机“更轻的结构、更高的级负荷和更紧凑的级间距”的设计理念。
