两种串列方柱气动性能的试验研究*
2020-12-08杜晓庆陈如意许汉林马文勇
杜晓庆, 陈如意, 许汉林, 马文勇
(1.上海大学土木工程系 上海,200444) (2.上海大学风工程和气动控制研究中心 上海,200444)
(3.石家庄铁道大学风工程研究中心 石家庄,050043)
1 问题的引出
大长细比柱群结构在土木工程、海洋工程、机械工程和航天航空工程等领域有着广泛的应用[1-4],如超高层建筑群、桥梁并列索、海底电缆和热交换器等。柱群之间的流动干扰使得柱群周围的流场变得非常复杂,且与单个柱体有很大差别。因此,柱群绕流问题受到众多学者关注,特别是圆柱和方柱。均匀来流作用下的串列双方柱是简化的柱群绕流模型,研究其气动性能有助于理解柱群之间的干扰机理,并得到较为广泛的研究[5-18]。图1为串列双方柱的两种布置形式。以往研究主要针对水平布置串列双方柱(见图1(a)),尚未见到针对对角布置串列双方柱(见图1(b))的研究。图1中:U为来流速度;B为方柱边长;P为两方柱中心间距;CD,CL分别为阻力系数和升力系数;a(a′) ~d(d′)为方柱各面中点(顶点)。
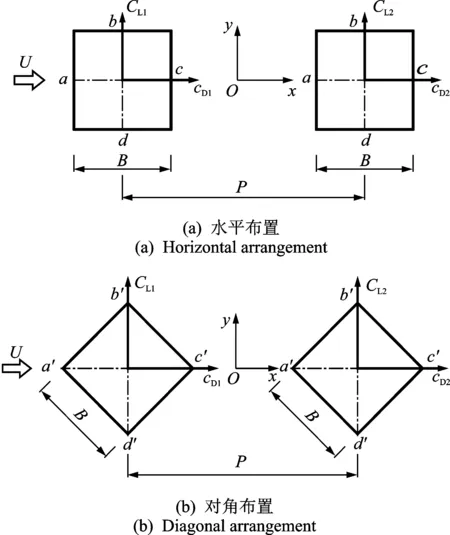
图1 串列双方柱的两种布置形式Fig.1 Two arrangements of two tandem square cylinders
为进一步研究水平布置串列方柱的绕流特征,研究者在低雷诺数下进行了流迹显示试验和数值模拟研究。Yen等[12]利用粒子图像测速试验在Re= 300~1 100时,将不同间距下的水平串列双方柱的流场分为单一钝体、剪切层再附和双涡脱3种流态。Sohankar[13]通过数值模拟在Re= 130,150和500时也得到了类似的流态分类:当Re= 500,在P/B< 1.5时为单一钝体流态,上游方柱尾流产生的旋涡在下游方柱后脱落;在P/B= 1.5 ~ 5.0时为剪切层再附流态,从上游方柱分离的剪切层会再附到下游方柱侧面;在P/B≥ 5.0时为双涡脱流态,在双方柱后侧均有涡脱产生。另外,引起水平串列双方柱流态变化的临界间距会因为雷诺数不同存在一定差异。
方柱的平面布置形式是影响柱群之间气动干扰的因素之一。实际工程中常会出现对角布置双方柱形式,如纽约双子塔。Lam等[14]研究了5个方柱在水平布置和对角布置形式下的气动干扰问题,研究表明两种布置形式的方柱在气动性能方面存在很大差异。因此,有必要对对角布置双方柱进行更为细致的研究,以澄清其干扰条件下的气动性能。
为了掌握两个对角布置串列方柱的气动性能,并比较其与水平串列双方柱的差异,文中以均匀来流作用下的水平串列双方柱和对角串列双方柱为研究对象,在雷诺数Re= 8.0×104时考虑了8种间距比(P/B= 1.75 ~ 5.00)。通过同步测压风洞试验,得到两种布置形式串列双方柱的表面风压。重点研究了对角布置串列方柱的气动力、风压分布和Strouhal数等气动性能随方柱间距的变化规律,并与水平布置串列方柱进行了比较。
2 风洞试验
试验在石家庄铁道大学风工程研究中心的双试验段回流风洞高速段进行,试验段长为5.0 m,宽为2.2 m,高为2.0 m,背景湍流度I≤ 0.2%。试验采用刚性节段模型,模型为120 mm×120 mm×1 620 mm的方柱,采用塑料板材制作,长细比为13.5,方柱两端设置直径为1.0 m的导流端板。串列双方柱采取面对面和角对角两种布置形式,均与来流呈串列布置,分别称为水平串列双方柱和对角串列双方柱,试验模型示意图如图1所示。每个方柱模型上分别布置了4个测压截面,沿每个测压截面周向布置了44个测点,总共布置了352个测压点。
试验采用电子压力扫描阀的采样频率为330 Hz,采样时间约为36 s。试验风速U为10 m·s-1,以方柱边长B为特征尺寸计算得到雷诺数Re约为8.0×104,面积阻塞率约为5%。为了研究两种布置形式串列双方柱的气动性能随间距变化的规律,试验考虑了8种间距比,P/B分别为1.75,2.00,2.50,3.00,3.50,4.00,4.50和5.00。
3 试验结果分析
3.1 气动力系数
3.1.1 平均气动力系数
图2为两种布置形式串列双方柱的平均阻力系数CD(通过对方柱表面风压系数沿其周向积分得到)随间距变化的曲线。为了方便比较,图中也分别给出了文献[15]中水平串列双方柱的数据和本研究的单方柱试验结果。由图可见,水平串列双方柱的平均阻力系数随间距的变化趋势与文献[15]基本一致,但由于试验雷诺数不同,平均阻力系数发生突变的位置不同。另外,文中两种单方柱的平均阻力系数也与文献[19-20]结果吻合良好。在本试验结果中,两种布置形式串列双方柱的平均阻力系数随间距的变化趋势有明显差异;随着间距增大,两种布置形式的上游方柱的平均阻力系数与各自单方柱的平均阻力系数较为接近,而下游方柱的平均阻力系数则远小于单方柱;且两种布置形式的下游方柱的平均阻力系数差异较大,特别是当P/B> 3.00时。
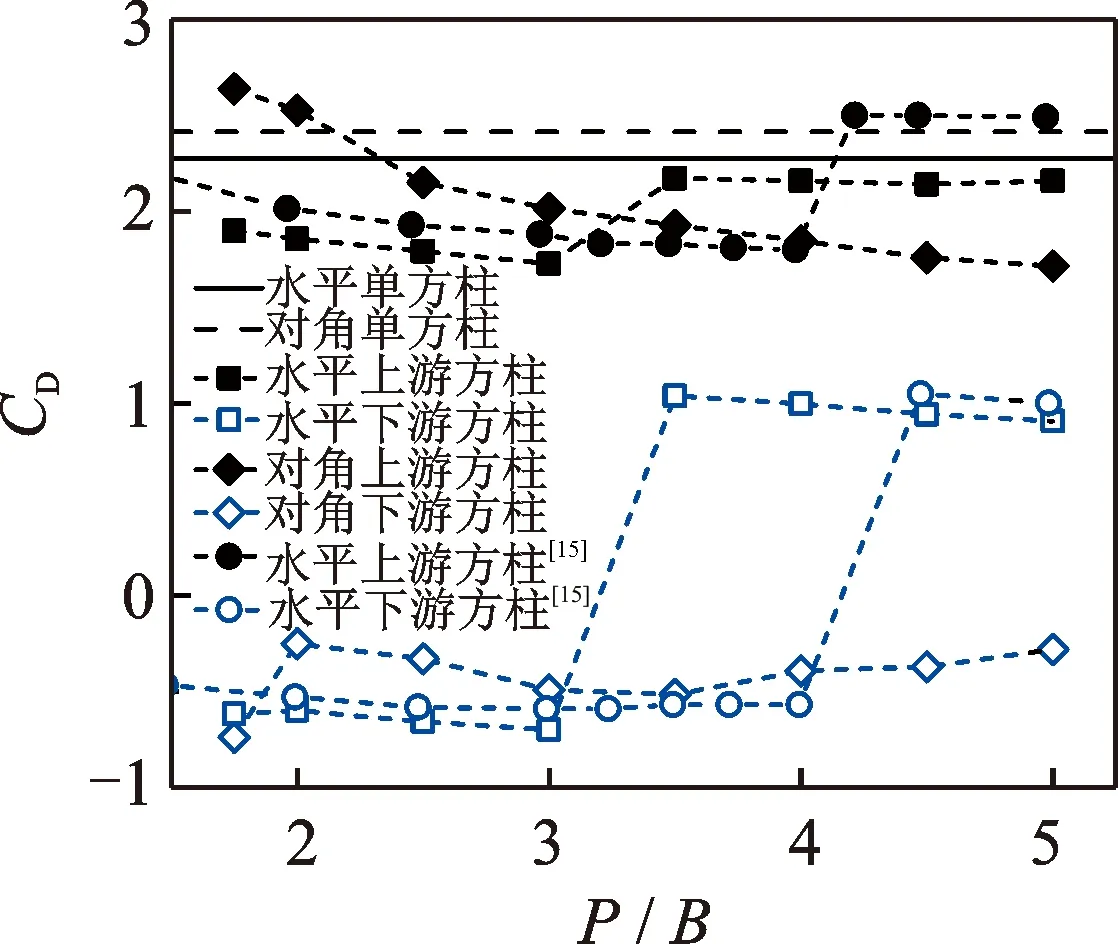
图2 平均阻力系数随间距比的变化Fig.2 Variation of mean drag coefficient with spacing ratio
对于水平串列双方柱,其下游方柱的平均阻力系数在P/B= 3.00 ~ 3.50时发生跳跃现象,数值由负值突变为正值,上游方柱的平均阻力系数在此间距范围内也有明显增大。文献[8,13]中将这种发生气动力跳跃的间距比称为临界间距比。对于对角串列双方柱,其平均阻力系数在试验间距范围内没有发生类似的跳跃现象,其下游方柱的平均阻力系数在文中间距范围内均为负值。值得注意的是,在小间距下(P/B= 1.75和2.00),上游方柱的平均阻力系数会大于单方柱,并随着间距的增加逐渐减小。
临床在不断的研究实践中指出,对于早期急性心肌梗死患者的治疗,关键在于在较短的时间内,快速恢复患者受阻血管的血液供应,积极改善患者的心室功能和心肌功能[6]。目前临床上常用的再灌注治疗手段主要有经皮冠状动脉腔内成形术和静脉溶栓两种,这两种再灌注治疗方式在早期急性心肌梗死患者的治疗中均表现出了较大的临床优势,但是由于经皮冠状动脉腔内成形术在治疗过程中不仅对医疗条件有较高的要求,同时还需考虑到患者的身体是否能够耐受,因此该治疗方式并不适用于大范围进行推广应用[7-8]。
3.1.2 脉动气动力系数
图3为两种布置形式串列双方柱的脉动阻力系数CDf和脉动升力系数CLf(即气动力系数的标准差)随间距变化的曲线,图中也分别给出了水平布置和对角布置的单方柱的试验结果。
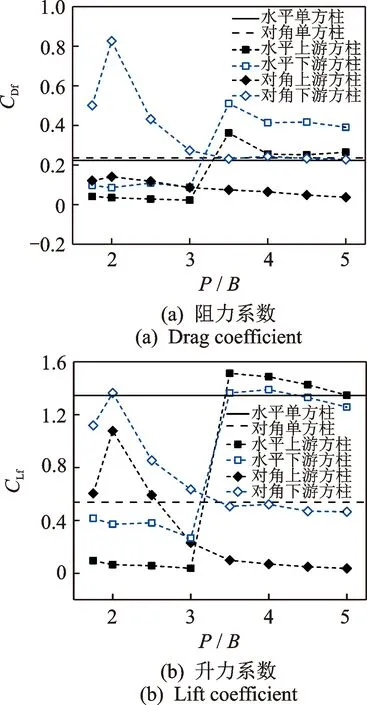
图3 脉动气动力系数随间距比的变化Fig.3 Variation of fluctuating aerodynamic coefficients with spacing ratio
对于水平串列双方柱,可以看到,无论是脉动阻力还是脉动升力,在临界间距前后均会发生跳跃现象。根据文献[12]的研究,这种气动力的跳跃现象与流态变化有关,在临界间距前后,双方柱的流态分别为剪切层再附流态和双涡脱流态。从图中可知,上、下游方柱的脉动气动力系数随间距的变化趋势一致,在临界间距前,上、下游方柱的脉动阻力和脉动升力系数均小于单方柱,且下游方柱大于上游方柱;在临界间距后,上、下游方柱的脉动力都接近于单方柱,下游方柱的脉动阻力仍大于上游方柱,但其脉动升力则小于上游方柱。
对于对角串列双方柱,其脉动气动力随间距增大也有很大波动,但其变化情况较水平串列双方柱有很大差异。在小间距(P/B= 1.75 ~ 3.00)下,下游方柱的脉动阻力和脉动升力很大,不仅大于单方柱的数值,同时也远大于水平串列双方柱,而上游方柱仅脉动升力大于单方柱,其脉动阻力随间距变化较小;在较大间距(P/B= 3.00 ~ 5.00)下,上、下游方柱脉动气动力系数远小于水平串列双方柱,其中下游方柱的脉动气动力接近于单方柱。
3.2 表面风压系数
3.2.1 平均风压系数
图4和图5分别为两种布置形式串列双方柱的平均风压系数CP分布曲线。由图可见,两种布置形式的串列双方柱的表面平均风压分布明显不同,其上、下游方柱的风压分布与各自的单方柱相比也均有明显差异,而下游方柱的差别更大。
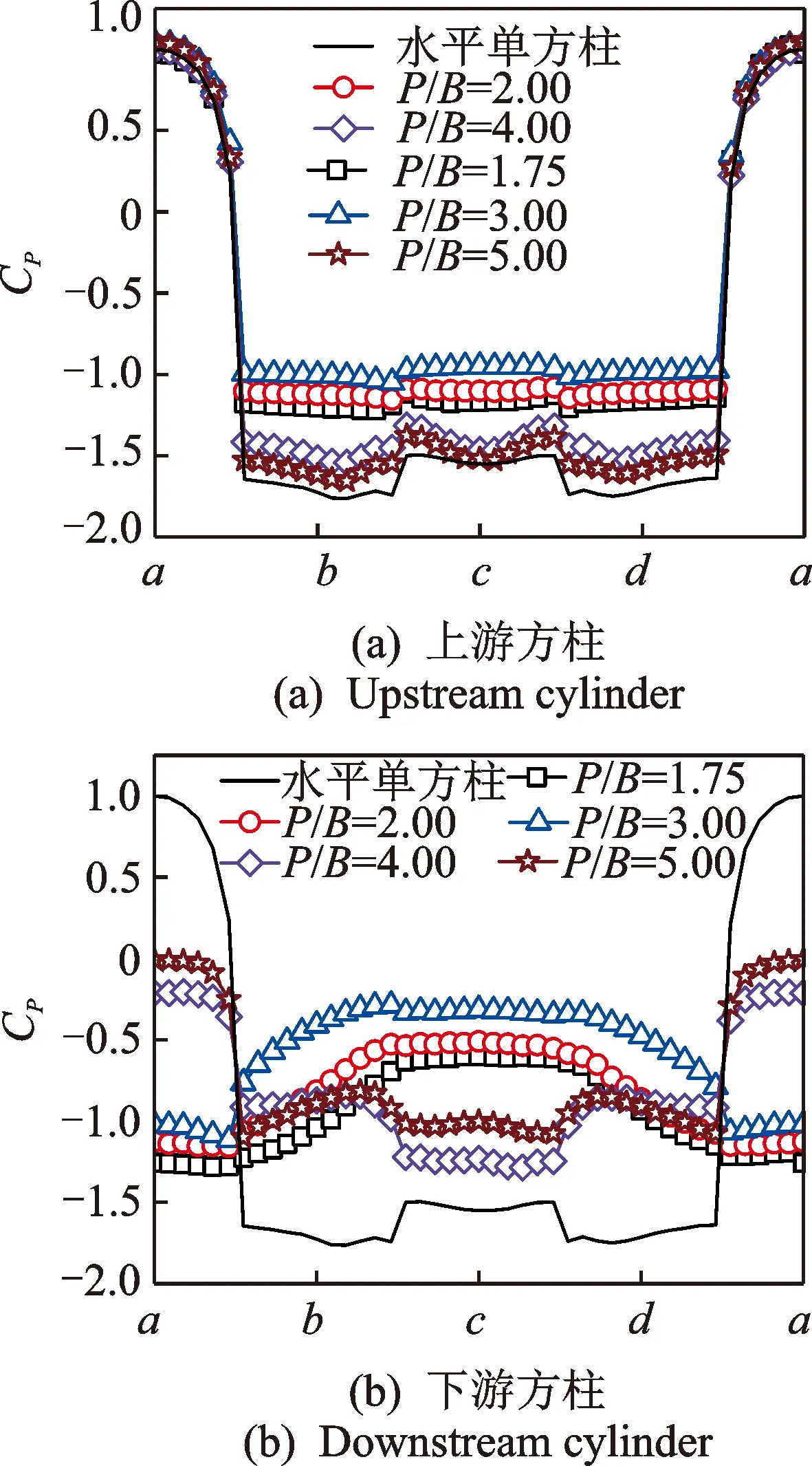
图4 水平串列方柱平均风压分布Fig.4 Mean pressure distribution of horizontal tandem square cylinders
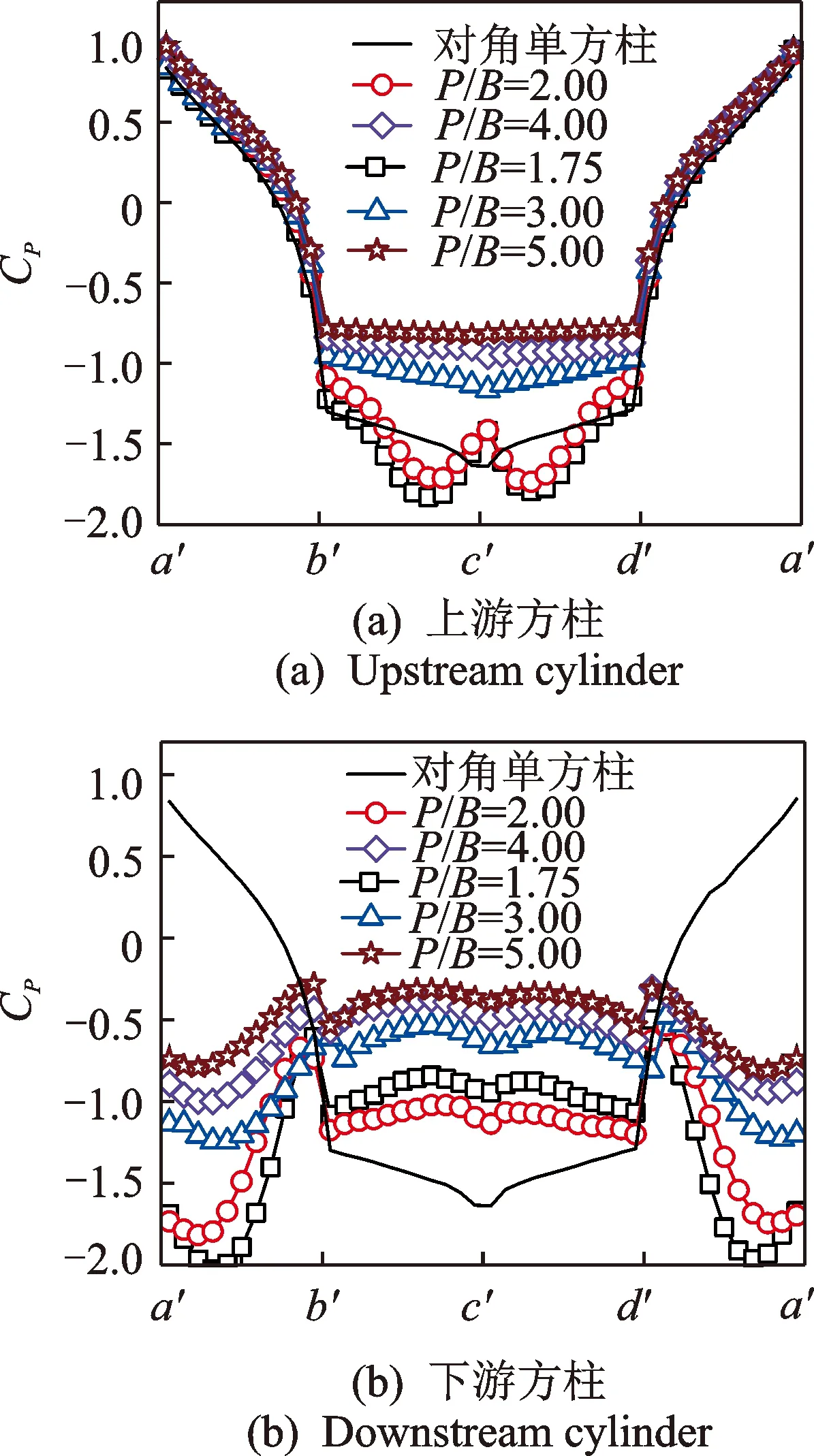
图5 对角串列方柱平均风压分布Fig.5 Mean pressure distribution of diagonal tandem square cylinders
对于水平串列双方柱,其临界间距比前后的风压分布形态有显著差异。当P/B= 1.75 ~ 3.00时,下游方柱的迎风面受到很强的负压,当间距增大后负压强度减弱;随着间距增大,上游方柱的风压分布逐渐接近于单方柱,特别是大于临界间距的工况(P/B= 4.00 ~ 5.00)。另外,注意到间距比为3和4的两种工况的风压分布有明显的不同,在气动力上表现为临界间距前后气动力系数的突变。
对于对角串列双方柱,间距比为P/B= 1.75 ~ 2.00和P/B= 3.00 ~ 5.00的风压分布形态明显不同。对于上游方柱,P/B=1.75 ~ 2.00时的背风面(b' ~d')负压强度远远大于间距比为P/B= 3.00 ~ 5.00时的数值,同时也大于单方柱和相同间距下的水平上游方柱;对于下游方柱,P/B= 1.75 ~ 2.00时的迎风面(a' ~b',d' ~a')负压强度也明显大于P/B= 3.00 ~ 5.00时和相同间距下水平下游方柱的数值;另外,下游方柱表面风压在所有间距下均为负压,且迎风面的负压强度总体上大于背风面,因而下游方柱始终受到负阻力的作用。
3.2.2 脉动风压系数
图6和图7分别为两种布置形式串列双方柱的脉动风压系数CPf(即风压系数标准差)分布曲线。由图可见,两种布置形式的串列双方柱的脉动风压分布形态随着间距的增大均变化剧烈,但变化趋势截然不同。
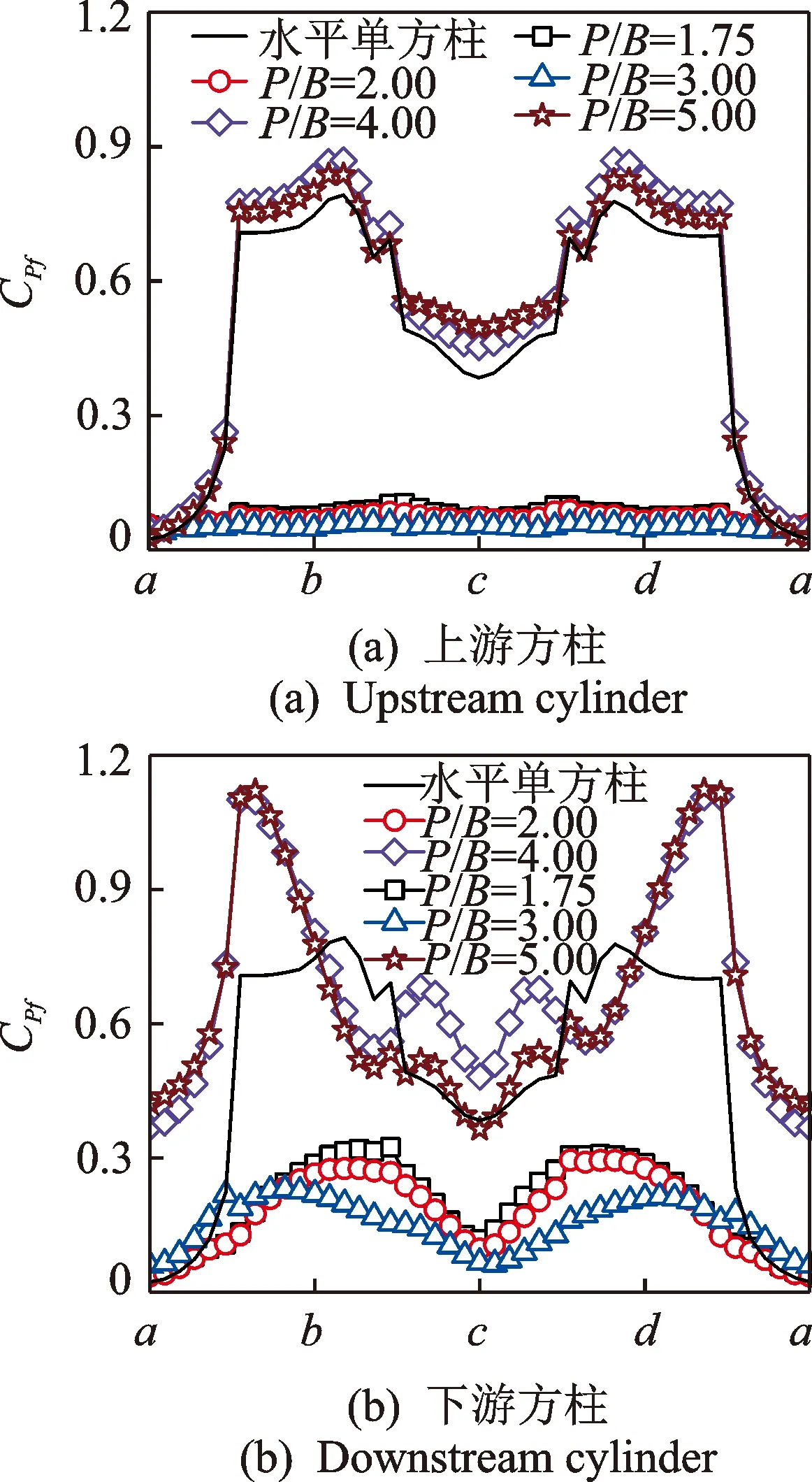
图6 水平串列方柱脉动风压分布Fig.6 Fluctuating pressure distribution of two tandem square cylinders in horizontal arrangement
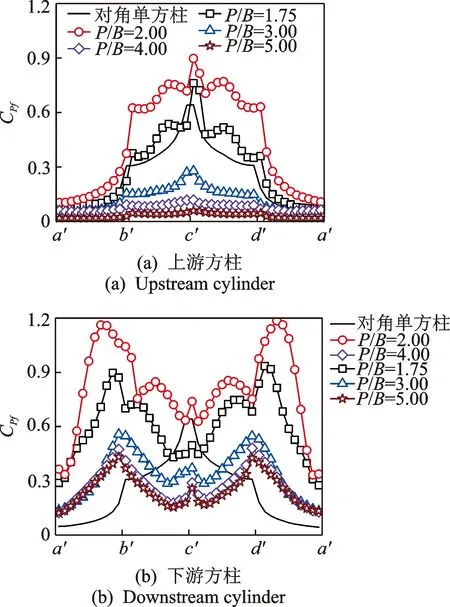
图7 对角串列方柱脉动风压分布Fig.7 Fluctuating pressure distribution of two tandem square cylinders in diagonal arrangement
对于水平串列双方柱,上、下游方柱的脉动风压系数在临界间距前后有显著差异。P/B= 1.75 ~ 3.00时,上、下游方柱的脉动风压较小,且远低于单方柱;P/B= 4.00 ~ 5.00时,上游方柱的脉动风压在侧面和背风面略大于单方柱,而下游方柱迎风面和侧面的脉动风压则远远大于单方柱,特别是在迎风面的两角点附近,这可能是由于双涡脱流态时上游方柱尾流中的旋涡与下游方柱的迎风面发生撞击造成的。
对于对角串列双方柱,间距比为P/B= 1.75 ~ 2.00和P/B= 3.00~ 5.00时,上、下游方柱的脉动风压差别很大。对于上游方柱,P/B= 1.75 ~ 2.00时其背风面(b' ~d')的脉动风压远远大于间距比为P/B= 3.00 ~ 5.00时的脉动风压,也大于单方柱和相同间距下的水平上游方柱;对于下游方柱,P/B= 1.75 ~ 2.00时方柱整体的脉动风压较大,同时大于P/B= 3.00 ~ 5.00时的数值,以及单方柱和相同间距下水平下游方柱的脉动风压,尤其在迎风面前角点处(即b'点和d'点),最大脉动风压系数达到1.2左右。
3.3 Strouhal数及升力功率谱
图8和图9分别为两种布置形式下游方柱的升力功率谱(power spectrum density,简称为PSD),其峰值所对应的折算频率即为Strouhal数(St=fB/U,其中f为涡脱频率)。对于两种布置形式的串列双方柱,其上、下游方柱的升力功率谱均出现明显的峰值,且随间距变化的趋势一致,上游方柱的峰值变化幅度明显大于下游方柱,而上、下游方柱的功率谱中峰值所对应的St数基本相同。
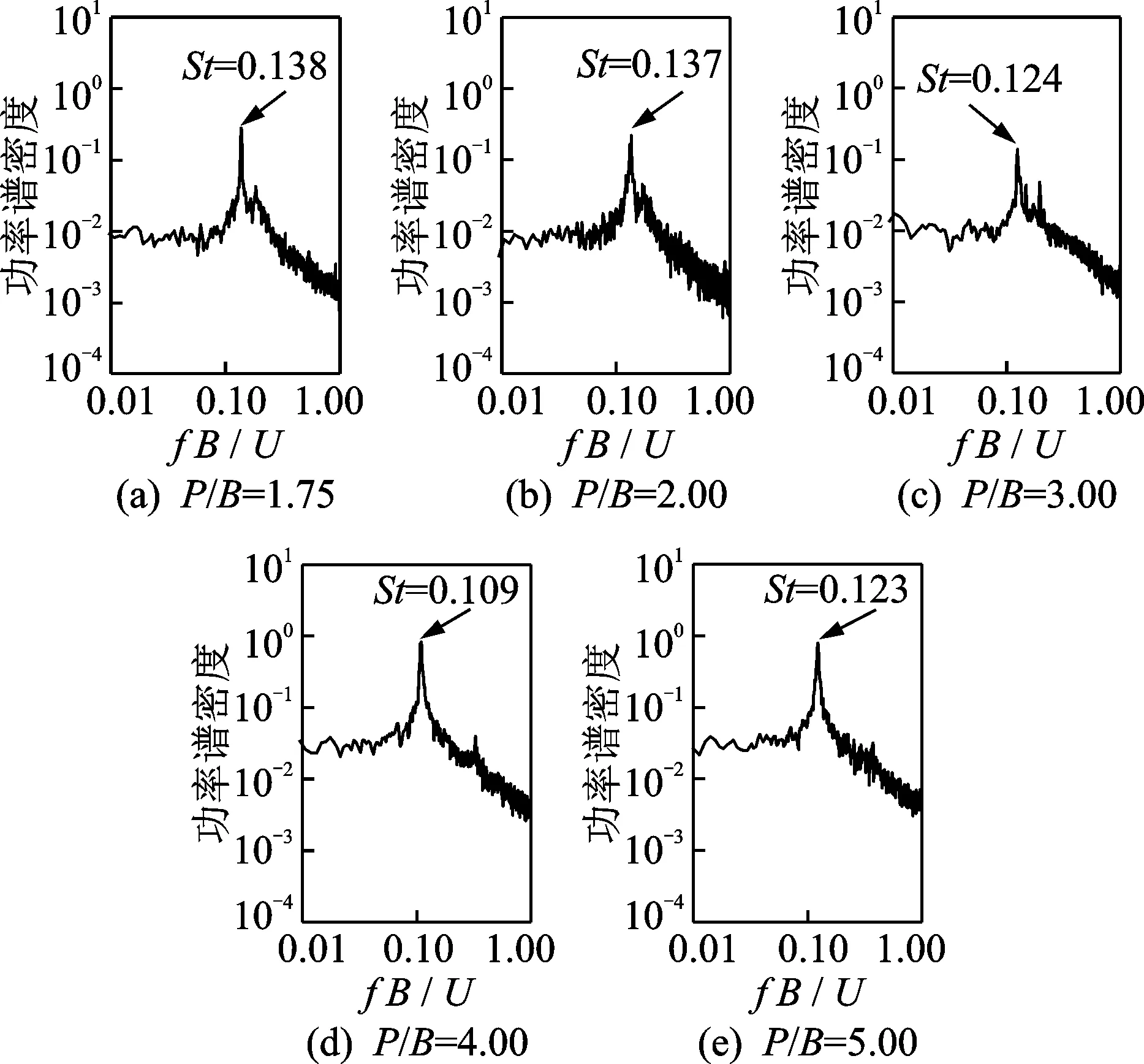
图8 水平串列方柱的下游方柱升力功率谱Fig.8 Lift power spectra of the downstream cylinder of horizontal tandem square cylinders
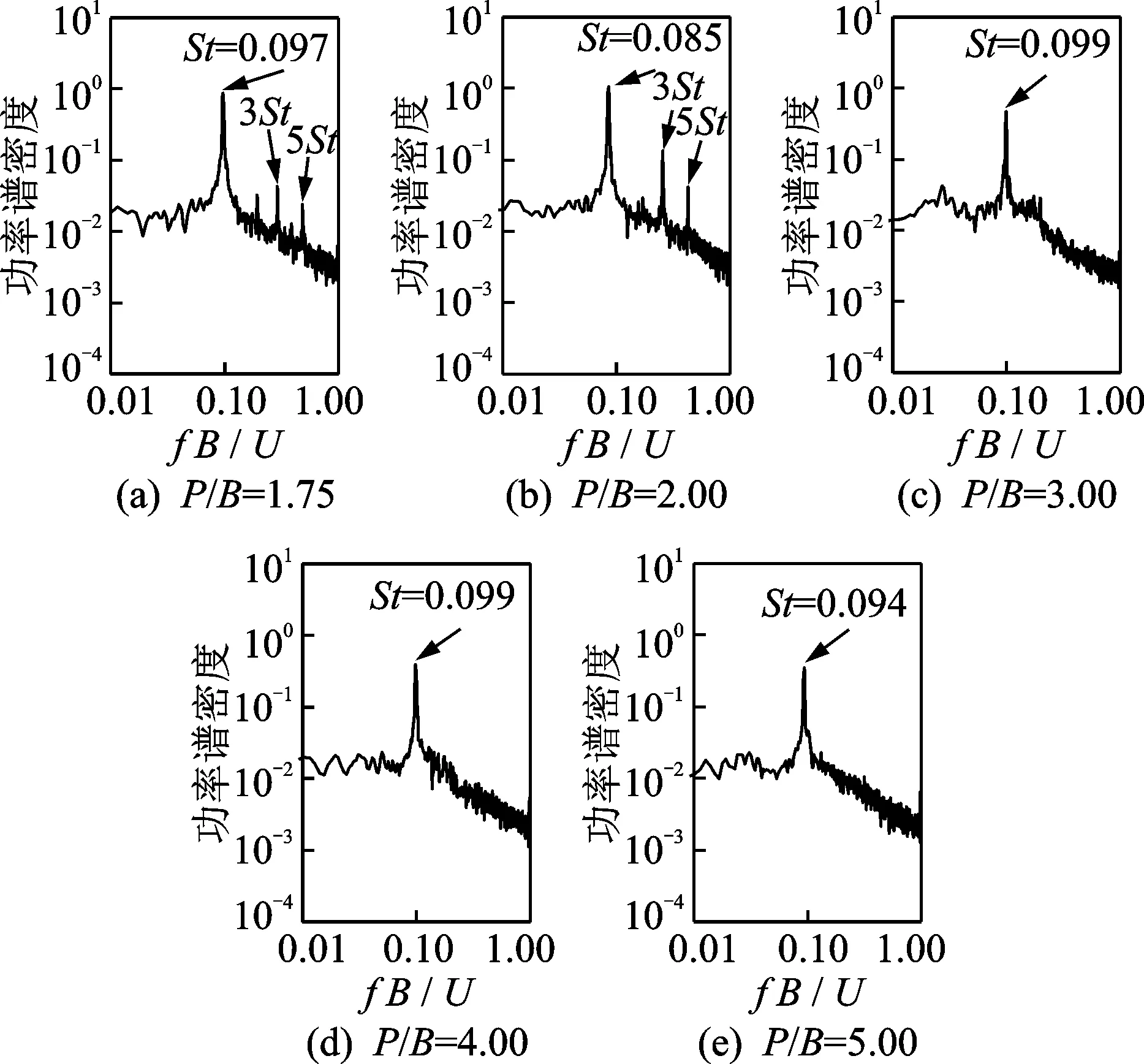
图9 对角串列方柱的下游方柱升力功率谱Fig.9 Lift power spectra of the downstream cylinder of diagonal tandem square cylinders
对于水平串列双方柱,在临界间距前,功率谱峰值随间距增加而降低;在临界间距后突然增大。对于对角串列双方柱,在试验间距范围内,功率谱峰值整体随间距的增加而减小,仅在P/B= 2.00时会突然增大;较为特殊的是,在小间距下(P/B< 3.00)功率谱中均会出现多个峰值,折算频率分别为3St和5St,其原因尚不清楚。此外,从总体上看,水平串列双方柱的St数在临界间距前随间距增大而减小,在临界间距后随间距增大而增大,并逐渐接近于单方柱的St数。对于对角串列双方柱,其St数明显小于相同间距下的水平串列双方柱,且随着间距比从1.75增大至5.00,其数值变化较小。
4 结 论
1) 对于水平串列双方柱,下游方柱的气动力在P/B= 3.00 ~ 3.50时会发生跳跃现象,其平均阻力会由负值突变为正值。对于对角串列双方柱,其下游方柱的平均阻力系数则在文中的间距范围内均为负值,上游方柱的平均阻力系数在小间距(P/B= 1.75和2.00)时会大于单方柱。
2) 从整体上看,两种串列双方柱的气动力和风压分布在间距比P/B= 3.00前后差异较大。当间距比P/B< 3.00时,对角布置上、下游方柱的整体气动力和风压(包括平均和脉动)分别大于水平布置的上、下游方柱;而当P/B> 3.00时则情况相反。
3) 对角串列双方柱的St数明显小于相同间距下的水平串列双方柱,且当P/B< 3.00时,对角串列双方柱的升力功率谱会出现多个峰值,而水平串列双方柱在本研究间距范围内均只有一个峰值。
