强化学习长短时记忆神经网络用于状态预测*
2020-12-08汤宝平王家序
李 锋, 陈 勇, 汤宝平, 王家序, 3
(1. 四川大学机械工程学院 成都, 610065) (2. 重庆大学机械传动国家重点实验室 重庆, 400044)
(3. 四川大学空天科学与工程学院 成都, 610065)
引 言
旋转机械广泛应用于各种关键的设备中,其性能状态直接决定着设备能否长期安全可靠地运行[1]。由于目前对许多旋转机械建立物理失效预测模型十分困难[2],基于数据驱动的状态预测方法获得了越来越多的关注和研究。基于数据驱动的状态退化趋势预测方法一般分为:现代模型预测方法(例如灰色模型(grey model,简称GM)),数值分析预测方法(例如最小二乘支持向量机(least squares support vector machine,简称LSSVM)等)和人工智能预测方法(例如专家系统和神经网络等)。文献[3]采用小波GM开发了一种用来预测旋转机械故障的分析仪。文献[4]在时序数据的特征空间上将预测当做高斯过程,利用贝叶斯预测模型(Bayesian prediction model,简称BPM)进行风力发电机组轴承失效预测。文献[5]利用模糊神经网络对轴承进行剩余寿命预测。然而,以上预测方法仍存在很多缺陷。对于GM,驱动变量之间的互相作用关系不明确,未考虑在作用期内驱动变量对系统行为序列的作用强度随时间变化的问题,使得GM很难得到精确的预测结果。由于BPM通常无法及时找到最需要推理的因素,不能及时得到该因素的预测值。传统神经网络如LSTMNN和循环神经网络(recurrent neural network,简称RNN)的隐层层数和隐层节点数的选择没有完善的理论指导[6],一般只能靠经验选择,导致神经网络的预测精度和计算效率都不佳。作为一种解决序贯决策问题的机器学习框架,强化学习采用不断的“交互-试错”机制[7],实现决策函数和环境的持续交互,从而学得完成任务的最优策略,契合了人类提升智能的行为决策方式[8-13]。针对传统神经网络的隐层层数和隐层节点数根据经验选择导致泛化性能和非线性逼近能力不可控的问题,结合强化学习在行为决策方面的优势,在长短时记忆神经网络的基础上,笔者提出了强化学习三态组合长短时记忆神经网络。RL-3S-LSTMNN具有较好的泛化性能、非线性逼近能力和收敛速率。
利用所提出的RL-3S-LSTMNN的优势,笔者提出了基于RL-3S-LSTMNN的状态预测方法。将该方法用于旋转机械状态退化趋势预测,可获得较理想的预测精度和较快的计算效率。
1 强化学习三态组合长短时记忆神经网络
1.1 RL-3S-LSTMNN的理论模型
RL-3S-LSTMNN模型通过构造单调趋势识别器将时序数据分为3个趋势单元(平稳、下降和上升),再采用强化学习分别为每个趋势单元选取一个隐层层数和隐层节点数与其变化规律相适应的长短时记忆神经网络。该模型如图1所示。

图1 RL-3S-LSTMNN模型Fig.1 Model of RL-3S-LSTMNN
RL-3S-LSTMNN模型具体的思路如下:
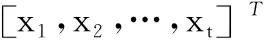
x=ht+b
(1)
平方拟合误差为
(2)
为了求出最优拟合方程,依据微积分求极值原理,需满足以下条件

(3)

其中:λ<0且μ>0。以上就是最小二乘回归单调趋势识别器的构造过程。
将上述3种趋势状态作为强化学习的环境状态,决策函数依据当前的趋势状态,从动作集a里选取执行一个动作,动作集a如表1所示。
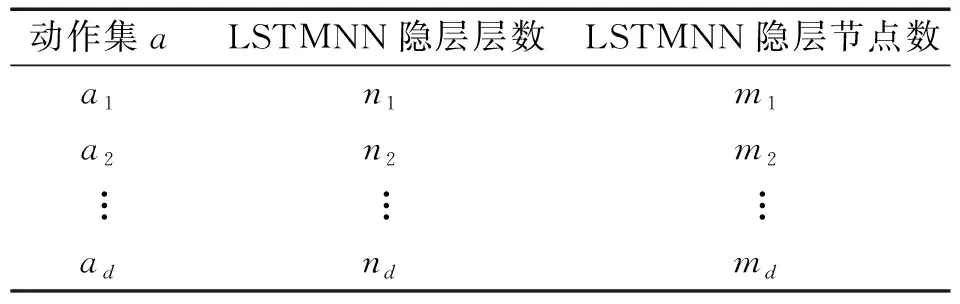
表1 动作集aTab.1 Action set a
在选取动作的过程中,采用由状态集s与动作集a构成的Q表替代折扣累积奖励期望值,如表2所示。

表2 Q表Tab.2 Q table
根据Q表(Q表用于保存奖励,Q值即动作选择的依据,每次执行动作获得的奖励再反馈更新Q值,经过多次动作执行后,Q表里的Q值会趋于稳定,因此稳定的Q值储存了学习获得的经验),利用决策函数为每个状态选取一个相对应的动作,决策函数的表达式为
(4)
其中:a*(si)∈a1,a2,…,ad,i∈1,2,3表示在状态si下决策函数选取的动作。
得到状态si下相应的动作a*(si)后,再根据a*(si)表示的网络隐层层数和隐层节点数对一个LSTMNN进行设置,就得到一个与时序xt(即趋势状态si)对应的长短时神经网络,记作i-LSTMNN。
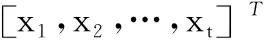
(5)
(6)
(7)
根据矩阵运算法则可知,隐层节点数和输入向量维数共同决定权值和活性值维度,因此式中各门的权值和活性值的维度为t×m。为了简化网络的更新过程,将各偏置量简略,因此只需对权值与活性值进行更新。
(8)
(9)
(10)
(11)

1.2 RL-3S-LSTMNN的学习算法
RL-3S-LSTMNN的学习过程划分为两步:①强化学习Q表的更新;②与每个趋势状态相对应的最终i-LSTMNN权值和活性值的更新。
1.2.1 强化学习Q表的更新

(12)
在状态si下,结合输出误差,选取动作a得到的奖励r由下式计算
(13)
其中:e为自然指数。
显然r∈(0,1)且与输出误差成负相关(即输出误差越大,奖励值越小)。
再根据贝尔曼方程和奖励值更新Q表中状态si下选取动作的Q值
q(si,a)′=
(14)


1.2.2 最终i-LSTMNN权值和活性值的更新
这里通过随机梯度下降法来更新权值和活性值,如果最终i-LSTMNN隐层层数为1,由式(5~9)、式(12)和链式求导法可得到各权值和活性值的梯度,再根据如下公式进行更新
(15)
其中:W′和U′为更新后的权值和活性值;ψ为学习率。

2 基于RL-3S-LSTMNN的状态退化趋势预测方法
2.1 基于RL-3S-LSTMNN的状态退化趋势预测方法实现过程
如图2所示,基于RL-3S-LSTMNN的旋转机械状态退化趋势预测方法的实现过程如下。

图2 基于RL-3S-LSTMNN的状态退化预测方法实现过程Fig.2 Implementation of the proposed state degradation trend prediction method based on RL-3S-LSTMNN
1) 使用奇异谱熵[14]对旋转机械全寿命振动数据进行特征提取。
2) 通过滑动平均方法对奇异谱熵进行降噪处理,并将降噪后的奇异谱熵作为旋转机械状态退化特征。
3) 将此特征输入到RL-3S-LSTMNN进行训练。由文中1.2节的学习过程可知,RL-3S-LSTMNN的训练过程分为:采用单调趋势识别器判别输入序列的趋势、训练强化学习和训练最终与趋势状态相对应的i-LSTMNN。
4) 通过训练好的与趋势状态对应的i-LSTMNN来预测旋转机械状态退化趋势。
RL-3S-LSTMNN的训练过程如下:取一段奇异谱熵序列[xb,xb+1,…,xb+(l+1)t-1]作为训练样本,然后对此序列进行分解
T1=[xb,xb+1,…,xb+t-1]⟹
T2=[xb+t,xb+t+1,…,xb+2t-1]⟹
⋮
Tl=[xb+(l-1)t,xb+(l-1)t+1,…,xb+lt-1]⟹
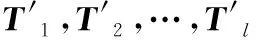
把样本依次输入RL-3S-LSTMNN中,根据1.2节Q表的更新过程实现强化学习的训练。首先,采用单调趋势识别器判别l组训练输入样本的趋势状态;然后,根据强化学习最终更新的Q表选取最优动作,分别为3种趋势状态选择最终对应的i-LSTMNN(1-LSTMNN、2-LSTMNN、3-LSTMNN)。接下来,通过随机梯度下降法分别对选取的i-LSTMNN训练M次,即在每次训练之前从状态si的训练样本中随机地选取一组样本输入对应的i-LSTMNN,再根据1.2节i-LSTMNN的更新法则,完成i-LSTMNN的一次训练。重复上述训练过程M次,就完成了RL-3S-LSTMNN的完整训练过程。

2.2 奇异谱熵机理
在正常状态下,滚动轴承的振动时域信号近似为高斯分布,这时信号主要源自保持架转频和轴频,以及保持架相对轴旋转产生的微弱调制,信号频率成分简单,能量集中在少数几个频率分量中,使奇异值分解结果集中在少数几个模式上,因此信号的奇异谱熵[14]较小;随着滚动轴承出现最细微的状态退化,信号中产生了微弱的故障频率以及引起微弱的共振频率,信号能量开始分散,奇异值分解结果也随着分散,从而奇异谱熵开始增加;当出现明显的状态退化时,噪声信号的频率成分所占的比例迅速增加,能量加剧分散,使奇异谱熵增大。基于以上分析,奇异谱熵可以作为旋转机械的状态退化特征来描述其振动时域信号的变化趋势,即能反映旋转机械状态的退化趋势。
3 实例分析
使用Cincinnati大学实测的滚动轴承状态退化数据对所提方法进行验证[15]。图3所示为实验装置,轴承实验台的转轴上安装4个航空用轴承,这些航空轴承是Rexnord公司生产的型号为ZA-2115的双列滚子轴承,实验中轴承被施加了6 000 lbs的径向载荷,交流电机通过带传动使转轴以2 000 r / min的恒定转速旋转。采样的频率为20 kHz,采样长度为20 480,每10 min采集一次轴承的振动加速度数据,轴承持续运转直到出现故障。

图3 滚动轴承性态退化实验装置Fig.3 Test equipment of the performance degradation of rolling bearings
实验台持续运行21 560 min后,3号轴承出现内圈故障。这里采用3号轴承的振动加速度数据验证所提方法。3号轴承的全寿命振动数据有2 156组,每组20 480个数据,分别提取每一组前10 000个振动加速度数据进行矩阵重组得到维数1 000×10的矩阵并计算奇异谱熵(无量纲量),如图4(a)所示。对奇异谱熵序列执行滑动平均降噪处理得到降噪后的奇异谱熵序列,如图4(b)所示。从图4(b)可看出,从起始点到第200点的奇异谱熵快速上升,轴承处在跑合阶段;从第200~1 700点的奇异谱熵变化缓慢,奇异谱熵曲线较为平直,轴承处在运行平稳的阶段;第1 700点之后的奇异谱熵变化速率持续加快,奇异谱熵曲线开始急剧上升,轴承处在故障加剧即状态退化加剧阶段,直到失效。由于3号轴承失效是内圈故障逐步恶化造成,因此在平稳阶段的后期(即从第1 300~1 700点区间),3号轴承实际就处在早期故障阶段即初始退化阶段。将处在初始退化阶段的第1 301~1 500点(共计200个点)的奇异谱熵作为训练样本;依据第2节表述的RL-3S-LSTMNN预测过程来预测第1 501~2 156点(即最后656个点)的奇异谱熵。

图4 3号轴承的全寿命奇异谱熵Fig.4 Singular spectral entropy in the whole life of the third bearing
RL-3S-LSTMNN的参数设置如下:状态趋势识别器的临界值λ=-7×10-6,μ=7×10-6;强化学习过程训练轮数P=5、选取动作的参考值ε=[0.9,0.7,0.5,0.3,0.1];每轮训练的次数Kρ=100ερ;动作集是由可选隐层层数[1,2,3]与可选隐层节点数3~10两两组合共计24种动作组成的集合;Q表中各Q值的初始值为区间[0,1]内的随机数;Q值更新的折扣因子γ=0.001,Q值更新的调节系数α=0.1;i-LSTMNN的学习率ψ=0.001和训练次数M=2 000;训练样本组数l=49;预测回合数V=164;各回合预测次数(即输入节点数,也即样本维数)t=4;输出的节点数为1。图5为RL-3S-LSTMNN的预测结果。

图5 RL-3S-LSTMNN预测的奇异谱熵曲线Fig.5 Singular spectral entropy prediction curve obtained by RL-3S-LSTMNN
为验证笔者提出的基于RL-3S-LSTMNN的旋转机械状态退化趋势预测方法的优势,首先采用一种常用的退化特征——排列熵(无量纲量)与文中选用的奇异谱熵的预测效果进行比较,其中排列熵嵌入维数d=5,延迟时间τ=3。如图6(a)为3号轴承的全寿命过程的排列熵,对排列熵序列进行滑动平均降噪处理得到降噪后的排列熵序列,如图6(b)所示。同样地,取图6(b)第1 301~1 500点(共计200个点)作为训练样本;根据第2节阐述的RL-3S-LSTMNN预测过程来预测第1~501~2 156点(即最后656个点)的排列熵。RL-3S-LSTMNN参数设置保持不变,预测结果如图7所示。

图6 3号轴承的全寿命排列熵Fig.6 Permutation entropy in the whole life of the third bearing

图7 RL-3S-LSTMNN预测的排列熵曲线Fig.7 Permutation entropy prediction curve obtained by RL-3S-LSTMNN
由图7可知,尽管RL-3S-LSTMNN预测的排列熵曲线与实际的排列熵曲线十分接近,但如图6所示,排列熵所描述的状态退化过程没有明显区分出3个退化阶段(即平稳阶段、初始退化阶段和故障加剧阶段)。而如图4(b)所示,文中选用的奇异谱熵能较清晰地区分出个这3个退化阶段。因此,笔者选用的奇异谱熵比排列熵更能清晰反映轴承的退化趋势。
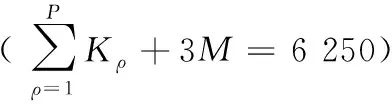

图8 LSTMNN,MK-LSSVM,GA-BPNN和ELM预测的奇异谱熵曲线Fig.8 Singular spectral entropy prediction curves obtained by LSTMNN, MK-LSSVM, GA-BPNN and ELM
为更好地评价模型的预测效果,采用纳什系数(Nash-sutcliffe efficiency coefficient,简称NSE)、均方根误差(root mean square error,简称RMSE)以及平均绝对百分比误差(mean absolute percentage error,简称MAPE)作为预测精度的评估指标,即


表3 5种状态退化趋势预测方法的预测性能对比Tab.3 The prediction performance comparison of five state degradation trend prediction methods
然后,在3号轴承原始的全寿命振动加速度信号中加入白噪声以验证奇异谱熵具有较强的容噪能力。图9(a,c,e)分别为随机抽取的加入噪声后的平稳阶段、初始退化阶段和故障加剧阶段的一组振动加速度数据的时域图,图9(b,d,f)为对应的功率谱分析结果(其中功率为无量纲量)。图10(a)为加入白噪声后的全寿命过程的奇异谱熵,图10(b)为滑动平均降噪后的奇异谱熵。RL-3S-LSTMNN对滑动降噪后的奇异谱熵的预测结果如图11所示。

图9 3号轴承加噪声后的振动加速度数据及对应的频谱分析Fig.9 Vibration acceleration data of the third bearing after adding noise and corresponding spectrum analysis

图10 3号轴承加噪声后的全寿命奇异谱熵Fig.10 Singular spectral entropy in the whole life of the third bearing after adding noise
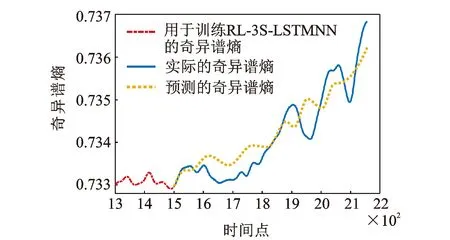
图11 加入噪声后RL-3S-LSTMNN预测的奇异谱熵曲线Fig.11 Singular spectral entropy prediction curve obtained by RL-3S-LSTMNN after adding noise
图10表明:在原始振动数据中加入背景噪声后,计算得到的奇异谱熵经过滑动降噪后,依然能较清晰地描述3号轴承所经历的跑合、平稳、初始退化和故障加剧这4个完整的退化过程,这表明奇异谱熵具有较强的噪声容纳能力。图11表明,由RL-3S-LSTMNN预测的奇异谱熵曲线与实际的奇异谱熵曲线很接近,而且与图5所示的没有加背景噪声下预测的状态退化趋势整体一致,因此RL-3S-LSTMNN具有较好的适用性和鲁棒性。
最后,再用LSTMNN,GA-BPNN,MK-LSSVM和ELM完成状态退化趋势预测所花费的计算时间(即训练时间和预测时间之和)与RL-3S-LSTMNN所花费的计算时间进行比较,结果见图12。RL-3S-LSTMNN的计算时间仅为14.782 s,LSTMNN消耗的时间为10.866 s,GA-BPNN的计算时间为35.636 s,MK-LSSVM的计算时间为26.051 s,ELM的计算时间为22.374 s。很明显,RL-3S-LSTMNN的计算时间比GA-BPNN,MK-LSSVM和ELM都短,仅比LSTMNN略长(但两者仍在同一数量级)。由上述的比较结果可知:将RL-3S-LSTMNN应用于双列滚子轴承的状态退化趋势预测,其收敛速率和计算效率比GA-BPNN,MK-LSSVM和ELM更高。

图12 5种状态退化趋势预测方法消耗时间对比结果Fig.12 The comparison results of computation time taken by five state degradation trend prediction methods
4 结束语
RL-3S-LSTMNN通过构造的单调趋势识别器判别输入序列的趋势,用不同隐层层数及隐层节点数和3种趋势状态分别表示Q表的动作和状态,依据最终更新的Q表来选择最优动作(即选取隐层层数和隐层节点数与各趋势单元最适应的长短时记忆神经网络)。所以,RL-3S-LSTMNN获得了较高的泛化性能和非线性逼近能力。在强化学习训练过程中,为明确强化学习的学习目的(即使得输出误差较小),利用输出误差构造奖励函数,可避免决策函数在Q表更新过程中盲目搜索动作,以提高RL-3S-LSTMNN的收敛速率。由于RL-3S-LSTMNN在泛化性能、非线性逼近能力、收敛速率上的优势,所提出的基于RL-3S-LSTMNN的旋转机械状态退化趋势预测方法具有较理想的预测精度和计算效率。双列滚子轴承的状态退化趋势预测实例验证了所提出方法的有效性。
