摩擦式提升机钢丝绳鲁棒纵向振动抑制*
2020-12-08朱真才丁兴亚
朱真才, 沈 刚, 丁兴亚, 汤 裕, 李 翔
(中国矿业大学机电工程学院 徐州,221116)
引 言
深井提升系统作为矿井生产的咽喉,其稳定运行状态影响着企业的生产效率和人员的安全。钢丝绳是保障提升系统安全运行的一个关键构成单元,但在实际运行过程中,钢丝绳由于重载长距离提升,自身存在一定的弹性形变,同时钢丝绳本身由于生产制造误差、钢丝绳与绳槽的磨损以及钢丝绳在摩擦滚筒上的滑动、蠕动等因素会引起钢丝绳的横向及纵向振动,加之提升容器与罐道之间的冲击以及井内的空气干扰都会使得钢丝绳的振动变得更加剧烈,致使钢丝绳承受强复变载荷,加剧其疲劳损伤程度,进而减少使用寿命,也会影响乘坐人员舒适性[1-3]。
为了抑制提升钢丝绳的振动,国内外学者已做了一定的研究。文献[4]应用Hamilton原理和有限差分法,研究了天轮轴向摆动对提升钢丝绳横向振动的影响。文献[5]研究了一类存在外界干扰和参数不确定情况的柔性结构振动抑制问题,提出了一种基于神经网络状态观测器的主动振动抑制方法。文献[6]针对钢丝绳横向振动抑制存在的外界干扰问题,设计了扰动观测器以消除边界扰动。文献[7]在钢丝绳的振动模型中引入节点应变率,并通过设计的线性二次调节控制器实现了钢丝绳的振动抑制。文献[8]针对存在外部干扰和测量误差的柔性航天器无惯性姿态控制问题,通过设计一种新的中间观测器已估计姿态和模态信息,实现了姿态稳定和振动抑制。文献[9]通过设计一种基于观测器的输出反馈控制律抑制矿用钢丝绳的轴向振动。与矿用提升机相关,关于电梯提升钢丝绳振动问题也有一定的研究[10-12]。
综上,笔者以摩擦式提升机为研究对象,考虑到提升机动力学模型的复杂性及参数不确定性,以自适应鲁棒控制理论设计提升钢丝绳振动抑制控制器,取得了较为理想的控制效果。
1 数学建模
笔者以摩擦式提升机为研究对象,为了对该系统进行动力学分析,首先需要建立系统的动力学模型。因为摩擦式提升机的4根提升钢丝绳具有类似的动力学特性,因此将模型进行简化,以单根提升钢丝绳为研究对象,该机构的简化模型如图1所示。

图1 摩擦式提升机简化模型Fig.1 Simplified model of friction hoist
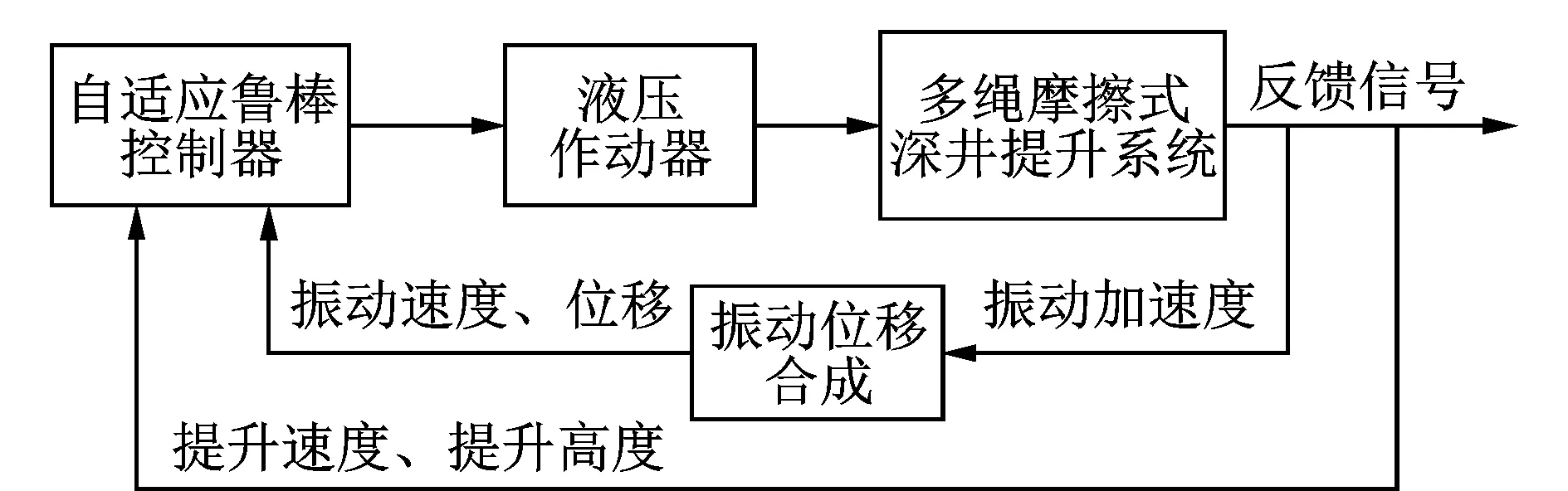
图1中天轮下安装有液压作动器。提升系统运行过程中,提升容器上安装的加速度传感器将容器的振动加速度反馈回控制系统,并计算得到容器的振动速度和振动位移。控制器即可根据实时获得的天轮端和容器端的振动位移、振动速度以及提升状态参数,求解所需的控制输入,并通过电液伺服系统完成振动位移的补偿,实现振动抑制。
假设该提升系统采用的是刚性罐道,则对提升容器振动影响较大的只有钢丝绳的纵向振动,在建模过程中,笔者将横向振动进行了忽略。在t时刻,位于垂直提升主绳空间位置x处某一质点的纵向振动位移为u(x,t),该点的动态张力P(x,t)为该点的准静态张力T(x,t)与弹性力EAε(x,t)之和,其数学表达式为
P(x,t)=T(x,t)+EAε(x,t)
(1)
其中:EA为钢丝绳抗拉刚度;ε(x,t)为钢丝绳在空间位置x处、t时刻的正应变,且ε(x,t)=ux(x,t)。
以垂直提升主绳作为研究对象,在进行系统动力学建模时先做以下假设:
1) 提升钢丝绳和尾绳均为均值钢丝绳;
2) 提升钢丝绳的形变与张力服从胡克定律;
3) 不考虑空气阻力对钢丝绳和提升容器的影响。
然后,基于Hamilton原理推导垂直提升主绳纵向振动方程。系统动能为
(2)

假设尾绳为集中于提升容器底部的集中质量,则ma的数学表达式为
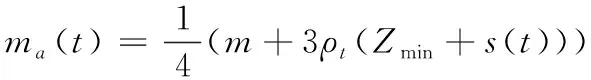
(3)
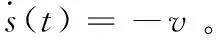
系统势能为
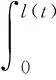
(4)
其中:T(x,t)为在t时刻垂直提升主绳空间位置x处质点的准静态张力。
T(x,t)可表示为
T(x,t)=(ma(t)+ρ(l(t)-x))g
(5)
系统虚功为
(6)
其中:c1,c2分别为提升容器和天轮处的阻尼系数;f(t)为液压作动器施加给天轮的激振力。
应用Hamilton原理

(7)
联立式(2)、式(4)和式(6),结合系统几何边界δW(0,t)=δW(l,t)=0,运用变分理论与分部积分算法,可以求得提升钢丝绳纵向振动的自由振动方程为
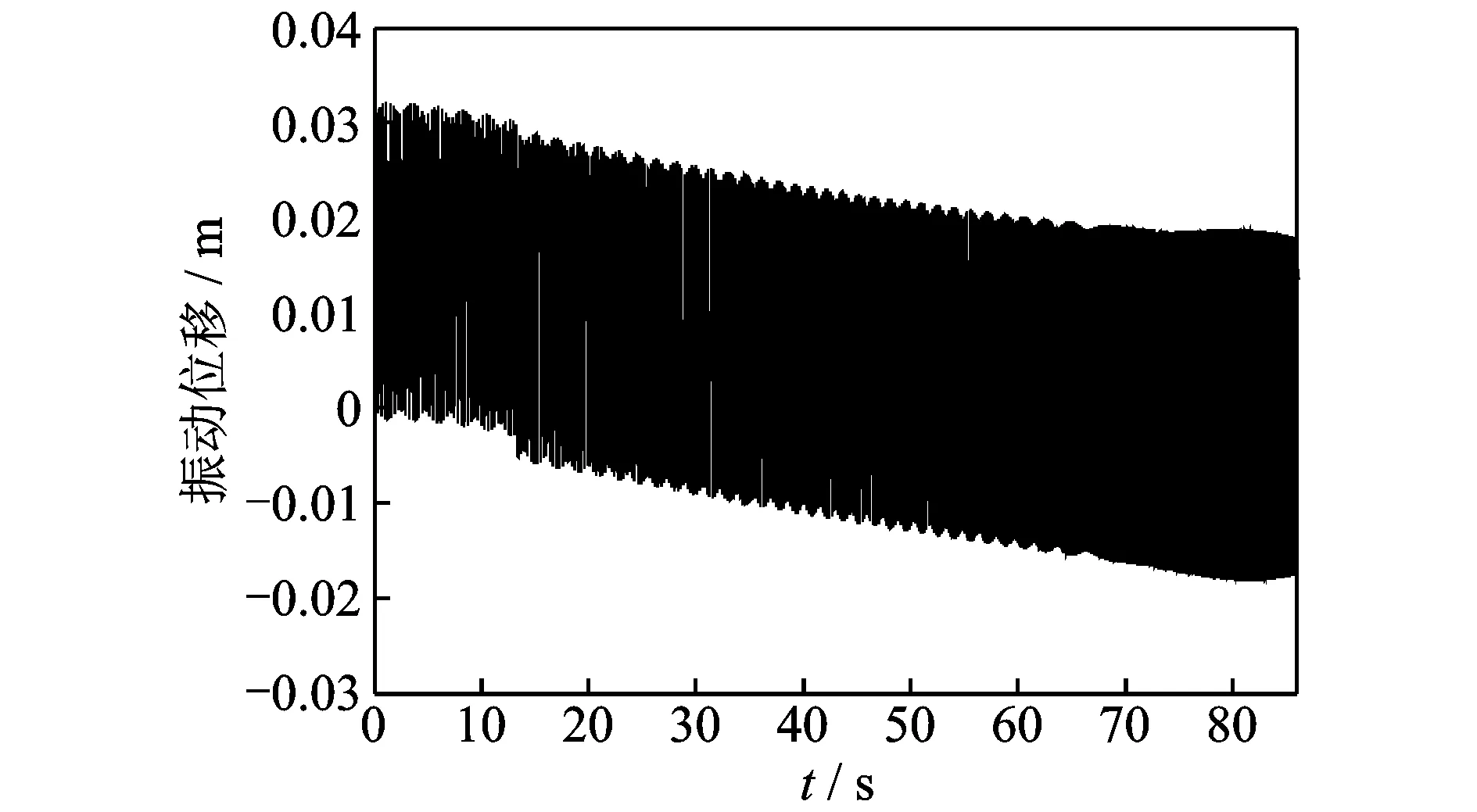
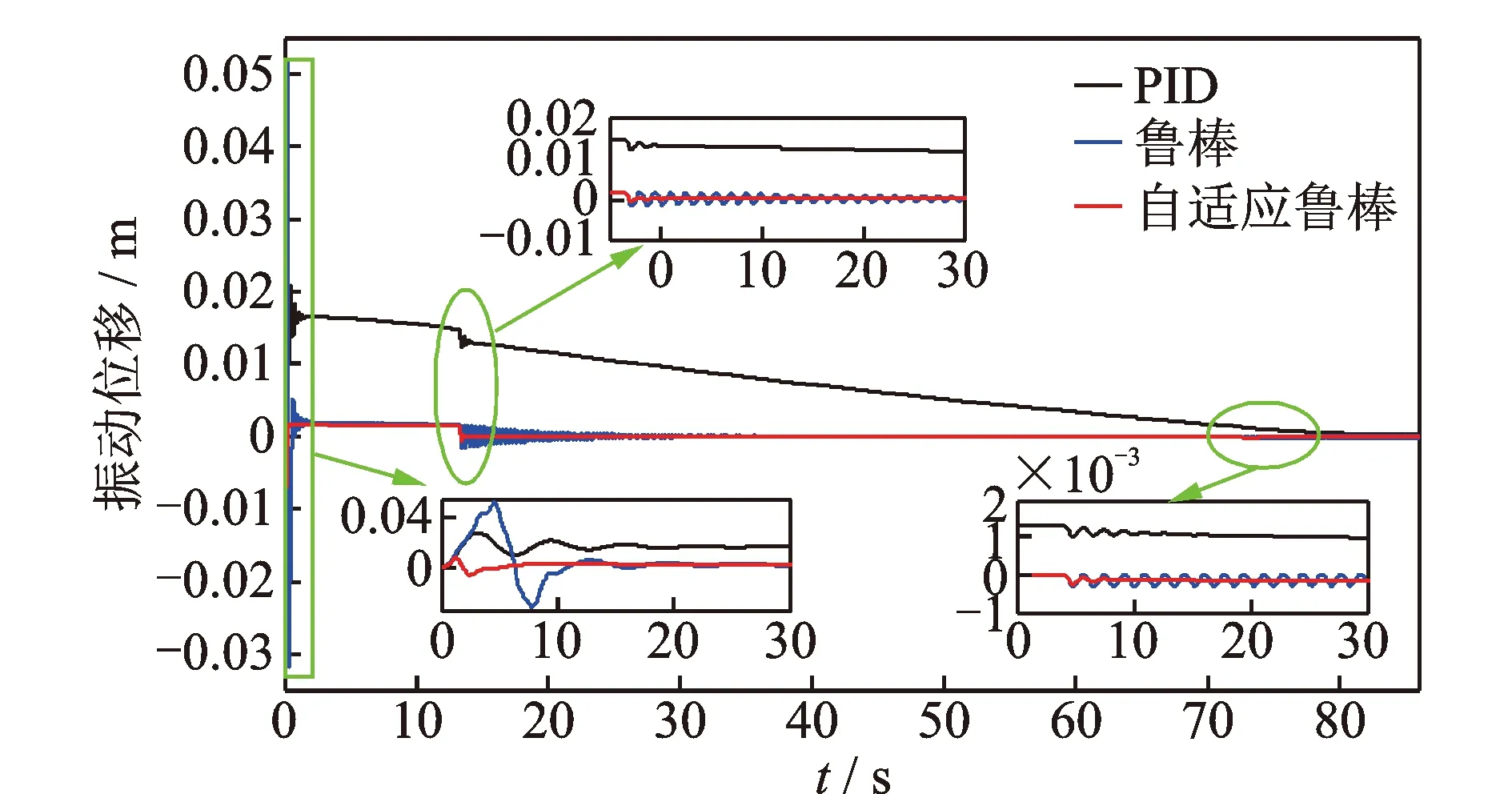
EAuxx+ρg=0 (0 (8) T-f-c2(v+ut+vux)=0 (x=0) (9) EAux+mag-c1(v+ut+vux)=0 (x=l) (10) 由式(5)可以得到 T(l,t)=mag (11) T(0,t)=(ma+ρl)g (12) Tx=-ρg (13) 将式(11)~(13)代入式(8)~(10)进行简化,可以得到 (0 (14) (15) 式(14)~(16)即为笔者研究的摩擦式提升机动力学模型,基于此进行下面的控制器设计。 图2所示为提升钢丝绳振动抑制的控制系统图。 图2 提升钢丝绳振动抑制控制原理Fig.2 Control principle of vibration suppression of hoisting wire rope 考虑系统模型参数不确定性,定义系统的未知参数 不同的移动应用类型在实现方式上对应着不同的应用开发技术栈,主要包括传统模式、Bridge模式和寄生模式等3种。 φ=[c1c2ma] (17) 则未知参数的观测值为 (18) 结合系统的动能和势能,定义Lyapunov函数为 (19) 同时 由式(19)可以发现,当满足条件α>2βl时,V(t)是正定的。为了进行控制律的设计,首先对式(19)求导,同时结合系统状态方程(14)~(16)可以得到 (v+ut+vux)((ma+ρl)g-f)|x=0- c2(v+ut+vux)2|x=0 (21) 由式(5)可得 (22) 同时,基于分布积分法,可以得到 由此可以得到 (25) 其中 (27) 将控制律式(26)代入式(25),可以得到 (28) 其中 (29) 定义参数自适应律为 (30) 其中:λr为正常数。 将自适应律式(29)代入式(27),可以得到 (31) (32) 由此可以证明,所设计的控制律能够保证系统的稳定性。 为了验证所提算法的有效性,运用Matlab仿真软件对所提的振动抑制算法进行仿真研究,并采用传统的PID算法进行对比验证。PID控制律为 f=(z1u+z2(ut+vux))|x=0 (33) 仿真中摩擦式提升系统的物理参数如表1所示。 表1 摩擦式提升系统仿真物理参数Tab.1 Simulated physical parameters of frictional lifting system 提升系统的提升高度与提升速度曲线如图3、图4所示。当系统处于开环状态下运行时,提升容器的纵向振动位移如图5所示。 图3 提升系统的提升高度曲线Fig.3 Lifting height curve of the lifting system 图4 提升系统提升速度曲线Fig.4 Speed curve of the lifting system 图5 无控制器时提升容器处的纵向振动Fig.5 Longitudinal vibration at the lifting container without controller 由图可以看出:提升过程中,提升容器有较大的纵向振动;同时随着提升高度的增加,即提升钢丝绳的悬垂长度逐渐减小,提升容器的振动位移偏移量也在逐渐减小,而振动频率逐渐增加。在运行的第13.3s和第72.7s,容器的振动位移由于提升加速度的变化而出现了突变。这些现象都说明了提升系统在运行过程中,提升容器和提升钢丝绳存在较为明显的振动,影响系统的安全性和舒适性。 接着,分别给系统施加传统PID控制器、鲁棒控制器和自适应鲁棒控制器。在仿真中,为了验证算法对未知系统参数下的控制效果,采用提升容器处阻尼系数和天轮处阻尼系数均为0.3,单根钢丝绳容器及载物质量为9 500 kg。 传统PID控制器和笔者设计的自适应鲁棒控制器的控制参数如表2所示。 表2 摩擦式提升系统振动抑制控制参数Tab.2 Control parameters for vibration suppression of the frictional hoisting system 当系统处于闭环状态下运行时,即给系统分别施加PID控制器、鲁棒控制器和自适应鲁棒控制器时,提升容器的纵向振动位移如图6所示。图7所示为自适应鲁棒控制器的控制输入曲线。由图6可以看出,传统的PID控制器对容器的纵向振动已有较为明显的补偿和抑制,但是由于其没有考虑提升钢丝绳的弹性形变,容器的振动位移在开始阶段还是有较大的偏移。当采用鲁棒控制器时,由于存在系统参数不一致的问题,使得系统在加速度突变点具有较强烈的高频振动,且收敛较慢。采用笔者设计的自适应鲁棒控制器时,容器的振动位移偏移可以得到很好的补偿,同时在加速度变化的时间点,自适应鲁棒控制器也比PID控制器和鲁棒控制器均有更快的收敛速度,总体控制效果最好。钢丝绳载重观测误差及阻尼观测值如图8所示。 图6 不同控制策略下提升容器处的纵向振动Fig.6 Longitudinal vibration at the lifting container under different control strategies 图7 自适应鲁棒控制策略控制输入曲线Fig.7 Control input curve for adaptive robust control strategy 图8 不确定参数观测值及观测误差Fig.8 Uncertain parameter observations and observation errors 本研究针对深井提升系统钢丝绳纵向振动问题,基于Lyapunov理论,提出了一种鲁棒控制策略。通过对比仿真,验证了所提算法相较于传统PID算法能更好地补偿振动偏移以及具有更快速的收敛性,整体效果良好。
2 振动抑制控制器设计

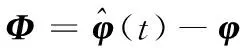

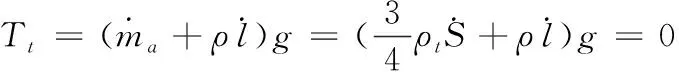
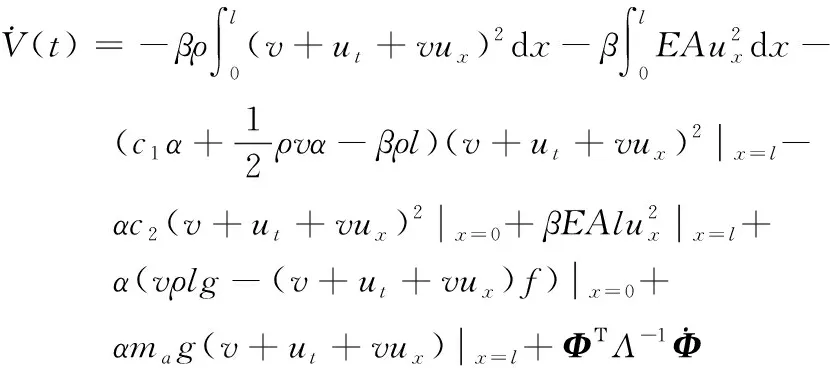
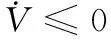



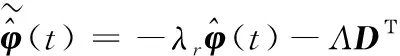



3 振动抑制仿真研究






4 结束语
